Модификация метода сопоставления размытых изображений

Создание панорамы, определение положения камеры, слежение за объектом на видео, стабилизация видео – всё это задачи, основанные на методах сопоставления изображений [1, 2], которые, в свою очередь, основаны на способах выявления особых точек [3]. Основной проблемой, с которой сталкиваются существующие способы выявления особых точек, является зашумлённость изображений: низкое разрешение, размытость, зернистость и т.д. [4]. Распространённым подходом борьбы с шумом является применение алгоритмов для их фильтрации: восстановление резкости [5], медианная фильтрация [6] и фильтрация особых точек [7].

Ранее нами был представлен метод сопоставления размытых изображений, основанный на технологии выявления особых точек на размытых изображениях (BIM), работающий лучше существующих аналогов (Harris, FREAK и SURF) [8]. Однако были выявлены некоторые недостатки метода. В данной статье представлена модифицированная версия этого метода, лишённая выявленных ранее недостатков.

1.    Описание модификаций

В соответствии с представленной ранее технологией была разработана программная реализация на языке Python с использованием библиотеки OpenCV [9] и несколькими модификациями модуля детектирования особых точек. Для получения особых точек использовались методы выделения и сравнения контуров.

Базовый алгоритм состоит из 3 этапов:

• 1.    Предварительная обработка, которая заключается в последовательном применении операций: обесцвечивания (1.1) [10], размытия по Гауссу (1.2) [10], пороговой обработки (1.3) [10] и детектирования границ Canny (1.4) [11].

• 2.    Выявление особых точек. Полученные границы аппроксимируются четырёхугольниками (2.1). Полученные четырёхугольники сравниваются между собой по площади, ширине и высоте (2.2). Выявленные пары четырёхугольников (достаточно близкие по своим параметрам, чтобы считаться равными) используются для формирования пар особых точек.

• 3.    По полученным парам особых точек с использованием алгоритма RANSAC [7] формируется проективное преобразование (3.1). Результат проективного преобразования одного изображения сопоставляется с другим изображением.

Во время проведения экспериментальных исследований с использованием базового метода было выявлено несколько недостатков: во-первых, количество выявляемых особых точек зависит от значений параметров предварительной обработки; во-вторых, далеко не для всех значений параметров предварительной обработки выявлялось необходимое для построения матрицы проективного преобразования количество точек [8]. Для устранения указанных недостатков возникла необходимость в модификации метода, целью которой являлось повышение относительного количества информативных пар выявляемых особых точек. Информативными парами называются пары особых точек, выбранные алгоритмом RANSAC для формирования проективного преобразования.

Во-первых, в рамках 2-го этапа, вместо описывания четырёхугольниками (2.1), получаемые после предварительной обработки контуры аппроксимировались многоугольниками с использованием алгоритма поиска ключевых точек контура Teh-Chin (2.1а) [12, 13]. На рис. 1 приведён пример аппроксимации контура с использованием четырёхугольника и многоугольника.

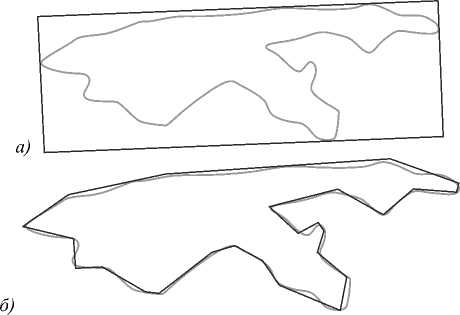
Рис. 1. Пример аппроксимации контура: четырёхугольник (а), многоугольник (б)

Поскольку изменился вид аппроксимирующей фигуры, этап 2.2 (сравнение фигур) также был модифицирован. Для сравнения пары многоугольников используются два критерия (2.2а):

I m ( A, B ) =

max i = 1..7

| m A - m B|

где m A = sign( h A ) ■ log h^A и h A - значение момента Hu [14, 15] для многоугольника A ;

I p ( A , B ) =

P A — P b

P a + P b

где P A и P B – значения периметра многоугольников A и B .

Два многоугольника называются равными, если выполняются условия I m < 0,15 и I p <0,1 (значения подобраны эмпирически). Первое условие позволяет выбирать одинаковые многоугольники, но оно инвариантно к повороту и масштабированию. Добавление второго условия позволяет гарантировать, что многоугольники получены в близком масштабе. Совместное использование обоих условий позволяет настраивать этап выявления особых точек в соответствии с решаемой задачей сопоставления.

Во-вторых, добавлены два подэтапа: подэтап фильтрации многоугольников на основе критерия I m > 0,04 в рамках обработки одного изображения (2.2а) (применение этого фильтра повышает качество отбираемых особых точек) и подэтап фильтрации особых точек на основе значения минимального расстояния между особыми точками, применяемый перед вычислением проективного преобразования (3.0а) (применение этого фильтра позволяет вычислять проективное преобразование с большей точностью). Необходимость фильтра особых точек обусловлена особенностями предлагаемых модификаций метода, а именно: поскольку для поиска проективного преобразования необходимы четыре пары особых точек, а особенности метода допускают, что точки могут быть получены от одного объекта, но при разных параметрах предварительной обработки, то для исключения случаев, когда множество особых точек располагается чрезвычайно близко, был добавлен этап отбора информативных особых точек, который заключается в исключении из рассмотрения таких особых точек, которые находятся слишком близко к одной из других особых точек. Схема алгоритма сопоставления представлена на рис. 2 а . На рис. 2 б представлена схема алгоритма, в соответствии с которой работает модуль определения особых точек.

2.    Описание экспериментов

Первый эксперимент . Для проведения экспериментальных исследований влияния различных видов аппроксимации контуров на работу алгоритма сопоставления число отбираемых особых точек на разных этапах работы алгоритма при анализе наборов данных разного размера на основе общедоступного набора данных [16] были подготовлены 4 набора данных (I, II, III, IV) по 2, 3, 4 и 10 изображений в каждом наборе соответственно. В рамках данного эксперимента изменялся только вид аппроксимирующей фигуры (многоугольник и четырёхугольник). Для оценки времени работы обработка повторялась по 100 раз для каждого набора данных и вида фигуры, впоследствии полученные значения усреднялись (табл. 1). Эксперимент проводился на процессоре с предварительно зафиксированной частотой работы. В табл. 2 приведено число особых точек, которое было получено на каждом из основных этапов работы алгоритма.

Табл. 1. Время работы алгоритма в зависимости от вида аппроксимации контуров

Номер набора	Четырёхугольники	Многоугольники	Ускорение
I	96,97	96,83	1,001
II	138,21	137,52	1,005
III	235,39	224,83	1,047
IV	843,60	782,14	1,079

а)

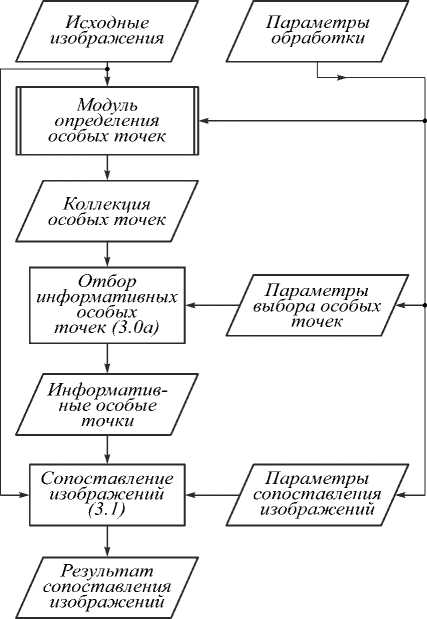
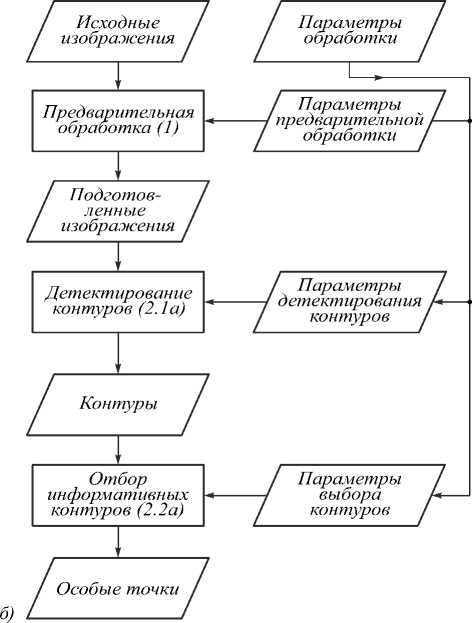
Рис. 2. Схема алгоритма сопоставления изображений: алгоритм сопоставления изображений (а), алгоритм выявления особых точек (б)

Табл. 2. Количество особых точек в зависимости от набора и вида аппроксимации на разных этапах работы алгоритма

Номер набора	Количество особых точек
	Найдено на изображениях (2.1а)	Корректных пар (2.2а)	Отфильтрованных пар (3.0а)	Выбранных RANSAC (3.1)
Четырёхугольники
I	170	85	24	17
II	672	240	39	13
III	2324	714	113	25
IV	27366	311	42	15
Многоугольники
I	102	51	17	12
II	244	107	23	14
III	814	269	75	27
IV	9268	1504	274	40

В результате анализа данных табл. 2 установлено, что использование многоугольников вместо четырёхугольников для аппроксимации контуров позволило увеличить относительное число информативных пар особых точек (в 7–8 раз для набора IV). Относительное число оценивалось как отношение числа особых точек после этапа 3.1 к числу особых точек, полученных на этапе 2.1а.

Второй эксперимент заключался в оценке качества сопоставления изображений. Качество сопоставления оценивалось на основе значения расстояния Бхатта-чариа между гистограммами исходного изображения и результата сопоставления [17]. Корректно сопоставленной считается пара изображений, значение расстояния Бхаттачариа между гистограммами изображений для которого менее 2%. Исходные данные и условия соответствуют описанным ранее в статье [8]. Первый набор содержит 4987 пар изображений без шума, второй набор содержит 3936 пар изображений с различными видами шумов. Все изображения взяты из открытых источников. В табл. 3 представлены результаты сопоставления. Доля вычислялась как отношение количества корректно сопоставленных изображений к общему числу изображений в соответствующем наборе.

Табл. 3. Доля корректно сопоставленных изображений

Алгоритм	Без шума	С шумом
SURF	59,0 %	23,6 %
Harris	94,2 %	7,6 %
FREAK	48,8 %	3,7 %
Базовый BIM	80,9 %	34,5 %
Модифицированный BIM	93,8 %	64,7 %

Таким образом, рост доли изображений, корректно сопоставленных модифицированной версией алгоритма, составил 11,9% для данных без шума и 30,2% для зашумлённых данных относительно базовой версии.

Использование многоугольников для аппроксимации контуров, хоть и является более сложной процедурой с вычислительной точки зрения, но снижает общую вычислительную сложность алгоритма за счёт того, что позволяет выполнять операции сравнения фигур точнее, что, в свою очередь, способствует увеличению доли качественных особых точек.

При проведении исследований также было замечено, что параметры обработки определяющим образом влияют на количество и качество получаемых пар особых точек. Использование одинаковых значений для большого набора изображений в некоторых случаях существенно снижает точность работы алгоритма. Это вызвано тем, что объекты, расположенные вне зоны перекрытия, оказывают существенное влияния на среднюю яркость изображений, что снижает количество вычисляемых пар особых точек.

Многоугольники по сравнению с четырёхугольниками более чувствительны к разнице яркости на изображениях. Поэтому для получения точного сопоставления при использовании аппроксимации многоугольниками необходимо особое внимание уделить выбору параметров предварительной обработки изображений. Предполагается, что использование оптимальных значений параметров предварительной обработки позволит повысить точность сопоставления изображений и снизить время работы программы за счёт снижения потребности в аугментации данных для получения точного результата сопоставления.

Заключение

Отличительными особенностями представленной модификации метода по сравнению с базовой версией являются:

– возможность одновременного использования большего числа особых точек, что способствует повышению точности получаемого результата,

– использование аппроксимации контуров многоугольниками, что позволяет выбирать небольшое число особых точек высокого качества.

Основным недостатком модифицированного метода по сравнению с базовым является увеличение числа параметров, что явилось следствием добавле- ния нескольких этапов, таких как выбор информативных контуров, фильтрация особых точек, предварительная обработка изображений, поэтому дальнейшие работы по совершенствованию метода будут направлены на разработку эффективного способа выбора параметров предварительной обработки.

Результаты исследования были получены в рамках выполнения государственного задания Минобрнауки России (Проект № 0777-2020-0017), при частичной финансовой поддержке РФФИ в рамках научного проекта № 19-29-01135.