Модификация параболического уравнения для моделирования управления адаптивными оптическими системами

Одной из главных задач адаптивной оптики можно считать компенсацию искажений волнового фронта, вызванных прохождением света через флуктуирующую среду (турбулентную атмосферу). Искажения должны быть оптимальным образом оценены и скомпенсированы, что может быть осуществлено с помощью пространственной фильтрации на основе фильтра Калмана. Вопросы построения фильтров Калмана-Бьюси для систем с распределенными параметрами рассмотрены в работах [1, 2]. В данной работе ставится задача модификации уравнения описывающего прохождение света через турбулентную атмосферу с целью приведения данного уравнения к стандартному виду, описывающему фильтр Калмана. Согласно калмановскому подходу, задача состоит в оптимальной оценке случайного процесса ф(x, t) удовлетворяющего стохастическому дифференциальному уравнению дф(x,t) r

--- ---- = Lx 'ф(x, t) + C(x, t) '^(x, t)>               (1) ∂t где Lx - линейный дифференциальный оператор, характеризующий объект управления, C(x, t)- некоторая произвольная функция, £(x, t)- возмущающее воздействие, х - пространственная координата, t -время.

В случае распространения оптического излучения через турбулентную атмосферу комплексная амплитуда оптического поля U ( z , р ), где z - координата вдоль направления распространения излучения, р - радиальный вектор, удовлетворяет уравнению параболического типа [3].

2■ i■ к 5UdZ,р) + V2U + к2 *е■ U(z,р) = 0, (2)

„₂ д ² д ² где ^{- V} 1 = тг ⁺ ту. дx ду

Уравнение (2) является линейным стохастическим дифференциальным уравнением в частных производных, содержащим в качестве коэффициента при комплексной амплитуде U (z, р) случайное поле £ (z, р)) флуктуаций диэлектрической прони- цаемости. Стохастический член £ (z, ри) U(z, р) в уравнении (2) в отличие от стохастического члена уравнения (1) имеет принципиально иную структуру, так как случайное воздействие в уравнении (1) аддитивно по отношению к функции, описывающей состояние поля, а в уравнении (2) - мультипликативно.

Постановка и решение задачи

Если уравнение (2), описывающее распространение оптического излучения, привести к виду

д U (z,р)      i z .( i ■ к _ т.(

—Д----= TTV1 U (z, р) + -;-^8 ■ U (z, р)     (3)

д z       2 ■ к                2

и формально сопоставить с уравнением (1), описывающим эволюцию стохастических динамических систем, то можно прийти к следующему заключению:

• 1)    независимой переменной, соответствующей времени t , является координата z . Аналогия z со временем проявляется не только в формальном соответствии позиционного характера, но также и выполнении принципа причинности, который применительно к уравнению (2) означает, что состояние поля U (z, р ) в точке z 1 не зависит от состояния среды в точках z > z 1 [3];

• 2)    оператору L_x соответствует дифференциальный оператор —— V 2 .

• 2 ■ к 1

Введем в рассмотрение уравнение

д U (z,р) = yir VU (z,р)- i ■ k ■ P (z, р) дz        2 ■ к

которое получается путем замены случайного поля е( r)U ( r) в уравнении (3) некоторым случайным полем р ( Г) .

Данное уравнение по своей структуре, с одной стороны, соответствует уравнению (1), а с другой стороны, адекватно уравнению (3), если случайное поле р ( Г) в каждой точке пространства будет в статистическом смысле эквивалентно случайному полю е ( r)U ( r) . Здесь r = { z , /5}.

Известно, что случайные функции (поля) можно считать эквивалентными, если их статистические моменты любого порядка совпадают, а для гауссов- ских полей достаточно равенства моментов не выше второго порядка.

В данном рассмотрении ограничимся приближенной постановкой вопроса и будем считать, что интересующие нас случайные поля ц (г) и U (Г) являются гауссовскими. Тогда уравнения (3) и (4) можно считать эквивалентными при выполнении следующих соотношений:

< ц ( г)>=< s (r)U (Г) >;                         (5)

< Ц ⁽ 1 Ч Ц ^(r 2 )>=< ^{£ ( Г ) и ( Г )} ^ £ ⁽ r 2 ) U ⁽ Л) ■.       ⁽⁶⁾

Найдем явный вид правых частей равенства, предполагая, что корреляционная функция флуктуационной составляющей диэлектрической проницаемости задана и имеет вид

< ^{£ ( Г} 1^{) £ ( Г} 2⁾ >= ^£ ( z_z 1 , Д ) ^£ ( ^z 2 , Д ) >=

= 5 ( Z 1 - z 2 ) A ( z 1 , P - P 2 )

Для дальнейших вычислений воспользуемся тем, что для гауссовского случайного поля £ ( Г) и функционала от него Ф (г, £ ( г)) справедлива формула Фуруцу-Новикова [3]

< £ ( Г ) Ф ( Г , £ ( Г )) >= j d ³ Г ' <  £ ( Г ) £ ( Г ') >

< 5 Ф ( £ ( ^Г ) ) >

5Ф где--функциональная производная.

§£

Положив в формуле Фуруцу - Новикова

Ф=и ( Г ) и принимая во внимание (7), найдем

< £ (Г) и ( Г ) >= f d² р ' А ( z , р - р ')< ^{5 U ( z} ’ ^р ) >. (9)

X Z X Z          ■        1           X > 1        1 /                    —* IX            х Z j                    5£( z, Д)

В работе [4] показано, что для поля, удовлетворяющего уравнению (3), выполняется соотношение

5U(z’Р) = ik 5(/— - /— yU(z, р'),(10)

5£ (z, р')

подстановка которого в (9) дает

< £(Г) ■ U(Г) >= ik A(z,0).(11)

Среднее поле удовлетворяет уравнению [4]

2 ik —+ V 2 + — A(z ,0) d z    ¹ 4 ⁽ )

p )>=0. (12)

Решение уравнения (12) можно представить в виде

. 2

k ² г ,      .

р )>=U o (z, р )exp - —j A ( z ,0 ) dz , 8

где g ( z , p > - поле в свободном пространстве, определяемое как решение уравнения

2 ik —+ V 2

d z    ¹

U o (z, p ) =0

При определении статистического момента второго порядка (6), как отмечено выше, будем исходить из предположения о том, что поле U( Г ) является гауссовским.

Если воспользоваться соотношением, справедливым для центрированных гауссовских случайных величин x 1 , x 2 , x 3 , x 4 :

<Х₁Х₂Х₃Х 4 >=<Х₁Х₂><Х₃Х₄>+<Х₁Х₃><Х₂Х>+

1 x 4 2 x 3 >,                                     (15)

то для второго момента можно найти

• <    ц ( Г 1)- ц ( ^Г 2 )>=< £ ( Г 1 )U ( Г 1 )>< £ ( Г 2 )U*( Г 2 )>+

+< £ (Г 1 ) £ (Г 2 )>^ (Г 1)U*( ^Г2)>+

+< £ (Г 1 ) U*( Г 2 )>< £ (Г 2 ) U( Г 1 )>.              (16)

Как следует из соотношения (11), первый член выражения (16) имеет вид

• <    £ ( Г 1 )U( Г 1 )>< £ ( Г 2 )U( Г 2 )>=< k- A(z 1 ,0)*

*A(z 2 ,0)xU(z 1 , /5 1 )>2, /52 )>.              (17)

Второй член выражения (16), вследствие дельта-корелированности по координате z первого сомножителя, можно представить в форме

• < £ (Г) £ (r 2 )>=

= 5 (z, -2)A(z, (5. - (5, )(18)

, /1         2                             1

Последний сомножитель в выражения (18) представляет собой функцию когерентности. Вводя для данной функции обозначение

= Г( z, /51, /52),(19)

можно показать [4], что она удовлетворяет уравнению

{a a2

• 2 ik — + 2 —— + — (A (z ,0)-A (z, p))[ Г (z, pv P2 ) = 0, Gz   GpGpc 2

где / 5 = Р 1 ^- Р_г, P _c = ;2 (, 5 1 ⁺ / 9 2 ) .

Решение уравнения (20) для различных физических ситуаций можно найти в работе [4].

При наблюдении звезд с помощью оптических телескопов, можно считать, что вследствие сильной удаленности звездный свет является полностью плоской когерентной волной. В данном случае уравнение (20) будет иметь решение

г( z’ р1’ р2) = expLk^J(A(z,0)-A(z,/51-/52))dz.       (21)

При определении третьего члена выражения (16) примем во внимание принцип причинности. В соответствии с данным принципом поле U( r ) не может зависеть от последующих значений 2 ( r ) и, таким образом, при z₁< z₂ поля 2 ( r ₂ ) и U( r ) будут статически независимыми, а, следовательно,

< 2 ( r ₂ )U( r j>=< 2 ( r ₂ )>гД>=0.         (22)

Аналогично в случае z₁< z₂ обращается в нуль статический момент < 2 (r_x)U *(г ₂ )>. Таким образом, для третьего члена выражения (16) находим

< 2( ^ )U *( r,) >< 2 (r2 )U( F )>= где Г(Z1,р1,р2),< U(z1,Д) >,< U*(z2,р2) > определяются соответственно выражениями (21) и (13).

Оценим интегральный вклад каждого из членов выражения (27). Введем обозначения:

да

« 1 = J ^{8 ( z}1 ^{- z} 2 ) A 5, ^{р -}Д ) ^{r ( z} p ^р ’ Д) dz ;          ⁽²⁸⁾

да 1,2

а I — A ( z 1 ,0)

0 16

A ( z 2 ,0) <  U ( z_p р 1 ) X U *( z 2 , р 2 ) >  dz .

Считая, что в турбулентной среде флуктуации показателя преломления описываются колмогоровским спектром, можно показать, что имеют место приближенные равенства [4]

A ( z , 0) - A ( z 1 , /5 1 - р , = 5,83 C „ ² ( z ) р ^5/3;          (29)

A ⁽ z ^,0) k = 0,391 C 2 ( z ) k ² L ⁵'³,                   (30)

( 0,

при z ₁ <  z ₂,

= ' <  2 ( z 1 , р ) U *( z i ,/’ ; ) ><  2 ( z 1 , / ’ ; ) >  z 2 , при z 1 = z ₂;

0,

при z 1 >  z ₂.

Воспользовавшись формулой Фуруцу-Новикова, можно найти

где р = | /5 ₁ - /5 ₂ |, С_п - структурная постоянная.

Для оценки порядков величин пренебрежем зависимостью от z структурной характеристики атмосферы Сn(z); тогда, используя (29), (30), (21), (13), найдем

< ^{2 (z} 1 ’ A U ^{( z} 1 ’ ^р 2 ) >=

a₁ = A (/5) exp

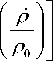
= ik A ^{( z} ’ ^{р - р} 2 ) <  ^{U ( z} 1 ’ ^рр > ^{;                (24)}

< 2 (z , P 1 )U *( z , р . ) >=

<^- k A ^{( z} ’ ^р 1 ^{- р} 2 )>< ^U * ⁽ z 1 ’ ^ Y            ⁽²⁵⁾

С учетом (24) и (25) выражение (23) принимает вид

< 2 ( rU *( r ₂ ) ><  2 (r 2 )U ( z( ) >=

0 при z1 < z2’ k2                               .                        . .                           . .

< — ^A ( z 1 ’ P 1 - P 2 ) < ^U ^ ( z 1 ’ P 1 ) >< ^U * ( z 1 ’ P 2 )

0 при z ₁ >  z ₂.

> при z 1 = z 2 ,

Сравнение выражений (26) и (18) показывает, что из-за присутствия в выражении (18) дельтафункции вкладом третьего члена выражения (16) можно пренебречь. Таким образом, имеем

< Ц ⁽ F) Ц ⁽ r D >= ^{8 (} z 1 ^- z 2 ) *

* A ⁽ z 1 ’ ^р 1 ^{- р} 2^{р Г ( z} 1 ’ ^р 1 ’ ^р 2 ) +      ^{А ( z} 1 ’ ⁰⁾ *

a ₂ = 2 A (0)exp

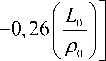
/          2   2 X -5/3

где р ₀ = ( 1,46 k C_Kz )    - радиус когерентности [4].

Численные оценки выражений (31) и (32) показывают, что при наблюдении через атмосферу для внешнего масштаба турбулентности L₀ и радиуса когерентности р ₀ справедливо L₀>> p ₀, и, таким образом, в существенной для корреляции области р<р ₀ выполняется соотношение a₁>>a₂, что позволяет пренебречь в (27) вторым членом и считать

< Ц ( Ю д ( F ) >= 8 ( ^z 1 ^{- z} 2 ) A ( ^z 1 , / 5 1 ^- / ^р 2 ) Г ( ^z , / ^/ 1 , / ^/ 2 ) ⁽³³⁾

Произведем вычисления для модельного представления турбулентной атмосферы с помощью колмогоровского спектра. В результате распространение оптического поля в турбулентной атмосфере в рамках сделанных выше предположений может быть описано с помощью уравнения (4), стохастический член которого удовлетворяет условиям:

1 k ,      .        1    k2 zz ,      .1

< Ц( r )>=у A (z ,0) exp I -—J A (z ,0) dz I

4             \   8 0)

A ( z 2 ,0) <  U ( z 1 , / 1 ) ><  U * ( z 2 , р ₂ ) > ,             (27)

< ц ( F ) Ц ( ^p ) >= ⁸ ( ^z 1 ^{- z} 2 ) • A ( ^z ’/ 5 ) *

r k ² z, ^

*exP l-тК A ( ² ,0 ) - A ( z , P ) dz ) |             (35)

V 4 0                        )

где функции A(z,0) и A(z, /5) для колмогоровского спектра флуктуаций диэлектрической проницаемости определяются соотношениями (31) и (32).

Заключение

В работе предложен метод модификации параболического уравнения, описывающего распространение оптического излучения через турбулентную атмосферу, позволяющий привести данное уравнение к уравнению описывающему фильтр Калмана-Бьюси на основе соображений приближенной стохастической эквивалентности.

Данный подход позволяет использовать аппарат фильтрации Калмана-Бьюси для управления адаптивными оптическими системами наблюдения.