Модификация схемы разделения данных Асмута-Блума с применением метода фрактальной геометрии

Хранение личной информации является важной составляющей жизни современного человека. С развитием облачных технологий для удаленного хранения данных, а также сетей для их передачи возрастает необходимость применения криптографических и некриптографических алгоритмов. Для надежного хранения информации и обеспечения распределенного доступа к ресурсам применяются схемы с разделением информации на части. В таких схемах получить доступ к ней можно, только собрав все ее части. В случае когда количество долей, достаточных для восстановления информации, отличается от общего количества частей, то применяются пороговые схемы разделения данных (СРД). Основоположниками порогового разделения данных являются А. Шамир [9] и Дж. Блэкли [10]. Позже были предложены схемы разделения данных, основанные на Китайской теореме об остатках (КТО), такие как схема Асмута-Блума [8] и схема Минь-отта [11].

Основные критерии СРД – это совершенность, идеальность и вычислительная сложность. СРД, основанные на КТО, имеют меньшую вычислительную сложность по сравнению с другими схемами. Среди схем, основанных на КТО, совершенной и идеальной является схема Асмута-Блума [8]. СРД имеют также свои недостатки: они подвергаются как внутренним, так и внешним атакам [1]. Среди СРД, основанных на КТО, выявляется один общий недостаток – если данные меньше основания СОК, то они остаются неизменными, а в противном случае они меняют свой порядок.

На рис. 1 показано, как исходный синусоидальный сигнал (см. рис. 1 а ) подвергается модулярному делению по основанию 200 (см. рис. 1 б ) и по основанию 100 (см. рис. 1 в ). Из рис. 1 видно, что часть сигнала остается неизменной, а другая часть меняет свой порядок, но не изменяет форму. Например, применив СОК на изображении, часть его будет неизменна либо будут видны его «тени».

Введение в СОК. Схема разделения данных Асмута-Блума и ее модификация

Напомним, что СОК относится к непозиционным системам счисления, числа в которой представляются в базисе взаимнопростых чисел, называемых модулями для . Произведение всех модулей СОК           называется ди намическим диапазоном системы. В диапазоне любое целое число может быть представлено единственным образом в СОК в виде вектора               где                       .

Из вышесказанного можно сделать вывод, что для порогового разделения данных предпочтительнее использовать СРД Асмута-Блума, но необходимо применять дополнительные кодирующие преобразования. В схеме разделения данных Асмута-Блума разделение данных происходит по формуле где M'=M + qr, qr – аддитивное смещение, которое добавляет шум в сигнал.

Так как пороговые схемы разделения данных подвергаются различным типам атак, например злоумышленник, прослушав линии связи, может восстановить информацию, то при использовании схемы Асмута-Блума он получит только M' . Для полного восстановления информации необходимо произвести вычитание M =M'-qr где qr - постоянная константа в диапазоне [O;^-^-^-...-^-!]. Для увеличения крипто- графических свойств константа qr должна изменяться. Величина ^ выбирается из условий q> P, где Р – динамический диапазон СОК и q>pv>P1 >...>pn, поэтому q величина постоянная. Значение r выбирается как случайное число из диапазона

q.P\- Рг' PV-- Pk _t q

В статье предлагается подход к использованию фрактальных итерационных функций в качестве кодирующей функции. Данный подход отличается от обычных методов кодирова-

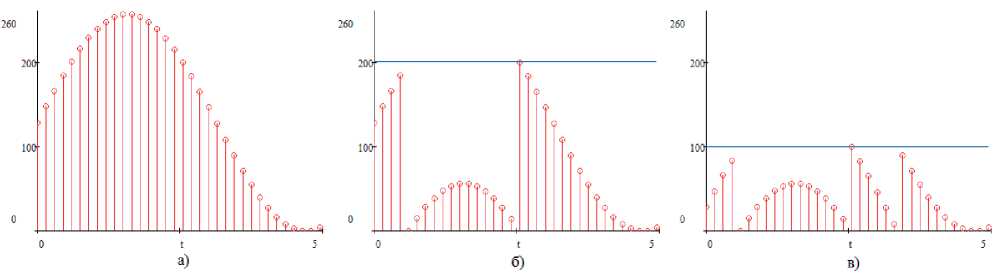
Рис. 1. Представление сигнала в СОК:

а ) исходный сигнал, б ) сигнал по модулю 200, в ) сигнал по модулю 100

ния тем, что фрактальная последовательность используется в качестве сложной кодирующей функции [3]. При этом описание этой функции, достаточное для построения, является набором вещественных чисел, которые задают начальные условия итерационного процесса построения фрактальной последовательности [4]. Этот подход является вариантом гаммирования – процесса «наложения» гамма-последовательности на открытые данные, где в качестве гамма-последовательности используется фрактальная последовательность.

Основной проблемой средств защиты информации является порождение случайных последовательностей бит. Генераторы случайных последовательностей, используемые для общих целей, являются псевдослучайными генераторами [2]. Идея применения фракталов как псевдослучайных последовательностей исходит из предположения возможности описания поведения физических и природных систем с помощью фракталов [5].

Фракталы относятся к множествам с крайне нерегулярной разветвленной или изрезанной структурой. Теория фракталов рассматривает дробные меры вместо целочисленных и базируется на количественных показателях в виде дробных размерностей и соответствующих сигнатур. Фракталы характеризуют как топологию объектов, так и эволюцию динамических систем и связаны с их свойствами. Теория фракталов и нелинейность составляют геометрию хаоса. По своему содержанию контуры всех природных объектов суть динамические процессы, внезапно застывшие в физических формах и объединяющие в себе устойчивость и хаос [6].

Таким образом, применение «генераторов шума», основанных на фракталах, дает преимущество над традиционными системами псевдослучайных последовательностей. Другим достоинством генератора псевдослучайных чисел, основанного на фракталах, является то, что он имеет бесконечное количество состояний ЭВМ в отличие от классических генераторов псевдослучайных чисел.

В статье для построения фрактала применено множество Мандельброта. Множество Мандельброта является одним из самых известных фракталов, в том числе за пределами математики, благодаря своим цветным визуализациям. Его фрагменты не строго подобны исходному множеству, но при многократном увеличении определенные части все больше похожи друг на друга. Множество Мандельброта – это множество таких точек с на комплексной плоскости, для которых итерационная последовательность при ^o — ^ является ограниченной.

Последовательность может быть раскрыта для каждой точки с на комплексной плоскости следующим образом [7]:

с = x + i у ; z₀ = 0;

з                      .                      2

z_v = Zq + с = х + i у; z₃ = z₂ + с;

• z₂ = z² + с = (х + iуУ + x + i у =

• - х² - у² + х + (2ху + y)i.

На рис. 2 слева представлен классический фрактал множества Мандельброта. Визуально внутри множества Мандельброта можно выделить бесконечное число элементарных фигур, причем самая большая в центре представляет собой кардиоиду. Пример увеличения множества фрактала представлен на рис. 2 справа.

Таким образом, применив фрактал в качестве случайной величины r , получим зашумленные части изображения. Рассмотрим алгоритм разделения информации на части с применим фрактала ее восстановления.

Изображение на ЭВМ имеет вид матрицы пикселей размерностью т х п . В каждом ее элементе хранятся значения глубины цветов в палитре RGB (Red, Green, Blue) в диапазоне [0;255]. Опера-

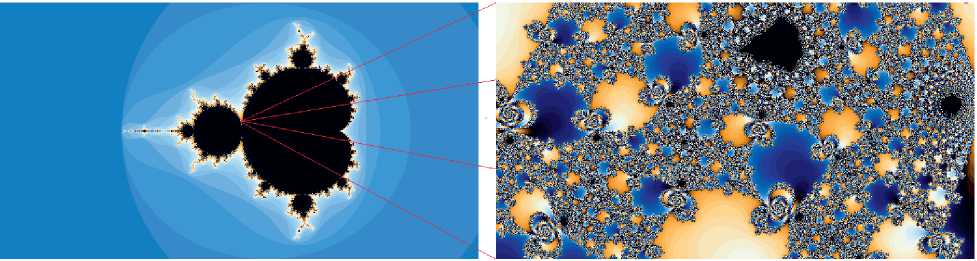
Рис. 2. Увеличение фрактала, соответствующего множеству Мандельброта

торами / и F_xv , – где О <  х < т и 0 <  у < т, обозначим матрицу исходного изображения и матрицу изображения фрактала, соответственно.

Таким образом алгоритм состоит из следующих действий.

• 1.    Выбирается ряд чисел q,p_x,p₂,...,p_n.

• 2.    Вычисляется 1_х,;=т_х.у+чг_х,-

• 3.    Вычисляются части данных ^ах^, = Л./^modА-

• 4.    Выполняется обратное преобразование из СОК в ПСС:

• 5.    Вычисляется k.=iy_;-qF_x._y.

кУ = <ах,У1 В\ + ах.у, В2 + ■ ■ ■ + ах,у„ В„ ) mod Р •

Схема разделения данных с применения фрактала представлена на рис. 3.

Применив для взлома метод «грубой силы», необходимо для каждой точки изображения перебрать все возможные комбинации. При использовании фрактала разрядностью 8 бит количество комбинаций N = 2^п Y Y ху , где .X, у – разрешение изображения; n – глубина цвета изображения. Также достоинством данного метода

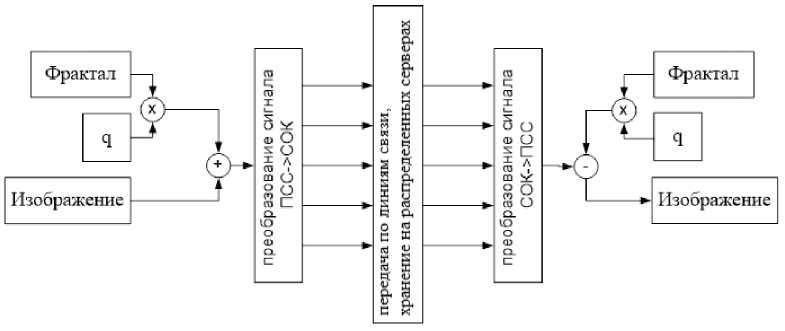
Рис. 3. Схема разделения изображения

является отсутствие необходимости хранить изображение фрактала или сгенерированные случайные числа, поскольку при восстановлении, зная схему раскраски фрактала и порядок его уравнения, числа могут быть сгенерированы заново.

Численный метод разделения информации с применением модифицированной схемы разделения данных Асмута-Блума

Для порогового разделения данных модифицированным методом Асмута-Блума необходимы две матрицы: А – матрица данных, F – матрица псевдослучайных чисел фрактала. Для простоты вычислений представим обе матрицы размерностью 3×3.

Рис. 4. Увеличение участка изображения

Необходимо заполнить массив данных и массив фрактала числами. Так как изображение – это матрица размерами тхп ^ каждый пиксель которой представлен тремя цветами (красный, синий, зеленый), то путем увеличения рисунка (как это показано на рис. 4) и с помощью инструмента Paint можно получить значения нескольких пикселей и вычислить среднее арифметическое цветов RGB:

	^100	50	30"
A =	20	150	70
	<40	200	80v
	^187	74	83 7
F =	81	70	251
	. 72	80	3

Для вычислений возьмем следующий ряд модулей: <7 = 257, /9, = 547 , /+=557, ^=563, p^ = 569 , p₅ = 571. Проверим условие: R = p_xp₂ Рз > qP4 Ps = 71534277 > 83499043.

Значения q,p_v,p,,p„p₄,p_s также упорядочены. Для вычисления частей данных необходимо массив F умножить на :

	'187	74 83 '
F = qF = 251	81	70 251
	V72	80   3 ,
48 059 19 018		21 33P
= 20 817 17 990		64 507 .
J 8 504 20 560		771 y

Далее необходимо поэлементно сложить значения в получившемся массиве и в массиве А :

^ = ZZ( л-l ,v=0	4„-F.A-
100 + 48059	50 + 19018  30 + 21331
20 + 20817	150 + 17990 70 + 64507
40 + 18504	200 + 20560   80 + 711
'48159	19018 2136P
= 20837	18140 64577 .
J 8544	20760 7091 y

Следующий шаг – это разделение данных, которое выполняется путем преобразования элементов массива A в СОК:

a = A_{x v} mod(/<) = A_{x v} mod(547) =

7 23 420 28" = 51 89 31 v493 521 527? b = Ax v mod(pz) = Ax v mod(557) = 457 80 1957 = 228 316 502 v173 151 407; c = ^> modCp, ) = Ax v mod(563) = 7304 439 5307 = 6 124 395 1 528 492 335 d = Ax v mod^J = Ax r mod(569) = 363 241 308 353 501 280 336 276 263 е = Axv mod(p,) = Д. v mod(571) =

'195	175	234"
281	439	54
^272	204	239v

Массивы a,b,c,d,e – это части информации, и они распространяются среди пользователей. Для восстановления данных необходимо провес- ментно вычесть произведение q F:

3    3	'-100 + 48059 -50 + 19018 -30 + 21331"		'100 50 30"
	-20 + 20817 -150 + 17990 -70 + 64507	=	20 150 70
x=l >-=0	^-40 + 18504 -200 + 20560  -80 + 711 y		v 40 200 80v

Блок-схема алгоритма разделения изображения на части приведена на рис. 5.

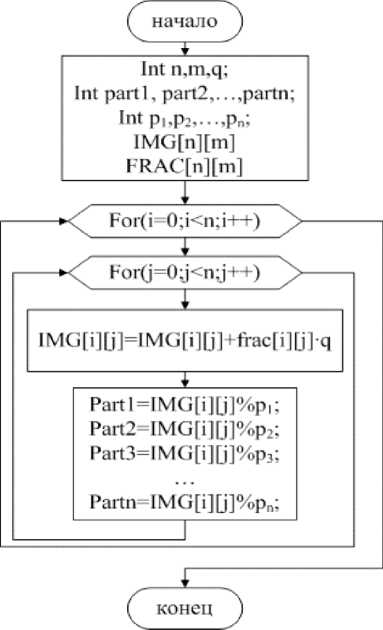
Рис. 5. Алгоритм вычисления частей данных модифицированным методом Асмута-Блума

В отличие от криптографических алгоритмов, таких как RSA, в котором вычислительная сложность равна O[log(«)2] , использование численного метода, основанного на модификации схемы Асмута-Блума с применением фрактальной геометрии, позволяет закодировать информацию, не увеличивая вычислительную сложность СРД.

ти для массивов a,b,c,d,e обратное преобразование из СОК в ПСС. Выполнив данное преобразование, получим массив

'48159 19018 21361"

A = 20837 18140 64577 .

(18544 20760 7091 J

Далее из массива данных A необходимо поэле-

Моделирование модифицированной схемы разделения данных Асмута-Блума с применением фрактальной геометрии

Рассмотрим пример реализации предложенного метода. Так как множество Мандельброта является бесконечной последовательностью, то увеличим его участок и в экспериментах будем использовать часть фрактала (см. рис. 7) для моделирования разделения изображения «Лена», показанного на рис. 7.

Применив схему, представленную на рис. 4, и алгоритм, представленный на рис. 6, а также используя набор модулей ^=547, /+=557, p^ = 563, р_л = 569, p₅ = 571, получим результаты, показанные на рис. 8.

Рис. 6. Часть фрактала, используемого при моделировании

Рис. 7. Изображение «Лена», используемое при моделировании

Другим способом искажения изображения является наложение белого шума. Применив вместо фрактала белый шум, получим результаты, показанные на рис. 9.

Визуально сравнивая изображения, представленные на рис. 8 и рис. 9, можно сделать вывод, что применение фрактальной последовательности позволит более качественно иска-

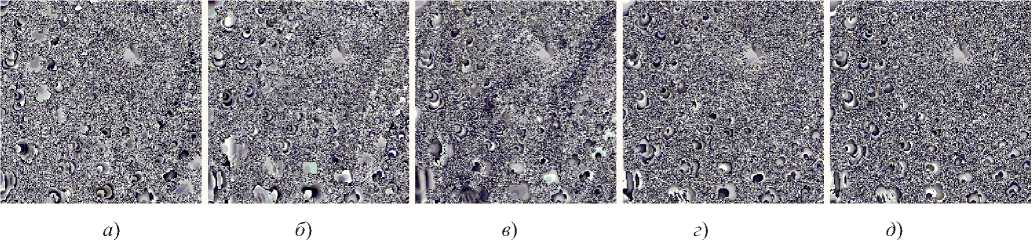
Рис. 8. Результаты работы модифицированной схемы разделения данных Асмута-Блума с применением фрактальной последовательности для набора модулей

а) 547; б) 557; в) 563; г) 569; д) 571

Рис. 9. Результаты работы модифицированной схемы разделения данных Амсута-Блума с применением белого шума для набора модулей

я) 547; б) 557; в) 563; г) 569; б) 571

зить изображение, а следовательно, более надежно его хранить и обрабатывать.

Выводы

В статье разработан модифицированный метод разделения данных Асмута-Блума с применением фрактальной геометрии, где для генерации случайного числа r применяется псевдослучайная последовательность, генерируемая фракталом. Получение информации при атаке методом «грубой силы» потребует N = 2” 2" 2” х у комбинаций. Применение численного метода на основе разработанного алгоритма позволит разделять и кодировать изображение, одновременно не повышая вычислительную сложность алгоритма.