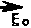Модовый состав излучения в волноводах с параболическим профилем показателя преломления, возбуждаемых локализованными источниками

МОДОВЫЙ СОСТАВ ИЗЛУЧЕНИЯ В ВОЛНОВОДАХ С ПАРАБОЛИЧЕСКИМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ, ВОЗБУЖДАЕМЫХ ЛОКАЛИЗОВАННЫМИ ИСТОЧНИКАМИ

Исследование модовой структуры поля направленных и ненаправленных излучателей, а также отклик антенн в рефракционных волноводах естественного происхождения представляет интерес в связи с проблемой формирования и управления волновыми полями в волноводах. Важной задачей при этом является нахождение начального распределения энергии между модами (фактически оно задает распределение амплитуды поля по начальному сечению волнового пучка), которые возбуждаются источниками с известной диаграммой направленности (ДН) для однородного пространства.

Данный вопрос рассматривался в ряде работ, например, [1,2], в которых найдены коэффициенты возбуждения нормальных волн однородного слоя с границами, и [3] , где в рамках приближения Вентцель-Крамерса-Бриллюэна (ВКБ) изучено возбуждение подводно-звукового канала (ПЗК) мелкого океана с учетом границ волновода и рефракции волн.

Целью данной работы является исследование начального модового состава в рефракционном волноводе, возбуждаемого локализованным источником излучения. В отличие от [1-3] здесь используется другая методика, сущность которой заключается в разложении поля по точным решениям параболического уравнения, эквивалентным когерентным состоянием [4,5]. Задача рассматривается на модели многомодового градиентного волновода с квадратичным распределением показателя преломления, которая в ряде важных случаев используется для описания естественных волноводов [б,7]. Такой подход справедлив для определения возбуждения мод с небольшими номерами (ш « М)( с которыми в основном связан перенос энергии излучения на сверхдальнее расстояние, например в ПЗК глубокого океана или ионосферных волноводных каналах (ИВК) [б, 7]. Особенно удобен при нарушении приближения ВКБ, в частности при описании лучей в окрестности оси волновода.

Рассмотрим двумерный волновод, однородный в горизонтальном направлении х и с параболическим профилем показателя преломления в вертикальном направлении z:

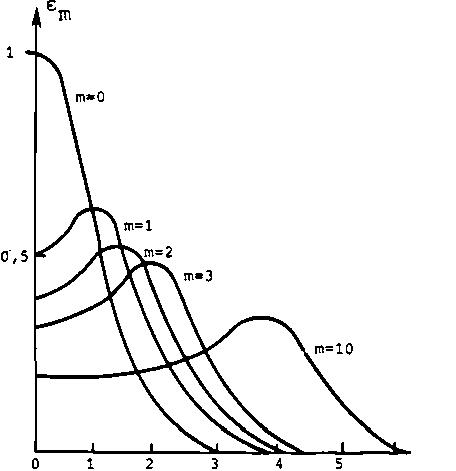
• n2 (z) = Пу -

где:

По - показатель преломления на оси волновода;

• о) - градиентный параметр среды, задающий поперечное распределение показателя преломления.

Источник излучения в таком волноводе можно считать локализованным, если его линейные размеры много меньше ширины основной моды волновода (с номером ш=0), т.е.:

• 1    « Д(г_о)                                                          (2)

Д(г0) = (кш)-^                                                          (3)

где:

к = 2п/Х;

• X - длина волны излучения.

Такие источники могут быть как точечными (1 « X) , так и протяженными (1 > X) . Причем они могут обладать определенной (и даже довольно узкой) ДН.

В однородном пространстве поле источника излучения в дальней зоне (на расстояниях L > 12/Х) представляется в виде суперпозиции однородных плоских волн [8], каждая из которых является решением скалярного уравнения Гельмгольца и распространяется по траектории геометрического луча. Однако при описании излучения источников, расположенных в рефракционном волноводе, возникает ряд особенностей.

Первая из них связана с тем, что при распространении излучения в среде с параболическим профилем показателя преломления лучи, как показано в [4], удобно описывать с помощью когерентных состояний (КС). Ука- занные КС соответствуют волновым пакетам максимально локализованным в фазовом пространстве лучей. Центр тяжести такого пакета распространяется по траектории геометрического луча, а его ширина задает область локализации луча и совпадает с шириной основной моды (3) в среде (1) . Поэтому из физических соображений представляется естественным рассматривать ДН как функцию, описывающую разложение энергии источника излучения по КС. С математической точки зрения это эквивалентно замене обычных лучей, описываемых однородными плоскими волнами, КС, т.е. неоднородными плоски ми волнами с гауссовым распределением амплитуды, представляющими собой пакет однородных плоских волн с некоторой угловой шириной.

Поскольку однородная плоская волна является математической абстракцией и в действительности ее ширина ограничена некоторым размером △ (z)_„ (например, апертурой приемника, используемого при измерении ДН), то такая замена вполне правомерна, если этот поперечный размер мал по срав нению с шириной КС (шириной основной моды волновода), т.е. при:

△ (z₀) »  (z)        (4) или со « (2k Д² (z)  )'¹.

ДН                             дн

В случае, когда ДН задана с в правую часть неравенства (4) = A/(4nnsin (Д(ф)„ц), которая дн

некоторой угловой следует поставить

точностью величину

А,ш,дн-А,2,ДН "

следует из соотношения неопределенности

(4) . При этом условие (4) эквивалентно требованию, чтобы угловая ширина

КС Дф не превосходила Вторая особенность

ДФДН : Дф « Д (ф)дн.

описания источника в таких волноводах связана с тем, что применять понятие ДН в волноводе можно лишь в тех случаях, когда на расстояниях, соответствующих дальней зоне, поперечные неоднородности среды несущественно сказываются на параметрах излучения. Таким пространственным масштабом, характеризующим расстояния, на котором изменение средних значений параметров излучения в фазовом пространстве лучей несущественно, поскольку еще не превышает их дисперсий, является длина стационарности излучения Х^, введенная в работе [9].

Например, для луча КС в среде (1) длина стационарности характеризу ет минимальное расстояние вдоль оси, на котором смещение центра пакета в фазовом пространстве лучей еще не превышает его ширины. Поэтому на расстояниях порядка длины стационарности для рассматриваемого луча среду можно считать однородной, в том смысле, что влияние неоднородности несущественно сказывается на распространении луча.

Длина стационарности луча в среде (1) определяется выражением [9]:

X® = п0/ш|а1, где:

a = (кш/2)* • (z0 + in sin Ф0/ш) ;

z0 - начальная (x=0) вертикальная координата луча;

Фо - начальный угол между лучом и осью х.

С увеличением порядкового номера луча а длина стационарности уменьшается. Поэтому если среднее число лучей, возбуждаемых в среде, равно а, где а < а^ах то длина стационарности такого пучка равна х“ . Таким образом, угловое распределение поля от локализованного источника описывается с помощью ДН- Da (здесь и далее под ДН понимается разложение поля источника по КС), если выполнено соотношение

12/Х « ^.                                                  (7)

В качестве примера укажем, что при распространении звука с частотой f = 100 Гц в ПЗК глубокого океана с ш = 10_<* м-1 источник можно считать локализованным при 1 « 600 м. Аналогичное ограничение накладывается на размеры апертуры приемника. Если источник расположен вблизи оси волновода, то из (6) следует оценка минимальной длины стационарности: Х^1 = (2k со sin2 ф )^. Так как максимальный угол наклона не превышает ср е п/12 для ПЗК (6), то X? = 4,5*10э м. Следовательно, для локализованных источников, т.е. удовлетворяющих (2), условие (7) выполняется, описание углового распределения энергии этих источников с помощью ДН правомерно .

Перейдем к анализу модового состава излучения, возбуждаемого источниками с различными ДН. Пусть в точке (х0, z0) волновода эффективной шириной h расположен локализованный источник с диаграммой направленности Da(0? ф) • Угол 0 задает направление центра ДН относительно оси волновода, а ср - угол между лучом и осью волновода. Из энергия луча распределяется между модами по закону Km I a>2 = I а I 2т ехр(-| а|2)/т!

[4J известно, что Пуассона:

виде интегрального

Тогда коэффициенты возбуждения можно представить в выражения:

/ (D (0; ф) I a I2m exp (- I a I 2) /т!) d (Ima) е =------, т                / Da(0; ср) d (Ima)

где:

I a I ² = (kco) 2) (z² + n² sin²ф/со²) ;

d(Ima) = (k/2co)n cos ф<аФ.

Полученное выражение (9) характеризует отношение энергии, захваченной в данную моду волновода, ко всей энергии, изучаемой локализованным источником.

В качестве конкретных примеров рассмотрим дипольный источник излучения с Da(0; ср) = Do cos2 (0-ф) в ненаправленный источник излучения с 0^(6; ф) = Do. Подставляя значения D^ в (9) и проводя вычисления, получим явные выражения через конечные суммы соответственно для дипольного и ненаправленного источника:

2              111

Em(e; ^o> = (Зехр(-Е0)/и) E p=0

Г(m-p+1/2)

Г(m-p+1)Г(p+1)

6=Pb<0>Vp +

+ (m-p+l/2)u 2ф2(6)Ат_р+1

(10a)

• - , ^m Г(m-p+1/2) 2d =_mo) - <=xp(-₆3)/u) Д f^^f^ e^_p'

где :

Eo = y^z0 -безразмерная вертикальная координата источника;

U = (2k Пу /2w - E2P;

Ф1 (6) = cos2 (6) / (cos2 e+1) :

Ф2(6) = cos(26)/(cos2 e+1);

p 2i-l ,   2.

J exp(-u ) A = erfu -   “—^ТГГЛ — ;

P            j=l r(j+i/2)

erf(u) = 2n 1 / exp(-t )dt - интеграл ошибки; о

r(t) - гамма функция.

Для источников, расположенных вблизи оси волновода (z0 « nQ/w), выражения (10а и 10 б) упрощаются [10]):

_ m Г(т~р+3/2) 2пг

=т<е;Е0) - (Зехр(-Еу)/ц0) в--,--™-^ е/ фне) .

.             pur         L         (11а)

+ (т-р+1/2)и02 Ф2(еу т Г(т-р+3/2) 2о =т(Е0) - (ехрС-^/МД г(т.рИ)г(р+1)

где ц0 = (к/2ш)гп0.

Зависимость коэффициентов возбуждения дипольного источника от направления ДН характеризуется первым членом в квадратных скобках выражения (11а), который не зависит от номера моды. Второй член задает поправки которые существенны в окрестности угла 6 ~5 и, вообще говоря, зависит от номера моды, а также и от остальных параметров задачи (х₀, X, ш) . Более подробно данные поправки исследованы в работе [10]. Отметим лишь, что в случае 6 - ^ коэффициенты возбуждения мод малы, режим малоэффективного возбуждения волновода. С другой стороны, изменения направления ДН (членом Ф_а(6) можно пренебречь) приводит не к перераспределению энергии между модами, а лишь к общему уменьшению энергии низших мод, захваченных в волновод. Кроме того, при фиксированном направлении ДН выражении (11а) эквивалентно (116), что позволяет далее ограничиться исследованием ненаправленного источника.

На рис. 1 представлена зависимость коэффициентов возбуждения, нормированных к величине е_о(0), от расстояния источника от оси волновода. Характерным для данных кривых является смещение максимума возбуждения моды от оси волновода при увеличении ее номера. При этом видно, что даже ненаправленный излучатель возбуждает моды неравномерно. Например, для осевого источника коэффициенты возбуждения убывают с увеличением ее номера.

Рис. 1

Таким образом, в принципе возможно селективное возбуждение отдельной группы мод ненаправленным излучателем. Для иллюстрации этого на рис. 2 представлены зависимости коэффициентов возбуждения от номера моды, нормированных к величине максимально возбуждаемой моды, при различных положениях источника от оси волновода. Из приведенной зависимости следует, что неравномерность возбуждения мод ослабляется при смещении источника от оси волновода.

В заключение приведем реккурентное соотношение, которое упрощает расчеты коэффициентов возбуждения мод ненаправленным источником:

ш-1

ет^0^

о ет-1(М /2т' т = 1,2...

2 e_d(E₀)⁺ Е р=0 ^р

В случае осевых источников оно принимает вид: е (0) = -“ ■- е . (0) . ^m      2m m-1

Таким образом, предлагаемый метод позволяет находить в явном виде коэффициенты возбуждения, которые определяют начальный модовый состав.

Наряду с приближением ВКБ, такой подход может оказаться полезным при исследовании возбуждения

естественных волноводов.