Модуляционная неустойчивость сдвиговых волн, распространяющихся в средах с дислокациями

Уравнения среды с дислокациями получаются путем варьирования калибровочноинвариантного лагранжиана Lel _ pl [5-7], состоящего из двух частей Lel _ pl = LI - pl + L', первая из которых

( I )

^Lel b pl

5 u i 5 u i

xf 5 ui

51 5t

2 (5 X i

вй

5 uk

7v

^d x k

цГ d ui

2 (5 X k

A

^в kk

в ki

цГ dut

2 (5 X k

5 uk

7V

5 x i

A

в^

в ki

5 ui

7V

^d x k

A

в ki

описывает кинетическую энергию

полных смещений и потенциальную энергию

упругих полей в среде, а вторая

L ' = ! dV

B 5в km 5вkm

B

C

2 5 1

2 ^a km ^a km

описывает кинетическую и потенциальную энергии дислокаций.

Здесь ρ – плотность материала; λ, μ – константы Ламе; B и C – константы материала, первая из которых определяет инерционные свойства дислокационного континуума (пропорциональна эффективной массе дислокаций, находящихся в единице объема), а вторая - прочностные. В работе [4] показано, что B = р 1 12 , C = ц 1 2 , где 1 1, ₂ -характерные масштабы дислокационной структуры материала, при этом 1 1 « 100 мкм -совпадает по порядку величины с размером области локализованной деформации, а

Применение общей термодинамической теории к решению проблем механики

12 » 0,1 ^ 1 мкм - определяется средним расстоянием между плоскостями скольжения, дв jm akm =еkij -x-— тензор плотности дислокации, dV- дифференциал объема.

Материал при пластической деформации предполагается несжимаемым, то есть Sp в j -в kk = 0.

Динамические уравнения упруго-пластического континуума, получаемые путем варьирования лагранжиана, имеют вид:

д 2 uz.9c

Р = д t2

д 2в,у

дв,, 2 n       .

д t

в _= ° д t2

Ранее в [12] рассматривалось распространение акустических солитонов и нелинейных периодических стационарных волн в упруго-пластической среде с дислокациями, а в данной работе рассмотрим распространение сдвиговых волн в геометрически-нелинейном континууме. Выделим из системы (1) подсистему, полагая в ней и 1 = 0 . Эта подсистема будет иметь вид д 2 и 2

Р д tт

д

д x 1

B д> - C д t^г

Ц

5^ _к д x 1

5 2 в 21

5 x 2

А в 21

ди

д к . ^д u₂

= — (Х + 2 ц ) д x 1

дx

,

1 7

Лд и 2   п

Ц        в 21

( дx1

А

= 0.

д u2

Из второго уравнения можно выразить ² , подставив полученное соотношение в д x 1

первое уравнение, продифференцировав по x 1 . Это позволит представить (2) – (3) в виде одного уравнения, которое в безразмерных переменных x = x 1 ^^B , т = tc _т ^^B ,

u v = —, u0

о в21 B в = 21 имеет вид

и 0 рР

д2р + c*2 д4р дт2 c2 дx4

/

к

1+7 '

c т 7

д4в + д4в = и 2 р с^ д 2

дx 2 дт 2   дт 4 B с 2 дx 2

+ 3^321- c.2 д2Р (дт 2

к

c _т ² д x ² ₇

в 2 + в 3

Га2р — cl ayl3 (дт2 cт2 дx2 7

,где ^c *=. C.

c т дx у

а 2

в +

Будем искать решение уравнения (4) в виде гармонической меняющимися в пространстве и времени амплитудой и фазой:

волны с медленно

в ( x , t ) = A ( s x , s t ) e i ^(ro t kx ) + к .с , где A(x,t) - комплексная амплитуда, ю и k удовлетворяют дисперсионному соотношению:

го ⁴ —

(    „2 А

^с»      2,

1 + — го k

к   с т 7

_{2     2}    c _{* 4}

— го +— 2- k = 0 . ^c т

Используя метод усреднения по “быстрым” переменным [8], от (4) перейдем к укороченному уравнению огибающей квазигармонической волны. В системе

Применение общей термодинамической теории к решению проблем механики

dto координат, движущейся с групповой скоростью (v =   ) q = v - v т, т = аt, р dk              р эволюция огибающих будет описываться нелинейным уравнением Шредингера

. дА дvгр д 2 А i--+де   дк д^2

-а| А|2 А = 0.

Здесь а =

^а о c l

где

^а 0

(

= 3 к2 to6 V

^c *   4 2 ^c *   2 4

• — 30— 2 to к + 3— 4 to к c т            c т

c 2

- 4to3

+ 2to к2

i + A

V c т J

+ 2to

6     2   24

• —    к ⁶ — 3 to ⁴ + 6    to ² к ² — 3 c * к ⁴ — 3 c * к ² + 3 to ² — 1

c т                 c т            c т         c т                J

Известно, что при определенных условиях квазигармоническая волна может оказаться неустойчивой по отношению к разбиению на отдельные волновые пакеты (модуляционная неустойчивость). Наличие в системе такой неустойчивостью д v гр определяется по критерию Лайтхилла —р а < 0 .

дк

Анализ показал, что волны, описываемые верхней дисперсионной ветвью, устойчивы. Волны, описываемые нижней дисперсионной ветвью, в интервале 0 <  к <  1,414 неустойчивы.

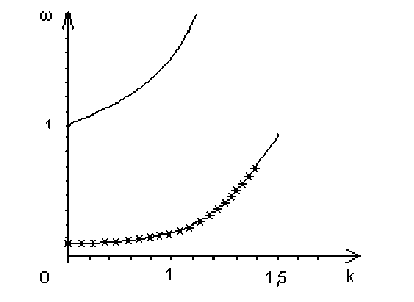
Pис.1. Диаграмма частот и волновых чисел, при которых возможна модуляционная неустойчивость

На рис. 1 изображена диаграмма, показывающая при каких частотах ω и волновых числах k возможна модуляционная неустойчивость. Область неустойчивости отмечена крестами. Расчеты производились при следующих значениях констант: μ=80 ГПа, K =Х+3/2ц=160 ГПа, р = 7,8 г/см³, 1 1 = 100 мкм, 1 2 = 1 мкм (сталь) [7].

На спектральном языке эффект самомодуляции характеризуется усилением боковых компонент в спектре модулированной волны. В эти компоненты будет перекачиваться энергия из центральной части спектра возмущения.

На рис.2 схематично изображены процесс самомодуляции квазигармонической волны и эволюция ее спектра.

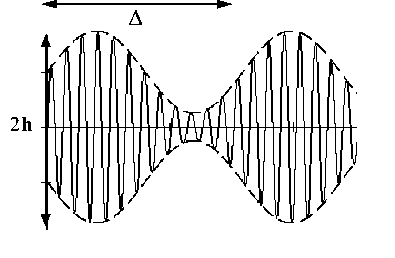
Величина области модуляционной неустойчивости сдвиговых волн зависит и от инерционных свойств дислокационного континуума.

На рис.3 показано, что область модуляционной неустойчивости увеличивается с увеличением эффективной массы дислокаций.

Применение общей термодинамической теории к решению проблем механики

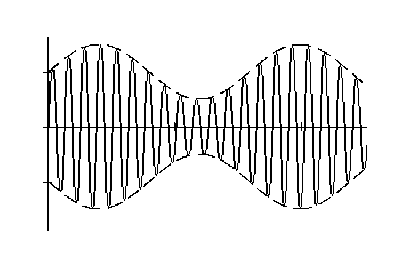
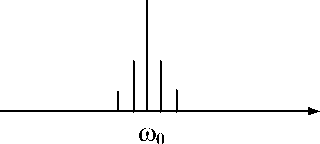
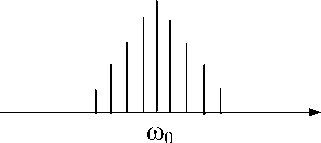
Pис.2. Схема процесса самомодуляции квазигармонической волны и эволюция ее спектра

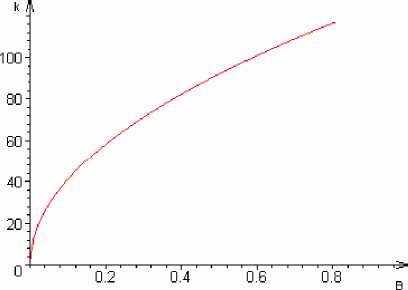
Рис.3. Увеличение области модуляционной неустойчивости с увеличением эффективной массы дислокаций

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 03-02-16924, грант № 05-01-00406) и фонда содействия отечественной науке.