Модуляционная неустойчивость волновых пакетов в неоднородных двухмодовых световодах

Волоконно-оптическим системам с межволновым взаимодействием в последнее время уделяется пристальное внимание, что объясняется широкими возможностями создания на их основе различных устройств управления лазерным излучением [1 –5]. В связи с этим актуальным является анализ динамики распространения волновых пакетов, формируемых двумя однонаправленными связанными волнами, с учётом различных нелинейных эффектов [6, 7]. Одним из таких эффектов, который может наблюдаться в световоде в результате проявления дисперсионных и нелинейных эффектов, является модуляционная неустойчивость (МН) квазинепрерывного оптического излучения при его временной модуляции [8– 11]. В настоящее время к исследованию этого эффекта проявляется значительный интерес, связанный с его фундаментальностью, а также с возможностью создания на его основе различных систем управления лазерным излучением.

Развитие МН должно учитываться при генерации субпикосекундных импульсов в волоконных лазерах и усилителях. В когерентных системах связи МН может приводить к «паразитной» амплитудной модуляции сигнала и быть нежелательной. С другой стороны, МН может использоваться для решения ряда важных технологических задач. Прежде всего, это генерация лазерных солитоноподобных импульсов со сверхвысокой частотой следования (свыше 1 THz). Подобные генераторы могут быть использованы для волоконно-оптических линий связи, использующих солитоны в качестве носителей информации. Системы, реализующие терагерцовую последовательность указанных импульсов, могут быть востребованы в метрологических технологиях [12, 13]. Следует также указать, что индуцированная МН может быть использована для создания полностью оптических логических элементов (например, оптического волоконного переключателя) [14, 15].

В одномодовом световоде с нелинейностью керровского типа МН волнового пакета возникает за счёт самовоздействия только в области аномальной дисперсии групповых скоростей (ДГС) [16, 17]. Для двухмодовых волновых пакетов кроссмодуляцион- ное взаимодействие мод [18, 19] может привести к МН в области частот, отвечающей нормальной ДГС. В последнее время большой интерес вызывает динамика импульсного излучения в световодах с неоднородным по длине распределением материальных параметров [20–22]. Наиболее широко используемым на практике типом неоднородности является экспоненциальный профиль ДГС [24 –25]. В этой связи в настоящей работе рассмотрены особенности возникновения и развития МН в двухмодовых световодах с неоднородностью дисперсионных параметров указанного профиля. В работе с учётом дисперсионных эффектов первых трёх порядков, кубической нелинейности, также линейной и нелинейной межмодовой связи исследуются условия возникновения МН, получены аналитические выражения для интегрального инкремента усиления гармонического возмущения и других важных характеристик, определяющих динамику МН в неоднородном двухмодовом световоде.

Уравнения для малых возмущений

Распространение в направлении оси z двух взаимодействующих волн, формирующих единый волновой пакет, при условии их фазового синхронизма, учёте дисперсии групповых скоростей, линейной и нелинейной связи волн описывается следующей системой уравнений для временных огибающих:

d A  1 d A

--L ₊-- L d z ul d t

. d, d2A i +

2 d t ²

⁺ i ( y c A , |² + Y k \^ J² ) A , = - i о A 3- , ,

где l = 1,2. Здесь u , = ( 3^/3® )^, в , и d_t - групповая скорость, константа распространения и дисперсия групповых скоростей соответствующей волны, ® 0 - несущая частота волнового пакета; о - параметр линейной связи, определяемый перекрытием профильных функций волнового поля мод, распространяющихся в световоде; y c и Y _k — параметры нелинейности, определяющие фазовую самомодуля-цию и кроссмодуляцию взаимодействующих волн [7, 8, 17].

При записи уравнений (1) используется приближение медленно меняющихся амплитуд, хорошо выполняющееся для волновых пакетов с несущей частотой свыше 10¹⁴ Гц и длительностью свыше 10^-13 с (при длине керровской нелинейности, значительно большей 1 м, т.е. у c\A,|² + y kA 3 - l|² <<  1 м ^{- 1}). Пренебрежимо малыми также считаются дисперсионные эффекты выше второго порядка и нелинейные эффекты высших порядков (нелинейности выше кубической, дисперсия нелинейности, рамановское саморас-сеяние и т.д.).

В дальнейшем будем считать, что световод обладает медленно меняющейся по его длине дисперсией, поэтому параметры d l = d l ( z ). Система уравнений (1) должна решаться совместно с начальными условиями для временных огибающих мод A l . В данной работе будем использовать начальные условия A 2 (0) = V A 1 (0), где значения v = ±1 отвечают симметричному и антисимметричному типам возбуждения световода.

Если длительность вводимого волнового пакета достаточно велика и применимо квазимонохромати-ческое приближение для волны накачки (т. е. пренебрежимо малы дисперсионные члены, что корректно для импульсов с начальной длительностью t 0 > 10 ^–9 s ), временные огибающие A i не зависят от времени t . С учётом указанных начальных условий для них могут быть получены точные стационарные решения системы уравнений (1):

A ^(z ) = Ine exp [^- i ( ⁽ Y c ⁺ Y k ) ¹ 0 ^-V^a ) z ] , (2)

где 1 ₀ = A l (0)| 2 - интенсивность вводимого в световод излучения. Для получения условий возникновения МН в структуре рассматриваемого типа в соответствии с общей схемой решения подобных задач [6, 7, 16, 17] введём в амплитуду стационарного решения (2) малое возмущение ф , ( z , t ):

A i ⁽ z , t ) =

= (4П + фi(z, t)) exp [i ((Yc + Yk)10 Va) z], для которого предполагается верным соотношение |фl (z, t)| ^/70 . Подставляя (3) в уравнения (1) и ли неаризуя их по возмущениям фl (z, t), получаем следующую систему уравнений, описывающую динамику возмущений:

^дф i 1 Эф i     d i д ² ф i

--1i2—г

д z u_i д t 2 д t

⁺ i¹ 0 ( Y c ⁽ ф i +ф i * ) + Y k ⁽ ф з - 1 +ф з - 1 * ) ) =                ⁽⁴⁾

= V i о ( ф з - 1 -ф i ).

Для гармонических волновых возмущений решение уравнений (4) можно представить в стандартном виде:

ф _i ( z , t ) = c_i cos( kz - Q t ) + ib , sin( kz - Q t ),           (5)

где k и Q = to ₀ - to v - волновое число и частота возмущения, to v - частота сигнальной возмущающей волны или спонтанного «шумового» возмущения.

Дисперсионное соотношение и его решения

Является стационарное решение (2) устойчивым либо неустойчивым к слабым возмущениям ф , ( z , t ), определяется типом решения соответствующего этим возмущениям дисперсионного уравнения. Для его получения подставим выражения (5) в (4), что приводит к системе четырёх однородных уравнений для амплитуд возмущения c_l и b_l :

Q    d, kc, c, +—Q2b = wa(b , - b,), l        I             ll V 3-1     /  '

^ul ²

kbi--bi +     dici + 210 (Ycci + Ykc 3-i) = ul2

= VO ⁽ c 3 - 1 ^- c , ).

Приравнивая определитель этой системы к нулю, получаем искомое дисперсионное уравнение:

K 12 K 22 -Г _C1D 1 K 22 -Г _c 2 D 2 K 1 ² -

-2v ГkK1K2a+ (Гc Гc2 - Гk2)D1D2 +

+(Гk2 -гС1Гc2)o2 = 0, где введены следующие обозначения: Q

K = k--, D = -A Q2 +фо, lul

Гc, = Di + 2Yc10, Гk = 2Yk10 - V^.

В общем случае решение уравнения (7) приводит к комплексным корням и, соответственно, к комплексным волновым числам возмущения. Неустойчивым решениям по отношению к малым гармоническим возмущениям (5) отвечают решения дисперсионного уравнения (7), для которых мнимая часть волнового числа k отлична от нуля. В этом случае возмущения (5) будут экспоненциально нарастать по длине световода, что означает неустойчивость рассматриваемых стационарных решений относительно волновых возмущений с частотой Q . Области положительных значений инкремента усиления g =2Im K определяют частотные области существования МН.

В аналитическом виде корни дисперсионного уравнения (7) могут быть определены лишь для некоторых частных случаев. Дальнейший анализ проведём для ситуации, реализующейся в системах с одним волноведущим каналом и в симметричных туннельно-связанных световодах. В этом случае с большой степенью точности можно считать d 1 = d ₂ = d , u 1 = u ₂ = u , при этом параметры D 1 = D 2 = D , Г c 1 = Г c 2 = Г c , K 1 = K 2 = K и дисперсионное уравнение принимает вид

K ⁴ - 2( Г c D +фоГ _k ) K ² + + ( Г c ² -Г _fc ²)( D ² -a ²) = 0.

Решениями этого уравнения являются следующие две дисперсионные ветви:

K 12 ( Q ) = d Q ² f d Q ² + 2 1 o ( Y _c + y k ) j ,

K 22 ( Q ) =                                          (9)

fd Q²_o jf d Q² , _ ,      . _o j

= I   — 2V° II — + 2Io(YcYk)-2V° I, откуда следует, что появление второй ветви обусловлено наличием межмодовой связи распространяющихся в световоде волн.

Условия и области существования МН

В качестве примера на основе анализа соотношений (8) рассмотрим условия возникновения МН в системе двух связанных волн, распространяющихся в световоде с экспоненциальным распределением ДГС по его длине:

d ( z ) = d ₀exp( - bz ).                             (10)

Данный тип неоднородности достаточно широко используется в полностью волоконных компрессорах оптических импульсов в связи с относительно простой технологией его реализации, обеспечивающей получение субпикосекундных солитоноподобных импульсов [16, 17, 22 – 24].

В однородном световоде инкремент усиления для каждого из типов возмущений определяется выражением g j ( Q ) = 2 Im K j ( Q ). В неоднородном по длине световоде МН носит интегральный характер, поэтому усиление возмущения на длине световода L должно определяться выражением:

L

G -(Q ) = J g j (z , Q )d z .                           (11)

Пусть в системе связанных волн отсутствует линейная связь, т.е. параметр о = 0 и межволновая связь реализуется только за счёт нелинейного крос-смодуляционого взаимодействия. В этом случае корни дисперсионного уравнения принимают вид

К² = ^ Q ² f d Q ² + 2 ( y c - ( - 1) ^j Y k ) I о j .        (12)

Развитию неустойчивости отвечают неравенства K j ² <  0 . В зависимости от знака и соотношения между параметрами, входящими в (11), возможны различные ситуации возникновения МН. Как показывает анализ (11), для волнового возмущения первого типа ( /' = 1), отвечающего решению K ₁( Q ) дисперсионного уравнения, МН будет существовать только в случае аномальной материальной дисперсии, т. е. при d <0. Область параметров, отвечающих МН, в этом случае определяется неравенством d >  4( y _c +Y _k ) 1 ₀/ Q ², а инкремент усиления имеет вид:

g 1⁽ z ) = ² Im К 1⁽ z ) =

= |Q| V4| d\ ( y c +Y k ) 1 0 - d ²Q2 .

С учётом заданного (10) профиля ДГС после интегрирования приходим к следующему выражению для интегрального инкремента усиления:

G 1 ( Q ) = у [V 4 1 0 I d 0I ( Y c +Y k ) - d 02 Q ² -

^-V ⁴ I 0 I d 0 I ( Y c ⁺ Y k ) e - ^b L ^- d 0 ^{2 Q} 2 e 2 ^{bL +}

⁴ I 0 ( y c ⁺ Y k ) I Q|

arctg

.   4 I0 (yc + Yk)

- arctg. ---------5----

V d ₀ Q ²

4 I0 (yc + Yk) I d 0IQ2

j

^{- 1}

I

e bL

-1

-

Для возмущения второго типа ( j =2), отвечающего ветви K ₂( Q ), МН может реализовываться как при аномальной, так и при нормальной дисперсии. В соответствии с (9), при аномальной дисперсии МН существует при выполнении условий d >- 4 ( y _c -Y _k ) 1 ₀/ Q 2 и Y _c > Y _k , а при нормальной - при выполнении условий d <  4 ( Y _k - Y _c ) 1 ₀ / Q ² и Y _c < Y _k . Инкремент усиления для этого типа возмущения в обоих случаях определяется выражением

g 2⁽ z ) = ^2Im K 2⁽ z ) =

= |^Q| V ⁴ I 0 | ^d ( z )( Y c ^-Y k )|^{- d} ( z ) 2 ^Q 2 .

Интегральный инкремент усиления для данного

случая примет вид:

G 2 (Q) = у [V 4 1 0 d 0 ( Y c -Y k )|- d 02 Q ² -

-V 4 1 0 | d 0 ( Y c -Y k )| e~ bL - d 02 Q ² e"^2bL +

⁴ I 0 |Y c ^-Y k| I Q|

- arctg

arctg

V

⁴ I 0 |Y c ^-Y k|

У I d 0IQ ²

⁴ I 0 |y c ^-Y k|

'N   I d 0IQ ²

Л

I

e ^bL

-

Область существования неустойчивых решений в рассмотренных случаях симметрична по частоте и включает в себя интервал частот ( -Q _c , Q _c ) , где для возмущений первого и второго типов предельные частоты

Q c 1 = 2

Q c 2

1/2

V ^{^Y} c W⁰^ I

= 2

I Y c ^-Y k| I 0 e^b L ^j

d ₀

,

Численный анализ

Ниже приведены результаты численного моделирования основных характеристик, определяющих процесс МН в двухмодовых световодах с экпоненци-альным профилем ДГС. В расчётах нами приняты: длина световода L = 100 м, параметр неоднородности b =5· 10^–3 м ^–1, групповая скорость u = 2· 10⁸ м/с, входная мощность I 0 = 1 Вт. Для параметров дисперсии и нелинейности используются типичные для кварцевых световодов значения.

На рис. 1 представлена частотная зависимость интегрального инкремента усиления G jj от частоты возмущения, полученная в отсутствие линейной межмодовой связи ( о = 0) для каждого из двух (j' =1,2) типов волновых возмущений, развивающихся в структуре. Приведённые зависимости отвечают следующим значениям параметров: d 0 = ( - 1) j • ( 0,625; 1,025; 1,425 ) - 10 ^{- 26} с²/м (кривые 1-3); у c = 10 ^{- 2} (Вт • м) ^{- 1} и у k = 2 - 10 ^{- 2} (Вт • м) ^{- 1} для у k = 10 ^{- 2} (Вт • м) ^{- 1} для второго типа возмущения. В связи с отсутствием в решениях (12) зависимости K j от параметра у полученные кривые справедливы как для случая симметричного возбуждения световода, так и для антисимметричного. Из приведённых кривых следует, что с увеличением модуля параметра дисперсии d частотная область существования МН сужается, а максимум инкремента усиления смещается в область меньших частот возмущения. Кривые усиления G j ( Q ) симметричны относительно смены знака Q , и на частоте возмущения Q = 0 усиление отсутствует. Величина пикового значения инкремента усиления G _m не зависит от величины дисперсии, а определяется лишь величиной мощности падающего излучения I ₀ . При этом величина частотной области, где реализуется МН, и максимальное значение инкремента усиления для волнового возмущения, определяемого ветвью K 1 ( Q , z ), при одних и тех же параметрах световода существенно больше, чем для возмущения, определяемого ветвью K ₂ ( Q , z ).

Исследуем теперь решения дисперсионного уравнения при наличии линейной и нелинейной межволновой связи, т.е. о^ 0 и у k ^ 0 . Для волнового возмущения, описываемого решением K ₂ ( Q , z ), МН имеет место при выполнении следующих неравенств:

уо- ( y c -Y _к ) 1 0 < d Q 2 /4 <уо, y c >Y k ,     (18a)

уо< d Q ² / 4 <уо+ ( y k -Y c ) 1 0 , Y c k •     (18b)

В соответствии с этими соотношениями МН должна иметь место в следующих случаях: при аномальной материальной дисперсии (d <0) и уо >0 только для yc > Yk, если же уо < 0 , то для уc > Yk и Yc < Yk; при нормальной материальной дисперсии (d > 0) и уо > 0 для yc > Yk и уc < Yk, если же уо < 0 , то только для Yc < Yk . В зависимости от со- отношения между входящими в (18) параметрами возможны различные реализации МН. Проведём более подробный анализ одной из таких возможностей.

Будем считать дисперсию аномальной ( d <  0) и уо >  0 . В этом случае МН реализуется только при ( Y _c - Y _k ) 1 ₀ > |о| в частотной области:

|Q| < 2V[уо- (Yc -Yk)I0 ]d"‘.

В случае d <  0 и уо < 0 частотный интервал МН зависит от соотношения параметров у _c и Y _k ■ Так, при ( Y _c - Y _k ) 1 ₀ > |о| для частотной области получаем

27уо/ d < |Q| < 2V[уо-(yc -Yk)10]d"‘.       (20)

В случае Y _k > Y _c имеются две возможности: при выполнении неравенства ( y _k -Y _c ) 1 ₀<|о| МН реализуется в области

2V[уо-(yc -Yk)10]d"‘ <|Q|< 27уо/ d,       (21)

а при ( y _c - Y _k ) 1 ₀ ^ |о| - в области 0 < |Q| <  27 уо / d .

Аналогичный анализ может быть проведён и для случая нормальной дисперсии, который здесь мы

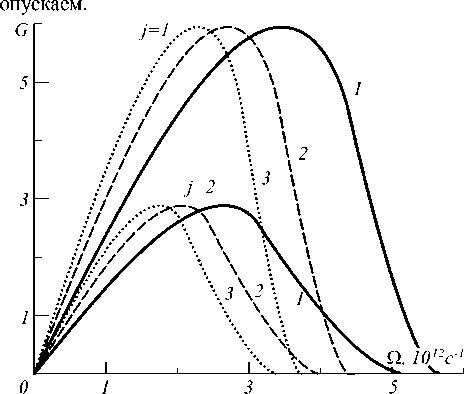
Рис. 1. Зависимость интегрального инкремента усиления от частоты возмущения в отсутствие межмодовой связи ( 0 = 0) для каждого из двух (j = 1, 2) типов волновых возмущений

На рис. 2 представлена зависимость инкремента усиления G от частоты возмущения Q , полученная для симметричного возбуждения световода ( у = 1 ), аномальной материальной дисперсии d =- 1,025 - 10 ^{- 26} с²/м, параметрах нелинейности      y _c = 2 - 10 ^{- 2}(Вт • м) ^{- 1}

Yk =10-2 (Вт • м)-1 и значениях параметра линейной связи о = (-0,55; -0,25; 0; 0,05; 0,25; 0,85)^10 -2м-1 (кривые 1 –6). В зависимости от соотношения между входящими в (18) параметрами возможны различные ситуации и области возникновения неустойчивости, каждой из которых соответствуют свои кривые. При о>0 (кривые 4-6) для зависимости G(Q) характерно неравенство нулю инкремента усиления при Q = 0, где он достигает максимального значения. С увеличением а область существования МН смещается в область меньших частот волновых возмущений. Для а = 0 (кривая 3) при Q = 0 усиление отсутствует, а область МН лежит в области частот (0, Qc). Величина максимума инкремента усиления Gm постоянна при взятых значениях а ввиду постоянства мощности 10. При а< 0 (кривые 1, 2) область существования МН берёт начало не от нуля частоты возмущения, а с частоты возмущения Qc 1 > 0 . С увеличением параметра линейной связи область существования МН увеличивается для зависимостей, не включающих значение частоты Q = 0 , и уменьшается для зависимостей, включающих это значение. Приведённые зависимости остаются справедливыми, если рассматривать антисимметричное возбуждение (^ = -1) и поменять знак параметра линейной связи на противоположный. При этом если в случае симметричного возбуждения световода при увеличении а область существования МН смещается на менее низкие частоты возмущения, то в случае антисимметричного -на более высокие частоты. Полученные зависимости G(Q) полностью соответствуют проведённому выше анализу характера их поведения и частотных областей МН.

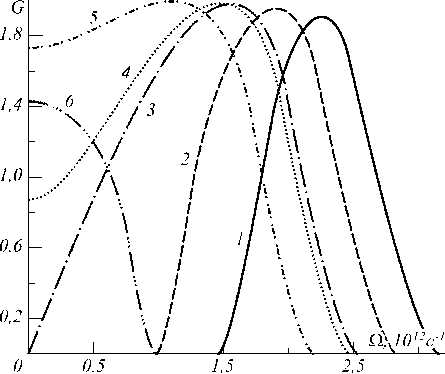
Рис. 2. Зависимость интегрального инкремента усиления от частоты возмущения при симметричном возбуждении световода, аномальной материальной дисперсии и σ = (–0,55; –0,25; 0; 0,05; 0,25; 0,85)×10 ^–2м ^–1 (кривые 1 – 6)

На рис. 3 приведены аналогичные зависимости G ( Q ) , полученные для симметричного возбуждения световода ( v = 1 ), нормальной материальной дисперсии d = 1,025 • 10 ^{- 26} с²/м, а также Y c = 2 • 10 ^{- 2} (Вт • м) ^{- 1}, Y k = 10 ^{- 2} (Вт • м) ^{- 1}. В рассматриваемом случае МН будет существовать лишь при а > 0 , поэтому выбраны следующие значения параметра линейной связи: а = (1,45; 1,15; 1; 0,85; 0,25; 0,05) • 10 ^{- 2} м^-1 (кривые 1-6).

Различные по характеру зависимости от а кривые G ( Q ), определяющие области возникновения МН, будут разделяться зависимостью, построенной при а = 10 ^-2м^-1 (на рис. 3 эти области были разделены зависимостью, построенной при а =0). При 0< а <10 ²м ¹ (кривые 4-6) на частоте возмущения Q = 0 инкремент усиления достигает экстремального значения. С увеличением а (от 0 до 10 ^-2м^-1) область существования МН смещается в область больших частот волновых возмущений. Для значения а =10 ^-2м ^- (кривая 3) на нулевой частоте возмущения усиление отсутствует, область существования МН определяется интервалом частот (0, Q c 1 ) и для зависимости G ( Q ) характерен единственный максимум. При а >10 ^-2м^-1 (кривые 1, 2) МН реализуется на интервале частот ( Q c 1 , Q c 2 ) . С увеличением линейной связи область существования МН смещается в область больших частот волновых возмущений.

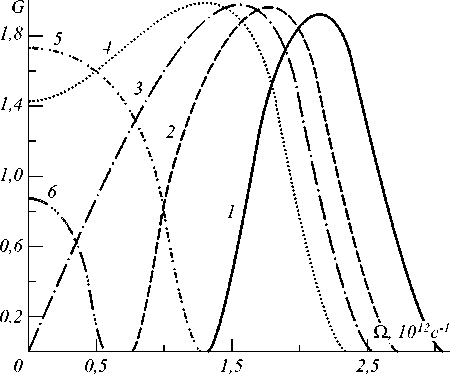
Рис. 3. Зависимость интегрального инкремента усиления от частоты возмущения при симметричном возбуждении световода, нормальной материальной дисперсии и σ = (1,45; 1,15; 1; 0,85; 0,25; 0,05)×10 ^–2м ^–1 (кривые 1 – 6)

Заключение

Проведённый анализ показывает, что динамика волнового пакета и условия возникновения МН во многом определяются величиной линейной и нелинейной межмодовой связи, дисперсии групповых скоростей и типом возбуждения световода. Важным результатом, следующим из получ енных соотношений, является возможность генерации ультракоротких импульсов в области частот, соответствующей нормальной материальной дисперсии, в отличие от одномодовых световодов, где МН возникает лишь при аномальной дисперсии. Известно, что развитие МН фактически вызывает генерацию коротких импульсов и сопровождается перекачкой части энергии исходных волн в спектральные компоненты, частоты которых отличны от начального значения несущей частоты волнового пакета [6, 16, 17]. Во временном представлении проявление МН состоит в частичном преобразовании ква-зистационарной волны (5) в периодическую после- довательность импульсов с периодом следования T ≅ 2π / Ωc . Отсюда ясно, что при реализации МН за счёт возмущения первой моды имеется возможность генерации ультракоротких импульсов, период следования которых (для стандартных значений параметров        кварцевых        световодов d ≅ 10-27 -10-26c2/м , (γc + γk ) I0 ≅ 1 м-1) составляет T ≅2π/Ωc1 ≅(1-3)⋅10-13c.

Это позволяет использовать для генерации ультракоротких импульсов наиболее распространённые и технически отработанные на сегодняшний день полупроводниковые лазеры, работающие в частотном диапазоне с λ < 0, 8µ m . Для большинства современных световодов эта спектральная область соответствует нормальной материальной дисперсии [6, 16, 17], а потому при одномодовом режиме работы указанные лазеры (и нелинейные световоды) не могут быть использованы в качестве генераторов ультракоротких импульсов. Предложенная двухмодовая схема реализации режима МН снимает эти ограничения. Отметим также, что кубическая нелинейность в ИК и видимом диапазонах практически линейно растёт с частотой [16, 17], поэтому значение керровской нелинейности, т.е. величина параметров γ c и γ k в видимом диапазоне (при прочих равных условиях), должна быть существенно выше, чем в ИК диапазоне. Следовательно, при реализации предложенной двухмодовой схемы генерации коротких импульсов с одинаковыми параметрами (длительность, частота повторения, амплитуда и т. д.) в УФ диапазоне частот можно использовать источники излучения значительно меньшей (по сравнению с ИК областью) мощности.

Работа выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 г.