Модулярные методы и алгоритмы деления на основе спуска ферма и итераций Ньютона
Автор: Червяков Н.И., Лавриненко И.Н.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.7, 2009 года.
Бесплатный доступ
В статье рассмотрены методы и алгоритмы деления на основе спуска Ферма и итераций Ньютона. Проведена их сравнительная оценка и определены диапазоны эффективного применения.
Короткий адрес: https://sciup.org/140191362
IDR: 140191362 | УДК: 681.3
Текст научной статьи Модулярные методы и алгоритмы деления на основе спуска ферма и итераций Ньютона
Введение. Постановка задачи
Главными целями процесса развития вычислительных средств были и остаются повышение их производительности и обеспечение высокой информационной и технической надежности. Как показывают многочисленные исследования, позиционная система свои возможности в этом направлении исчерпала. В связи с этим в последнее время проявляется значительный интерес к непозиционным системам счисления, а именно к системе остаточных классов, обладающей высоким уровнем естественного параллелизма при выполнении арифметических операций, высокой точностью, надежностью, способностью к само-коррекции. Однако широкое применение этой системы связано c трудностями, возникающими при реализации таких операций, как, например, деление. Операция деления в системе остаточных классов (как и в позиционной системе), является наиболее сложной и длинной [1]. Таким образом, для построения машинной арифметики на базе системы остаточных классов очень важным является вопрос разработки эффективного алгоритма для выполнения операции деления.
Модулярный метод и алгоритм деления на основе спуска Ферма
До последнего времени одним из самых эффективных модулярных методов деления считался итерационный метод спуска Ферма [2-3], суть которого заключается в следующем:
-
1. Делитель b переводится в обобщенную позиционную систему, то есть представляется в виде
-
2. Определяется приблизительный делитель b=Q-p\-P2 "-"Рк-Ъ где k – номер наиболее значимой ненулевой цифры представления делителя в обобщенной позиционной системе, Q определяется из таблицы, хранимой в памяти.
-
3. Вычисляется начальное приближение частного 4\ ^о/Н где а^ – делимое и значения .
-
4. Цикл из r итераций, в процессе которых вычисляются значения 41 =к-1 / ь\ и а, =сц_\ -b-qj при i = 2;3...r . Выполнение итераций продолжается до тех пор не будет выполнено условие Qi — ^ , либо до at = 0 -
-
5. Определяется частное от деления
и и—1
Й = ЙИ+1П^ +ЬпПрг ^-^PtPi + biPi + bA- /=1 /=1
где Рх ,Р2 - Ри – основания системы и определяется наиболее значимая ненулевая цифра Ьр этого представления (на основе представления ортогональных базисов в обобщенной позиционной системе [4]).
Ч — 41 "42 4r-1 "*" 4г ’ где qr,если qr фОи аг = О
4 г
< \,если О, во
qr = Ои ar_\ > b для любых b ^0. всех остальных случаях
Рассмотренный итерационный модулярный метод общего деления на основе метода спуска Ферма является эффективным, простым в реализации. Он может быть легко модифицирован на язык кольцевых операций системы остаточных классов. Представленная в частном ошибка при выполнении итераций уменьшается до нуля. Так, если допустимая ошибка задана не выше 0,1; то достаточно провести всего четыре итерации.
Недостатком метода деления на основе спуска Ферма является то, что в случае если разрядности делимого и делителя отличаются значительно, то для вычисления округленного частного может потребоваться много итераций. В связи с этим возникла необходимость разработки алгоритма деления лишенного подобного недостатка.
Метод и алгоритм целочисленного деления на основе итераций Ньютона
Для реализации итераций Ньютона необходимо использование расширенной системы остаточных классов, которая определяет вычислительный диапазон для промежуточных значений, равный приблизительно квадрату от соответству- ющего нормального диапазона. Для этого система оснований выбирается специальным образом. Пусть 4Х’42’-’42п – простые числа, для которых выполняется условие
!1 <42 <-<42п-Х <42п’ (1)
Если g=r-b>0, , то \а) b J = q +1, иначе \alb\ = q.
Для того, чтобы обосновать сходимость процесса нахождения обратной величины \_M!b\, нужно сначала доказать вспомогательное неравенство:
где и е Z, и > 1. Разобьем эти числа на две группы следующим образом:
^1=?Ь Р2=43’ Р3=45 - Ри=42п-\"Л^
Ь1м\м1ь-г^
Оно следует из определения оператора
Рт-Х 42’ Рп+2 44- РпРЗ 46 •■■ Р2п 42п- Р)
(наименьшее целое число превосходящее
X
, то есть ^<1^ |
Тогда РХ’Р2 - Р2п – основания расширенной системы, а РХ’Р2 - Рп – основания базовой системы; Рп + Х’Рп + 2 ••• Р2п – основания расширения базовой системы до расширенной;
M/b - Z/+1 = M/b - 2Zj +1 bZ^ ]m\<
< Mlb - 2ZZ +bzj IM + \ = b/M ^Mlb - Z,- )2 +1.
2п п __ 2п
^П^ ’ м=Т1р' ’м= ГЬ -
7=1 7=1 7=77 + 1
соответствующие диапазоны.
Алгоритм деления, основанный на итерациях Ньютона, состоит из двух этапов: вычисление целочисленной обратной величины для делителя ь по отношению к нормальному диапазону и нахождение частного [5-6].
Для вычисления обратной величины \_М/Ь\ используется метод итераций Ньютона. Применяя схему итераций Ньютона
^7 + 1 =Zi-.f^i^fkZi^
Аналогично доказывается левая часть выражения (7).
Алгоритм нахождения обратной величины Uw^j конечен для любого значения b , удовлетворяющего условию \
При Zx =2и b > L3M/4J итерации останавливаются на значениях.
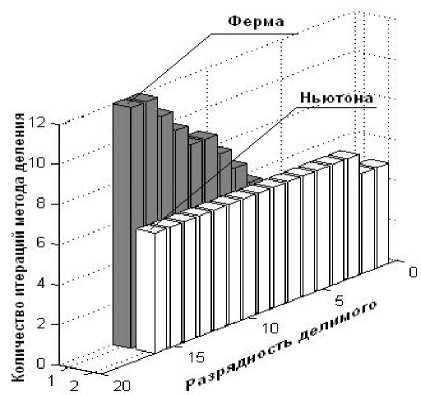
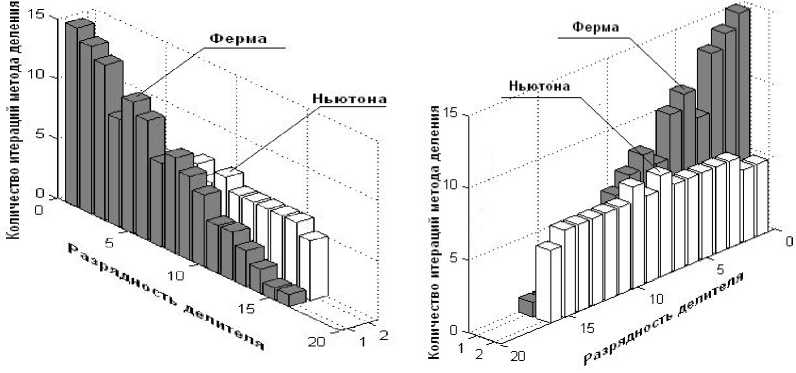
При условии LM/2j? При условии \ для 7 = 1 =>M/b-Zx >M/M/2-2 = 0; для i > 1 с учетом левой части выражения (7) . для f^ = M[zi -b и Г^=-М^, получаем следующую рекурсию Zi+X = zi Цл^ -b"z^^мУг^^М-Ь-г^М. В системе остаточных классов используется только целочисленное деление, поэтому окончательная версия примет вид: Следовательно, выполняются неравенства bZi M M следует справедливость оценки Zz' + i — 2Zz- M > 2Zj — Zj = Zj • ^7 +1 - Z^M-bZ^=2Z bZ? M В качестве начального приближения можно выбрать z\ = 2 и продолжать вычисления до тех пор, пока выполняется условие Zi+X * zi ■ При -7+1 — zi вычисления прекращаются, и проверяется условие: t = M - b • Zj+[ -b< 0 . (6) Если это условие верное, то обратная величина будет равна ^/^=“7 + !, иначе VM/b^ = zi+1 +1. Второй этап деления а на b состоит в нахождении частного из равенства 4 = \ka-zi+xMM\- Это означает, что последовательность моно- тонно возрастает и условие остановки алгоритма Zz+i=2Zz- bZ7 будет в итоге достигнуто. На обоих этапах разработанного метода и алгоритма деления главной операцией является операция масштабирования числом M ,которая может быть выполнена наоснове разработанного методапредставле-ния ортогональных базисов в обобщенной позиционной системе [4]. На первом этапе алгоритма деления условие оста-новкиалгоритма “7 + 1 — zi.Двацелыхчисла a и b всис- теме представлении равны тогда и только тогда,когда равны их соответствующие компоненты:a, = b, .При реализации в ЭВМ проверка на равенство для каждой компоненты может быть выполнена в двоичном коде с помощью логической операции AND. Кроме того,для выполнения корректирующего шага на обоих этапах разработанного метода деления на базе итераций Ньютона необходима одна операция сравнения.Онаможетбытьвыполненанаоснове представления в обобщенной позиционной системе [4]. Для того чтобы ускорить процесс нахождения обратной величины M/b нужно в качестве начального приближения вместо значения Zj =2 выбрать ближайшую степень двойки.То есть выбрать начальное значение в видеZ] =2 ,где K определяется из условия . Сравнительная оценка методов деления на основе спуска Ферма и итераций Ньютона Методы Ферма и Ньютона являются итерационными. Поэтому их сравнение нужно проводить по двум критериям: - по числу операций, выполняемых за одну итерацию; - по общему числу выполняемых итераций. Эти методы имеют различную структуру, и число повторений входящих в них циклов зависит от разных параметров. По этой причине выполнить их точную сравнительную оценку по общему числу операций затруднительно, поэтому она была проведена приближенно. Для этого на рисунках, изображающих схемы алгоритмов Ферма и Ньютона были пронумерованы шаги, которые соответствуют по виду и по числу выполняемых арифметических операций. В результате этой оценки был сделан вывод о том, что алгоритмы Ферма и Ньютона при условии выполнения только одной итерации имеют приблизительно одинаковую вычислительную сложность. Сравнительная оценка общего количества итераций, выполняемых в алгоритмах Ферма и Ньютона, приведена на рис.1-2. Рис. 1. Оценка числа итераций методов Ферма и Ньютона в зависимости от разрядности делимого Рис. 2. Оценка числа итераций методов Ферма и Ньютона в зависимости от разрядности делителя Эта оценка проводилась на основе компьютерного моделирования в системе MATLAB. В первом случае (см. рис. 1 ) значение делителя фиксировалось, а значение делимого менялось. Во втором случае (см. рис. 2), наоборот, неизменным оставалось значение делимого, делитель принимал различные значения. Проведенная сравнительная оценка показывает, что количество итераций метода Ферма растет вместе с ростом разницы между разрядностями делимого и делителя. Количество итераций метода Ньютона от этого не зависит. Поэтому, если разница между разрядностями делимого и делителя является достаточно большой, то в этом случае отличный результат дает применение метода Ньютона. Однако если разница небольшая, то выгоднее применять для выполнения операции деления метод Ферма. В таблице 1 приведена оценка числа итераций методов Ферма и Ньютона для случая, когда в качестве делителя выбиралось шестиразрядное число, а разрядность делимого изменялась. Оценка выполнена с помощью Таблица 1. Оценка числа итераций методов деления Ферма и Ньютона Выводы Проведенная сравнительная оценка показала, что методы деления Ферма и Ньютона при условии выполнения только одной итерации имеют приблизительно одинаковую вычислительную сложность. Если выполняется деление чисел одинаковой разрядности или если их разрядность отличается незначительно, то для достижения лучшего результата выгоднее применение метода Ферма. Если разрядности делимого и делителя отличаются незначительно, огромное преимущество по времени выполнения деления дает применение метода Ньютона.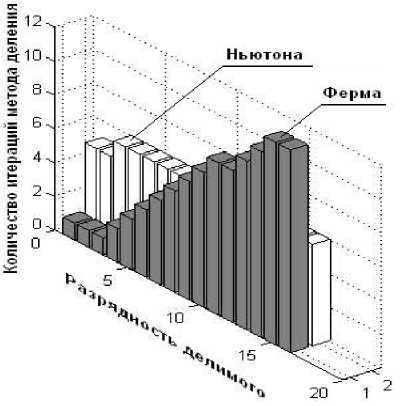
Разрядность делимого
Число итераций метода
= F/N
Ферма(F)
Ньютона(N
8
5
6
0,8
16
12
6
2
32
25
6
4,2
64
53
6
8,8
128
105
6
17,5
256
203
6
33,8
512
411
6
68,5
1024
829
6
138,2
программ, разработанных в среде MATLAB, реализующих методы Ферма и Ньютона.
Список литературы Модулярные методы и алгоритмы деления на основе спуска ферма и итераций Ньютона
- Галушкин А.И., Червяков Н.И. Нейрокомпьютеры в остаточных классах. М.: Радиотехника, 2003. -270 с. 2.
- Червяков Н.И., Лавриненко И.Н., Лавриненко С.В., Мезенцева О.С. Методы и алгоритмы округления, масштабирования и деления чисел в модулярной арифметике/Труды Юбилейной МНТК «50 лет модулярной арифметике» в рамках V МНТК «Электроника и информатика-2005». М.: 2006. -С. 291-310.
- Лавриненко И.Н. Деление чисел, представленных в системе остаточных классов//ИКТ. Т.3, №3, 2005. -С. 6-9.
- Червяков Н.И. Методы масштабирования модулярных чисел, используемые при цифровой обработке сигналов//ИКТ. Т.4, №3, 2006. -C. 15-23.
- Червяков Н.И., Лобес М.В. Целочисленное деление в системе остаточных классов//Материалы III МНТК «Инфокоммуникаци-онные технологии в науке, производстве и образовании». Ч.III. Изд. СевКавГТУ, 2008. -С. 198-204.
- Червяков Н.И., Лобес М.В. Алгоритм целочисленного деления в системе остаточных классов//ИКТ. Т.5, №4, 2007. -С. 8-13.


