Моды планарного градиентного гиперболического секансного волновода

В последнее время возрос интерес к планарным градиентным и фотонно-кристаллическим линзам, которые способны обеспечить субволновую фокусировку лазерного света [1-4]. Они применяются для ультракомпактного сопряжения планарных волноводов разной ширины [5]. В качестве планарной градиентной линзы используется линза, показатель преломления которой зависит от поперечной координаты как гиперболический секанс. Гиперболическая секансная (ГС) линза имеет свою долгую историю. Еще в 1930 году П.С. Эпштейн [6] рассмотрел задачу расчета мод для градиентного волновода со сложным показателем преломления, обобщающим ГС-профиль. В 1951 году А.Л. Микаэлян [7] нашел, что ГС-профиль показателя преломления является оптимальным для фокусировки света. Поэтому ГС-линза Мик аэляна является частны м случаем градиентного волновода Эпштейна. Далее задача распространения света в ГС-волноводе и ГС-линзе решалась в геометрооптическом [8,9], квазиоптическом [10] и волновом [11-14] приближениях. В [15,16] описаны экспериментальные результаты по фокусировке света с помощью ГС-линзы. В [17] ГС-линза используется для сверхразрешения совместно с рефракционной и дифракционной линзами. В известной монографии М. Адамса [18] дан обзор работ по волноводам Эпштейна и ГС-волноводам.

В данной работе получено выражение для периода Тальбота (или фокусного расстояния) для ТЕ-мод в планарном ГС-волноводе и показано, что для ТМ-мод не возникает аналогичная периодичность и нет фокусировки в ГС-волноводе. Показано, что в ГС-волноводе с «пьедесталом» для ТЕ-мод эффект Тальбота и фокусировки также отсутствуют.

Получены выражения для полной ширины по полуспад у интенсивности и нормированной интенсивности для основной ТЕ-моды в ГС-волноводе. Найдены параметры ГС-волновода, при которых ширина основной моды минимальна, а ее интенсивность на оси волновода максимальна.

1. ТЕ-моды планарного ГС-волновода

Рассмотрим планарный ГС-волновод с зависимостью показателя преломления вида

n

n(x)=           , ch (x/ a)

где n – показатель преломления на оси z при x =0, x – поперечная координата волновода, a – полуширина волновода по спаду показателя преломления в 1,54 раза. На рис. 1 показан профиль (1) ГС-волновода для n =3,47 и a = λ/2=0,775 мкм, λ = 1,55 мкм – длина волны света.

Решение уравнения Максвелла для монохроматического света для ТЕ-поляризации сводится к решению уравнения Г ельмгольца для проекции электрического вектора E y на ось y , которая перпендикулярна плоскости волновода ( x , z )

1 2 /д ² _, 2, .

+ *? + k n ⁽ x )

E y ( x , z ) = 0,

где k = 2π/λ – волновое число света. С учетом (1) и используя разделени е переменных

E y ( x , z ) = exp ( i P z/a ) E ( x ) ,                      (3)

уравнение (2) сводится к уравнению для E ( x ):

d²       k ² n ²       в ²

+ dx2   ch2 (x]a) a2

E ( x) = 0,

где β – безразмерная постоянная распространения. Решение уравнения (4) можно найти аналогично решению скалярного уравнения для волновода Эпштейна [18].

п(х) , 3,0

2,5

2,0

1,5

1,0

0,5

-8

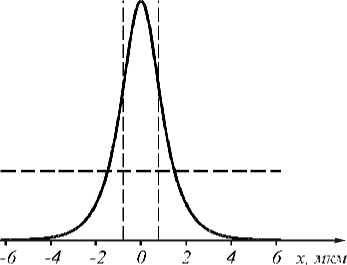
Рис. 1. Зависимость показателя преломления от координаты для ГС-волновода (1).

Вертикальные пунктирные линии при x=±a, горизонтальная линия при n(x)=1

Сделав замену переменных y = exp(2x/a) и разделив полученное уравнение на 4y2/a2, получим d2 1 d    k2a2n2     p2

+    +       - dУ   У dУ y (1 + y) 4 У

E ( У ) = 0.

E 1 ( x , z ) -

Заменим функцию E(y ) на y p (1+ y ) q V ( y ), где p и q – параметры, которые будут определены ниже. Подставив это решение в (5) и разделив уравнение на y^{p - 1} ( 1 + y ) ^{q - 1}, получим:

y (1 + y )V"+ [(2 p +1)(1 + y)+ 2 qy ] T'+

+ f p2 -P-) 1+y V + q (q -1)V +

I 4 J у

+ ( 2 p + 1 ) q V + [ k ² a ² n ²

V

- q(q -1)]      - °.

1 + y

При p = p /2 и q = [1-(1+4 k ² a ² n ²)^1/2]/2 уравнение (6) преобразуется в гипергеометрическое дифференциальное уравнение [19, формула 15.5.1]:

y (1 + y )V"+{( 2 p +1) + [(q + 2 p) + q +1] y }V‘+ + (q + 2 p) q V - 0,

решением которого являются гипергеометрические функц ии 2 F 1 ( q +2 p , q ; 2 p +1; – y ). Чтобы полученное решение обладало конечной энергией, первый параметр гипергеометрической ф ункци и выберем целым отрицательным числом – m (в этом случае ф ункция становится многочленом). Тогда решение уравнения (4) имеет след ующий вид

У ^в/ 2 2 F 1 (^- m , ^- m ^- P , ^p+ 1, ^- У )

Em (У )-           (1 + y)P+m

Учитывая, что y = exp( 2x/a ), получим выражение для ТЕ-мод ГС-волновода

^E m ( x , z )^-

exp ( z p z/a ) ₂ F ( - m , - m - p , P+ 1, - y )

,(9)

ch ^p ( x/a )( 1 + y ) m

где y = exp( 2x/a ), m – положительное целое число. Уравнение для нахождения постоянных распространения мод (дисперсионное уравнение) имеет вид

2 в - V 1 + 4 k ² a ² n ² - ( 2 m + 1 ) .

Уравнение (10) получается из условия, что амплитуда (9) будет ограниченной при условии, что b =– m . В этом случае гипергеометрическая фун кция становится многочленом. Сама гипергеометрическая функция имеет вид [19]

“ (b) (c) pp

2 F 1 ( b , c , d , x ) - ^ ^{p p} — , (11) p - 0 ( ^d ) p p !

где ( b ) _p = Г ( b + p )/ Г ( b ) - символ Похгаммера. Из (9) можно получить три первые ТЕ-моды ГС-волновода ( m =0,1,2)

E 0 ( ^x , ^z )^-

exp ( z p z/a ) ch ^p ( x/a )

- exp ( z p z/a ) sh ( x/a ) ch ^{p+ 1} ( x/a )

exp ( z p z/a )

sh² ( x(a )

E 2 ( x , z ) -

ch ^{p+ 2} ( x/a )

2 ( p + 1 )

На рис. 2 показаны амплитуды (9) при z = 0 первых четырех ТЕ-мод ГС-волновода (рис. 2 а ) и амплитуда десятой моды (рис. 2 б ). Из рис. 2 видно, что с ростом номера моды число локальных «лепестков» моды увеличивается, а их размер вблизи оптической оси уменьшается. Из рис. 2 можно оценить, что ширина модуля амплитуды (по полуспад у) основной моды равна примерно а = λ/2, а ширина локального максимума десятой моды ( m = 10) – a /6= λ/12. Заметим, что из (10) следует , что максимальный номер моды, при котором β еще положительно, равен M - [ P ₀ ] , где P ₀ - (V 1 + 4 k ² a ² n ² - 1 ) ^2, [ P 0 ] - знак целой части числа p ₀ ( M = 10 при а = А/2).

Из (1) видно, что показатель преломления ГС-волновода меняется от n до нуля. Хотя в реальности он не может быть меньше 1. Поэтому моды (9) являются модельными модами, которые отличаются от мод реальных ограниченных волноводов или волноводов с оболочкой.

Случай ограниченного волновода будет рассмотрен в разделе 4. С модельностью мод (9) связано, в частности, ограничение на число мод, которое следует из (10) m < M -[Р0 ]. Аналогичная ситуация возникает и для параболического волновода [18]. Но при теоретическом исследовании это обстоятельство игнорируют и считают, что ГС-волновод имеет счетный и полный базис модовых фун кций (9), хотя моды (9) не ортогональны и ненормированы. С учетом сказанного любое световое поле в ГС-волноводе (1) можно разложить по базисным функциям (9)

ю

E ( x , z ) = S ^C m exp ( i^ m z/a ) ^ m ( x ) ,          ⁽¹⁵⁾

m = 0

где у ( x ) = 2 F (" m, — m "I3 m , в m + 1, - У ) m            chem (x/a )(1 + y)m

Сm – коэффициенты разложения, βm – этим обозна- чением показано, что постоянные распространения β зависят от номера моды. В выражении для постоянной распространения (10) можно выделить слагаемое, не зависящее от номера m, и вынести за знак суммы соответствующий сомножитель:

E ( x , z ) =

^

= exp (iPozla ) S Cm exp ("imz a )T m ( x ), m =0

где в₀ = (V1 + 4 k²a²n ² - 1) / 2 .

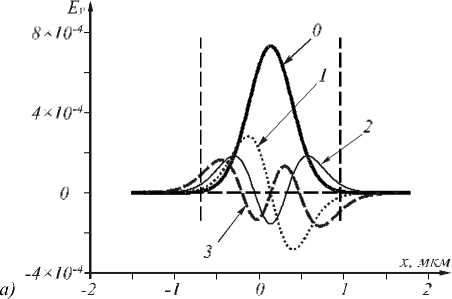
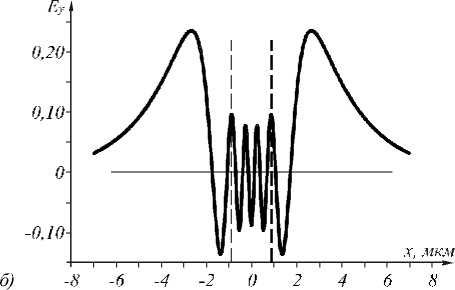
Рис. 2. Графики при z = 0 амплитуд (9) первых четырех мод (а): m = 0 (кривая 0), m = 1 (кривая 1), m = 2 (кривая 2), m = 3 (кривая 3) и график десятой моды m = 10 (б).

Вертикальные пунктирные линии при x = ±a

Из (17) следует, что на расстоянии

L = 2πa (18) разности фаз межд у модами (16) станут такими же, какими они были при z = 0. То есть световое поле (17) будет повторяться с периодом L. Поэтому величина (18) называется периодом Тальбота. Если вме- сто бесконечно протяженного ГС-волновода рассмотреть только его часть от z =0 до z = L/2, то освещая такую ГС-линзу плоской ТЕ-волной со стороны z =0 на выходе линзы при z = L/2 сформируется фокус: все лучи, параллельные оптической оси, соберутся в одну точку на оптической оси. Поэтому расстояние L/2 можно назвать фокусным расстоянием ГС-линзы .

С помощью (12) можно найти ширину основной ТЕ-моды из условия по полуспаду интенсивности

• 10 (x, z ) = ch-2e( x/a ) = 1/2.(19)

Из (19) следует выражение для ширины основной моды:

FWHM = 2a ln(21/(2в)+ V21/e -1).(20)

На рис. 3 показана зависимость ширины основной моды ( FWHM ), умноженной на kn , от безразмерной ширины волновода kan .

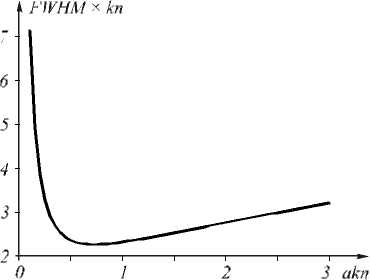
Рис. 3. Зависимость ширины основной ТЕ-моды (20) от безразмерной ширины ГС-волновода

На рис. 3 мини мальная ширина основной моды равна ( n =3,47)

FWHM = 226 = 0,111,(21)

kn кото рая достигается при ширине волновод а a = 0,72/ (kn ) = 0,031.

При a =0,03λ ширина волновода равна 178 нм (0,115λ). Именно при такой ширине показатель преломления спадает от максимума в центре до единицы на краю. Численное моделирование конечноразностным методом FDTD показало, что и при такой ширине в волноводе распространяется ф унда-ментальная мода E 0 ( x , z ). Ширина такой моды по полуспад у оказывается меньше, чем предсказывает формула (21): 0,05λ. Это можно объяснить тем, что формула (21) получена для волновода бесконечной ширины, в то время как при моделировании использовался волновод шириной 178 нм.

Если нормировать основную ТЕ-моду (12) на единичную энергию ^

^A I ch²" ( x/a ) ^{= 11                         (22)}

где

" 2^{1 - 2 в} 0 Г(2 в ₀) . а Г 2 ( в о )

A – нормировочная константа, Г( х ) – гамма-функция [19], то получим выражение для интенсивности нормированной основной моды:

2^{1 - 2 в о} Г ( 2 в о )

^{0 (} x ) а Г² ( р ₀ ) ch^{2 e} ( Ха ) .

На рис. 4 показан а зависимость максимальной интенсивности (в произвольных единицах) основной ТЕ-моды на оптической оси ГС-волновода от безразмерной ширины волновода kan .

ничивать волновод с показат елем (1) условием n ( x ) > 1, которое приводит к видоизменению световых мод, распространяющихся в среде. Решение уравнения (2) для ТЕ-мод в среде с показателем (25) имеет вид

Em ( Х, Z ) =

= exp ( г в z/а ) ₂ F 1 ( - m , - m -Y , Y+ 1, - У )          ⁽²⁶⁾

ch ^Y ( x/а ) ( 1 + y ) m

где

2 y= 2V в ² - k ² а ² n ² = 4 1 + 4 k ² а ² n ² - ( 2 m + 1 ) . (27)

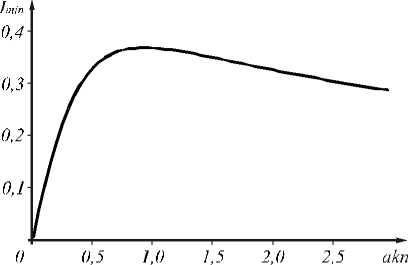
Рис. 4. Зависимость максимальной интенсивности основной моды на оптической оси ГС-волновода от безразмерной ширины волновода kan

Из рис. 4 след ует, что интенсивность основной моды на оптической оси будет максимальна при ширине волновода а = 0,93/ ( kn ) = 0,04 Х . Из сравнения рис. 3 и 4 видно, что минимальная ширина моды и максимальная интенсивность моды на оси достигаются при разных значениях ширины волновода: а = 0,72/ ( kn ) = 0,03 Х и а = 0,93/ ( kn ) = 0,04 Х , хотя размеры этих волноводов существенно субволновые (λ = 1,55 мкм): 2 a = 93 нм и 2 a = 124 нм. Заметим: в [20, 21] показано, что для ступенчатых кварцевых волокон ( n = 1,44 и λ = 1,55 мкм) минимальный диаметр составляет 0,2λ. В этом случае более 97% энергии моды распространяется за волокном. При диаметре меньше 0,2λ резко возрастают оптические потери в волноводе, связанные с флуктуациями его диаметра и шероховатостями на его поверхности. Однако в [22] было изготовлено кварцевое проволочное (без оболочки) волокно диаметром 50 нм с потерями всего 0,1 Дб/мм.

Все обозначения в (26) такие же, как в (9). Из (27) следует уравнение для постоянных распространения ТЕ-мод в ГС-волноводе с «пьедесталом»

₂ 1/2

в = < k²а²n ² +—|^ 4 1 + 4 k²а²n ² -( 2 m + 1 ) ] . (28)

Из (28) следует, что нельзя ввести период Тальбота (18), так как в выражении для β нельзя выделить аддитивное слагаемое, зависящее от номера моды m , как это было сделано для выражения (10). То есть, несмотря на то, что показатель преломления ГС-волновода с «пьедесталом» (25) удобнее, чем показатель (1), при практической реализации ГС-линзы, но такая линза не будет обладать свойством «идеальной» фокусировки, когда все лучи, параллельные оптической оси, собираются в одной точке фокуса.

3. ТМ-моды ГС-волновода

Уравнение Гельмгольца для план арного волновода с показателем преломления n ²( x ) = ε( x ) для ТМ-поляризованной волны имеет вид

⁵² V¹2 ^2 4 1

У ^ + kn (x)-

1 de(x) д г(x) dx дx

H_y ( x , z ) = 0,

2. ТЕ-моды ГС-волновода с «пьедесталом»

У планарного ГС-волновода с «пьедесталом»

след ующая зависимость показателя преломления от поперечной координаты

n ² ( x ) = n ² +

( n ² - n i2 ) ch² ( x/а )

где n 1 – показатель преломления среды, в которой создан градиентный волновод. Наличи е среды с показателем преломления n 1 > 1 позволяет не огра-

где H y ( x,z ) – комплексная амплитуда проекции на ось y магнитного вектора волны. Разделяя переменные H y ( x,z ) = exp ( i β z/a ) H ( x ), для функции H ( x ) получим уравнение

^{d 1} d £^{( x} ) ^d     2 2 ^в

—2 —-- + k n ( x ) - 2

d x e ( x ) d x d x а

xH (x ) = 0.

x

После замены H ( x ) = n ( x ) F ( x ) уравнение (30) сво-

дится к уравнению

d²       1 d² e ( x )

d x² 2 г ( x ) d² x

^^^^^^e

• 3    I 1 ^{d £}( ^x ) I . ,2 2          в ²

+ k n (x)

• 4    /г ( x ) d x J               а ²

F (x ) = 0.

Для ГС-волновода (1) вместо (31) получим

d

I k n dx ² ^ ch ² ( x/a )

a ²

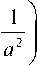
F ( x ) = 0.

2— 2 F 1 ⁽P ⁺ d , d , P ⁺ 1, ^- y 0 ^{)( 1 +} y 0 ) y o ^{2 +} d y

Если ввести параметр η² = β² + 1, то уравнение (32) будет эквивалентно уравнению (4) для ТЕ-по-ляризации . Тогда, c учетом решения (9), решение уравнения (29) для ТМ-мод ГС-волновода будет иметь вид

^H m ( x , z ) =

_ exp ( i p z/a ) ₂ F ( - m , - m -n , n + 1, - У ) ,      (33)

ch ⁿ ( x/a )( 1 + y ) m

2 I , P)     P

⁺ a x y 0 ⁺ 1 x ^{+ d +}-1 y 0 ⁺ 2 ^x

x 2 F 1 ( p + d , d , P + 1, - y 0 ) _ 0.

Уравнение (38) можно решить только численно. При этом можно воспользоваться рекуррентной формулой для гипергеометрических функций [19]

где

2 П _ 2V в ² + 1 _ V 1 + 4 k²a ² n ² - ( 2 m + 1 ) .       (34)

Из (34) следует дисперсионное уравнение для нахождения постоянных распространения ТМ-мод p_14[V1 + 4k2a2n2 -(2m +1)]2 -1.      (35)

Так как в (35), аналогично (28), нельзя выделить аддитивное слагаемое, зависящее от номера моды m , то значит ТМ-поляризованное излучение не фокусируется ГС-линзой и нельзя ввести период Тальбота, аналогичный (18). Из (34) следует, что при 0< η < 1 постоянная распространения моды β будет комплексной величиной. Это означает, что в ГС-волноводах с шириной a <  72/( kn ) не будут распространяться световые моды с ТМ-поляризацией, а возможны только вытекающие моды.

d

2 F1(A, B, C, x) _ dx

AR

_ c ₂ F 1 (A + 1, B + 1, C + 1, x ).

5. Моделирование пр охождения ТЕ-мод в ГС-волноводе

С помощью программы FullWAVE (RSoft), реализующей FDTD-метод разностного решения системы уравнений Максвелла, было промоделировано распространение в ГС-волноводе ТЕ-мод (9). ГС-волновод выбирался ограниченным (36). Параметры моделирования были следующие: a = λ / 2, λ = 1,55 мкм, n = 3,47, ГС-волновод (36) ограничен размером b = 1,5 мкм. На рис. 5 показаны мгновенные распределения реальной части Е -вектора ТЕ-волны, распро страняю-щиеся в одном и том же ГС-волноводе (вертикальные и горизонтальные линии ограничивают волновод).

4. ТЕ-моды ограниченного ГС-волновода

ГС-волновод (1) практически нереализуемый, так как n ( x ) ^ 0 при | x | ^ ^ . Поэтому рассмотрим

ограниченный ГС-волновод

^{n (} x ) ^_ <

n ch (x/ a)

| x | <  b ,

1, | x >  b ,

где b _ a In ( n + 7 n ² - 1 )/2

найдено из уравнения

n ( b )= 1. Решение уравнения (2) для ТЕ-мод в ГС-волноводе с показателем (36) имеет вид

E_y ( x , z ) _ exp ( i p z/a ) x

x ^

2 F 1 ( P+ d , d , p+ 1, - y ) ( 1 + y ) d y ^{e /2},

_ | x <  b ,                                          (37)

2 F 1 ⁽ P + d , d , P + 1, ^- y o ) ( 1 ⁺ y 0 ) d y о ^в /2 e ^X ( b - x ⁾, . | x | >  b ,

где d _ (1 - 71 + 4k2 a2 n2)/2 , в2 = X2 +k2, y0 = exp(2b/a).

б)

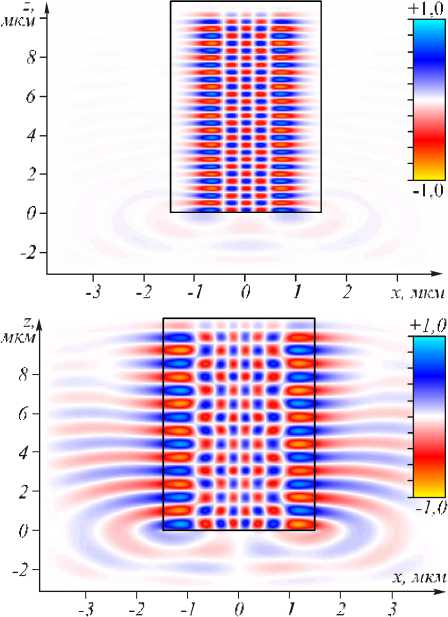
Рис. 5. Мгновенная картина р еальной части амплитуды напряженности электрического поля, распространяющегося в ГС-волноводе (снизу вверх). На вход волновода при z = 0 подавались ТЕ-моды (9) с номерами m = 4 (а) и m = 7 (б)

Дисперсионное уравнение для нахождения констант распространения β имеет вид

На вход волновода ( z = 0) подавались ТЕ-моды (9) с номерами m = 4 (рис. 5 а ) и m = 7 (рис. 5 б ) и с параметром a = λ / 2. Из рис. 5 видно , что начальные моды продолжают распространяться в во лно-воде почти без искажений. Из рис. 5 б мо жно определить , что ширина локального максимума амплитуды по полуспаду интенсивности равна FWHM = 0,065λ.

На рис. 6 показана мгновенная картина реальной части напряженности электрического поля внутри такого же ГС-волновода, как на рис. 5, но на вход ( z =0) подавалась ТЕ-мода (9) с номером m = 10. Из (10) следует, что десятая мода m = 10 (рис. 2 б ) – по следняя мода, при которой константа распространения (10) еще положительная. Но на рис. 6 видно, что эта мода не распространяется в ограниченном ГС-волноводе. Или, точнее говоря, распро стр аняется с потерями, то есть является вытекающей модой.

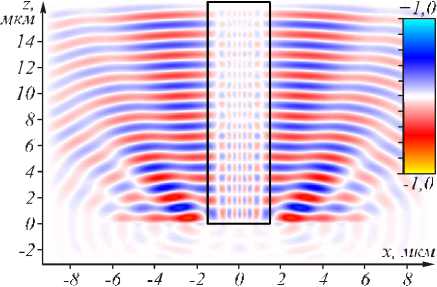
Рис. 6. Мгновенная картина р еальной части амплитуды напряженности электр ического поля, распространяющегося в ГС-волноводе (снизу вверх). На вход волновода при z = 0 подавалась ТЕ-мода (9) с номером m = 10

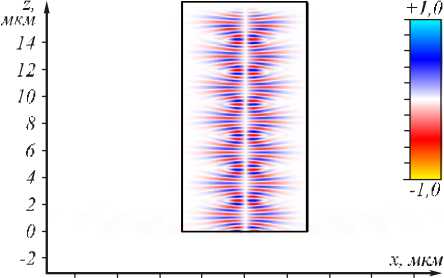
Результаты моделирования , демонстрирующие свойства периодического повторения (с периодом Тальбота (18)) светового поля с ТЕ-поляризаци ей в ГС-во лно воде, показаны на рис. 7. На этом рисунке показаны мгновенные распред еления реальной части амплитуды напряженности электрического поля , распространяющегося в ГС-волно воде (таком же, как на рис. 5). На вход волновода при z = 0 подавались ТЕ-моды (9) с номерами m = 3 (а) и m = 4 (б), но ширина которых была уменьшена в 3 раза a ’ = a /3. Уменьшение ширины моды, согласованной с во лноводо м, приводит к тому, что она уже перестает быть модой и распространяется как линейная комбинация мод (15). По это му при распространении такого светового поля наблюдается периодическое повторение поперечного сечения интенсивности с периодом Тальбота L = 2 π a = πλ = 4,87 мкм (рис. 7). На рис. 7 видно, что картины мод при m = 3 и m =4 имеют минимальный период, в два раза меньший, чем период Тальбо та L = 4,87 мкм. Это следует из того, что если в сумме (17) все m четны или нечетны, то период становится равен L = π a вместо 2 π a .

• 6.    Моделирование фокусировки света ГС-линзой

В этом разд еле приводятся результаты мод е-лирования субволновой фокусировки планарной ГС-линзой, ко торая представляет собой ограниченный по осям x и y кусок ГС-волновода c показателем преломления (1) при a = 2L’/ π, где L ’ – длина линзы .

б)

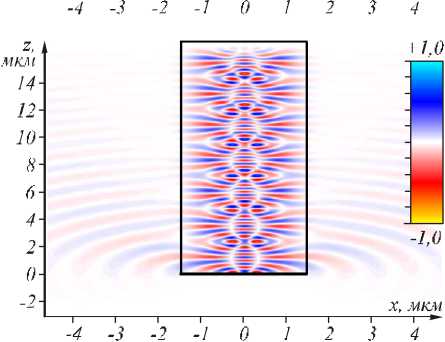
Рис. 7. Мгновенная картина реальной части амплитуд ы напряженности электри ческого поля, распространяющегося в ГС-волноводе (снизу вверх). На вход волновода при z = 0 подавались ТЕ-моды (9) с номерами m = 3 (а) и m = 4(б), но ширина котор ых была уменьшена в 3 раза: a’ = a/3

Расч ет производился с помо щью программы на языке программирования С++ [4], реализующей двумерный FDTD-метод разно стного решения системы уравнений Максв елла. Параметры моде-лиров ания: n = 3,1 – показатель преломления на оси линзы , ширина линзы 2 b = 5 мкм , длина линзы L’ = 2,2 мкм, длина волны λ = 1,55 мкм, число отсчетов на длину волны по пространственным переменным – 400, пад ающее излучение – плоская ТЕ-поляризованная волна. На рис. 8 показаны усредненное по времени распределение интенсивно -сти внутри ГС-линзы (а) и сечение этой интенсивно сти вдоль координаты x через фокус (б). При выбранных параметрах фокусное пятно на выходе ГС-линзы имеет минимальный размер FWHM = 0,131λ. Заметим, что такое фокусное пятно немного меньше, чем скалярный дифракционной предел в двумерном случае в среде, равный FWHM =0,44λ/ n = 0,14λ.

- X, мкм

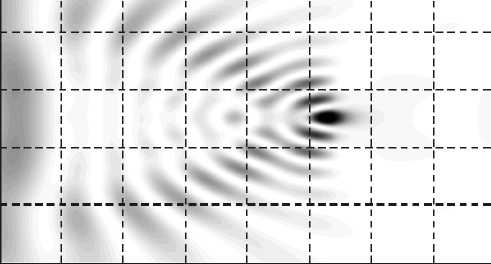
а) О 0,5    1,0   1,5   2,0   2,5   3,0 мкм

Рис. 8. Распределени е усредненной по времени интенсивности (в полутонах) внутри ГС-линзы (а) и сечение этой интенсивности по оси x через фокус (б)

На рис. 9 а приведен график зависимости ширины фокусного пятна от разбиения сетки отсчетов при расчете по методу FDTD в программе FullWave. Из него видно, что с увеличением разбиения N ширина фокуса почти перестает из меняться примерно со 100 отсчетов на длину волны, ширина фокуса при этом составляет FWHM = 0,131λ.

Для того чтобы показать, что приведенное значение ширины фокуса минимальное из возможных, ниже приводятся два графика, полученные в результате моделирования. На рис. 9 б , в показаны графики зависимости ширины фокуса в ГС-линзе по полуспаду интенсивности (в длинах волн) от величины показателя преломления n на оси линзы (б) при ширине линзы 2 b =5 мкм и длине L’ = 3 мкм и от длины линзы L ’ (в) при n =3,1 и ширине 2 b =5 мкм. Из рис. 9 видно, что минимальная ширина фокусного пятна достигается при n = 3,1, L’ =2,2 мкм, 2 b =5 мкм.

Заключение

В работе получены след ующие результаты:

– в явном виде выписаны ТЕ- и ТМ- моды для планарного ГС-волновода, в том числе волновода с «пьедесталом» (уравнения (9), (26), (33)); данные моды являются частным случаем более общих мод, распространяющихся в волноводах Эпштейна;

– получено выражение для периода Тальбота (или фокусного расстояния) для ТЕ-мод в планарном ГС-волноводе (уравнение (18)), и показано, что для ТМ-мод не возникает периодичность и нет фокусировки в ГС-волноводе; показано также, что в ГС-волноводе с «пьедесталом» для ТЕ-мод эффект Тальбота и фокусировка также отсутствуют ;

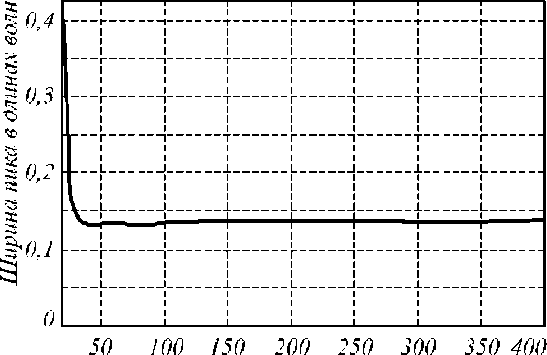
Число отсчетов сетки N на длину волны

а)

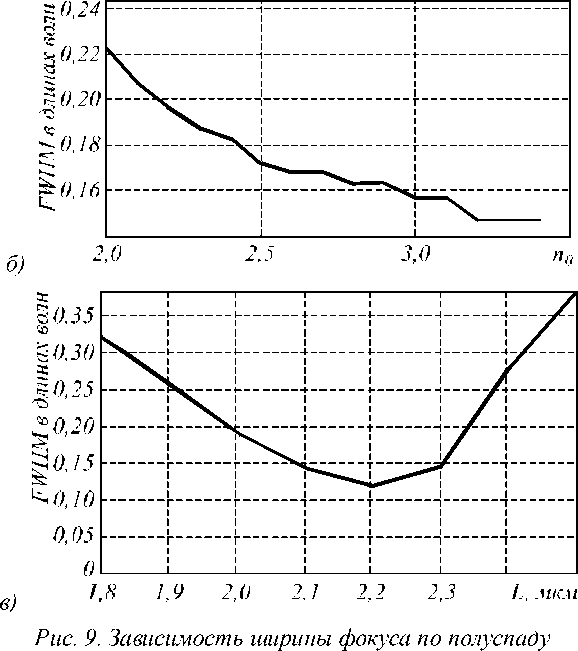
интенсивности FWHM (в длинах волн) в ГС-линзе от разбиения сетки при FDTD-методе расчета (а), от показа теля преломления на оп ти ческой оси (б) и от длины линзы (в)

– получены выр ажен ия для полной ширины по полуспаду интенсивности и нормированной интенсивности для основной ТЕ-моды в ГС-волноводе (уравнение (20)), и найдены параметры ГС-волновода, при которых ширина основной моды минимальна (рис. 3); миним альная ширина моды в кремниевом ГС-волноводе по полусп ад у интенсивности равна 0,11 от длины волны;

– с помощью моделиро вания программой FullWAVE показано модовое распространени е световых полей с начальными аналитически полученными амплитуд ами в ограниченных ГС-волноводах и периодическое повторение немодовых световых полей в волноводе с периодом Тальбота;

– с помощью моделирования также показано, что ГС-линза, являющаяся «куском» ГС-волновода, фокусирует плоскую ТЕ-волну в субволновое фокусное пятно шириной по полуспаду интенсивности 0,131 от длины волны. Это меньше, чем дифракционный предел в двумерной среде FWHM = 0,44 λ / n = 0,147 λ ( n = 3,1).

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9) и молодого кандидата наук (МК-64571.2010.2).