Моды шепчущей галереи для измерений поверхностного импеданса сверхпроводящих кристаллов

Основным способом изучения высокочастотных свойств сверхпроводников является измерение компонент их поверхностного импеданса Z = R + iX в абсолютных единицах (Om). Действительная часть импеданса, поверхностное сопротивление R, связана с потерями энергии электромагнитной волны при отражении от сверхпроводника и механизмом рассеяния нормальных носителей. Мнимая часть, реактанс X , характеризует отклик сверхпроводящих носителей. Измерив величины R и X , можно вычислить комплексную проводимость сверхпроводника.

Наиболее точными методами измерения импеданса являются резонансные методы. С их помощью производятся, например, измерения температурных зависимостей Z ( T ). Наилучшие результаты достигаются при помещении образцов в сверхпроводящие объёмные резонаторы [1], однако при использовании таких резонаторов невозможно исследовать магнитополевые свойства образца. Вместе с тем измерения зависимостей поверхностного импеданса от магнитного поля позволяют изучать структуру квазичастиц в ядрах вихрей, динамику вихревой решётки, а также температурную зависимость критических полей [2]. Обычно для этих целей используются медные объёмные резонаторы. Для повышения точности измерений импеданса во внешнем магнитном поле применяются диэлектрические резонаторы на низких модах [3]. В данной работе мы рассмотрели возможность использования высоких азимутальных мод цилиндрического сапфирового резонатора, так называемых мод «шепчущей галереи».

• II.    Резонансные методы температурных измерений поверхностного импеданса

Суть резонансных методов заключается в следующем [1]. При фиксированной температуре измеряются частота и добротность одной из мод электромагнитного резонатора. После этого в резонатор помещается сверхпроводящий кристалл небольшого размера (типичный размер 1 х 1 х 0,1 мм 3 ), что приводит к сдвигу частоты и изменению добротности резонатора. Если глубина скин-слоя меньше всех характерных размеров образца, то теория возмущений даёт следующую связь измеряемых величин с компонентами поверхностного импеданса образца:

R(T) = Г

Qm — Q o ( T ) / ,

X ( T ) = 2^r(f o (T) - f ( T ))+ X o .

f 0

Здесь f 0 , Q 0 — частота и добротность резонатора без образца; f , Q — частота и добротность резонатора с образцом, X 0 — аддитивная константа, T — температура образца. Значение гамма-фактора Г определяется геометрией образца и конфигурацией электромагнитного поля (модой) резонатора. Гамма-фактор характеризует чувствительность резонансной системы: чем меньше Г, тем выше чувствительность.

Когда температура образца ниже температуры сверхпроводящего перехода T _c , вклад самого образца в общие потери резонансной системы очень мал. Погрешность δR измерения действительной части импеданса в этом случае равна

δR = α ,

Q 0

где α — относительная погрешность измерения добротности. Отсюда следует, что существуют три пути повышения точности измерения R: увеличение добротности используемого резонатора, совершенствование метода прецизионных измерений добротности и уменьшение величины гамма-фактора образца. Следуя первому пути, мы применили в измерениях импеданса высокие моды сапфирового резонатора — моды «шепчущей галереи». При гелиевых температурах в миллиметровом диапазоне длин волн их добротность Q 0 может достигать 10 ⁸ , что значительно превышает значения добротностей объемных резонаторов из меди (Q 0 ∼ 10 ⁴ ) и ниобия (Q 0 ∼ 10 ⁶ ).

• III.    Сапфировый резонатор и электромагнитные поля «шепчущей галереи»

Использованный нами диэлектрический резонатор представляет собой цилиндр из монокристалла сапфира высотой 2,97 мм и диаметром 15,04 мм. Задача о распределении электромагнитного поля мод «шепчущей галереи» может быть приближённо решена с помощью метода частичных областей. Все компоненты электромагнитного поля резонатора отличны от нуля и периодически зависят от угла. Для измерения поверхностного импеданса предпочтительными являются HE _n,₁,₁ моды, вдоль оси симметрии Oz которых преобладает электрическое поле. Оптимальное расположение образца и силовые линии электромагнитного поля HE _n,₁,₁ мод показаны на рис. 1.

Во время эксперимента — измерений f (T ) и Q(T ) — температура сапфирового диска поддерживается постоянной и равной 4.2 К. Образец закрепляется на тонком сапфировом стержне на расстоянии 1 мм от боковой поверхности резонатора. Изменения температуры стержня, до- стигаемые с помощью удаленного нагревателя, точно соответствуют изменениям температуры образца. Внутренний объём резонаторного блока откачивается с помощью криогенного насоса для предотвращения нагрева сапфирового диска.

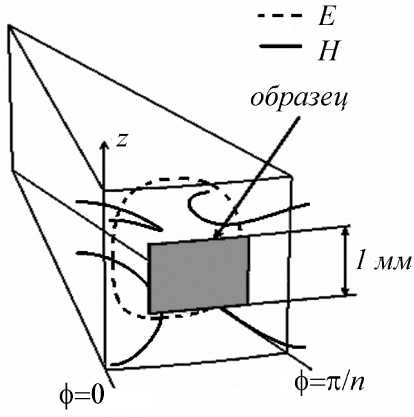
Рис. 1. Линии электромагнитного поля

HE _п, 1 , 1 мод ««шепчущей галереи» и оптимальное расположение образца

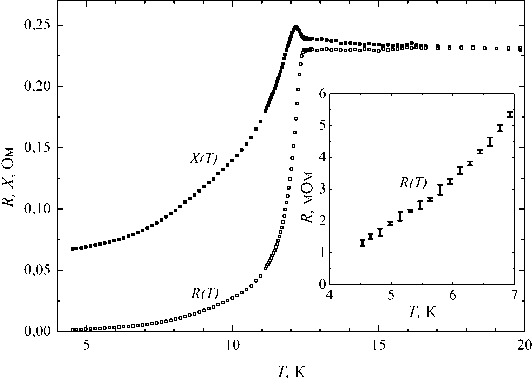
Рис. 2. Температурные зависимости компонент поверхностного импеданса кристалла V 3+x Si i_-x , измеренные на частоте 37 , 32 ГГц с помощью предлагаемой методики. На вставке показана низкотемпературная часть кривой R ( T )

Измерения импеданса кристаллов V3+xSi1-x. С целью проверки изложенного экспериментального метода были выполнены измерения температурных зависимостей поверхностного импеданса монокристаллов V3+xSii-x с содержанием кремния 24%. Измерения проводились на модах HEn,i,i с номерами n =11-14. Для примера приведены результаты, полученные на моде HE14,1,1, имеющей частоту 37,32 ГГц. Частота f0 и добротность Q0 = 6 • 106 резонансной системы на выбранной моде в отсутствие образца, но с сапфировым стержнем внутри не зависели от температуры стержня в пределах точности измерений, что связано со слабой температурной зависимостью диэлектрической проницаемости сапфира в области низких температур. Как видно из рис. 2, в нормальном состоянии образца при T > Тс ~ 12.5 K действительная и мнимая части импеданса равны: R(T) = X(T), что удовлетворяет критерию нормального скин-эффекта. При T < Tc на кривой X(T) наблюдается небольшой ««горб» («bump») — характерная особенность, присущая двухзонным сверхпроводникам. В области низких температур погрешность δR равна 200 мкОм. В целом, результаты, представленные на рис. 2, хорошо согласуются с измерениями импеданса монокристаллов V3+xSii-x на частоте 9,4 ГГц, выполненными с применением сверхпроводящего ниобиевого резонатора [4].

В заключение необходимо отметить недостатки рассматриваемой методики. Поскольку электромагнитное поле используемых мод весьма неоднородно, оказывается невозможным измерение поверхностного импеданса образцов в форме параллелепипеда, имеющих анизотропную проводимость. Поэтому рассматриваемый метод позволяет исследовать только изотропные вещества.