Моды шепчущей галереи в диэлектрическом цилиндре с круглым сечением

Субволновая фокусировка света (фокусировка в область с размерами меньшими длины волны) на микрочастицах и малых препятствиях, размеры которых, как правило, сравнимы с длиной волны, является относительно новой областью исследований, интерес к которой был вызван работой [1]. В [1] было продемонстрировано, что микросфера из диэлектрика позволяет фокусировать свет в достаточно узкую область (также называемую фотонной струёй). Если в область фотонной струи попадает наночастица, то рассеиваемое ею поле обнаруживает её. В [2] для фокусирования света в ближнем поле используются дифракционные решётки. В работе [3] рассматривается фокусировка на радиально-симметричных препятствиях, в [4] – на градиентной линзе. Ряд работ посвящён фокусировке с помощью многослойной микросферы [5], сфероидальной микросферы [6], двухслойной микросферы [7, 8], цилиндра [9– 11] и диска [12]. Основной областью применения острой фокусировки является зондирование и детектирование нанообъектов, так как острая фокусировка позволяет увеличить разрешение оптических детекторов частиц и микроскопов. В перечисленных выше микрообъектах могут быть возбуждены резонансы и соответствующие им моды. Оптические резонансы в частицах и микрообъектах применяются в высокочувствительных сенсорах и фильтрах [13]. Оптические резонансные моды обладают экстраординарной добротностью [14] и, следовательно, очень узкой спектральной шириной, что позволяет применять их в сверхчувствительных фильтрах. Оптические резонансы используются для получения субволновой фокусировки света, так как при возбуждении резонансных мод внутри частицы или компонента, которым производится фокусировка, поперечные размеры области фокусировки сокращаются [15 – 17].

-384.

В данной работе численно, на основе известного решения задачи дифракции света на цилиндре, исследуются моды шепчущей галереи и их влияние на субволновую фокусировку света. Данная работа является усовершенствованием результатов, полученных в [16], так как ширина фокуса получена с точностью до 0,001 длины волны. Также будет рассмотрена субволновая фокусировка и моды шепчущей галереи в двухслойном цилиндре. Будет показано, что учёт комплексного показателя преломления, то есть учёт поглощения материала, приводит к существенному ослаблению самих мод шепчущей галереи и их влияния на фокусировку света.

1.    Дифракция на однородном цилиндре

В [16, 17] продемонстрировано, как в однородном цилиндре можно добиться фокусировки TE-поляри-зованного излучения в область, более чем в два раза меньшую, чем дифракционный предел в двумерном случае (FWHM=0,44λ). Такой результат достигается при значениях радиуса, находящихся в некотором соотношении к длине волны, так, например, резонансная мода с номером 30 в цилиндре с показателем преломления n = 1,5875 усиливается при облучении монохроматическим светом (показатель преломления внешней среды n = 1), если соотношение между радиусом цилиндра и длиной волны составляет R = 3,4745041λ (ширина резонанса ΔR = 3,4×10–5λ). Значение данного отношения можно получить с произвольной точностью либо при помощи формул расчёта приближённого значения в [17], либо при помощи оптимизационного алгоритма. При условии, что это соотношение выполняется, на границе цилиндра образуются чередующиеся максимумы и минимумы интенсивности. Отдельный максимум на теневой стороне цилиндра на оптической оси можно рассматривать как фокусное пятно, формируемое цилиндром. Для мод с номерами 25^65 рассчитаны значения FWHM (размера ширины фокуса по полуспаду интен- сивности в направлении, перпендикулярном распространению света) в длинах волн λ с точностью до третьего знака после запятой (рис. 1). Интенсивность рассчитывается как квадрат модуля амплитуды напряжённости электрического поля. На рис . 1 изображены три графика, полученные для трёх значений показателя преломления: n = 1,5875 (полиэстер при длине волны гелий-неонового лазера λ =632,8 нм), n = 1,6010 (полиэстер при длине волны аргонового лазера λ =514 нм), n = 1,6117 (полиэстер при длине волны аргонового лазера λ =488 нм) [18].

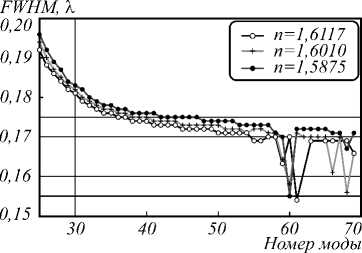
Рис. 1. Поперечные размеры фокусного пятна по полуспаду интенсивности света в зависимости от номера возбуждаемой в цилиндре моды

Следует отметить, что все значения FWHM на рисунке получены из аналитического решения задачи дифракции плоской монохроматической ТЕ-вол-ны на однородном диэлектрическом цилиндре. Во-первых, из рис. 1 следует, что минимальный размер фокуса равен (0,155 ± 0,001) λ. Этот минимальный фокус получается при фокусировке моды с номером 60 ( n = 1,5875) для цилиндра с радиусом R =6,63186178877λ (Δ R = 4,0×10^–10λ). Во-вторых, интерес представляет сама резонансная мода с номером 60, при которой на границе цилиндра образуется пятно с минимальным поперечным размером. На рис. 1 для этой моды кривая FWHM имеет резкий локальный минимум. Двумерное распределение интенсивности вблизи фокуса для данного случая (мода с номером 60) показано на рис. 2.

На рис. 2 видно, что вблизи маленького центрального пятна (левый вертикальный белый отрезок), образовавшегося на границе цилиндра, также формируются три пятна, одно из которых представляет фотонную нанострую, а два других – лепестки, образовавшиеся в результате интерференции проходящего излучения и моды, образуемой в цилиндре. Интенсивность в центральном максимуме в 50 раз превышает интенсивность падающего света, однако интенсивность соседних лепестков превосходит её в два раза (рис. 3 а ). Интенсивность в максимуме фотонной струи (правый вертикальный белый отрезок) более чем в 2 раза меньше (рис. 3 б ). Фотонная струя – это область второго вдоль оптической оси фокуса, максимум которого формируется на расстоянии 0,87λ от поверхности цилиндра и имеет ширину 0,44λ и глубину 2λ.

Для сравнения на рис. 4 приведена картина интенсивности, которая формируется при резонансе моды с номером 30 (n = 1,5875), R =3,4745041λ. Интенсивность на границе цилиндра в 1400 раз больше, чем интенсивность падающего света. При резонансе 30 моды тоже образуется фотонная наноструя, которую не видно на рис. 4 из-за того, что её интенсивность в максимуме всего в 10 раз превосходит интенсивность падающего света.

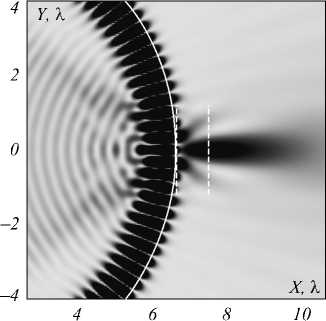
Рис. 2. Двумерное негативное распределение интенсивности света вблизи границы цилиндра, внутри которого формируется мода шепчущей галереи с номером 60

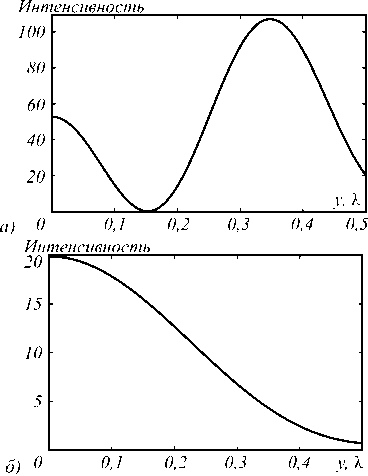
Рис. 3. Распределение интенсивности в поперечном сечении на границе цилиндра (а) и на расстоянии 0,86λ от поверхности (б) от центра симметрии перпендикулярно оптической оси

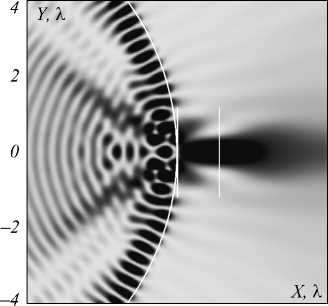
На рис. 1 некоторые точки пропущены. Это связанно с тем, что не при всех резонансах образуется пятно на границе цилиндра. Например, картина распределения интенсивности моды 62 ( n = 1,6117), R = 6,7391161λ (Δ R = 2×10^–11λ) представлена на рис. 5.

При резонансе на поверхности на оптической оси не образуется фокус (левая пунктирная белая линия на рис. 5). Это говорит о том, что не все моды с номерами больше 50 являются устойчивыми, то есть не все удерживаются внутри цилиндра так же хорошо, как, например, мода с номером 30 на рис. 4. Об этом говорит в первую очередь меньшее значение максимальной интенсивности на границе цилиндра: интенсивность в лепестках моды на рис. 5 много меньше, чем интенсивность моды на рис. 4, и сравнима с интенсивностью в фотонной струе (правая пунктирная вертикальная белая линия на рис. 5).

2         3        4        5

Рис. 4. Двумерное негативное распределение интенсивности света вблизи границы цилиндра, внутри которого формируется мода шепчущей галереи с номером 30

4       6       8       10

Рис. 5. Двумерное негативное распределение интенсивности света вблизи границы цилиндра, внутри которого формируется мода шепчущей галереи с номером 62

2.    Дифракция на двухслойном цилиндре

В предыдущем параграфе показано, что минимальный размер фокуса вблизи поверхности резонансного однородного цилиндра равен 0,155Х. Для мод с номерами 30 ^ 50 минимальное фокусное пятно имеет поперечный размер немного больше -(0,175 ±0,05)X. Конкретное значение радиуса и показателя преломления может быть выбрано в зависимости от необходимой величины чувствительности резонанса и его добротности.

Альтернативным вариантом фокусировки однородным цилиндром может служить фокусировка двухслойным диэлектрическим цилиндром. В двухслойном цилиндре, внутренний слой которого будем называть ядром, а внешний - оболочкой, можно воспроизвести два типа резонанса в зависимости от соотношения показателей преломления оболочки и ядра. Если ядро имеет больший показатель преломления, чем оболочка, будут получены картины, полностью аналогичные картинам интенсивности в предыдущей части, поэтому они не представляют интереса (ещё и потому, что фокус будет образовываться в оболочке, а не снаружи цилиндра). Если же оболочка имеет показатель преломления больший, чем ядро, то внутри оболочки также может образовываться стоячая волна за счёт полного внутреннего отражения излучения от внутренних границ оболочки.

Решение задачи дифракции на двухслойном цилиндре с круглым сечением (как и на цилиндре с произвольным количеством слоёв) основывается на использовании разложения в ряд по цилиндрическим функциям [18], где напряжённость электрического поля может быть выражена следующим образом (TE-поляризация):

+^

E ₂( r , ф ) = £ z ^j C j [ J j (kr ) + ^Н™(kr ) ] e '^{j ф} , (1) ^j =^-™

+^

E 1 ( r , ф ) = £ i^j C j [ A j J j (k^ r ) + B j Y j ( knr ) ] e '^{j ф} , (2) ^j =^-™

E 0 ( r , ф ) = £ V C j G j J j( kn 0 r ) e j ^ф .                 (3)

^j =^-™

Здесь E0, E1, E2 - напряжённость электрического поля в ядре, оболочке и снаружи цилиндра соответственно; Jj, Yj, Hj(1) - функции Бесселя, Неймана и Хан-келя первого рода, k - волновое число в вакууме; n 1, n0 - показатели преломления оболочки и ядра (показатель преломления среды n = 1); Cj - коэффициенты разложения поля падающего излучения, равные 1 в случае падения на цилиндр плоской монохроматической волны. Коэффициенты разложения Fj, Aj, Bj, Gj связываются в СЛАУ, полученную из граничных условий для поля на границе раздела между слоями ци- линдра:

Lj

f j

A j

G

V j 2

f ^- J j ^{( k}r ) ) - kJ ‘ ( ^kr )

0 J где Lj представляет собой следующую матрицу:

^f H।kr)    -J j ⁽ kniri)

kH j ^1)- ( k ^) - kn^J ‘ ( kn^rD

⁰          J j ^{( k}n r ₀)

_v 0        k^J ‘ ( k^r ₀)

- Y j ( kn r )          0

- kn1Y ' ( kn r )        0

Y j ⁽ fan ^r 0 )       ^{- J} j ^{( kn} 0 ^r 0 )

kn₁Y ' ( kn r ₀) - kn ₀ J ‘ ( kn ₀ r ₀) ₂

В данных обозначениях r 0 – радиус ядра цилиндра, а r 1 – радиус оболочки. Полученные в результате решения СЛАУ коэффициенты используются для построения распределения напряжённости электрического поля по формулам (1), (2) и (3).

Руководствуясь теми же принципами, что и при фокусировке однородным цилиндром, в качестве материалов следует выбрать кварцевое стекло n 0 = 1,4570 и полиэстер n 1 = 1,5875 при длине волны гелий-неонового лазера. Меньший показатель преломления в ядре позволит получить резонанс в оболочке за счёт внутреннего отражения от границы между ядром и оболочкой.

Благодаря дополнительной степени свободы (радиус ядра), для любого фиксированного радиуса оболочки существует радиус ядра, при котором детерминант матрицы (5) достигает минимального значения. Если детерминант близок к нулю, то будет наблюдаться резонанс. Однако гораздо более наглядным показателем, указывающим наличие резонанса, является значение интенсивности света на границе цилиндра. На рис. 6 показаны несколько зависимостей интенсивности света на границе цилиндра от радиуса.

Относительная интенсивность света

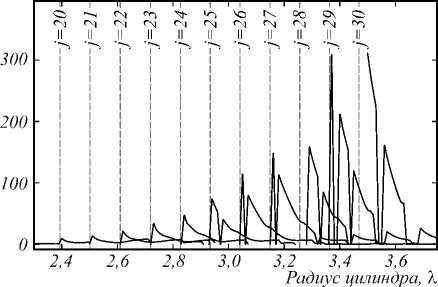
Рис. 6. Относительная интенсивность света на границе цилиндра для мод различных номеров и различных значений радиуса r1: для каждого фиксированного j и r1 определяется r2 по минимуму абсолютного значения детерминанта (5)

Рис. 6 состоит из нескольких графиков, показывающих зависимость интенсивности света на границе цилиндра от радиуса r 1 , при условии, что радиус ядра r 0 подбирается таким образом, что достигается минимум детерминанта (5). Моды, изображённые на рис. 6, имеют номера от 20 до 30. Из данного графика можно сделать вывод, что при значениях радиуса оболочки меньше резонансного получить яркое и узкое пятно в фокусе не представляется возможным. Мода с произвольным номером может быть получена при различных радиусах оболочки при условии, что этот радиус больше, чем соответствующий резонансный радиус однородного цилиндра. В зависимости от радиуса цилиндра изменяются параметры фокусного пятна. Так, на рис. 7 представлена зависимость интенсивности в максимуме и поперечный размер фокуса, образуемого на границе двухслойного цилиндра, в котором возбуждается мода с номером 25.

О

а)

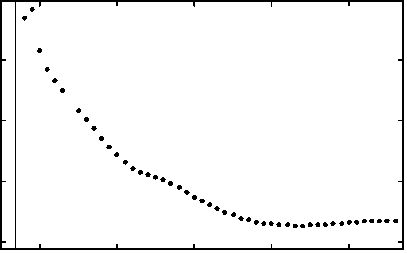
Относительная интенсивность света 80

2,95     3,00     3,05     3,10     3,15

Paduvc цилиндра, X

FWHM, X

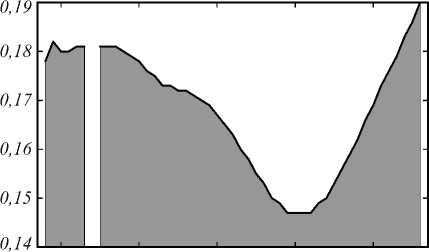
2,95     3,00     3,05     3,10     3,15

Радиус цилиндра, X

Рис. 7. Интенсивность (а) и поперечные размеры по полуспаду интенсивности (б) фокусного пятна на границе двухслойного цилиндра из полиэстера при резонансе моды с номером 25

Следует заметить, что, так же как и фокусировка однородным цилиндром, фокусировка двухслойным цилиндром не всегда позволяет получить пятно на границе цилиндра при заданных параметрах (аналогично рис. 5). Поэтому на рис. 7 б для промежутка r 1 ∈ [2,965; 2,975] значения FWHM пропущены. При различных значениях радиуса можно найти баланс между интенсивностью в центральном максимуме и размером фокуса. Так, если выбрать радиус оболочки r 1 = 3,03λ, то FWHM = 0,172λ, а интенсивность будет превосходить интенсивность падающего света в 20 раз. А при r 1 = 3,05λ интенсивность будет уже лишь в 15 раз превосходить интенсивность падающего света, но FWHM = 0,167λ. Следует заметить, что интенсивность соседних максимумов превосходит интенсивность падающего света в 50 раз, и центральный максимум при этом является существенно более слабым.

3.    Влияние поглощения на резонансную фокусировку

В предыдущих параграфах картины интенсивности, которые были использованы для определения FWHM, рассчитываются в случае идеальных материалов без поглощения. Поглощение материалов можно учесть в аналитическом решении, чтобы проанализировать, во-первых, как сильно резонансы чувствительны к поглощению материалов, а во-вторых, какого минимального размера фокуса можно добиться для материала с показателем поглощения, равным показателю поглощения реального материала.

К сожалению, измерению поглощения в полиэстере посвящено малое число работ. Можно выделить статью [19], которая посвящена исследованию оптических свойств полиэстера в инфракрасном диапазоне, и статью [20], посвящённую описанию комплексной части показателя преломления полиэстера в диапазоне от видимого до рентгеновского излучения. Из [19, 20] можно лишь оценить верхнюю границу значения поглощения материала (мнимая часть комплексного показателя преломления), составляющую приблизительно (1,0 ^ 2,5)х10^-3. В [21] проведено сравнение оптических свойств полиэстера, легированного йодом, с полиэстером без модификаций на примере оптических плёнок. Для интересующей длины волны (длина волны гелий-неонового лазера – 632,54 нм) мнимая часть показателя преломления составила (1,2 ^ 1,1)х10^-3.

Коэффициент поглощения может быть значительно уменьшен, если использовать легированный материал. В [22] представлены данные для спектра видимого света полиэстера, облучённого ионами Ar++ и H+. При длине волны гелий-неонового лазера мнимая часть показателя преломления достигает значения k = 2,73×10^–7, после облучения полиэстера ионами H+ с энергией 200 кэв (минимальной концентрации). Аналогично k = 2,54×10^–5 при облучении ионами Ar++ с энергией 400 кэв.

Чтобы оценить, насколько фокусное пятно чувствительно к поглощению материала и при каких условиях резонансная мода будет воспроизводиться, получены зависимости интенсивности в максимуме фокуса. Так, для моды с номером 60 зависимость представлена на рис. 8, а для моды с номером 30 – на рис. 9.

Интенсивность света на границе цилиндра

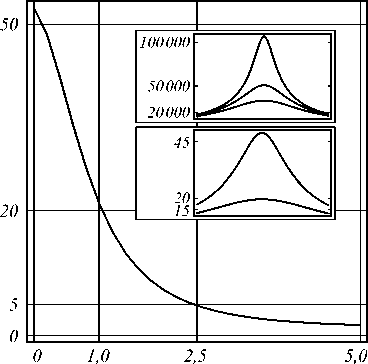
Мнимая часть показателя преломления, к, МО-8

Рис. 8. Максимальная интенсивность на оптической оси на границе цилиндра, в котором возбуждается мода с номером 60; на вставках изображены зависимости коэффициента моды в разложении по цилиндрическим функциям вблизи резонансного значения при различных значениях показателя преломления, сверху вниз: k = 0, k = 0,5×10–11, k = 10–11, k = 10–8, k = 2,5×10–8

Из рис. 8 видно, что распределение интенсивности, изображённое на рис. 2, невозможно получить при значениях поглощения, близких к полиэстеру. Уже при k = 2,5×10–8 интенсивность в максимуме на границе цилиндра падает на порядок, а при больших значениях фокусное пятно разрушается, так как разница между первым минимумом интерференции и максимумом становится едва различимой. Сам же резонанс при наличии поглощения остаётся, но проявляется гораздо хуже: на вставке на рис. 8 и рис. 9 видно, что максимум коэффициента в разложении по модам не сдвигается, но для 60-й моды падает на пять порядков уже при k = 10–8. Таким образом, фокус для моды с номером 60 невозможно получить даже на специальных материалах, которые были рассмотрены выше. Мода с номером 30 может быть получена при значении коэффициента поглощения вплоть до k = 1×10–5, а минимальный размер фокуса FWHM=0,18λ получается для коэффициента поглощения k =2,73×10–7.

Интенсивность света на границе цилиндра

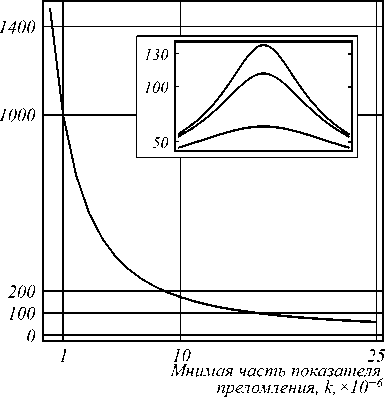
Рис. 9. Максимальная интенсивность на оптической оси на границе цилиндра, в котором возбуждается мода с номером 30; на вставке представлена зависимость коэффициента моды в разложении по цилиндрическим функциям при k = 0, k = 10–6, k = 5×10–6

Зависимость FWHM (30-я мода) от коэффициента поглощения представлена на рис. 10, из которого видно, что FWHM увеличивается при увеличении поглощения материала.

Благодаря поглощению мода становится менее устойчивой в цилиндре и вытекает из него быстрее, однако это не всегда приводит к увеличению FWHM на границе цилиндра. Зависимость, аналогичная представленной на рис. 1, но для цилиндров с k = 2,73×10^–7, изображена на рис. 11.

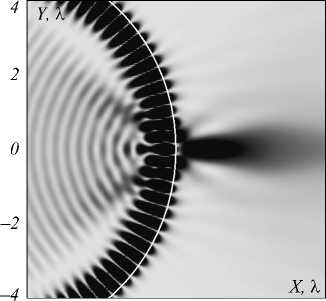
Из рисунка следует, что для мод 40 и выше увеличение поглощения приводит к уменьшению размеров максимума на границе. Например, распределение интенсивности при возбуждении моды с номером 48 изображено на рис. 12. Размер едва выступающего на границе цилиндра на оптической оси максимума интенсивности составляет всего 0,138λ. Следует обратить внимание на то, что распределение интенсивности на рис. 12 практически полностью аналогично представленному на рис. 2, хотя оно получено при нулевом значении поглощения.

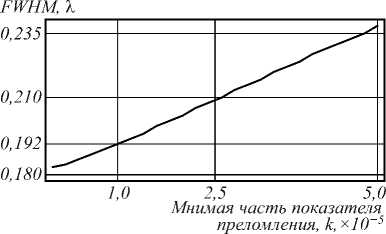
Рис. 10. FWHM в зависимости от мнимой части показателя преломления полиэстера с действительной частью n = 1,5875 при резонансе моды 30 в однородном цилиндре

Рис. 11. FWHM в зависимости от номера возбуждаемой моды при k = 2,73×10–7

2        4        6        8

Рис. 12. Двумерное негативное распределение интенсивности света вблизи границы цилиндра с показателем поглощения k = 2,73×10–7, внутри которого формируется мода шепчущей галереи с номером 48

Заключение

В работе были получены следующие результаты. Численно с высокой точностью определён минимальный размер фокусного пятна при дифракции плоской волны ТЕ-поляризации на однородном идеальном цилиндре из полиэстера с резонансным радиусом: он равен FWHM = (0,155 ±0,001) λ. При фокусировке плоской волны двухслойным цилиндром можно получить фокус меньшего размера FWHM = (0,147 ±0,001) λ, однако интенсивность максимума будет всего в 5,5 раз превосходить интенсивность падающего излучения. Учёт поглощения в материале, с одной стороны, мешает острой фокусировке света, а с другой – позволяет получить меньшие размеры фокуса: так, фокус с размером FWHM = 0,138λ был получен при резонансе моды 48 в цилиндре из полиэстера с n + ik =1,5875+ i ·2,73×10^–7.

Работа выполнена при поддержке гранта Российского научного фонда № 17-19-01186.