Молекулярно-динамическое моделирование влияния двухосных деформаций на растворимость водорода в ОЦК-железе с использованием ЕАМ-потенциалов

Комплекс негативных воздействий водорода на металл называют водородной деградацией [1–2]. Процессы водородной деградации существенно зависят от особенностей диффузии и растворимости водорода в конкретных материалах. Современный обзор исследований влияния таких особенностей можно найти в [3–5].

Многие промышленные изделия при изготовлении сохраняют существенные остаточные напряжения (сварные трубы, сварные швы, несущие балки). В этом случае особую ценность для прогнозирования процессов деградации имеют зависимости растворимости и коэффициента диффузии водорода от температуры образца и напряжений, приложенных к образцу. Однако долгое время подобные исследования проводились отрывочно, и построение теории влияния напряжений на поведение водорода в металлах далеко от завершения.

Экспериментально подтверждено [5], что в разбавленных твердых растворах водорода в ОЦК-железе атомы водорода при комнатной температуре располагаются в тетраэдрических порах решетки железа. Однако в экспериментальных работах с принудительным насыщением образца водородом с помощью электрохимических методов или водородной атмосферы с повышенным давлением (см. обзор [6]) было показано, что часть атомов водорода оказывается в октаэдрических порах, причем их количество увеличивается с ростом температуры. Результаты ряда экспериментов (см. [7] и ли- тературу, приведенную в источнике) показали, что в присутствии растягивающих напряжений эта доля может быть увеличена посредством локальной кластеризации водорода. Кластеры имеют форму плоскостей с периодом, совпадающим с параметром ОЦК-железа [7]. Этот эффект был обнаружен и в отсутствие внешних растягивающих напряжений. Его связывают с увеличением концентрации водорода. При повышении температуры происходит рост кластеров, а при температурах выше 500 К кластеры распадаются (см. [8, 9]). Недавние результаты моделирования зависимости энергии растворения водорода от одноосной, двухосной и трехосной деформаций с использованием первопринципных методов [10] показали возможность увеличения доли растворенного в октапорах водорода при приложении двухосных напряжений к суперячейке. Было показано, что при относительном двухосном сжатии образца более чем на 4 % и растяжении более чем на 6 % водород начинает переходить из тетрапор в октапоры.

В связи с этим возникает вопрос о влиянии данного явления на механизмы диффузии водорода в ОЦК-железе, подвергнутом деформации. Поскольку экспериментальное изучение степени относительного заполнения окта- и тетрапор ОЦК-железа является достаточно сложным, то представляется разумным привлечь для рассмотрения данного вопроса методы прямого компьютерного моделирования. В литературе имеется множество данных [2–6] о коэффициенте диффузии водорода, полученных как из эксперимента, так и методами компьютерного моделирования, которые отличаются на порядки. Для внесения дополнительной ясности в исследуемый вопрос необходимо использовать методики моделирования диффузионных процессов. Они требуют рассмотрения системы с большим числом атомов (порядка ~ 103 ). Поэтому подходящей методикой является метод молекулярной динамики. При его использовании встает вопрос о модели межчастичного взаимодействия. В настоящее время наиболее точными потенциалами для моделирования считаются потенциалы погруженного атома (ЕАМ-потенциалы), позволяющие качественно учитывать влияние окружения на межчастичные взаимодействия. Для молекулярно-динамического моделирования системы Fe–H в настоящее временя разработаны EAM-потенциалы (Руда, Вен, Картер) и MEAM-потенциал Ли (см. ссылки в [11]). В работах Пакстона и Чу-Чун Фу [12, 13] показано, что EAM-потенциалы Картер [11] приводят к результатам, хорошо согласующимся с рядом данных натурного и компьютерного эксперимента. В частности, EAM-потенциалы Картер хорошо воспроизводят диффузионные барьеры и энергию растворения водорода в чистом, бездефектном ОЦК-железе. В своей работе Картер представила четыре типа потенциалов. Однако из-за того, что тестирование потенциалов проводилось для ограниченного набора свойств системы Fe–H (зависимость диффузионных барьеров и энергии растворения водорода от упругих деформаций, энергия связи водорода и вакансий, энергия связи водорода и ядра винтовой дислокации), выделить наиболее точный из построенных потенциалов не удалось. Поэтому в данной работе мы использовали все 4 указанных потенциала (A, B, A’, B’) с целью определения оптимального для моделирования процесса диффузии водорода в ОЦК-железе.

В этой работе мы проводим тестирование потенциалов Картер на воспроизведение основных энергетических характеристик, хорошо изученных методами первопринципного моделирования, а именно: энергии растворения водорода и величины диффузионных барьеров. После этого проведем исследование зависимости энергии растворения атомов водорода от величины двухосной деформации. Результаты моделирования сопоставляются с аналогичными результатами, полученными в статьях [10] и [12, 13].

Методика моделирования

Для получения результатов использовалась реализация метода молекулярной динамики в программном пакете LAMMPS [14]. В работе тестируются 4 межатомных потенциала Картер. Воспроизведение энергетических параметров проводилось на системе с суперячейкой 10x10x10 атомов железа и одним атомом водорода. Минимиза- ция потенциальной энергии и объема структур проводилась методом сопряженных градиентов с точностью 10-25 по энергиям и по силам. Энергия и сила измерялись в электронвольтах (эВ) и элек-тронвольтах/ангстрем (эВ/Å). При расчете энергий растворения водорода в заданной конфигурации при фиксированном атоме водорода на нем обнулялась сила.

Перед проведением численных экспериментов один атом водорода помещался в суперячейку при 0 К, после чего проводилась минимизация полной энергии системы и действующих на атомы сил. Данная процедура показала, что предпочтительной позицией для водорода являются тетраэдрические поры, что согласуется с наблюдаемой ранее картиной в экспериментах и при моделировании системы ОЦК-Fe–H [5].

Ключевую роль при моделировании динамических характеристик системы Fe–H играет воспроизведение диффузионных барьеров и энергий активации водорода. Для него возможны три направления перескока: октапора – тетрапора – октапора ( O – T – O ), тетрапора – октапора – тетрапора ( T – O – T ) и тетрапора – локальный минимум – тетрапора ( T – S – T ) (рис. 1). В работе [6] было показано, что влияние на коэффициент диффузии имеют только переходы T – S – T , T – O – T . Соответствующие им энергии активации равны изменению энтальпии процесса перескока водорода

A E = A H = A U + p А V , где A U - изменение потенциальной энергии; p - давление; А V - изменение объема системы. В работе [15] при помощи ab initio методов были рассчитаны значения A U в выделенных направлениях [100] _O ( T – O – T ) и [101] _t ( T – S – T ) (рис. 1) как функция смещения вдоль этих направлений. Аналогичный, более свежий расчет был проведен в работе [13]. В настоящей статье с целью тестирования ЕАМ-потенциалов мы провели аналогичные расчеты методом МД-моделирования в пакете LAMMPS.

Для воспроизведения энергий активации и потенциального барьера при моделировании процесса диффузии достаточно рассчитать потенциальную энергию системы в точках S , T , O после релаксации. Моделирование системы проводилось при фиксированном положении водорода. Энергетические барьеры рассчитывались по формулам:

A U t - _s - T = E relax ( Fe n H( S ) ) - E relax ( Fe N H(T ) ) ;

A U t - O - T = E relax ( Fe N H( O ) ) - E relax ( Fe N H( T ) ) , где A U_T - _S - _T и A U_T - _O - _T - потенциальные барьеры перехода ( T - S - T ) и ( T - O - T) ; E_relax ( Fe N H( S ) ) , E relax ( Fe N ^{H( T} ) ) , E relax ( Fe N ^{H( O} ) ) ^{- соответст} вующие энергии системы с водородом, находящимся в точках S , T , O , после минимизации энергии и объема. Вместе с тем была рассчитана энер-

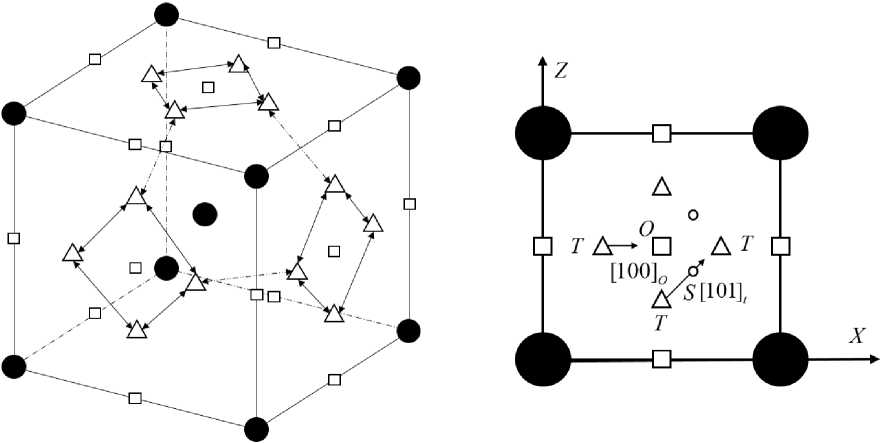
Рис. 1. Особые точки потенциальной энергии взаимодействия Fe–H. Квадраты – октапоры, треугольники – тетрапоры, черные незакрашенные точки – локальный минимум между тетрапорами

Результаты воспроизведения энергетических характеристик системы Fe–H

Характеристика	DFT	Эксп. [16]	DFT+MD [13]	Потенциалы A , B		Потенциалы A’ , B’
E sol , эВ	0,23 [13]	0,30	–	0,2365	0,2472	0,2746	0,2514
∆ UT - S - T , эВ	0,042 [15] 0,044 [13]	–	0,040	0,0443	0,0539	0,0432	0,0643
∆ UT - O - T , эВ	0,035 [13]	–	0,049	0,0561	0,0491	0,0625	0,0741
∆ U T - S - T - ∆ U T - O - T , эВ	0,009 [13]	–	0,009	–0,0118	0,0048	–0,0193	–0,0098

гия растворения водорода (водород располагался в тетраэдрической поре)

E sol = E (Fe N H) - E (Fe N ) - 0, 5 E (H 2 ) , где для энергии связи молекулы водорода E (H₂) принято значение –4,651 эВ. Результаты расчета представлены в таблице.

Проведенное тестирование показывает, что только потенциал B хорошо воспроизводит разницу ∆ U между барьерами и величину самих барьеров. Остальные результаты моделирования ∆ U_{T - O - T} и ∆ U_{T - S - T} неплохо согласуются с результатами [13, 15], но приводят к неверным результатам для величины ∆ U_{T - S - T} -∆ U_{T - O - T} . В связи с этим дальнейшее моделирование проводилось с использованием потенциала B как наиболее точного.

Влияние деформаций на энергию растворения водорода

Особую важность в воспроизведении перехода из тетрапоры в октапору имеет зависимость энергии растворения водорода от двухосной деформации. Энергия растворенного водорода в де- формированном образце Eεdissol рассчитывалась по формуле dissol

Eε    = Eε,FeN H - Eε,FeN , где Eε,Fe H – энергия системы в присутствии напряжений с водородом; Eε,Fe – энергия системы в присутствии напряжений без водорода.

Для рассмотрения различающихся конфигураций водорода в матрице ОЦК-железа требуется провести классификацию октапор и тетрапор. Любая занятая водородом октапора вызывает максимальное искажение решетки в направлении малой диагонали октаэдра. Эти искажения могут быть направлены по осям x , y , z или [100], [010], [001]. По отношению к ним разделим октапоры на три типа: октапоры x -, y -, z -типа. В то же время заполненная водородом тетрапора вызывает искажения решетки по двум ребрам тетраэдра. Среди всех возможных искажений, вызываемых водородом, находящимся в тетрапоре, неэквивалентных всего три: xy , xz , yz . Соответственно, будем различать тетрапоры xy -, xz -, yz -типа.

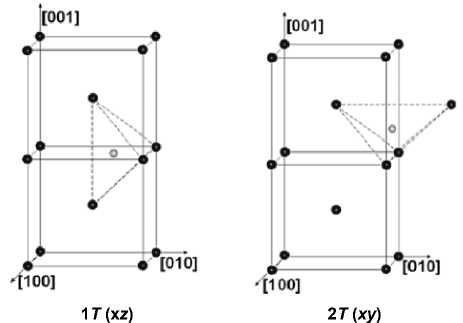
Рис. 2. Используемые конфигурации (черные точки – атомы железа, белые – атом водорода)

1 O ( z )

2 O ( x )

Проведем деформацию образца по направлениям [100] и [010] одновременно. Нагрузки были выбраны так, чтобы результирующее относительное удлинение (сжатие) образца находилось в области 0,9÷1,1 параметра суперячейки. Из-за наличия симметрии в структуре чистого ОЦК-железа нам достаточно рассмотреть среди октапор октапоры x - и z -типа, среди тетрапор – xy - и xz -типа (см. рис. 2)

Результаты расчета представлены на рис. 3 и 4. Значения получены после проведения минимизации полной энергии системы для атома водорода во всех направлениях и для атомов железа по направлению [001].

При отсутствии напряжения диффузия водорода в бездефектном ОЦК-железе при комнатной температуре протекает по тетрапорам [5]. При двухосном сжатии по направлениям [100] и [010] менее чем на 7 % энергия растворения водорода в тетрапорах растет быстрее, чем энергия растворения водорода в октапорах типа 1 O . В этой области деформаций при моделировании обнаруживается тенденция к переходу водорода в октапору типа 1 О . Она проявляется в виде смещения равновесного положения водорода из тетрапоры типа 1 T в сторону октапоры 1 O по прямой линии. При сжатии более 7 % разница в энергии растворения водорода между октапорами типа 1 O и тетрапорами 1 T становится существенной. В этой области происходит переход водорода из тетрапоры 1 T в октапору 1 O . В области растяжений менее 8 % у водорода в тетрапоре типа 2 T появляется смещение атома водорода в сторону октапоры типа 2 O . Растяжения более 8 % приводят к переходу водорода в тетрапоре 2 T в октапору 2 O .

Полученные нами результаты позволяют высказать следующее положение. Предположим, что при комнатной температуре в ОЦК-железе возможно локальное повышение концентрации водорода в порах xz-типа. Индуцированные водородом в тетрапорах xz-типа двухосные растяжения складываются в конструктивные локальные двухосные деформации решетки по направлениям x, z. В этом случае положение xz-тетрапор смещается в сторону z-октапор. При критических локальных концентрациях водорода, вызывающего деформации xz-типа более 8 %, начнет проявляться механизм перехода водорода из xz-тетрапор в z-октапоры. После перехода из равновесного положения вблизи xz-тетрапоры в z-октапору водород вызывает максимальные искажения вдоль оси z. Это искажение конструктивно складывается с другими искажениями в направлении z, вызванными водородом в xz-тетрапорах. Такие конструктивные искажения активируют механизм перехода для ближайших атомов водорода, находящихся в xz-тетрапорах, в z-октапоры. Для каждого атома водорода, находящегося в октапоре z-типа, энергия в ближайших тетрапорах xz-, yz-типа выше, чем в октапоре. Следовательно, для водорода в z-октапорах увеличивается длина диффузионного перескока. Она активируется при определенных температурах. При температурах ниже этого барьера часть локального скопления атомов водорода запирается в z-октапорах. Такой переход водорода из xz-тетрапоры в z-октапоры аналогичен попаданию его в высокоэнергичные ловушки, создающие вокруг себя такие же ловушки для водорода. Этот процесс со временем может привести к локальному скоплению водорода в z-октапорах – его кластеризации. Кластеры будут иметь периодическую структуру с периодом, соответствующим периоду решетки ОЦК-железа.

Аналогичную характеристику кластеру дают в работе [7]. Образованные кластеры с конструктивным искажением решетки вдоль оси z могут привести к понижению пороговой деформации, необходимой для фазового перехода железа из ОЦК- в ГЦК-фазу. Влияние водорода на этот переход экспериментально подтверждено [3]. Особенно важно то, что кластеризация водорода при двухосных деформациях более 10 % может привести к образованию микротрещин и дислокаций в окрестности кластера, что понизит предел текучести.

Обсуждение результатов и выводы

Результаты проведенных численных экспериментов подтверждают, что разработанные EAM-потенциалы Картер хорошо воспроизводят основные энергетические характеристики: энергию растворения водорода, величину потенциальных барьеров, разницу между ними. В присутствии двухосных деформаций наблюдается хорошее согласие результатов моделирования зависимости энергии растворения с использованием потенциала B в области двухосного сжатия с результатами [10]. Также результаты проведенных численных экспериментов показали, что потенциал B пригоден для воспроизведения механизма перехода водорода из тетрапоры в октапору. Полученные результаты согласуются с результатами расчета из первых принципов [10], а также в некоторых экспериментальных исследованиях [5, 7–9]. Проявление данного эффекта особенно важно учитывать при моделировании процесса диффузии водорода, так как он существенно повлияет на зависимость коэффициента диффузии от двухосных деформаций. Возможно также, что указанный эффект может служить причиной водородной кластеризации и влиять на фазовый переход ОЦК–ГЦК в железе с растворенным в нем водородом.

Работа поддержана грантом Российского научного фонда (проект № 16-19-10252).