Моментные функции стохастической краевой задачи структурной механики матричных композитов

In this work a stochastic boundary-value elasticity problem is formulated for structural-inhomogeneous media taking into account the moment functions which are capable of describing the real material structure. The appropriate analytical solution has been given to determine the field moments of structural stresses and strains of a composite consisting of randomly located spherical inclusions and a matrix. Numerical modeling has been performed to obtain the part of the structure in terms of the Monte-Carlo method, to statistically analyze this structure and to derive its moment functions of the second and third order. It has been found that these functions can be approximated analytically, which is necessary to calculate the moments of random fields of structural stresses and strains.

В настоящее время для построения механических моделей композитов широкое распространение получил структурно-феноменологический подход, основанный на том, что феноменологические уравнения и критерии механики деформируемого твердого тела рассматриваются на двух уровнях: структурном, в рамках которого описывается поведение элементов структуры, и макроскопическом, описывающем композиционный материал как однородный с эффективными свойствами.

В связи с этим удобно вместо всего объема композита ограничиться рассмотрением представительного объема I-го порядка малости V с характерным размером l таким, что l <<  L , где L - характерный размер конструкции [8].

В пределах элементарного объема 2-го порядка малости V k с характерным размером l k таким, что l k <<  l , композиционному материалу присваиваются свойства элементов структуры. На этом уровне представляется возможным исследовать процессы с помощью моделей и методов механики деформируемого твердого тела. При этом результаты исследований используются в континуальных уравнениях макроскопически однородной среды с помощью некоторых осредненных параметров.

Таким образом, в рамках структурно-феноменологической модели стохастическая краевая задача механики композитов в отсутствие массовых сил записывается в виде:

5a ij ⁽ r )

= o, 5 x j

⁸ ij

1 (a u, ( r ) a u ,( r r ) ( r ) = 2       i ' ^j

\

---+ у ОX j

dxi J

,

°ij (r) = Cijmn (r)8mn (r) , на границе Г заданы перемещения

U i (r)| Г = e „ r j ,                                            (2)

где G j ( r ) - структурные напряжения, £ ij ( r )- структурные деформации, C j _mn ( r )-тензор модулей упругости неоднородной среды, e_ij - компоненты произвольного заданного тензора малых макродеформаций.

Поля структурных напряжений G j ( r ) и деформаций £ j ( r ) являются случайными однородными всюду, за исключением области малой окрестности, прилегающей к границе Г . Для их описания используется статистический подход, связанный с нахождением моментов

M ji, =j(r)aЦ r) >,            V     £ j(r)sj( r) > .

Поле структурных модулей упругости C_ijmn ( r ^r ) является статистически однородным и описывается следующей зависимостью:

C ijmn ( Г ) = X ( Г)C ijmn + (1 -X (r» C im. •

Систему уравнений (1) преобразуем к виду d 2 Um' (r)

^jmn     a x . a X j

= —n ij , j ,

П , j = у x . ( ( < ^C ijmn ⁽ r ) > ⁺ C jmn ⁽ r ) ) e mn ⁺ C jmn ⁽ r ^)U m , n ) ^.

Полученное неоднородное дифференциальное уравнение будем решать методом функций Грина. При постоянном тензоре < Cijmn > функция Грина Gmk (rr ,rr1 ) или тензор Кельвина-Сомильяны вместе со своими производными обращается на бесконечности в нуль и удовлетворяет дифференциальным уравнениям ijmn

d ² G mk ( r , r 1 ) a x . a x j

-5 ik 5 ⁽ r - r ! ),

где 5 ( r -

r ^r ₁ )- дельта-функция или функция Дирака.

Если <  C jj _mn >  - изотропный тензор, то

G jmn ( r , Г 1 ) = A T^ I ^{r -} r l

+ B

⁽ r m ^- r l m ⁾⁽ r k ^- r l k )

где коэффициенты А и В связаны с постоянными Ламе тензора

< C ijmn >

соотношениями:

< X > + <  3 u >                          < X > + < H >

A =------------------- ,                  B =------------------- .

8 n< ( X + 2 p ) >                      8 n< ( X + 2 p ) >

r

Возвращаясь к решению краевой задачи, имеем для неизвестного поля Ui (r) интегро-дифференциальное уравнение dU' (r) ,dGy (r,r ') а и                          X                         X

—= J — X------ ^(( < C jnki ( r ') > + C jnki ( r ') ) e ki + C jnki ( r ') U k , i ( r ‘ ) ) dV' .

, dxa     v    dx a    dxn

Полученное уравнение будем решать методом последовательных приближений. Приведем решение в первом корреляционном приближении, поскольку в дальнейшем ограничимся рассмотрением только этого приближения:

д U i ‘ ( r ) ∂ x _α

д G j ( Г , Г ‘ ) д

∂xα    ∂xn′

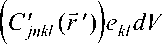
Для пульсаций структурных

напряжений и деформаций

справедливы

следующие соотношения:

∂

( r,r ')) — ( C inki ( r ‘ )e ki ) dV'

_∂ x_{n ′}      inkl kl

^а ( r ) = — ~J ( j ( r, r ‘ ) + G j

² V

° j '^{( r} ) ⁼ C i ^′ jmn ⁽ r ) e mn ^-<  ^C jmn ⁽ r Xn ⁽ r ) > ⁺ C ijmn ⁽ r )4 ⁽ r ) .

Видно, что пульсации напряжений и деформаций являются случайными однородными полями, определяемыми геометрией элементов структуры, их упругими свойствами и характером взаимного расположения. На основе этого переходим к решению задачи в моментах:

<^е у' ( r ) ^e_ae’ ( r ) >= 4 n e v» ( C f. - C m- >< C f - ^c m ) x                        (3)

X J J ( G .k , , ( r , r ") + G jk , i ( r, r "))( G a,, ( r , r "’ ) + G p, a ( r , r '" )) < X' ( r ") X' ( r ™) > , _e dV "dV ™ ,

VV

< a (r)° R (r) >= e e < C‘ (r)C‘   (r) >+ e < C >< C‘ (r)c (r ) > + ij αβ             kl γµ      ijkl αβγµ            kl αβγµ ijkl γµ

+ e < C >< C‘   (r)e‘ (r) > + < Ciik,x C ><£‘ (r)e' (r) > +

γµ ijkl αβγµ kl                ijkl αβγµ γµ kl

+ e < C' (r)C'   (r)£* (r) >+ e  < C'   (r)C' (r)e (r) > + kl ijkl αβγµ γµ            γµ αβγµ ijkl kl

⁺< C jki >< ^C a_Pro ⁽ r ) = ;_y ( r ^⁽ r ) >⁺< C a»Y. ><  Cy. r ) =; » ⁽ r ) = k, ( r ) >+

+ <  ^C i _1H ( r ) e k, ( r ) ><  C a_pTw ( ? ) = ;» ( r ) > + <  C a_№w ( r ) C jkl ( r ) = ;» ( ,^r )₆; ( r) > .         (4)

В качестве модели структурно-неоднородной среды рассматривается материал, который представляет собой однородную матрицу , где случайным, но равномерным образом расположены включения равного радиуса.

Для построения такой разреженной матричной структуры используется алгоритм, известный в литературе как метод Монте-Карло [4]. Суть его заключается в следующем.

В некоторую ограниченную область поочередно “выбрасываются” точки (центры сфер). Начиная со второй точки, производится вычисление расстояния между центрами сфер, которое не должно превышать значения 2d (d - радиус сферы). В случае, когда данное условие не выполняется, точка “уничтожается” и “выбрасывание” повторяется. Процесс продолжается до тех пор, пока не будет достигнута заданная объемная доля. При заданных объемной доле f ^ и числе включений N вычисляется радиус сферы d = a

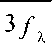
4 Nп

В противном случае, когда сделано предельное значение выбросов, но необходимое число точек не смогло разместиться в заданном объеме, вычисляется объемная доля, соответствующая вместившемуся количеству включений. Данный метод позволяет синтезировать разреженные структуры данного типа с объемным содержанием включений до 0,3.

Количественными характеристиками свойств синтезированной случайной структуры материала, необходимыми для решения статистических краевых задач механики структурно-неоднородных сред, являются моментные функции случайной индикаторной функции X ( r ) . Однако определение их вида для конкретных материалов требует ввода гипотез, нуждающихся в достаточном обосновании. Проблема может быть решена, если воспользоваться методами структурного моделирования на ЭВМ.

Вычислим моментную функцию второго порядка для синтезированной ранее случайной структуры:

K 2 ( r , Г Д =< X‘ ( r) X ‘ ( r ) >=< X ( r ) X ( r i ) > - < X ( r ) > ²,                  (5)

где X ( r ) есть индикаторная функция случайного поля, описывающая геометрию двухфазной структуры,

X( r ) =

1, r е сфе р е ;

0, r е матрице, здесь r - радиус-вектор, X'(r) - пульсация индикаторной функции, имеющая вид X '(r ) = X (r ) - (X (r)) , (...) - оператор статического осреднения.

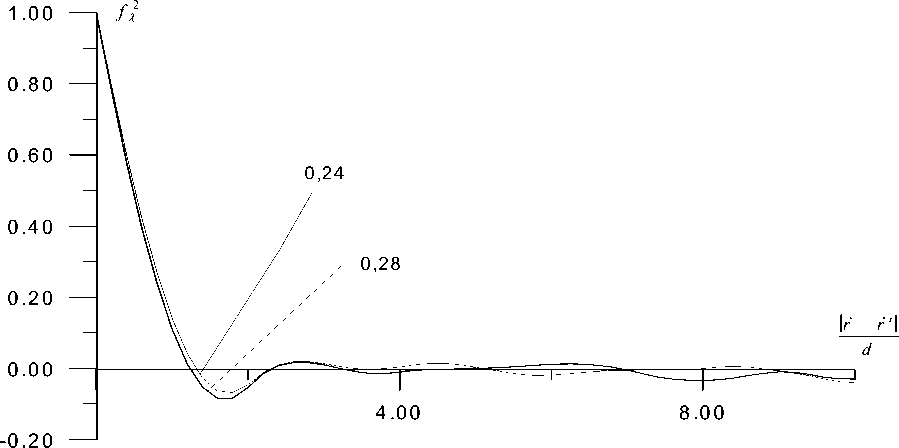
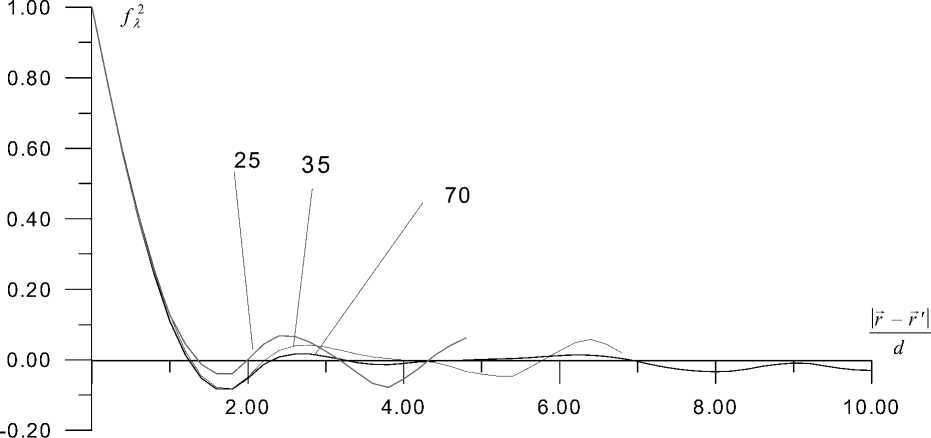
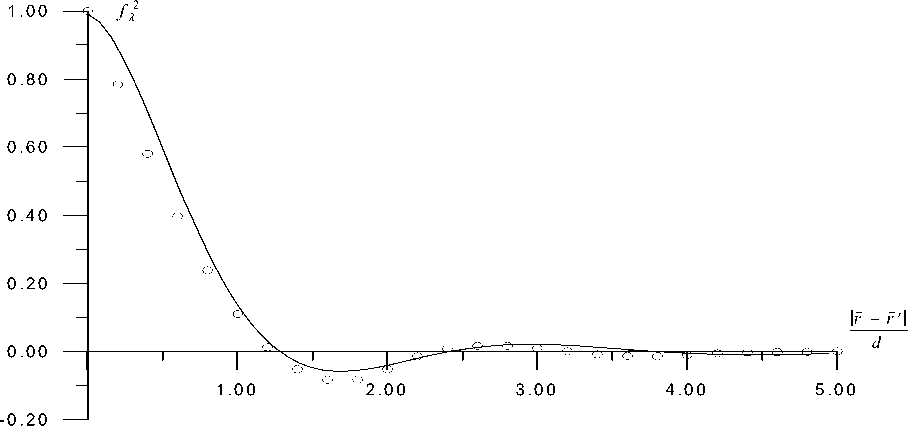
При построении корреляционной функции в синтезированном фрагменте случайной структуры выделяется куб, который разбивается сеткой с шагом h = у 2 d . В узлах сетки проверяется наличие включения или матрицы и параметру X(r) присваивается значение 1 или 0 соответственно. Для всех пар узловых точек, отстоящих друг от друга на расстоянии r - ri |, вычисляются произведения X(r)X(ri) и определяется их среднее значение суммированием всех произведений X(Г)X(ri) и делением их на количество рассматриваемых пар узловых точек. Для нулевого расстояния между точками находится значение

В силу того, что X( г ) - статистически однородная и изотропная функция, КX зависит только от расстояний между рассматриваемыми узлами r^r,r^r₁,r^r₂,r^r₃,... и инвариантна к их взаимному расположению, т. е. искомую моментную функцию n-го порядка можно представить в виде

К X( r • ri. r2....)= dX л (Ir - ri|. r - ri I. Iri - rit-),                 (6)

где f ⁿ_λ- нормированная корреляционная функция n-го порядка, Dⁿ_λ- центральный момент n-го порядка.

Рис. 1. Нормированная корреляционная функция 2-го порядка для случайных разреженных структур со сферическими включениями равного радиуса (r=0,39) с объемной долей р = 0,28; 0,24 при N = 70 (число разбиений ребра куба)

Рис. 2. Нормированная корреляционная функция 2-го порядка для случайных разреженных структур со сферическими включениями равного радиуса (r=0,39) с объемной долей р = 0,28 при N = 25, 35, 70

На представленных выше графиках корреляционная функция быстро убывает при увеличении аргумента. При переходе к меньшей объемной доле кривые становятся более пологими и сдвигаются в сторону увеличения аргумента (рис.1).Увеличение числа разбиений ребра куба N приводит к значительному затуханию нормированной корреляционной функции относительно оси абсцисс, что подтверждает достоверность полученных результатов (рис.2).

Статистический подход механики структурно-неоднородных сред предполагает вычисление безусловных моментов структурных напряжений и деформаций, что непосредственно связано с поиском явного вида нормированных моментных функций fx и fx случайного параметра X(r). Для этого построенная ранее на ЭВМ первая производная в нулевой точке [3]:

2| r r|          Jr - F1|\ fx r - ri | = exp(-cl —^2)

I r - r1                 r - r1

c 2 cos( c 3  ---2—) + c 4 sin(c52—)

d2

где d - радиус включений. Показано, что константы cl - c4 зависят от объемной доли включений и их численные значения соответственно равны (таблица):

Рис.3. Аппроксимированная нормированная корреляционная функция 2-го порядка для случайной разреженной структуры со сферическими включениями равного радиуса (r = 0,39) с объемной долей р = 0,28

константа	р=0,28	р=0,24
с1	1,03377243	1,04283448
с2	0,9904881	0,993981383
с3	1,8743548	1,859772621
с4	0,7296027	0,720358433

В соответствии с [2,3,7] может быть записано аналитическое выражение для моментной функции 3-го порядка случайного параметра Х(r) :

K 3(0, r, ri) = Dx³fx³(0, r, ri),

D X = р(1 - р)(1 - 2 р), где    f ^ (0, r , r1)- нормированная корреляционная функция 3-го порядка, D^ - центральный момент 3-го порядка параметра Х(r), r                    с1       2      2           2

fМr,ri) = exp^(-2^2⁽|r| + Ы + r^-ri| ))^x

X

c2 cos(

2d²

⁽l rl + lril²+ Ir

r2            c5

^-ri | )) + c^4sin(2d2

(|r |²+ |r,|²+ r-r,|²))

С помощью представленных формулами (6), (7), (8) функций определяются моментные функции 3-го и 4-го порядков, необходимые в дальнейшем для определения моментов 2-го порядка полей структурных деформаций и напряжений:

К 3(0,0, r ) = (1 - 2р) К 3(0, ri),

• ₄^rrrr ₃^rrr ₂rr К x(^u,°’^r, ri ) = ^{(1 2р)}К x(0,^r, ri)+^р(1 ^р)Лx(^r, ri) .

Таким образом, в данной работе была рассмотрена задача определения моментов полей структурных напряжений и деформаций для синтезированных случайных структур со сферическими включениями равного радиуса. Дальнейшее вычисление моментов (3), (4) производится с помощью численного интегрирования по области статистической зависимости.