Мониторинг динамических систем с трением и асимметрией колебаний

В теоретических исследованиях регулярной динамики нелинейной механической системы с сухим трением и динамическим воздействием вибрации используются законы классической механики, физики, теории колебаний, теории вибрационных процессов и устройств, а также основные представления о физических механизмах и видах асимметрии системы, познания о физической сущности массовых разделительных процессов в науке и технике (в технике обогащения полезных ископаемых, теплоэнергетике, химической технологии и др.). Анализ и синтез нелинейных механических колебательных систем включает общие вопросы механики и процессов управления: нелинейные задачи газо- и гидродинамики; волновые процессы и акустика; проблемы нелинейных колебаний в технике. Основным условием возникновения вибрационных эффектов, лежащих в основе ряда современных машин и технологий, является наличие асимметрии системы. Асимметрия системы может достигаться за счет асимметрии закона колебаний. Закономерности, лежащие в основе избирательного транспортирования мономинеральных полидисперсных материалов, продуктов различного вещественного состава в соответствии с их физико-механическими свойствами на поверхности подчиняются нелинейно вибрирующей механической системе при бигармоническом законе колебаний [1].

Рассмотрены закономерности динамических процессов при воздействии на систему волновых пилообразных по форме колебаний (saw-toothwaveinform). Мониторинг системы позволяет обеспечить выбор оптимальных динамических параметров вибрации для повышения транспортирующей способности разделительных процессов. Acимметричность продольных (возвратно-поступательных) колебательных движений механической системы (более быстрый ход назад) приводит к проявлению значительных инерционных сил, превышающих силы трения частиц полидисперсной смеси о поверхность, и к их продольному движению. Производительность системы как транспортного аппарата, как и энергия от продольных колебаний, зависит от амплитуды А и частоты ω периодических пилообразно-симметричных (асимметричных по направлению) колебаний. При этом абсолютное значение максимального ускорения ω = Аω ² при обратном ходе больше максимального ускорения при прямом ходе назад. За время продвижения материала происходит избирательное транспортирование частиц в соответствии с их коэффициентом трения, крупностью, а также формой. При этом на материал действуют: сила тяжести Р = mg ; сила динамического воздействия вибрации, определяемая абсолютной величиной максимального колебательного ускорения системы ω , сила трения, всегда направленная против движения материала. Сила трения F _тр возникает при наличии контакта материала с поверхностью вибрирующей системы, наличие угла наклона α которой способствует эффективности разделительного процесса. Для теоретического представления приведенные силы учитывают все факторы динамического процесса. Балансовое соотношение силы трения может быть представлено в следующем виде:

В.Д. Анахин . Мониторинг динамических систем с трением и асимметрией колебаний

F tp = xfmg cos a , (1) где x = ± 1; f - эффективный коэффициент трения. При ш₁ = - Ш 2/В > 0, где w ₁ и w ₂ - соответственно, колебательные ускорения системы в положительном и отрицательном направлениях. Материал движется с положительным ускорением:

a ₁ = x- f - cos a - g - sin a

Скорость продольного перемещения материала зависит от абсолютного значения максимального ускорения вибрирующей поверхности и от соотношения периодов прямого Т ₁ , обратного Т ₂ ходов и общего Т периодов колебаний системы:

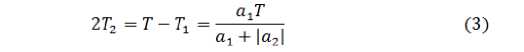
В период обратного скольжения Т2 материал движется с отрицательным ускорением:

a ₂ = I a ₂1 = - f- g - cos a - g - sin a

Для удобства расчетов введем следующие условные обозначения:

A = f- g - cos a

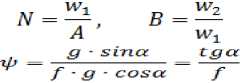
Примем также кинематические обозначения: v 1 ,v 2 , – скорости скольжения частиц, u 1 , u 2 , – колебательные скорости системы, t 1 , t 2 – время этапов, соответственно, прямого и обратного колебательного вибросмещения системы. В зависимости от соотношения колебательных ускорений системы и скольжения материала возможны следующие технологические режимы и наблюдаются следующие общие закономерности поведения системы (не загромождая излагаемый материал математическими выкладками, ограничимся записью формул скорости в конечном виде):

• 1.    I - T >  N, I + T >  BN (a1 = w ₁ и a ₂ = w ₂ ) - преобладание сил трения;

• 2.    I - T >  N, I + T <  BN , a ₁ = w ₁ - проскальзывание

• 3.   a ₂ = A - T A, v₁ = и 1, t ₁ = 0, t ₂ = T ₂ , I a ₂1 < I w ₂1 - скольжение

v2 = 1 Oi + v2) = 1 («! + Ui — |a2 | - T2) = i z i +       ix

• 2    ”BAT 11 + 0 + BW ~ В I 1 ) ~ средняя скорость частиц;

  4. I - T <  N, I + T >  BN, a2 = w2, ai = T A + A V 2 = U 2, t2= 2t1, T2 = 2 т - t1 ,

  
  
  

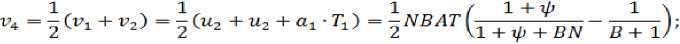
• 5. I - T <  N, I + T <  BNa1 = A - T A ,

T, = T —-,r₂ - T—

1         2     2         2

v4 = — (vx + v2) = ^^^ В + 1 ^ — Bty2 + V^2 — 2.BNxp — 1).

Полученные зависимости свидетельствуют, что во всех режимах, за исключением 1, средняя скорость частиц линейно растет с ростом периода колебаний и возрастает до определенного предела при увеличении асимметричности колебаний системы, определяемой значением параметра В. Для режима 2 абсолютное значение максимального колебательного ускорения системы имеет оптимальную величину при N = N*, I - T = N* .

Расчет скоростей движения частиц в этом режиме производится по формуле:

Чг* = | (1 + Ч^АТ Q^^ ~" ^7)(5)

Для режима 3 оптимальное значение колебательного ускорения системы достигается при BN = (BN)*, I + Ψ = (BN) . Скорость движения частиц определяется по следующей формуле:

• 1           /1 —1 X

^'-^d + V-MTf—)(6)

Если. то      0 Производительность процесса недостаточна.

Угол наклона механической системы α и динамический вибрационный параметр В = ω₂ / ω₁ являются основными регулируемыми параметрами при эксплуатации системы. При В → ∞ скорость скольжения достигает максимального значения при существенном возрастании динамической нагрузки. Оптимальная величина соответствует значению В = 9 и связана с соотношением N = ω1 / fg∙cos ω . Дальнейшее увеличение скорости нежелательно.

Продольный угол наклона α способствует лучшему разделительному процессу. При горизонтальном положении поверхности системы наиболее высокие скорости скольжения достигают в режиме 4. При продольном подъеме поверхности средняя скорость движения материала по вибрирующей поверхности механической системы достигает наибольших величин при α= 2-3 град и более в режиме 2. Наличие этого подъема способствует увеличению сил трения и способствует лучшему разделительному процессу по коэффициентам трения f , а также крупности и форме минералов, характеризуемой коэффициентом формы (0,6-1,0). Коэффициент трения скольжения определим по формуле f= tgα (B+1)/(B-1).

Дифференциальный привод с асимметричными колебаниями увеличивает скорости передвижения частиц материала линейно с ростом численного значения коэффициента трения f , обеспечивая эффективность транспортирования и более экономичную технологическую схему.