Моногармонический метод расчета частотных характеристик динамической жесткости нелинейных динамических объектов

Демпфирующие свойства упругих систем принято оценивать с помощью характеристик динамической жесткости [1, 2], под которой понимается передаточная функция G ( s ), определяемая отношением изображения по Лапласу силы (момента силы), действующей на выходное звено системы, к изображению линейного (углового) перемещения выходного звена системы, вызванного этой силой (моментом силы):

или

G (s )

R (s )

X(s )

G ( s )

M ( s ) a( s ) ’

где R ( s ) — изображение по Лапласу силы, действующей на выходное звено системы; X ( s ) — изображение по Лапласу линейного перемещения выходного звена системы под действием силы; М ( s ) — изображение по Лапласу момента силы, действующего на выходное звено системы; α( s ) — изображение по Лапласу углового перемещения выходного звена системы под действием момента силы.

В большинстве работ, посвященных исследованиям динамической жесткости гидравлических приводов и бустеров летательных аппаратов, частотные характеристики определяются после проведения линеаризации математических моделей исследуемых динамических объектов, поэтому приводимые в них характеристики динамической жесткости носят гладкий характер, как, например, в работе [3].

Однако известно, что достоверные частотные характеристики для нелинейных систем могут быть получены только посредством возбуждения их гармоническими входными сигналами на различных фиксированных частотах, с последующим анализом реакций на эти возбуждения методом Фурье [4].

В работе [5] авторами установлено, что переходные процессы втягивания в вынужденные колебания при входном моногармоническом воздействии даже у некоторых линейных динамических объектов могут длиться достаточно долго. Поэтому для нелинейных и некоторых линейных динамических объектов заранее никогда не известно число периодов входного моногармонического сигнала, в течение которого длится переходный процесс втягивания в вынужденные колебания. Игнорирование этой особенности при расчетах частотных характеристик может приводить к существенным ошибкам.

Чтобы устранить влияние переходных процессов втягивания системы в вынужденные колебания, известным алгоритмом расчета [6] характеристик динамической жесткости бустера предписывается проводить интегрирование в течение шести периодов колебаний входного моногармонического сигнала на каждой из фиксированных частот. При этом амплитуды и фазовые запаздывания первых гармоник выходных сигналов рассчитываются по последним (шестым) периодам. Однако этот алгоритм не гарантирует получения точных результатов, так как в нем отсутствуют операции завершенности переходного процесса втягивания в вынужденные колебания. Кроме этого, автор работы не приводит результаты расчетов частотных характеристик бустера, получаемые этим методом, а ограничивается только описанием алгоритма и математической модели бустера.

В связи с этим определенный теоретический и практический интерес представляет задача разработки методов и алгоритмов расчета частотных характеристик динамической жесткости динамических объектов и следящих систем, позволяющих получать результаты с заданной погрешностью вычислений и за минимальное время (так называемых методов «автоинтегрирования») [7].

До определенного времени создание и внедрение подобных методов и алгоритмов для расчета частотных характеристик следящих систем и других сложных динамических объектов, основанных на численном интегрировании нелинейных дифференциальных уравнений их математических моделей при моногармонических входных воздействиях, сдерживались низким уровнем быстродействия вычислительной техники.

Стремительное развитие вычислительной техники и совершенствование ее характеристик (в частности, возрастание уровня быстродействия компьютеров) в последние годы позволили практически полностью переориентировать методы расчета частотных характеристик динамических объектов и систем на более точные, основанные на численном интегрировании дифференциальных уравнений математических моделей систем при моногармонических входных воздействиях на фиксированных частотах и анализе откликов на эти воздействия методом Фурье.

Анализ постоянства параметров откликов динамических объектов и систем на моногармонические входные воздействия можно проводить различными способами, которые, в частности, могут быть основаны на сравнении вычисляемых значений амплитуд и фазовых сдвигов или на сравнении вычисляемых значений коэффициентов Фурье исследуемых гармоник выходных сигналов (откликов).

В работе [4] показано, что наиболее эффективные алгоритмы метода автоинтегрирования должны базироваться на сравнении действительных и мнимых составляющих (коэффициентов Фурье) исследуемой гармоники периодического отклика динамического объекта на входное моногармоническое воздействие. При таком подходе к построению методов и алгоритмов существенно сокращается продолжительность вычислений частотных характеристик нелинейных динамических объектов.

Сравнение результатов расчетов частотных характеристик, приведенных в работах [8, 9], показало, что наиболее эффективным алгоритмом моногармо-нического метода автоинтегрирования является вариант метода с полным осреднением коэффициентов Фурье, согласно которому анализ постоянства коэффициентов Фурье исследуемой гармоники выходного сигнала динамического объекта или системы управления осуществляется путем сравнения средних за n–k периодов значений коэффициентов Фурье исследуемой гармоники выходного периодического сигнала динамического объекта или системы управления, получаемыми на n -ном периоде входного моногармонического сигнала (здесь k — число неанализируемых периодов), со средними значениями этих же параметров на ( n – 1)-ом периоде.

Этот метод существенно сокращает продолжительность вычислений и позволяет более точно рассчитывать частотные характеристики любых гармоник нелинейных динамических объектов и систем управления.

Алгоритм моногармонического метода расчета частотных характеристик динамической жесткости

Алгоритм моногармонического метода расчета частотных характеристик динамической жесткости имеет два основных цикла — по частоте и по времени. В цикле по частоте производится присвоение переменной частоты значения частоты из массива частот в соответствии со счетчиком номера частоты, при этом номер частоты nf изменяется от nf = 1 до nf = nfm. На каждой из фиксированных частот f(nf) входной моногармонический силовой (моментный) сигнал вычисляется по следующим соотношениям:

• а)    для линейного перемещения выходного звена

R = А_R sin[2π f ( nf ) t ];

• б)    для углового перемещения выходного звена

M = А_M sin[2π f ( nf ) t ];

где R — текущее значение внешнего усилия, прилагаемого к камере; А_R — амплитуда внешнего усилия; М — текущее значение внешнего момента, прилагаемого к камере; А_M — амплитуда внешнего момента; t — время.

Чтобы получать результаты расчетов с одинаковой точностью на каждой из фиксированных частот входного моно-гармонического сигнала, шаг интегрирования h по времени варьируется, и его значение в зависимости от частоты f вычисляется по выражению

1 h=Iff7 ’ где Kf — коэффициент, определяющий максимальное значение шага интегрирования на минимальной частоте входного моногармонического сигнала, при котором процесс интегрирования имеет устойчивый характер (определяется экспериментально для каждой конкретной математической модели).

На каждой частоте в цикле по времени выполняется интегрирование дифференциальных уравнений исследуемого динамического объекта или системы управления, при этом в течение первых k периодов входного моногар-монического сигнала, где искажения наиболее велики, а номер периода i ≤ k , операции анализа не проводятся. По завершении k -го периода на каждом из следующих периодов последовательно выполняются следующие действия:

• • вычисляются коэффициенты Фурье исследуемой гармоники динамической жесткости по соотношениям:

P ( i , l ) ≈ 2 fhE_m ( i , l );

Q ( i, l ) ≈ 2 fhF_m ( i, l ), где

• а)    для линейного перемещения выходного звена

Em(i, l) = 1L {[R(t)/Y(t )]cos(2nlft) + m               2 j = i           ,j            ’ j,

+ [ R ( t_{i , j – 1} )/ Y ( t_{i , j –1} )]cos(2π lft_{i , j –1} )};

Fm(i, l) = 1 L {[R(t)/Y(t)]sin(2nlft) + m                2 j = i           i, j            i, ji, j

+ [ R ( t_{i , j –1} )/ Y ( t_{i , j –1} )]sin(2π lft_{i , j –1} )};

• б)    для углового перемещения выходного звена

Em(i, l) = 11m {[M(t)/a(ty)]cos(2nlft) + m                2 j = i            , j            * j*

+ [ M ( t_{i , j –1} )/α( t_{i , j –1} )]cos(2π lft_{i , j –1} )};

Fm(i, l) = 1 Ll {[m(t )/a(t )]sin(2nlft ) + m                 2 j = i            , j            , j,

+ [M(ti, j–1)/α(ti, j–1)]sin(2πlfti, j–1)}, где l — номер гармоники; P(i, l), Q(i, l) — вычисленные на i-м периоде входного моногармонического воздействия коэффициенты Фурье l-й гармоники выходного сигнала Y(t) или α(t); h — шаг интегрирования; j — номер шага; m = T/h — число шагов h, содержащихся в одном периоде входного моногар–мони-ческого сигнала; ti j = iT + jh, j = 0, m — сетка моментов времени численного интегрирования методом трапеций;

• •    определяются средние значения коэффициентов Фурье исследуемой гармоники динамической жесткости за пройденное количество анализируемых периодов входного моногармонического сигнала

n

L P( i L)

г = k+1 ___________ N — К ’

P_c ( n, l )

Q_c ( n, l )

£ Qf, h i = k +1_________ n k где n — значение номера последнего периода входного моногармонического сигнала;

• •    проводится анализ достаточности постоянства средних значений коэффициентов Фурье анализируемой гармоники по выражениям

I I P c ( n , l )I - I P c ( n - 1, l )I

|             P c ( n , I )

I Q c ( n , l ) I - I Q c ( n - 1, l ) I

Q c ( n , l )

I -100 C e; I -100 C e,

управления вектором тяги ракетного блока представлена на рис. 1.

где ε — число, регламентирующее заданную погрешность вычислений в процентах;

• •    если оба неравенства выполняются, тогда вычисляются:

• а)    амплитуда динамической жесткости B_l исследуемой l -й гармоники выходного сигнала по средним значениям коэффициентов Фурье на последнем периоде входного моногармонического сигнала

B_t = V P ²( n , l ) + Q 2 ( n , l );            (1)

• б)    фазовый сдвиг исследуемой гармоники динамической жесткости к входному моногармоническому сигналу по средним значениям коэффициентов Фурье исследуемой гармоники на последнем периоде входного моногармони-ческого сигнала

  лок описаний

  

  Установка счетчика

  номера частоты

  числа периодов

  Установка счетчика

  числа шагов

  интегрирования

  условий

  Установка счетчика

  Блок интегрирования диффсрснииа.льных уравнений системы

  
  

V(n, l) при Qc(n, l)>0 и Pc(n, l)<0; (2)

Блок вычисления коэффициентов Фурье исследуемой гармоники динамической жесткости

-n + y(n, l) при Qc(n, l)<0 и Pc(n, l) < 0;

Фl = < -n+y(n, l) при Qc(n, l)<0 и Pc(n, l)>0;

-2n+v(n, l) при Qc(n, l)>0 и Pc(n, l)>0;

n[-1 - 0,5signPc(n, l)] при Qc(n, l) = 0,

Блок вычисления средних значений коэффициентов Фурье исследуемой гармоники динамической жесткости

„          p ( n, l )

где v( n, L) = arctg ^c .

Q c ^{( N, L} )

Для получения логарифмических амплитудных частотных характеристик (ЛАЧХ) динамической жесткости вместо соотношения (1) используется выражение

A lL = 20 lg( B l ).

С целью построения фазовых частотных характеристик (ФЧХ) динамической жесткости для получения фазового сдвига в градусах используется выражение вместо (2)

Φ _l = 57,295 ϕ _l .

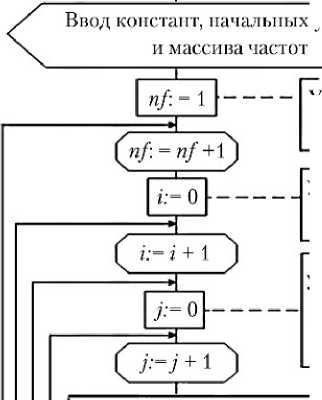
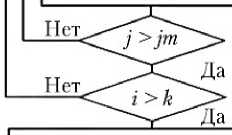
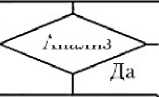
Блок-схема алгоритма моногармо-нического метода автоинтегрирования для расчета частотных характеристик динамической жесткости системы

Пет

Анализ

- l^p>Qi 1Л(" 1-01 /',(”. 0

Блок вычисления амплитуды и фазового сдвига

-100 < с

lQ,(n,0 - ф»-1,/)1

<2,<»0

Занесение результатов расчетов в массивы

—<7п/ >  njmj>

Печать результатов расчетов и рисование графиков _

Рис. 1. Блок-схема алгоритма моногармонического метода автоинтегрирования для расчета частотных характеристик динамической жесткости

Тестовый нелинейный динамический объект и его математическая модель

В качестве тестового нелинейного динамического объекта был выбран силовой гидроцилиндр (гидродвигатель с линейным перемещением выходного органа) с перекрытыми гидромагистралями. Этот объект для тестирования был выбран потому, что содержит существенную нелинейность в виде классического сухого кулоновского трения, представляющую собой разрыв первого рода. Математические модели объектов, содержащие такую нелинейность, поддаются расчетам частотных характеристик с очень большими затратами машинного времени.

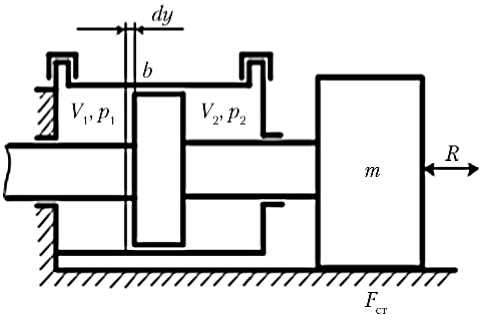
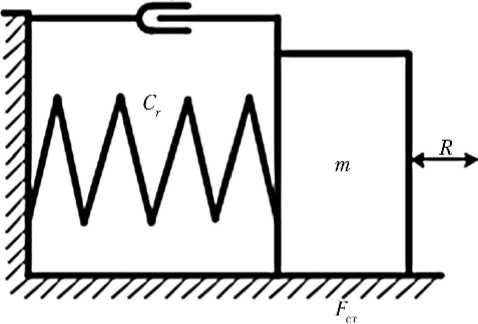
Принципиальная гидромеханическая схема и динамическая модель выбранного нелинейного динамического объекта представлены на рис. 2, где C _г — коэффициент упругости «гидравлической пружины».

Математическая модель тестового нелинейного динамического объекта представляет собой систему следующих нелинейных дифференциальных уравнений, описывающих режимы покоя и движения при моногармонической вынуждающей силе:

dY _dt = V,

dV Σ F

dt m где m — суммарная масса поршня, штока и нагрузки; Y — перемещение нагрузки; V — скорость перемещения нагрузки; ∑F — сумма сил, действующих на нагрузку, для режимов покоя и движения, определяемая как

R - S J p 1 - p 2 ) - F _cm sign V - bV при V * 0,

а)

S F = <

R – S _п ( p ₁ – p ₂ ) – F _ст sign[ R – S _п ( p ₁ – p ₂ )]

при V = 0 и I R - S _n ( p i - p 2 ) | >  F ст ,

0 при V = 0 и | R - S _n ( p 1 - p ₂ )|< F ст ,

b

б)

Рис. 2. Принципиальная гидромеханическая схема и динамическая модель силового гидроцилиндра с перекрытыми гидромагистралями: а — принципиальная гидромеханическая схема; б — динамическая модель

где b — коэффициент вязкого трения в гидроцилиндре; F _ст — сила сухого трения в гидроцилиндре; S _п — эффективная площадь поршня; p ₁ и p ₂ — давления в полостях гидроцилиндра, определяемые дифференциальными уравнениями

1Eж ^п’     V dt = Vo+snd; - y) ’ dp2          EжSп     V dt = – V 0 + Sп(Y0 + Y) , где Eж — объемный модуль упругости жидкости; Y0 — координата начального положения поршня гидроцилиндра; V0 — остаточный объем жидкости при постановке поршня на упор.

На параметры математической модели объекта накладываются следующие ограничения:

• •    если p ₁ < 0, то p ₁ = 0;

• •    если p ₂ < 0, то p ₂ = 0;

• •    если Y >  Y ₀ , то Y = Y ₀ , V = 0;

• •    если Y < – Y ₀ , то Y = – Y ₀ , V = 0.

Начальные условия:

при t = 0 → Y = Y _min ; V = 0; p ₁ = 0; p ₂ = 0, где Y _min — начальное значение перемещения поршня гидроцилиндра, принимаемое в начальный момент времени отличным от нуля во избежание в процессе счета возникновения операции деления на ноль (определяется экспериментально для каждой конкретной математической модели).

Поставленная тестовая задача — расчет частотных характеристик первой гармоники динамической жесткости силового гидроцилиндра с перекрытыми магистралями.

Результаты вычислительного эксперимента

ЛАЧХ и ФЧХ первой гармоники динамической жесткости нелинейной математической модели силового гидроцилиндра с перекрытыми гидромагистралями рассчитывались для следующего ряда фиксированных частот f ( nf ) (Гц): 1,0; 1,3; 2,0; 2,3; … 8,0; 8,3; 9,0; 9,3; 10,0; 13,0; 20,0; 23,0; … 80,0; 83,0; 90,0; 93,0; 100,0. Амплитуда входного воздействия системы в процессе вычислений составляла А_R = 1 000 Н и А_R = 2 000 Н, погрешность вычислений была принята равной ε = 0,01%, а K_f = 40 000.

Для расчетов были приняты следующие значения параметров в принятой для гидравлических расчетов системе (кгс, с, см), при этом в скобках указаны значения этих параметров в системе СИ:

F _ст = 25 кгс (245,25 Н);

E _ж = 1,24⋅10⁴ кгс/см² (1,21⋅10⁹ Па);

m = 0,5 кгс⋅с²/см (490 кг);

b = 10³ Н⋅с/м;

• Y ₀ = 1,7 см (1,7⋅10^–2 м);

• V ₀ = 1 см³ (1⋅10^–6 м³);

S _п = 9,62 см² (9,62⋅10^–6 м²);

Y _min = 1⋅10^–8 см (1⋅10^–10 м).

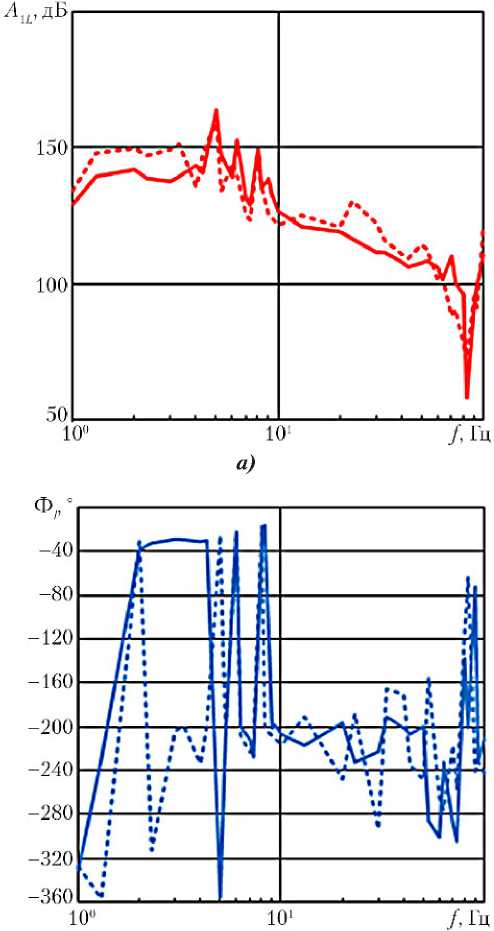
Результаты вычислительных экспериментов по расчетам частотных характеристик первой гармоники динамической жесткости силового гидроцилиндра с перекрытыми гидромагистралями с использованием представленной математической модели представлены на рис. 3 и 4.

Как видно из рассмотрения рисунков, графики ЛАЧХ и ФЧХ динамической жесткости силового гидроцилиндра с перекрытыми гидромагистралями для обеих амплитуд входного моно-гармонического силового воздействия имеют корреляцию во всем диапазоне частот, что свидетельствует о правильности разработанного метода.

Дальнейшие вычислительные эксперименты показали возможность вычисления ЛАЧХ и ФЧХ любых гармоник динамической жесткости тестируемого динамического объекта с помощью предложенного метода.

б)

Рис. 3. Логарифмические амплитудные частотные характеристики (а) и фазовые частотные характеристики (б) первой гармоники динамической жесткости силового гидроцилиндра с перекрытыми магистралями: ■ , ■ — A = 1 000 Н; , — A = 2 000 Н

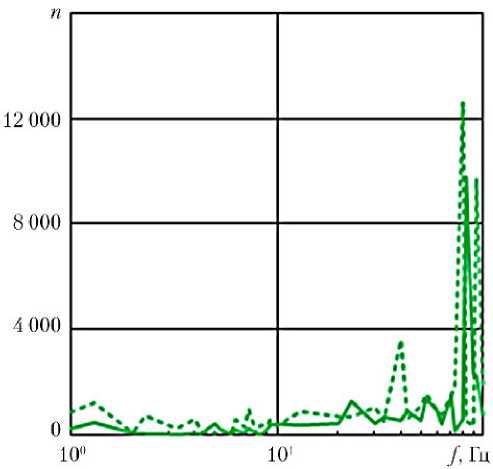
Рис. 4. Зависимость n(f) для достижения заданной погрешности вычислений логарифмических амплитудных частотных характеристик и фазовых частотных характеристик первой гармоники динамической жесткости гиДроцилинДра: ■ — A = 1 000 Н; — A = 2 000 Н

Заключение

Разработан моногармонический метод автоинтегрирования для расчета частотных характеристик динамической жесткости нелинейных динамических объектов с заданной погрешностью вычислений и за минимальное время.

Исследована работоспособность разработанного метода расчета путем проведения вычислительных экспериментов.

Результаты расчетов частотных характеристик динамической жесткости могут быть использованы для оценки демпфирующих свойств нелинейных динамических объектов.