Монотонность функции биномиального распределения возле медианы

Для биномиальной случайной величины £ с параметрами n е N и Ь/n хорошо известно, что ее медиана равна Ь, если Ь е {1,..., n} [1]. Рассмотрим биномиальную случайную величину ^ь,п,_с с параметрами n и дущ, г де Ь < n — натуральные числа и с е (0,1). Обозначим Рь,п,с := Р(£ь,п,с < Ь). В статье [2] доказана

Теорема 1. Справедливи следующие утвероюдения:

• •    Если n > 3Ь + 2, то р_ь+і,„,о >  Ръ,п,о-

• •    Если n 6 3Ь + 1, то р_ь+і,„,о <  Ръ,п,о-

  Заметим, что в 1968 году Джогдео и Самуэльс [3] изучали поведения вероятности рь,п,о, а также отношения Р(£ = Ь) и 1/2 — Р(£ < Ь), что мотивировано известным вопросом Рамануджана, относящимся к пуассоновским случайным величинам (см., например, [4]).

Кроме того, исследование монотонности рь,_п,_с^п0 b мотивировано задачей о неравенстве малых отклонений (см., например, [5]), которая может быть сформулирована следующим образом: для с > 0 найти минимум Р(Д + Д + • •• + би < п + с) по всем множествам независимых неотрицательных случайных величин {^1, • ••,^_п} с одинаковым средним. Эта задача до сих пор не решена. Тем не менее, было показано (см., например, [6]), что оптимальными случайными величинами являются величины, принимающие два значения с вероятностью 1 (как говорится, с двумя атомами). Если мы далее ограничимся одинаково распределенными случайными величинами с двумя атомами, то сведем исходную задачу к анализу монотонности рь,_п,с ^п0 b.

В настоящей работе доказано, что если с = 1, то справедлив а монотонность рқ_п,_с по b.

Теорема 2. Если с = 1, то рь+1,_п,_с > рь,_п,_с тіргі любых 1 6 b < п.

Из монотонности рь _п 1 следует приведенная далее гипотеза, ранее сформулированная в [2].

Гипотеза 1. Пусти а Е (0,1), Р > 1. Пустъ b — целое число такое, что п + 1 — па b < —------ 6 b + 1

р — а

Тогда РД1 + ••• + б_п<п + 1) >  рь,_пд> г де р, •••, бп — независимые одинаково распределенные случайные величины со средним 1, и равенство выполняется тогда и только тогда, когда а = 0 и ^+1 = b + 1.

Аналогичные этой гипотезе утверждения можно сформулировать для любого с Е (0,1). В этой связи в данной статье исследована монотонность для всех с Е (0,1).

Во-первых, обобщен первый пункт теоремы 1 на случай произвольного с Е [0,1].

Теорема 3. Если п > 3b + 2, то рь+1,_п, _с > рь,_п , с-

Во-вторых, получен асимптотический результат, утверждающий, что порог, при котором монотонность меняется, равен зд—) (1 + °(1))-

Теорема 4. Ve > 0 V d >  0 V с Е (0,1) Зпд V п > по V b Е (еп, п) :

,     п(1-5)

• •    при b <  ₃(_{1 - с}) выполнено ръ+1,п > рь,п

п(1+<5)

• •    при b >  ₃(1__с) выполнено рь+1,п < рь,п

• 2.    Вспомогательные утверждения

Благодаря этому существенно обобщена теорема 1 и получен инструмент, с помощью которого можно сформулировать следствия, аналогичные гипотезе 1.

Далее в статье будут использованы следующие обозначения:

• 1)    ^^ь,п+с = [1^— (Эс , ^{1 —} п+с ];

• 2)    g(z) = (1 — ю^ь '.;" ^ь:

• 3)    дь,п,с = f_bb+_+c g⁽z)dz.

• 2.1.    Полезное выражение для pb,n,c

В этом разделе обобщим на случай произвольного с утверждения 1-3 из статьи [2].

Утверждение 1.

b            n—b pb+1,n,c   РЬ,п,с —

(n+c) (1 - П+с)    - 61 — Я (1 - )b   •' bаг b /0(1 - г)ь—1гп—bdz

Доказательство. Запишем pb,_n следующим способом:

^p b,n,c

'  ⁽ .

(n - b + 1)!(b - 1 - .)!

(n -.)!

(У( *

-

b

n + с

)

n—i

Поскольку

(n - b)!(b - 1 - .)!

(n -.)!

Г(п - b + 1)r(b - .) Г(п - . + 1)

— B(n - b + 1,b - .) — [

x^n—b(1 - x)^{b— i—} 1 dx,

получаем pb,n,c — п(П _ 1)x x   К (b - 1) (1 - Ж)Ь—i—1 (—У (1 - —) b—i—1   b (1 - —) n—b+1 ' —

J 0 [i=0k .  /            V^{+ с}) V   ^{n + c}) J V ^{n + с}/

• —...;: „П +-_-> (- :.)Г....... (- +).....-—

—+-я -л. I' л лдгіт +)Г-м +>

₌     ^r(n+1)     г^1—^ь _ b—1 „—ь, ₌ JoJ ; ⁺ : (1_z_^г^n-bd^г

r(n - b + 1)r(b)./0      ⁽     )                  O¹ ! - z)b— 1zn—bdz ■

Следовательно, pb+1,n,c   pb,n,c —

J ₀1 ^n+c (1 - z)^bz^n—b—1 dz J 01(1 - z)^bz^n—b—1dz

1 — я

J₀^n+c (1 - z)^b—1z^n—b dz J 01(1 - z)^b—1z^n—bdz

1__ b+1                                          -|__ b

J₀  ^n+c (1 - z)^bd ( z^n—b )     f₀   " ^{+ c} (1 - z) ^{b— 1} z ^n—b dz

J01(1 - z)^bd (z^n—b)         J₀¹(1 - z)^b—1z^n—b dz

(n+c)  (1 - n+c)    + b Jo  n+c (1 - z)b 1zn bdz   Л1 n+c (1 - z)b—1zn—bdz b.f^a - z)b—1zn—bdz                      J01(1 - z)b—1zn—bdz b            n—b       — b

(Й1) (1 - n+c)    - aj,(1 - г)b 1г"bdг n + c|—I b 1'1(1 - z)b- 1zn—bdz

• 2.2.    Изучение поведения д

В статье [2] приведено следующее

Утверждение 2. Пусть I € {1,..., min{6 — 1, п — 6}}. Тогда

^һ- — Л _ -\M-Ln-b-l ^ +), іЛ-М-» ^{(п — 1 —} Ж ^{(п — 6)!}

дг^{1 (1 г)}      ^      »= г ⁽ 1) ^ (п — 1 — I)! (п — 6 - г)!^.

Аналогично статье [2], используя утверждение 2 и формулу Тейлора с остаточным членом в форме Лагранжа, получим верхнюю и нижнюю оценку для д(г) на Аь,и+С.

Обозначим для любого I € Z+, дкг)=1 (г—1+6+1) [ % (1—6+1)] L | С          г              п | С l-м членом разложения д по формуле Тейлора, и д^з(г) = ^3=qд-(г). Также обозначим

-- «- § (1 — 6+1), Щг) = § (1 — А-). г          п | С                      2          п | С

Из доказательства утверждения 3 получаем, что для любого 5 6 6 6 п/2, функции d₄ и d₄ являются нижними и верхними оценками д ⁴д/дг⁴ на Ақ_и + _С.

Утверждение 3. Для 5 6 6 6 п/3 и всех г € Аь,_и+_С,

5бз(г) + д+(г) > д(г) > д«з(г) + д—(г), где

д— ^(г) =

214 ( ^{г — 1 +} + ) ^d-(+

ДСН^ ( ^{2 —1 +} бД ) -№■

Доказательство. Для каждого I € {1,..., min{6 — 1, п — 6}}, обозначим _     д¹д/дг¹

^{/ l} (1 г)Ь-1— 1г ^п —b—i .

Легко видеть, что для каждого I, д/-+1/дг = —(I + 1)(п — I — 1)/-, и /2(г) = г2 (п — 1)(п — 2) — 2г(п — 2)(п — 6) + (п — 6)(п — 6 — 1)

отрицательна на

( п — 6

п — 1

—

п —

/Е—6ЖН5

V п — 2

п —

п — 1

+

п — 1

I (п —6)(6— 1)

N п — 2 J .

Давайте покажем, что Аь,_п + _С С Т. Во-первых,

1 — 6+1 > 1 — 6+1 >п—6 п + с       п п — 1

—

п —

/ (п —6)(6— 1)

V п — 2

так как разница между центральной

( ^— - b)(b—1) V и—2

2п—b—1 и

И

и правой сторонами этого неравенства равна

п2(п — 6)(6 — 1) — (2п — 6 — 1)2(п — 2) =

= п(Ь — 5)(п(п — Ь) — Ь) + п(12п — 156 — 9) + 2Ь2 + 2 + 4Ь > 0, поскольку 5 6 Ь 6 п/3. Во-вторых,

1—

Ь п + с

<

п — Ь

п — 1

+

п — 1

/ (п — Ь)(Ь — 1)

V п — 2

эквивалентно неравенству

(п —

1)(п + с —

Ь) — (п — Ь)(п + с) < (п + с) J ^{( п   Ь )( Ь}   1)

V п — 2

В данном неравенстве левая часть равна (1 + с)Ь — (п + с), что при п > Ь не превосходит с(Ь — 1). Поскольку п + с < Ь — 1, правая часть больше, чем (Ь — 1) ^(п П — П +)’ причем выражение под корнем больше 1. Получаем, что / 3 (z) возрастает на Аь,_п+_С.

Теперь покажем, что /3 (1 — ^) < 0. Замет им, что /3 (1 — ^) = — Р (Ь,п,с)/(с + п)³, где Р (Ь, п, с) = (5Ь — 6)п³ + (18Ь — 18с+ 21Ьс — 3Ь²с — 12Ь2)п² + (3Ь³с+ 7Ь³ — 9Ь ² с 2 — 39Ь 2 с — 18Ь² + + 27Ьс² + 36Ьс — 18с²)п + Ь ³ с ³ + 9Ь³с² + 18Ь³с + 6Ь³ — 6Ь²с³ — 27Ь2с² — 18Ь2с + 11Ьс³ + 18Ьс² — 6с³.

Покажем, что Р (Ь, п, с) положителен. Поскольку 5 6 Ь 6 п/3, рассматривая первые два слагаемых, получаем, что (5Ь — 6)п³ + (18Ь — 18с+21Ьс — 3Ь²с — 12Ь2)п² > (5Ь—6)п²• 3Ь+ (18Ь— — 18с + 21Ьс — 3Ь²с — 12Ь2)п² = С(Ь, с)п². где С(Ь, с) = 3(1 — с)Ь² + 21сЬ — 18с. Величина С(Ь, с) как многочлен от Ь имеет точку минимума Ь = —7с/(2(1 — с)), следовательно, возрастает при Ь > 5. Кроме того. С(5,с) = 12с + 75. следовательно, первые два. слагаемых в Р(Ь, п, с)

положительны.

Далее, при Ь > 7 коэффициент перед п в Р(Ь, п, с) не меньше, нем (—9с2 — 18с + 31)Ь2 + 171с2 +252с, что положительно при с € [0,1]. Аналогично, свободный коэффициент не меньше Ь2с3 + 36Ь2с2 + 108Ь2с + 42Ь2 + 71с3 + 126с2, что также положительно при с € [0,1].

Рассмотрим случай Ь = 5. Р(5,п, с) = 19п3 + (12с—210)п2 + (—108с2 —420с+425)п+24с3 + + 540с2 + 1800с + 750 > (12с + 75)п2 + (—108с2 — 420с + 425)п + 24с3 +

+ 540с2 + 1800с+750 > 75п2 — 103п + 750 > 0. посшэльку п > 3Ь = 15 1і с € [0,1]. Полученный квадратный трехчлен не имеет корней. Рассмотрим случай Ь = 6, Р(5, п, с) = 24п3 — 324п2 + + (—180с2—540с+864)п+60с3 + 1080с2 +3240с+1296 > 108п2 + (—180с2 — 540с+864)п+60с3 + + 1080с2 + 3240с + 1296 > 108п2 + 144п + 1296 > 0. поскольку п > 3Ь = 18 11 с € [0,1]. Полученный квадратный трехчлен также не имеет корней.

Поскольку /3 возрастает на Аь,_п и отрицательна в 1 — Ь/(п + с), /4(г) положительна Аь- Более того, производная (1 — _z)^b^⁵^п-ь-⁴ _п0 ^ _{также поло}жительна на Аь. Таким образом, d ⁴ g/dz ⁴ возрастает на. Аь. и это влечет л"тверждепне 3. □

• 3. Доказательства теорем3.1.    Доказательство теоремы 3

Проинтегрируем функции gt по от резку Аь,_п+_С:

b                 1— ь п+с                 п+с

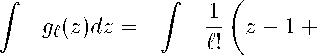
Ь + 1 п + с

1— Д¹           1— ^±1

п+с                 п+с

^ 1+1

Ь +1 п + с

У[ S ( 1

—

Ь +1 п + с

)]

dz =

1 (1+1)

(z — 1 +

1-

п + с

1_— b+1 п + с

[Й (1 — Ь+1 )]dz = dz1 п + с

(I + 1)!(п + с

Таким образом по утверждению 3 получаем

9b,n,c

6 Сс :=Е

1=0

________1________dis

(I + 1)!(n + c)^l+1 Эх ¹

(1 -

Ml) +__ n + c 120(

J___д4д n + c)5 дх4

-

b n + c

)•

Согласно утверждению 1 для доказательства Pb +1 ,_n,_c >  Рь,п,_с достаточно показать, что

/ b +1\V b + 1\ ^n-b , .

(. ..) С^{1 -} nr-)   ^- <- >  "•

Левая часть этого неравенства равна

(^ у ( 1 - ^ -г - +=

=     1     ⁽ b+Іу^{-4 (} ₁ _ b + 1 Y^{- b- 3} _L  - b    Ә ⁴д ⁽ ₁ _ b ^у

24(n + c)7 У + c) У n + c) ^b,n 120(n + c)⁵ дх⁴ У n + c) ¹

где L_b,_n = -24(b+1)4(b-c-n+1)³-b(-24(b+1)³(b-c-n+1)³-12(b+1)2(b-c - n + 1)²(b-c--2n + bc + 1) - 4(b + 1)(b³c² + 4b³c + b³n + 2b³ - b²c³ - b ² c ² n - 6b² c² - 11b²cn + 2b²c - 2b²n²--7b²n + 6b² + 3bc³ + 9bc²n - bc² + 7bcn² + 6bcn - 8bc + bn³ + 10bn² - 17bn + 6b - 2c³ - 8c²n+ +6c² - 11cn² + 17cn - 6c - 5n³ + 12n² - 9n + 2) - b³c³ - 9b³c² - 3b³cn - 18b³c - 7b³n - 6b³+ +6b²c³ + 12b² c²n + 18b²c² + 3b²cn² + 51b²cn - 18b²c + 15b²n² + 15b²n - 18b² - 11bc³ - 36bc²n+ +9bc² - 36bcn² + 3bcn + 18bc - 8bn³ - 24bn² + 51bn - 18b + 6c³ + 24c²n - 18c² + 33cn²--51cn+18c+16n³-39n²+29n-6 ) = 12b⁶c-12b⁶-20b⁵c²-24b⁵cn+100b⁵c+28b⁵n-76b⁵+9b⁴c³+ +20b⁴c²n - 119b⁴c² + 12b⁴cn² - 161b⁴cn + 330b⁴c - 20b⁴n² + 151b⁴n - 202b⁴ + 38b³c³ + 92b³c²n--298b³c² + 61b³cn² - 431b³cn + 546b³c + 4b³n³ - 91b³n² + 321b³n - 294b³ + 75b²c³ + 184b²c²n--337b²c² + 128b²cn² - 511b²cn + 514b²c + 16b²n³ - 140b²n² + 373b²n - 250b² + 46bc³ + 112bc²n--210bc² + 79bcn² - 361bcn + 282bc+12bn³ - 141bn² + 247bn - 118b+24c³ + 72c²n - 72c² + 72cn²-- 144cn + 72c + 24n³ - 72n² + 72n - 24.

Достаточно показать, что b(n + c)2(d4д/дх4) (1 - ^^F)

^L b,n >

5 ( ^+1 ) ^{b 4} ( 1 - ^+1 ) ” ^{b 3} n + c           n + c

5(b + 1)(n + c - b - 1)^'b’n, где Rb,n = b4c4+16b4c3+6b4c2n+72b4c2+40b4cn+96b4c+3b4n2+46b4n+24b4-10b3c4-20b3c3n--80b3c3 - 6b3c2n2 - 198b3c2n - 72b3c2 - 84b3cn2 - 352b3cn + 192b3c - 6b3n3 - 140b3n2--8b3n+96b3+35b2c4 + 120b2c3n+80b2c3 + 132b2c2n2+366b2c2n - 216b2 c2+44b2cn3+492b2cn2--432b2cn+3b2n4+146b2n3-6b2n2-300b2n+144b2-50bc4-220bc3n+80bc3-354bc2n2+198bc2n+ +72bc2-240bcn3+84bcn2+352bcn-192bc-52bn4-74bn3+420bn2-392bn+96b+24c4+120c3n--96c3 +228c2n2-372c2n+144c2+196cn3-492cn2+392cn-96c+65n4-226n3 +283n2-146n+24.

Это неравенство справедливо тогда и только тогда, когда положителен многочлен F (n,b,c) = 5(b + 1)(n + c - b - 1)Lb,_n - bRb,_n = (44b⁵ + 245b⁴ + 530b³ + 655b² + 326b + 120)c⁴+ +(n(145b⁵ + 815b⁴ + 1825b³ + 2305b²’ +1150b + 480) - 1784b - 3770b² - 4425b³ - 2805b⁴ - 991b⁵--145b⁶ - 480)c³ + (3396b - n(320b⁶ + 2286b⁵ + 6787b⁴ + 11111b³ + 9693b² + 4843b + 1440) + +8053b² + 11426b³ + 9712b⁴ + 4858b⁵ + 1355b⁶ + 160b⁷ + n²(160b⁵ + 931b⁴ + 2193b³ + 2869b²+ +1447b + 720) + 720)c² + (n(180b⁷ + 1745b⁶ + 6890b⁵ + 14762b⁴ + 18272b³ + 13613b² + 6218b+ +1440) - 2744b - 7398b² - 12000b³ - 12352b⁴ - 8016b⁵ - 3150b⁶ - 680b⁷ - 60b⁸ + n³(60b⁵ + 385b⁴+ +1001b³ + 1415b² + 739b + 480) - n² (180b⁶ + 1450b⁵ + 4741b⁴ + 8337b³ + 7639b² + 4213b +1440) --480)c + 806b + (20b⁴ + 97b³ + 192b² + 115b + 120)n⁴ - n(200b⁷ + 1475b⁶ + 4691b⁵ + 8302b⁴+ +8990b³+6143b²+2519b+480)+2454b²+4416b³+5104b⁴+3846b⁵+1830b⁶+500b⁷+60b⁸--n³(120b⁵ + 669b⁴ + 1541b³ + 1651b² + 1139b + 480) + n²(240b⁶ + 1547b⁵ + 4210b⁴ + 6036b³+ +5150b² + 2737b + 720) + 120.

Рассмотрим его вторую производную ^Цд?^) = (52865 +280864 +768063 +324062+105126--1728)с2 + (п(87065 + 486664 +1215063 + 723062 +186606 - 3456) - 49446 - 3318062 - 2079063-1779064 - 594665 - 87066 - 2880)с + 70806 - п(64066 + 457265 + 1377864 + 1881463+ +2818262 + 40946 + 2880) + 1308262 + 2688463 + 1812864 + 971665 + 271066 + 32067+ +(32065 + 186264 + 460263 + 35 0662 + 80786 - 1728)п2 + 1440 как многочлен от с при фиксированных п, 6. При 6 > 1 коэффициент перед с2 положителен. По условию утверждения п > 36 + 2, тем самым коэффициент перед с больше, чем 174066 + 865265 + 1866064 + 90063 + 2280062 - 153126 - 28 80. что положіітелыю при 6 > 1. Получаем, что вершина соответствующей параболы находится при отрицательном с, следовательно, при с € (0,1) вторая производная возрастает.

Исследуем на ее значение при с =  0 и 6  >  3. Полу чаем ^д ^д?’^’⁰ )   =

= (32065 + 186264 + 460263 + 35 0662 + 80786 - 1728)п² + (-64066 - 45 7265 - 1377864-1881463 - 2818262 - 40946 - 2880)п + 32067 + 271066 + 971665 + 1812864 + 2688463+ +1308262 + 70806 + 1440. Рассмотрим это выражение как многочлен от п при фиксированном 6. Очевидно, что при 6 > 3 свободный коэффициент и коэффициент перед п² положительны. По условию утверждения п > 36 + 2, тем самым с помощью неравенства п² > 36п и положительности коэффициента перед п² получаем: ^д2Ғ?^ь0 > (32066 +101465 + 2864 - 829663 - 394862 - 92786- 2880)п + 32067 + 271066 + 971665+ +1812864 + 2688463 + 1308262 + 70806 + 1440. При 6 > 3 с помощью неравенства b^k > 3 3 6^k- 3 ,k > 3 получаем, что коэффициент перед п не меньше, чем 34463 + 2343062 - 85226 - 2880 > 0.

Теперь рассмотрим случай 6 = 1, при котором д' Ғд?1’0) = 16640п2 - 72960п + 79360. Корни этого многочлена равны п = 2 и п = 31/13. Поскольку п > 36 + 2 = 5, то многочлен положителен. В случае 6 = 2 по.тучаем. что д Ғд?2’0) = 105 3 00п2 - 682020п + 1098360. Корни этого многочлена равны п = 3 и п = 226/65. Поскольку п > 36 + 2 = 8, то многочлен д2Ғ(n,b,c) _ положителен. 1ем самым доказана положительность второй производной —дс2   ПРИ всех п, 6, с. удовлетворяющих условию п > 36 + 2.

Рассмотрим первую производную при с = 0. Полу чаем: ^дҒ ( g^’⁰ ) = (6065 + +38564 + 10 1 363 + 95162 + 22476 - 576)п³ + (-18066 - 145065 - 475364 - 74 1 363-1122762 - 15376 - 1440)п² + (18067 + 174566 + 689065 + 1429864 + 2116063 + 1079762 + 66106+ +1440)п - 6068 - 68067 - 315066 - 801665 - 1312064 - 1094463 - 759062 - 28406 - 480. Видим, что коэффициенты перед п³ и п положительны. Пусть п > 36 + 5, тогда заменяя п³ и п на п²(36 + 5) и 36 + 5 соответственно, получаем: ^{дҒ (}?С^Ь’ 0) > (565 + 21164 + 50563 + 26962 + 79706 - 4320)п² + 48068 + 545567 + 2624566 + 6932865+ +12185064 + 12724763 + 6622562 + 345306 + 6720 > 0 щ>и 6 > 1.

Отдельно разбирая случаи 36 + 2 6 п < 36 + 5, получаем, что во всех случаях первая производная положительна. Действительно, ^ӘҒ ( ^3Ь + _С²’^Ь’⁰⁾ = 48068 + 334067 +104 1466 +1382465 + 215 1 664 + 3368463 +1491862 - 114886 - 7968. ^дҒ(3b + _c³’^b’⁰⁾ = 48068 + 406067 +1565466 + 30 76265 + 4614864 + 7312863 + 639906² - 44306 - 24672. ^{дҒ (3b} + _c 4 ’^b’⁰⁾ = 48068 +478067 +2161466 +5281065 +8643864+13309863+14817262 +296326 - 54624.

Величина Ғ (п, 6, 0) положительна согласно статье [2].

• 3.2.    Доказательство теоремы 2

Согласно формуле Тейлора с остаточным членом в форме Лагранжа для любого z € [1 - ?и’ 1 - ?+! ] существует d € [0,1]. для ксвторого g(z) = ^3=0 gi(z) + r(z, d), где

r(z, d)

24 G

-1+

6 + 1 п + с

У d4g / dz4 1

-

6 + d п + 1

.

Учитывая полученную ранее формулу

1-

ь п+1

ge(z)dz =

-1 _ ь+1 п+1

______1______dig Д - ь +1 (I + 1)!(п + 1)^l+1 dz^£ п + 1

а также аналогично получаемую

1-m п+1                                 Л

/ ^{r (z}'^d)dz= 120(n¹ +1) 5 О I ¹ - П+1 )

• 1-    ь+1

¹ п+1

согласно утверждению 1 для доказательства рь +1 ,п,с >  рь,п,с достаточно показать, что

/ ь + 1 У / ь + 1 V^-b . Г^1-тт

—ГТ    ¹--ГТ ^{- ь}       g^(z)dz >⁰'

Vп + 1/ к п + 1/        ]-_ М1

п + 1

Расписывая выражение в левой части неравенства, получаем

(У -

7 I 1 \ П-Ь        />1--^

—— )   - ь [   + g(z)dz п + 1/ Ji- m п + 1

= (ь + 1)^b—4(п - ь _{т ( ь d} - ь     д⁴g ⁽ - ь + d \ =

24(п + 1)п W '     120(п + 1)5 dz4 V    п + 1/

(ь + 1)^b—4(п - ь)^п—b—3_т. _k ,.     (ь + d)^b—5(п + 1 - ь - Т^{п b 4}         ,.

=-----24(п + . -----L("'6'd)--120(п + 1)"--------тЛ), где Т(п, ь, d) = 4ь5п+4ь5 -8ь4п2 + 10ь4п+18ь4+4ь3п3-30ь3п2-18ь3п-8ь3 + 16ь2п3-12ь2п2+ +4бь2п+2ь2+12ьп3-62ьп2-2ьп+24п3 и К(п, ь, d) = Ь(3Ь4п2+92Ь4п+209Ь4-40Ь3dп2+24Ь3dп+ +544Ь3d - бь3п3 - 190ь3п2 - 602ь3п - 418ь3 + 6Ь2d2п3 - 222Ь2d2n + 504Ь2d2 + 60Ь2dп3+ +24Ь2dп2 - 852Ь2dп - 81бь2d + 3ь2п4 + 124ь2п3 + 594ь2п2 + 828ь2п + 355ь2 - 8Ьd3п3+ +72Ьd3п2 - 208Ьd3п+192Ьd3-6Ьd2п4-6Ьd2п3+222Ьd2п2-282Ьd2п-504Ьd2 - 20Ьdп4-76Ьdп3+ +372Ьdп2 + 892Ьdп + 464Ьd - 2бьп4 - 224ьп3 - 5Шп2 - 464ьп -1465 + d4п4 - 10d4п3 + 35d4п2 --50d4п + 24d4 + 4d3п4 - 32d3п3 + 68d3п2 + 8d3п - 96d3 + 12d2п4 - 60d2п3 - 12d2п2 + 204d2п+ +144d2 + 24dп4 - 24dп3 - 216dп2 - 264dп - 96d + 24п4 + 96п3 + 144п2 + 96п + 24).

Рассмотрим отношение множителей перед полученными многочленами:

(ь + d)^ь-5(n + 1 - ь - d)"~^b-4 5(ь + 1)^ь-4(п - ь)"^-Ь-3

5(ь + 1)(п - ь)

(г

п

-ь+1-d п - ь

"—b— 4

Поскольку ln(1+ж) 6 ж для любого ж > -1 и еж < 1 + 2ж для любого ж G (0,1), получаем

= exp

/ ь + d\ ь + 1

b-5

п

- ь + 1 -п - ь

п—b— 4

[(ь - 5) log (1

-

1-T) +(п - ь - 4)log f1 + M ь + 1)                V п - ь/J

6 exp

Г- ^{(ь - 5)(1 - d)}

[ ь + 1

+

(п - ь - 4)(1 - d) п - ь

x = п/(Ь + 1) > 1. Сделав замену п = (Ь + 1)x, будем исследовать на неотрицательность многочлен Ғ (Ь, х, d) = Р ((Ь + 1)x, Ь, d) от независимьix переменных Ь Е N, х > 1, d Е [0,1].

Выпишем данный многочлен, сгруппировав слагаемые по Ь: Ғ (Ь, x, d) = (20x4 - 60x3 + 60x2 - 20x)b9+ +(197x4 - 524x3 + 437x2 - 90x - 20)Ь8+

+(6d²x⁴ - 6d ² х³ + 56dx⁴ - 132dx³ + 76dx² + 815х⁴ - 1898х³ + 1275х² - 62x - 130)ь ⁷ + +(-d⁴x⁴ - 76d³x⁴ + 80d 3 x 3 - 150d²x⁴ + 630d²x³ - 480d²x² + 148dx⁴ + 388dx 3 - -1632dx² + 1080dx + 2324х⁴ - 5438х³ + 4035х² - 526x - 369)Ь6+ +(12d5x⁴ + 31d 4 x 4 - 86d4x³ - 212d³x⁴ + 304d³x³ - 72d³x² - 528d²x⁴+ +1152d²x³ - 894d²x² + 510d²x + 8dx 4 + 280dx³ + 2952dx 2 - 5604dx + 1964d + 4374x4 - 7430x3--473x2+6124x-2319)b⁵++(48d⁵x4-120d⁵ x³+134d⁴x⁴-512d⁴x³+829d⁴x²-88d³x⁴+128d³x³+ +1516d³x² - 2456d³x - 492d2x⁴ + 108d²x³ + 1242d2x2 - 6546d²x + 6024d² - 328dx⁴ - 1344dx³+ +292dx2 + 13436dx - 11272d + 4901x4 - 3720x3 - 2692x2 - 3872x + 5099)Ь4+ +(72d5x⁴ - 360d⁵x³ + 420d⁵x² + 206d4x⁴ - 1020d4x³ + 2019d⁴x² - 2446d4x + 248d³x⁴--640d³x³ + 2220d³x2 - 3144d³x + 5856d³ + 102d²x⁴ - 198d²x³ + 810d²x² + 7110d²x - 15840d²--392dx⁴ + 148dx³ - 10644dx²+3220dx + 14404d + 3171x4 - 1814x3 + 6120x2 - 4574x - 4479)Ь³+ +(48d5x⁴ - 360d⁵x³ + 840d5x² - 600d⁵x + 139d4x⁴ - 848d4x³ + 1551d4x²--1700d4x + 2280d⁴ + 292d³x⁴ - 848d³x³ - 396d³x² + 1656d³x - 8448d³ + 354d²x⁴+ +702d2x³ - 3282d2x2 + 8346d²x + 11976d² - 172dx⁴ + 2716dx³ - 1740dx² - 12316dx - 7688d+ +1306x4 - 3198x3 + 3320x2 +4708x + 1874)Ь²+ +(12d5x⁴ - 120d5x³+420d5x² - 600d⁵x + 288d5+ +35d4x⁴ - 254d⁴x³ + 361d⁴x² + 746d4x - 1464d4 + 92d³x⁴ - 304d³x³ - 1028d³x² + 2344d³x+ +2976d³+132d2x4+492d²x³-2436d²x²-5820d²x-3024d²-24dx4+1464dx³+4536dx²+4584dx+ +1536d + 468x4 - 1678x3 - 1882x2 - 1248x - 312)Ь+—+120x4. Обозначим Ғ^ (x,d) — коэффициент в многочлене Ғ(Ь, x,d) перед Ь^к, тем самым Ғ(Ь, x,d) = ^®=о F^ (x,d)b^fc.

Покажем неотрицательность коэффициентов Ғ^ (x, d) или же их комбинаций.

• 1)    Коэффициент F9(x, d) не зависит от d и как многочлен от x имеет корни x = 0 и x = 1 кратности 1 и 3 соответственно. Тем самым F9(x,d) неотрицателен.

• 2)    Коэффициент F8(x,d) не зависит от d и как многочлен от x имеет корни x = 1 кратности 2 и x = 65/197 ± V 8165/197. Тем самым F8(x, d) неотрицателен.

• 3)    Для анализа     F7(x,d)     возьмем его вторую производную

  д²F7/дx² = (72d² + 672d + 9780)x² + (-36d² - 792d - 11388)x + 152d + 2550. Как многочлен от x она достигает минимума при x = (36d² + 792d + 11388)/(144d² + 1344d + 19560) 6 0.6245. В силу того, что коэффициент перед x² положителен, д²F7/дx² возрастает при x > 1, причем д²Ғ7(1, d)/dx² = 36d² + 32d + 942 > 942. Тем с-амым д ² F 7 /Әx ² положительна.

Поскольку дҒ7(1, d)/dx = 6d2 - 20d + 54 > 34, то первая производная тоже положительна. Тем самым Ғ7Д, d) возрастает по x и F7(1,d) = 0, откуда следует неотрицательность Ғ7Д, d).

• 4)    Для анализа     F6(x,d)     возьмем его вторую производную

  д²Ғ б /дР 2 = (-12d⁴-912d³-1800d²+1776d+27888)x²+(480d³+3780d²+2328d-32628)x--960d² - 3264d + 8070. Как многочлен от x она достигает минимума при x = (-480d3-3780d²-2328d+32628)/(-24d4-1824d3-3600d²+3552d+55776) 6 0.6483.

В силу того, что коэффициент перед x2 положителен, д2F6/дx2 возрастает при x > 1, причем д2Ғб(1, d)/dx2 = -12d4 - 432d3 + 1020d2 + 840d + 3330 > 2886. Тем самым д2F6/дx2 положительна.

Поскольку дF6(1,d)/дx = -4d4 - 64d3 + 330d2 - 428d + 526 > 30. то первая производная тоже положительна. Тем самым F6(x,d) возрастает по x и Ғб(1, d) = -d4 + 4d3 - 16d + 26 > 9. откуда следует псотрппатслыіость Ға(т, d).

+1680d — 44580)ж — 144d³ — 1788d² + 5904d — 946. Как многочлен от ж она достигает минимума при ж = (516d⁴ — 1824d³ — 6912d² — 1680d + 44580)/(288d5+ +744d4 — 5088d³ — 12672d² + 192d + 104976) 6 0.5171. В силу того, что коэффициент перед ж² положителен, д²Ғ 5 /дж² возрастает при ж > 1, причем д²F₅(1,d)/дж² = 144d⁵ — 144d4 — 864d³ — 1212d² + 7680d + 6962 >  4742. Тем самым д²Ғэ/дж² положительна.

Поскольку дҒ 5 (1,Ғ)/дж = 48d⁵ — 134d⁴ — 80d³ + 66d² + 1172d + 384 > 170, to первая производная тоже положительна. Тем самым Ғз(ж, d) возрастает по ж и F5(1,d) = 12d⁵ — 55d⁴ + 20d³ + 240d² — 400d + 276. Производная последнего многочлена no d имеет корень ж = 2 кратности 2 и корни ж = —(1 ± V61)/6, следовательно, отрицательна при d Е [0,1], a F5(1,d) убывает на этом отрезке. Поскольку Ғ5(1,1) = 93, получаем неотрицательность Ғ5(ж, d).

• 6)    Коэффициент F4(ж,d) может принимать отрицательные значения. Покажем, что при b >  4 неотрицательна сумма Ғб(ж^)Ь² + Ғ4(ж, d). Ранее было показано, что Ғе(ж, d) неотрицателен, тем самым достаточно показать неотрицательность G(ж,d) = 16F 6 (ж,d) + F₄(ж,d) = 48d⁵ж⁴ — 120d⁵ж³ + 118d⁴ж⁴ — 512d⁴ж³ + 829d ⁴ ж ² — —1304d³ж⁴ + 1408d³ж³ + 1516d³ж² — 2456d³ж — 2892d²ж⁴ + 10188d²ж³ — 6438d²ж² — —6546d²ж+6024d²+2040dж⁴+4864dж³—25820dж²+30716dж—11272d+42085ж⁴—90728ж³+ +61868ж² — 12288ж — 805.

Возьмем его вторую производную д2С/дж2 = (720d5+1980d4—3600d3—12240d2—3840d+ +111300)ж2 + (—720d5 — 3588d4 + 2592d3 + 7560d2 — 6384d — 66900)ж + 1658d4 + 2888d3+ +696d2 + 6488d — 6330. Как многочлен от ж она достигает минимума при ж = (720d5+3588d4—2592d3—7560d2+6384d+66900)/(1440d5+3960d4—7200d3—24480d2 — —7680d + 222600) 6 0.4234. В силу того, что коэффициент перед ж2 по.тожі гтелеи. д2С/дж2 возрастает при ж >    1. причем д2G(1,d)/дж2 = 50d4 + 1880d3 — 3984d2 — 3736d + 38070 > 30350. Тем самым д2С/дж2 положительна.

Первая производная дG(1,d)/дж = — 120d5 + 524d4 + 528d3 — 5640d2 + 9848d — 428. Этот многочлен имеет один корень на отрезке [0.0445, 0.0447], а также по одному корню на отрезках [—4, —3] и [3, 4]. В силу отрицательности старшего коэффициента у первой производной, получаем, что она возрастает, как минимум, при d > 0.0447 и любых ж. Кроме того, многочлен G(1,d) = —72d5 + 435d4 — 836d3 + 336d2 + 528d + 132 имеет единственный корень d > 2, а значит, положителен при 0.0447 6 d 6 1-

Осталось рассмотреть случай d < 0.0447. Исследуем многочлен С(ж, d) на всех отрезках [0, 0.002], [0.002, 0.004],..., [0.042, 0.044], [0.044, 0.0447]. Пусть d Е [Z, г], тогда. £(ж, d) можно оценить снизу многочленом 4-й степени от ж, если в каждом положительном мономе заменить d на Z, а в каждом отрицательном — на г. В ходе исследований установлено, что для каждого отрезка коэффициент перед ж⁴ у таких многочленов положителен, а. наибольший вещественный корень не превосходит 0.982. Тем самым доказано, что многочлен G(ж,d) положителен.

• 7)    Коэффициент Fз(ж,d) также может принимать отрицательные значения. Покажем, что при b > 4 неотрицательна сумма F5(ж,d)b² + Ғз(ж, d). Ранее было показано, что F5(ж,d) неотрицателен, тем самым достаточно показать неотрицательность С(ж, d) = 16Ғ5(ж, d) + Ғз(ж, d) = 264d⁵ж⁴ — 360d⁵ж³ + 420d⁵ж² + 702d⁴ж⁴ — 2396d⁴ж³+ +2019d⁴ж² — 2446d⁴ж — 3144d^4 + 4224d³ж³ + 1068d³ж² — 3144d³ж + 5856d³ — 8346d²ж⁴+ +18234d²ж³ — 13494d²ж² + 15270d²ж — 15840d² — 264dж⁴+4628dж³ + 36588dж² — 86444dж+ +45828d + 73155ж⁴ — 120694ж³ — 1448ж² + 93410ж — 41583.

Возьмем его вторую производную д²С/дж² = (3168d⁵ + 8424d4 — 37728d³ — 100152d² — —3168d+877860)ж²+(—2160d⁵ —14376d4+25344d3+109404d²+27768d—724164)ж+840d⁵+

+4038d4+2136d3 — 26988d2 + 73176d — 2896. Как многочлен от x она достигает минимума при x = (2160d5+14376d4—25344d3 —109404d2—27768d+724164)/(6336d5 + 16848d4— —75456d3 — 200304d2 — 6336d + 1755720) 6 0.5026. В силу того, что коэффициент перед х2 положителен, д 2G/дx2 возрастает при х >  1, причем д2G(1, d)/дx2 = 1848d5 — 1914d4 — 10248d3 — 17736d2 + 97776d + 150800 > 120902. Тем самым д2G/дx2 положительна.

Получаем, что первая производная возрастает и дG(1, d)/дx = 816d5—2788d4—912d3+ +9600d2 — 440d + 21052    >    16912. Таким образом, первая про изводная положительна. Покажем неотрицательность многочлена G(1,d) = 324d5 — 2121d4 + 4860d3 — 4176d2 + 336d + 2840. Его производная имеет корень d = 2 кратности 2, а также корни d = (167 ± V24109)/270, лежащие на отрезках [1.1,1.2] и [0.04, 0.05]. Таким ouptгзом. корень d = (167 — Д24109)/270 является точкой локального максимума. Поскольку G(1, 0) = 2840 и G(1,1) = 2063, получаем, что G(x, d) положительна.

• 8)    Для анализа     F₂(x, d)     возьмем его вторую производную

  д^/дx² = (576d⁵ + 1668d⁴ + 3504d³ + 4248d² — 2064d + 15672)x² + (—2160d⁵ — 5088d⁴— —5088d³+4212d2+16296d—19188)x+1680d⁵+3102d⁴—792d³—6564d²—3480d+6640. Как многочлен от x она достигает минимума при x = (2160d⁵ + 5088d4+ +5088d³ — 4212d2 — 16296d + 19188)/(1152d⁵ + 3336d⁴ + 7008d³ + 8496d² — 4128d + 31344). Покажем, что знаменатель точки минимума больше числителя. Их разность равна —1008d⁵ — 1752d⁴ + 1920d³ + 12708d² + 12168d + 12156. Этот многочлен имеет единственный корень d > 2, тем самым он положителен при d € [0,1], а значит, точка минимума второй производной x < 1. В силу того, что коэффициент перед x² положителен, д²F2/дx² возрастает при x > 1, причем д²F₂(1,d)/дx² = 96d⁵ — 318d⁴ — 2376d³ + 1896d² + 10752d + 3124 >  430. Тем самым д²F2/дx² положительна.

Первая производная дF2(1,d)/дx = 192d5 — 586d4 — 512d3 + 5304d2 — 8336d + 6978 имеет единственный корень d < —2 и положительный старший коэффициент, тем самым она тоже положительна при d € [0,1]. Получаем, что F2(x, d) возрастает по x и F2(1, d) = —72d5 + 1422d4 — 7744d3 + 18096d2 — 19200d + 8010. Этот многочлен имеет единственный корень d > 10 и отрицательный старший коэффициент. Тем самым показано, что F2(x, d) положительна.

• 9)    Коэффициент Fi(x,d) может принимать отрицательные значения. Покажем, что при 6 > 4 неотрицательна сумма F2(x,d)6 + F/x,d). Ранее было показано, что F2(x,d) неотрицателен, тем самым достаточно показать неотрицательность G(x,d) = 4F2(x,d)+Fi(x,d) = 204d5x⁴—1560d5x³+3780d5x²—3000d⁵x+288d⁵+591d⁴ x⁴— —3646d4x³ + 6565d4x² — 6054d4x + 7656d⁴ + 1260d³x⁴ — 3696d³ x³ — 2612d³x2 + 8968d³x— —30816d³ + 1548d2x⁴ + 3300d²x3 — 15564d2x² + 27564d2x+44880d² — 712dx⁴ + 12328dx³ — —2424dx2 — 44680dx — 29216d + 5692x4 — 14470x3 + 11398x2 + 17584x + 7184.

Возьмем его вторую производную д2G/дx2 = (2448d5 + 7092d4 + 15120d3 + 18576d2 — —8544d+68304)x2 + (—9360d5 — 21876d4—22176d3 + 19800d2 + 73968d—86820)x+7560d5+ +13130d4—5224d3—31128d2—4848d+22796. Как многочлен от x она достигает минимума при x = (9360d5 + 21876d4 + 22176d3 — 19800d2 — 73968d + 86820)/(4896d5 + 14184d4+ +30240d3  +  37152d2  —  17088d +  136608). Покажем. что знаме натель точки минимума больше числителя. Их разность равна —4464d5 — 7692d4+8064d3 + 56952d2+56880d+49788. Этот многочлен имеет единственный корень при d > 2, тем самым он положителен при d € [0,1], а значит, точка минимума x < 1. В силу того, что коэффициент перед x2 положителен, d2G/dx2 возрастает при x > 1, при чем д 2G(1, d)/dx2 = 648d5 — 1654d4 — 12280d3 + 7248d2 + 60576d + 4280. Этот многочлен имеет два корня, больших 2, и один отрицательный корень. Тем самым д2F2/dx2 положительна в силу положительности старшего коэффициента.

Первая производная dG(1, d)/dx = 696d5 — 1498d⁴ — 2304d³ + 12528d2 — 15392d +19738 имеет единственный корень d <  —2, тем самым она тоже положительна при d Е [0,1] в силу положительности старшего коэффициента. Получаем, что G(x,d) возрастает по x и G(1, d) = —288d⁵ + 5112d⁴ — 26896d³ + 61728d² — 64704d + 27388. Этот многочлен имеет единственный корень d > 10. Тем самым показано, что G(x, d) положительна.

• 10)    Коэффициент F o (x, d) = 120x4 положит елей при x > 1.

Ранее из рассмотрения исключены случаи b Е {1, 2, 3}. Рассмотрим их далее.

• 1)    Для анализа      F (1,x,d)     возьмем его вторую производную

  d²F/dx² = (2304d⁵+6528d⁴+3072d³ —6912d² — 8448d+212352)x2 + (— 5760d 5 — 16320d⁴— —7680d³+17280d2+21120d—154560)x+3360d5+9520d4+4480d3—10080d²—12320d+20400. Как многочлен от x она достигает минимума при x = (5760d⁵ + 16320d⁴ + 7680d³ — —17280d² — 21120d + 154560)/(4608d5 + 13056d⁴ + 6144d³ — 13824d² — 16896d+ +424704) 6 0.4678. В силу того, что коэффициент перед x² положителен, d²F/dx² возрастает при x > 1, при чем d²F (1,1,d)/dx² = —96d⁵ — 272d⁴ — 128d³+ +288d² + 352d + 78192 > 77696. Тем самым d²F/dx² положительна.

Поскольку dF(1,1,d)/dx = 48d5 + 136d4 + 64d3 — 144d2 — 176d + 14344 > 14024, то первая производная тоже положительна. Тем самым F(1,x,d) возрастает по x и F(1,1,d) = 1920, откуда следует неотрицательность F(1,x,d).

• 2)    Для анализа     F(2, x, d)     возьмем его вторую производную

  d²F/dx² = (23328d⁵+64152d⁴ —116640d³ —373248d²+93312d+6765120)x2 + (—38880d⁵ — —138024d⁴ + 46656d³ + 482112d2 + 62208d — 6502680)x + 15120d⁵ + 72684d⁴ + 72144d³ — —101952d² — 157248d + 1128600. Как mho гочлен от x она достигает минимума при x = (38880d⁵ + 138024d⁴ — 46656d³ — 482112d2 — 62208d + 6502680) / (46656d⁵ + 128304d⁴— —233280d3 — 746496d² + 186624d + 13530240) 6 0.5322. В силу того, что коэффициент перед x² положителен, У²F/dx² возрастает при x > 1, причем d²F(2,1,d)/dx² = —432d⁵ — 1188d⁴ + 2160d³ + 6912d² — 1728d + 1391040 > 1387692. Тем самым d²F/dx² положительна.

Поскольку dF(2,1, d)/dx = —144d5 + 180d4+3456d3 +4896d2 — 4608d+171180 > 166428. то первая производная тоже положительна. Тем самым F(2, x, d) возрастает по x и F(2,1,d) = 16200. откуда следует псотрппатслыюсть F(2, x, d).

• 3)    Для анализа     F(3,x,d)     возьмем его вторую производную

  d²F/dx² = (110592d⁵ + 294912d⁴ — 1253376d3 — 3096576d² + 2322432d + 80658432)x2+ +(—138240d⁵ — 589824d⁴ + 700416d³ + 4423680d² — 82944d — 89542656)x + 40320d5+ +273408d⁴ + 317184d³ — 963072d² — 1143936d + 19269120. Как миогочлен от x она. достигает минимума при x = (138240d⁵ + 589824d⁴ — 700416d³ — 4423680d² + 82944d+ +89542656)/(221184d5 + 589824d⁴ — 2506752d³ — 6193152d² + 4644864d+ +161316864) 6 0.5920. В силу того, что коэ(|>(|>ппііепт перед x² по.тожііте.теи. d ² F/dx ² возрастает при x > 1. пріінем d²F(3, 1,d)/dx ² = 12672d⁵ — 21504d⁴ — 235776d³+ +364032d² + 1095552d + 10384896 > 10127616. Тем еамым d²F/dx² положительна.

• 3.3. Доказательство теоремы 4

Поскольку dF (3,1, d)/dx = 864d⁵—2304d⁴—12288d³+59904d2+92448d+970368 > 955776. то первая производная тоже положительна. Тем самым F(3,x,d) возрастает по x и F(3,1,d) = 78720. откуда следует псотрппатслыюсть F(3, x, d).

Согласно формуле Тейлора с остаточным членом в форме Лагранжа для любого г Е [1 — ^, 1 — ^j существует d Е [0,1]. для ксіторого g(z) = ^3=о ді(г) + r(z, d), где r(^,d) = ^ f^—1+)4 д4| <1 — b+d).

24 у п + с    ог ⁴ у п + с

Согласно утверждению 1 неравенство рь+1,_п,_с >  Рь,п,с эквивалентно

/£ УО- —

b + 1

п + с

п-b      ,1 Ь-

I п+с

• — b         g(z)dz >  0,

1-Ml п + с

Выражение в левой части равно

ь п+с

g(z)dz = ь+1

п+с

(b ±1)^Ь-5(п + с — b — 1)^n-b-4     ,    .

--------------------.--------г----------------Р(п, b, с, d), 120(п + с)^п               v , , , у,

/»±1 у Л - y±t)"-^b - b Ғ

Vп ± с} у п ± с}       J __ где Р(п, b, с, d) = (20b4±97b3±6b2d2±20b2d±166b2 — bd4—4bd3 — 12bd2 — 24bd±156b±120)п4± ±(480с — 1365b ±839Ьс ±96bd ±1303Ь2с ±1013b3 с ±385Ь4с ±60Ь5с ±84bd2 — 8b2d ±36bd3 — 48b3d± ±10bd4 — 1629b2 — 1487b3 — 669b4 — 120b5 — 18b2d2 ± 4^243 — 6b3 d2 ± 24b2сd2 ± 4b2сd3 — —72bсd — 24Ьс42 ± 84Ь2с4 — 4Ьс43 — 12Ь3с4 — 480)п3 ± (—180b6с ± 240b6 ± 160b5с2 — 1450Ь5с± ±1547b5 ± 931Ь4с2 ± 12b4с4 — 4753b4с ± 28b4 d ± 4182b4 — 6b3 с2 d2 — 36b3с24 ± 2235b3с2 — —24Ь3с42 — 108b3с4 — 8205b3с ± 30b3d2 ± 120b3d ± 5886b3 ± 18b2с242 ± 108b2с24 ± 2743b2с2 — —36b2с43 — 144b2с42 — 192Ь2с4 — 7267Ь2с — 36b2d3 — 96b2d2 — 288b2d ± 5570b2 — 12Ьс242 — —72Ьс24 ±1531Ьс2 ±36Ьс43 ±168Ьс42 ±288Ьс4—4705Ьс—35bd4 — 104bd3 — 144bd2 ±3020b ± 720с2 — —1440с ± 720)п2 ± (180Ь7с — 200b7 — 320Ь6с2 ± 1745Ь6с — 1475b6 ± 145Ь5с3 — 2286b5с2± ±6890Ь5с — 4691b5 ± 4Ь4с34 ±811b4 с3 ± 36b4 с2 d — 6823Ь4с2 ± 24b4 с4 ± 14738b4 с — 88b4d — 8214b4— —24Ь3с34 ± 1849Ь3с3 ± 42Ь3с242 ± 36Ь3с24 — 11189Ь3с2 ± 168Ь3с42 ± 552Ь3с4 ± 17552Ь3с± ±12b3d2 ± 288b3d — 9290b3 ± 44b2с3d ± 2261b2с3 — 126b2с2d2 — 360b2с24 — 9207b2с2 ± 104b2с43± ±120Ь2с42 — 576b2с4 ± 13965Ь2с ± 104b2d3 ± 288b2d2 — 6535b2 — 24Ьс34 ± 1174Ьс3 ± 84Ьс242± ±288Ьс24—5215Ьс2 — 104Ьс43 — 288Ьс42 ±6610Ьс ±50bd4 ±96bd3 — 2665Ь±480с3 — 1440с2 ± 1440с— —480)п — 60b8с ± 60b8 ± 160b7с2 — 680b7с ± 500b7 — 145b6с3 ± 1355b6с2 — 3150b6с ± 1830b6± ±44Ь5с4 — 991b5с3 ± 4858b5с2 — 8016Ь5с ± 3846b5 ± 245Ь4с4 — 16Ь4с34 — 2789Ь4с3 — 144Ь4с24± ±9856Ь4с2 — 288Ь4с4 — 12064Ь4с — 96b4d ± 5200b4 ± 530b3с4 ± 96b3с3d — 4521b3с3 — 72Ь3с242± ±432Ь3с24 ± 11066Ь3с2 — 288Ь3с42 ± 288Ь3с4 — 12000Ь3с — 144b3d2 ± 4560b3 ± 655b2с4— —176Ь2с34 — 3594Ь2с3 ± 216Ь2с242 — 288Ь2с24 ± 8125b2с2 — 96Ь2с43 ± 288Ь2с42 — 7590Ь2с— —96b2d3 ± 2550b2 ± 326Ьс4 ± 96Ьс34 — 1880Ьс3 — 144Ьс242 ± 3540Ьс2 ± 96Ьс43 — 2840Ьс — 24bd4± ±830b ± 120с4 — 480с3 ± 720с2 — 480с ± 120. Тем самым знак полученного выражения полностью определяется знаком многочлена Р(п, b, с, d).

Поскольку b € (еп, п), то при п ^ ±то многочлен Р(п, b, с, d) асимптотически эквивалентен Ь ⁴ п ⁴ Н (b/п), где Н (ж) = 20 ± (60с — 120)ж ± (—180с ± 240)ж² ± (180с — 200)ж³± ±(—60с ± 60)ж⁴. то есть сумме слагаемых с маіеспмальной суммарной степепьто b іі п. Многочлен Н (ж) имеет корень ж = 1 кратности 3 и корень ж = 3(₁1__с) • Тем самым асимптотически смена знака происходит при b = 3(1 ^П _с) •