Морфизм между планируемыми рисками судовой операции и рисками при ее реализации

В современных условиях обеспечение безопасного мореплавания ориентировано на использование метода программно-целевого управления. При таком управлении состоянием безопасности мореплавания судов две последовательные фазы алгоритма этого метода – планирование и реализация – могут быть связаны морфизмами. Действительно, с одной стороны, система планирования и система реализации объединены целью судовой операции, а с другой стороны, планирование операции осуществляется в закрытой системе, а реализация – в открытой системе. Поэтому с практической точки зрения особенно важным является анализ возможности перерасчета апостериорных (допустимых) рисков, закладываемых на этапе планирования операции, в предвычисленные текущие риски, которые будут и должны возникать в процессе реализации плана этой судовой операции [1]. Иными словами, существует необходимость в оценке вероятности события вида ω ≥ ω ₀ , где ω – некоторый продолжительно действующий случайный параметр опасности, например риск, определяющий навигационное состояние судна в фиксированный момент времени при реализации операции (Ρ(ω ≥ 0) = 1); ω ₀ – априорно заданная величина приемлемого риска, которая гарантирует нужный уровень безопасности мореплавания в фазе планирования такой операции. Условие Ρ(ω ≥ ω 0 ) отражает возможность доминирования текущего предвычисленного риска над плановым допустимым риском, что будет снижать уровень безопасности мореплавания судна [2–4].

Материалы и методы

Мореплавание всегда сопряжено с риском, который в той или иной степени сопровождает судно. Нет возможности в каких-либо абсолютных единицах оценить степень риска во время судовождения, но можно и необходимо говорить об относительной его величине [5].

Всякое изменение обстановки по отношению к исходной позиции повышает степень риска и требует от судоводителя активных и грамотных действий, направленных на обеспечение безопасности мореплавания. Чем сложнее создается ситуация, тем больше требуется действий, которые бы "компенсировали" возникающую угрозу.

Целью планирования навигационного маршрута (перехода) является разработка способов и методов плавания судна с учетом сложных и опасных навигационных ситуаций, которые могут встретиться в любой момент времени и любых координатах составляемого перехода [6].

Навигационное планирование маршрута перехода в заданный порт или район промысла является важнейшим этапом подготовки, включает анализ всех обстоятельств, сопутствующих переходу, и сбор доступной судоводителю информации, имеющей отношение к навигационным и гидрометеорологическим условиям плавания.

Для оценки перехода и обстоятельств, при которых данный переход будет выполняться, должна быть собрана полная информация:

• 1)    о гидрометеорологических условиях плавания (видимости, туманах, господствующих ветрах, штилях и штормах, постоянных и дрейфовых течениях, приливах и приливоотливных течениях, ледовой обстановке и т. д.);

• 2)    навигационной обстановке перехода (общей длине пути, характеристике береговой черты, надводных и подводных опасностях, запретных и опасных районах, СНО, приметных пунктах и радиолокационных объектах, условиях подхода к портам захода и якорным стоянкам, портовых правилах и т. д.).

Навигационное планирование маршрута перехода включает также:

• –    подбор необходимых карт, планшетов, пособий для плавания и промысла, их корректуру;

• –    предварительную прокладку маршрута перехода на обзорной (или генеральной) карте, охватывающей весь район плавания (на карту наносятся предполагаемый маршрут перехода и обобщенные результаты изучения навигационно-гидрографических и географических условий: районы, имеющие ограничения по режиму плавания; границы территориальных вод; зоны или линии равных точностей определения места судна с помощью различных средств; положение и данные береговых радиотехнических средств, а также другие необходимые для судовождения сведения);

• –    детальную предварительную прокладку частей маршрута перехода, пролегающих через прибрежные воды, на путевых, частных картах и планах, а также "подъем" этих карт – нанесение на них дополнительной навигационной информации и выделение сведений, имеющих значение для обеспечения безопасности и соблюдения правил плавания;

• – анализ навигационной, гидрометеорологической и правовой обстановки, состояния сырьевой базы в районе промысла с целью выбора мест лова (промысловых площадок), поисковых и промысловых курсов, средств и способов навигационного обеспечения промысла;

  – предварительную подготовку промыслово-навигационных планшетов или карт, нанесение условных мест навигационных ориентиров, находящихся за рамками планшета, сеток изолиний, границ промысловых площадок, в пределах которых с заданной вероятностью обеспечивается удержание судна, буксирующего трал, схем расположения поисковых и промысловых курсов;

  – составление штурманской справки, содержащей справочный материал по районам плавания и промысла, который нельзя было нанести на карты, описание маршрута перехода, а также краткое обоснование выбора путей, мест лова, поисковых и промысловых курсов, средств и методов навигационного обеспечения перехода и промысла с оценкой точности плавания.

Эффективное навигационное планирование перехода – важнейший элемент общей организации штурманской службы. Именно так определяется планирование предстоящего рейса судна в Резолюции ИМО A 285(VIII), позднее закрепленной в Международной конвенции ПДНВ – 78/95 [7].

Результаты и обсуждение

Оценка вероятности доминирования текущего риска над величиной приемлемого риска

Пусть задано множество ω ∈ Ω с ограничениями, которые накладываются на плотности распределения вероятности элементов ω, причем действует как основное ограничение вида

/(to) > 0, J/(®)dto = 1, так и дополнительные ограничения, заданные как

f(ω) ≤ c, f′(ω) ≤ 0,

∞ j tof (o)d to = m.

В достаточно общем случае ограничения, наложенные на плотность распределения вероятности величин рисков, можно записать так:

J 9i (to) f (to)dto = mi,

{f(ω), f′(ω)} ⊂ F,(2)

где m i – заданное число; ϕ i (ω) – заданные интегрируемые с весом f(ω) функции; F – некоторая область возможных значений функций f(ω), f′(ω). Тогда задача по оценке вероятности события ω ≥ ω 0 будет состоять в том, чтобы при условиях (1) и (2) найти максимум вероятности

Ρ(ω ≥ ω0),(3)

где ω – некоторое число, и функцию плотности вероятности f ⁰ (ω), обеспечивающую искомый максимум.

Запишем вероятность (3) в виде следующего функционала:

∞

P(to>to0) = j1[to-to0)/ (to)d to, где 1[ω – ω0) – смещенная единичная ступенчатая функция, равная нулю при ω < ω0 и равная единице при ω ≥ ω0.

Таким образом, поставленная задача по оценке вероятности события вида ω ≥ ω 0 может быть сведена к отысканию максимума функционала (4) при выполнении условий (1) и (2). Эта задача может быть сведена к задаче определения максимума для функционала

I _x = J 1[ ®-® 0 ) f ( ® ) d ® + £ X i j ф _i ( ® ) f ( to ) d rn = J T ( го , X ) f ( & )d го                     (5)

₀                                      i = 1      _{0                                0}

при ограничениях (2) и заданных коэффициентах Лагранжа λ i , i = 1, l. Кроме того, в принятом функционале функция ψ(ω 0 , λ) определяется так:

l

T(rn, X) = 1[m - to o ) + £ X i ф i (m).

i = 1

Максимуму функционала (5) соответствует функция f0(ω, λ), удовлетворяющая при каждом ω условию max [ψ(ω, λ) f(ω)] = ψ(ω, λ) f0(ω, λ).                                    (6)

Условие (6) имеет конечное или бесконечное число решений, если ψ(ω, λ) ≠ 0, а в особых случаях, когда ψ(ω, λ) = 0, уравнение (6) решения не имеет. Определив функцию f ⁰ (ω , λ) и значение λ 0 параметра λ, удовлетворяющего условию (1), можно записать решение поставленной задачи следующим образом:

∞ f 0 (to) = f 0 (to, x), P (to > too ) = J f 0 (to)dto.

Таким образом, процедура предлагаемого метода определения максимума Ρ(ω ≥ ω 0 ) и соответствующей этому максимуму функции f ⁰ (ω) позволит оценить вероятность свойства доминирования текущего риска над величиной приемлемого риска и упростить процедуры управления состоянием мореплавания и эксплуатацией судна в целом [8].

Оценка величины текущего навигационного риска по заданной величине приемлемого риска

Как следует из общего описания метода определения максимума Ρ(ω ≥ ω 0 ), функция f ⁰ (ω) существенно зависит от исходных условий (1), (2). Для получения практических оценок примем, что случайная величина риска ω ∈ Ω обладает математическим ожиданием m. Наличие математического ожидания на множестве рисков Ω позволяет конкретизировать условия (1) и (2), представив их так:

ϕ 1 (ω) ≡ 1, m 1 = 1, ϕ 2 (ω) = ω, m 2 = m, l = 2, f(ω) ≥ 0;                           (7)

∞∞ j Ф1 (to) f (o)drn = m1,   j ф2 (to) f (a)drn = m2,                                  (8)

Для уточненных начальных условий функционал (5) можно записать

∞ ix = j {i[to-®0) + x1 +x 2®} / (®)d®. 0

В связи с тем что условие (7) не ограничивает функцию сверху, эта функция может принимать бесконечные значения. Из первого уравнения (8) следует, что f(ω) не может принимать бесконечные значения на множестве значений ω положительной меры. Следовательно, значение параметров λ 1 , λ 2 , при которых функция

ψ(ω, λ) = 1[ω – ω0) + λ1 + λ2ω положительна на множестве значений ω положительной меры, рассматривать не нужно. Значения параметров λ1, λ2, при которых функция ψ(ω, λ) отрицательна на 0 ≤ ω < ∞, также не следует рассматривать, так как в этом случае из условия (6) следует f0(ω, λ) = 0, а это противоречит условию (8). Значит, следует рассматривать только значения λ1 = 0, λ2 = –1/ω0, при которых функция f0(ω, λ) равна нулю при всех значениях ω, кроме двух: ω = 0 и ω = ω0. В этих точках функция f0(ω, λ) не определяется условием (6). Учитывая условие (7), принимаем функцию f0 в виде f0(ω, ν) = ν1δ(ω) + ν2δ(ω – ω0), где ν1, ν2 – неопределенные неотрицательные множители, которые можно определить из условия (8). Подставив последнее выражение в формулу (8), получим

ν1, + ν2 = 1, ν2ω0 = m или

ν 2 = m/ω 0 ν 1 , = 1 – m/ω 0 .

Следовательно, искомая функция f0(ω) имеет вид f0(ω) = (1 – m/ω0) δ(ω) + m/ω 0(δ(ω – ω0)),                                 (9)

и так как ν1 ≥ 0, то функция (9) справедлива, если ω ≥ m. Плотности вероятности (9) соответствует случайная величина с двумя возможными значениями ω = 0 и ω = ω0. Тогда максимум вероятности (3) можно определить как max Ρ(ω ≥ ω0) = ∫f0(ω)dω = m/ω0 при ω ≥ m или

Ρ(ω ≥ ω 0 ) = m/ω 0 при ω 0 ≥ m.                                  (10)

Полученное неравенство является неравенством Чебышева [4], для которого при f(ω) = f ⁰ (ω) неравенство (10) превращается в равенство, а при f(ω) ≠ f ⁰ (ω) на множестве ненулевой меры следует использовать только строгое неравенство. Кроме того, неравенство обеспечивает возможность оценивать величину текущего навигационного риска по заданной величине приемлемого (апостериорно заданного) риска.

Соответствие между планированием судовой операции P ₁ и процессом реализации этого плана P ₂ по параметрам угроз – рискам

Неравенство, связывающее допустимый и текущий риски (10), позволяет, ориентируясь на теорию категорий, найти соответствия между планированием судовой операции P ₁ и процессом реализации этого плана P ₂ по параметрам угроз – рискам. Для этой цели введем категорию соответствий следующим образом. Пусть Q = (F, R, P) являются объектами категории, где F – количество пар (R, P) – "риск – операция". Тогда отображения вида

φ 1 : ω 0 → ω, φ 2 : P 1 → P 2

можно считать морфизмом соответствия Q ₁ = (F ₁ , ω ₀ , P ₁ ) в соответствие Q ₂ = (F ₂ , ω, P ₂ ), если будет справедливо соотношение

φ* 2 ○ Q 1 ⊂ Q 2 ○ φ* 1 ,                                         (11)

где знак "○" обозначает композицию соответствий, а φ* i = 1, 2 – распространение отображений φ i на множество подмножеств. Соотношение (11) можно представить графически в виде диаграммы (рис.).

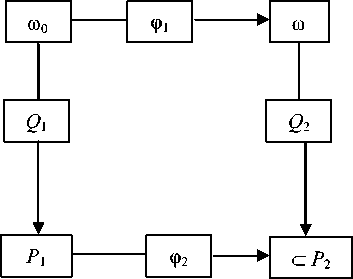
Рис. Fig.

Указанное соотношение (11) можно также формально записать следующим образом:

(φ 1 φ 2 )

Q1 → Q2, причем в последнем выражении стрелка означает морфизм в категории соответствий [9]. Допущения (1) и (2), а также неравенство (10) с учетом выражения (11) позволяют найти соответствие между планированием судовой операции и процессом реализации этого плана в рамках отношений морфизмов по параметрам угроз – рискам, которые будут определяться в интервале от величины ω до величины ω0.

Заключение

При обеспечении безопасности мореплавания судов две последовательные фазы алгоритма программноцелевого управления состоянием судна – планирование и реализация – связаны полной группой изоморфизмов. Поэтому полученное неравенство позволяет осуществлять перерасчет оценок приемлемых (апостериорно заданных) рисков, закладываемых в план судовой операции, в оценки текущих навигационных рисков, что обеспечивает поддержание безопасности мореплавания при реализации этой операции. Кроме того, морфизмы, обеспечивающие соответствие между планированием судовой операции и процессом реализации плана, и ограничения, накладываемые на множество рисков, позволяют найти интервал, в котором будут реализовываться данные риски при выполнении судовой операции.