Морфометрические параметры речного русла в модели плоскопараллельного течения

Процессы хозяйственного освоения природных ресурсов распространились на большую часть речных бассейнов. Часто они приводят к ухудшению экологического состояния региона, которое может на многие годы выйти из состояния биологического равновесия. Загрязнение природных вод продуктами ускоренной эрозии на водосборах дополняются физико-химическими и биологическими загрязнениями техногенного воздействия. Для оценки воздействия хозяйственной деятельности на баланс веществ необходимо изучение количественных закономерностей распространения в водном потоке различных загрязняющих субстанций.

Речной поток практически никогда не бывает представленным одним руслом. Всегда имеются пересекающиеся друг друга сети речных русел. При образовании из двух водных потоков одного изменяются русловые характеристики, загрязнение и минерализация общего водотока. Внутригодовая динамика стока, смена морфодинамического типа русла влияют на изменение экосистемы водных потоков. Оно связано со сложными процессами изменения всех гидравлических и морфометрических характеристик системы поток-русло. В ча стности, динамика стока контролируется вариацией уклонов водной поверхности, скорости течения и глубины потока. Морфометрические параметры водотока влияют на активность водообмена. В свою очередь водообмен определяет минерализацию, кислотно-щелочные и окислительно-восстановительные условия речного русла.

Обычно измеряемыми величинами являются следующие: расход воды Q (м^э/с), средняя скорость течения реки V (м/с), концентрация С (мг/л) растворенного компонента. Течение реки характеризуется шириной Н и глубиной h русла, а также перепадом давления ДР на длине L, которое, собственно, и вызывает само течение. Поэтому представляет интерес выявление связи между регулярно измеряемыми концентрациями компонентов водного массы и характеристиками русла реки.

Цель настоящей работы является установление связи морфометрических параметров русла реки в приближении открытого стационарного потока и сезонной зависимости макрокомпонентов. Изменение морфометрических параметров русла приводит к изменению гидрологических условий, которые непосредственно влияют на водообмен. Изменение водообмена неминуемо приводит к сдвигу карбонатно- кальциевого равновесия. Расчеты проводятся в приближении плоскопараллельного течения на примере р. Чикой и ее притока р. Киран. Между створами с. Поворот (устье р. Чикой) и с. Чикой (верховье) впадает приток река Киран. Расстояние между створами 140 км (рис.1). Ширина р. Чикой на рассматриваемом участке изменяется в пределах от 250 до 260 м. Глубина варьирует от 5 до б м. Река Киран имеет ширину 30 м и глубину 2 м.

Плоскопараллельное течение

Минерализация вод р. Чикой на створе с. Чикой не превышают 0,1 г/л в течение года. Ниже по течению р. Чикой на створе с. Поворот минерализация повышается на 15-20 %. Отличием по сравнению с р. Чикой вод притока р. Киран является повышенная минерализация (0,25 г/л). Обладая повышенной минерализацией, воды р. Киран являются причиной загрязнения вод р, Чикой. В месте слияния реки и притока, которую назовем ближней зоной, наблюдается ареал загрязнения, который распространяется вниз по течению [1]. В результате диффузии и турбулентности область смешения и разбавления речных вод распределяется по всей водной массе, образуя дальнюю зону. Это обстоятельство позволяет для моделирования характеристик русла водного стока использовать двумерную модель течения водной массы без учета вертикального градиента.

При двумерном описании водного потока русло реки ограничим параллельными берегами шириной Н. Ось х направим вниз по течению вдоль одного из берегов, а ось у нормально к противоположному берегу. Скорость водного потока направлена вдоль оси х и зависит только от координаты у, т.е. вектор скорости Г = (Г (у).0.0). В пренебрежении посторонними субстанциями течение воды определяется уравнением Навье-Стокса [3]:

д У -    - VP л

---+ (Г-7) У = --+ -2- V²y. (1) 5 /                р р

Здесь используются стандартные обозначения: V - оператор Набла, р - плотность жидкости (10 3 кг! м 3), т) - вязкость воды ПО 'Зкг!м-с\. Для стационарного двумерного медленного течения воды между двумя плоскими параллельными берегами уравнение Навье - Стокса (1) принимает вид:

d ² V, _ ДР d у ² г) L

Здесь ДР - перепад давления на длине L . Интегрируя уравнение (2) с учетом естественных граничных условий - обращения в нуль скорости на берегах, получаем

Ян-у\ (3)

2 л L

Это известный параболический профиль.

Используя решение (3), найдем среднюю скорость течения реки и расход воды. По определению средних, имеем:

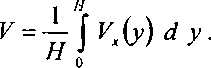
Подставляя (3) и производя элементарное интегрирование, получаем среднюю скорость;

Поток воды Q = J У, (у) d А , где А - поперечное сечение русла реки. Представим d А как h d у, где И - глубина реки, тогда

н

о

Подставляя (3), окончательно находим

0 = ^ ИН³. (5) П н L

Этот результат заменяет известную формулу Пуазейля для течения по трубе [3]. Фактически, результат (5) является первым неисчезающим членом ряда по малому параметру hl Н, получающемуся при решении трехмерной задачи течения водной массы.

Используя (4) и (5), можно получить следующую полезную формулу для расхода воды:

Q = VhH. (6)

Эта формула точная в том смысле, что является определением средней скорости.

Выразим ширину реки и ее глубину через измеряемые величины - расход воды и ее средней скорости. Из (4) сначала находим

Н = ВУ^и\        (7)

где для краткости записи формул ввели а затем из (6):

Проверка формул, полученных в предположении двумерного течения, была проведена для реки Никой на участке створ с.Поворот- с.Чикой. Результаты расчета приведены в табл. 1, где строки V и Q - измерения, а Н / В и В h - вычисленные по формулам (7) и (8). Перемножая У, Н / В и В h получаем, согласно (6), расход воды 2, значения которой в целом согласуются с измеренными значениями.

Оценка сезонной зависимости растворенных веществ

В дальней зоне, где процессы смешения и разбавления не столь существенны, устанавливается стационарный поток, в котором становится возможным пренебречь взаимодействием компонентов водного раствора. В этом случае каждую минерализующую компоненту можно рассматривать независимо друг от друга. Это позволяет составить баланс веществ следующим образом.

Если С - концентрация компонента (мг/л), 5 - поток жидкости, то число молекул рассматриваемой компоненты, проходящих через поперечное сечение в единицу времени, будет пропорционально произведению С Q. Часть из них будет высаживаться из водного раствора на дно водоема, площадью L Н, и их число пропорционально концентрации компоненты водного раствора [2]. Таким образом, общее число молекул компоненты будет пропорционально следующему выражению:

С Q-a С, где коэффициент ос зависит от величины L Н. Положительное значение коэффициента а означает, что рассматриваемая компонента высаживается из водного рас твора в виде твердофазного соединения на дно водоема. Отрицательным значениям а будет соответствовать растворение некоторого минерала в результате нарушения термо гидродинамического режима течения водного потока.

Верховье р. Чикой обозначим индексом 1, приток - индексом 2, а нижнее устье р. Чикой - индексом 3. Тогда речная система р. Чикой - р. Киран можно описать уравнением:

река 1 + приток 2 = река 3.

Баланс веществ для водной системы, где в результате смешения генетически разных вод формируется новый состав воды, будет выглядеть как

С vQ₁-ocC^+C₂Q₁-

-PC 2=С ^Q^-aC у '

Аналогично коэффициенту а коэффициент р учитывает высаживание или растворение минерализующей компоненты для бокового притока. Поскольку взаимодействием всех компонент мы пренебрегаем, то коэффициенты а и р будут одинаковы для всех минерализующих компонент. Для учета сезонной зависимости коэффициентов а и Р воспользуемся результатами режимных наблюдений, представленных в табл. 2, находим зима: ос = 23.7, Р = 3.3 весна: а = 102, Д = -13 лето: а = -383, р - 7,6 осень: а = 377,Д = -22.

Для коэффициента а мы выписали три значащих цифры, а для Р - две цифры. Доверительный интервал не приводим. Это связано с тем, что приведенным выше значениям коэффициентов а и р удовлетворяют 80 % данных, приведенных в табл. 2. Для остальных данных можно только предположить, что они либо измерялись с большой ошибкой, либо их измерение производилось в другом месте водного потока.

Заключение

Введенные коэффициенты а и р зависят от характеристик русловой сети, и теоретическое выявление этой связи пока не представляется возможным. Коэффициен- ты учитывают способность минерализующих субстанций оседать на дно или взмучиваться. По знаку коэффициента а в сезонные периоды можно заключить, что осенью, зимой и весной минералы осаждаются, а летом они взмучиваются, что приводит к дополнительному загрязнению водоема. Для коэффициента Р видно, что его величина периодически меняет знак. Зимой и летом минералы в притоке осаждаются, а весной и осенью взмучиваются. По абсолютной величине коэффициентов а и Р можно судить об интенсивности процессов осаждения и взмучивания.

Из анализа табл. I следует, например, что зимой и осенью для притока величина Bh равна 4,6 *4.7. Весной уменьшается почти в два раза, до значения 2.7. Однако летом В h принимает максимальное зна чение 8.6.

Впервые предложена двумерная модель течения рек, позволяющая связать характеристики русла (ширина, глубина) с измеряемыми величинами (средняя скорость, расходы). Установлено, что по измерению концентраций загрязняющих веществ можно судить о процессах осаждения и взмучивания.