Морфометрический подход в оценке величины площади поверхности таллома многоклеточной водоросли Callithamnion corymbosum (J. E. Smith) Lyngb

Введение. В физиологических и экологических исследованиях часто проводятся расчеты поточных характеристик по отношению к физиологически активной поверхности растений (Мокроносов, 1981; Хайлов, 1984; Хайлов и др., 1992). Для водных многоклеточных водорослей такой поверхностью является вся поверхность таллома. По отношению к сложно-разветвленным слоевищам водорослей используется поэтапная технология определения площади их поверхности (Фирсов, 1984; Хайлов, Фирсов, 1985; Хайлов и др., 1992; Празукин, 2015), и, в соответствии с особенностями морфологии того или иного объекта, существуют определенные нюансы её исполнения.

Цель настоящей работы: на примере многоклеточной водоросли CaUithamnion corymbosum (J. Е. Smith) Lyngb. продемонстрировать морфометрический подход в оценке величины площади поверхности слоевища и оценить роль каждого класса морфологических структур С. corymbosum в формировании её ассимиляционной поверхности.

Материал и методика. В апреле-мае 2015 г., в период наших исследований, на преимущественно затененных участках горизонтальных и вертикальных стенках скал открытых участков Севастопольского прибрежья до глубин 30-40 см С. corymbosum формировала сплошные заросли (растительный покров).

Для подробной морфометрии слоевищ С. corymbosum отбирали отдельные кустики растений (рис. 1а), формируемые одним вертикальным «побегом» (Ко, рис. 1 б). В структуре вертикального побега отчетливо выделяется главная ось (Коо), которая является основой для всех последующих порядков осевых структур (Koi - Кою , рис. 1 б - г) и ветви разного уровня организации (Ki - Кд, рис. 1 в, г). «Ветвь» рассматривается нами как сложноразветвленный элемент слоевища (иерархически организованный ансамбль осевых структур), обладающий собственной морфофункциональной структурой, закономерно меняющейся во времени (Фирсов, 1984; Хайлов и др., 1992; Празукин 2008, 2015). В таком случае, ветвь первого порядка (К_ь рис. 1 в, д) - это ось первого порядка (Koi) со всеми осевыми структурами последующих порядков ветвления (К02 - Кою), аналогично, ветвь второго порядка (К2, рис. 1 в) - это ось второго порядка (К02) со всеми осевыми структурами последующих порядков ветвления (Коз - Кою)- Ветвь четвертого порядка (Кд) состоит из осевых структур Код - Кою, ветвящихся дихотомически (рис. 1 г).

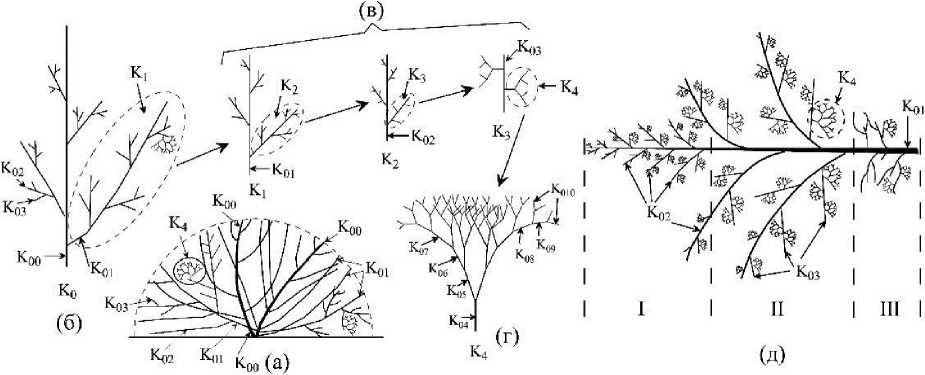
Рис. 1. Различные уровни организации Callithamnion corymbosum; а -куст, образованный двумя вертикальными «побегами; схема осевого аппарата вертикального «побега» (б) и ветвей первого - третьего (в) и четвертого (г) порядков; д - схема осевой структуры ветви первого порядка Коо, К₀1 - Кою - осевые структуры нулевого («ствол»), первого -десятого порядка ветвления; К_о - вертикальный «побег»; К! - К₄ - ветви первого - четвертого порядка; I - III - морфологические отделы ветви первого порядка выделяемые вдоль оси К₀]

Особенностью структуры слоевища С. corymbosum является то, что основная масса растения и его фотосинтезирующая поверхность (S) создается за счет относительно небольшого числа крупных ветвей первого порядка (Ki, рис. 1 в, д ), отрастающих от самой нижней части оси Коо. Это позволило нам сосредоточить внимание на морфометрии крупных ветвей первого порядка. Ветви первого порядка расчленяли на ось Koi и ветви второго порядка (К2). Последние, в соответствии с длиной оси К02, делили на три условные группы: «мелкие» (0.2 - 0.6 см), «средние» (>0.6 - 0.8 см) и «крупные» (1.3 — 1.8 см). Крупные ветви К2 были, как правило, немногочисленными и располагались в среднем отделе ветви Ki (рис. 1 д). Далее, из каждой размерной группы ветвей отбирали по три-пять К2 и каждую ветвь расчленяли на ось К02 и ветви К3. Подробно морфометрировали ветви четвертого порядка (К4, рис. 1 г).

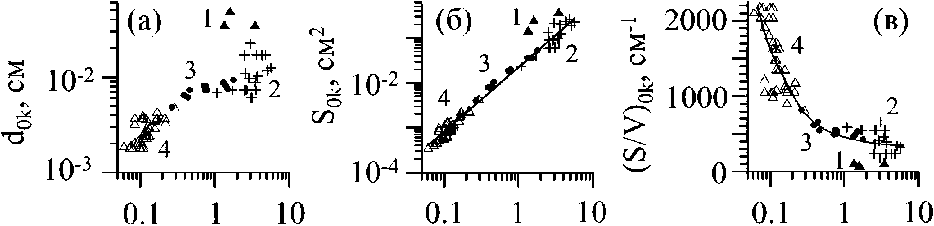
4k’ СМ

Рис. 2 . Связь между диаметром (d_Ok), площадью поверхности (8_0к) и удельной поверхностью ((S/V)ok) осевых структур разного порядка ветвления Callithamnion corymbosum, - с одной стороны, и, соответственно, с их длиной (7_0к), с другой Осевые структуры нулевого, «ствол» (1), первого (2), второго (3) и третьего (4) порядка ветвления

Во всех случаях с помощью бинокулярной лупы МБС-1 измеряли длину (/ок) и диаметр (dok) осевых структур нулевого, первого - десятого порядка ветвления. Величина диаметра осевых структур рассчитывалась как средняя по результатам нескольких измерений на разных участках структур. Подсчитывали общую численность структур последующего порядка (nok+i) на осевых структурах предыдущего (0k).

Геометрический объем (Vok, см3) и геометрическую поверхность (Sok, см2) осевых структур рассчитывали по формулам, подходящим для аппроксимации их геометрических фигур: цилиндра, усеченного конуса, полусферы и их комбинаций (Выгодский, 1965).

Результаты и обсуждение. Вначале рассмотрим структурную организацию слоевища С. corymbosum, что позволит на следующем этапе рассмотрения представить алгоритм расчета площади поверхности этого вида водорослей.

Слоевище С. corymbosum в своей структуре сочетает моноподиальное (осевые структуры нулевого - четвертого порядка, рис. 1 а, б) и дихотомическое (ветви четвертого порядка, рис. 1 г) типы ветвления. Для осевых структур каждого порядка ветвления характерны собственные диапазоны варьирования значений параметров: длины (Zok), диаметра (dok), объёма (Уок), площади поверхности (Sok) и удельной поверхности (S/V)ok (рис. 2, 3). В ряду порядков, от первого до четвертого, длина, диаметр, площадь поверхности и объем осевых структур быстро снижаются, а удельная поверхность повышается. Особенность такой динамики lok и dok состоит в том, что в ряду порядков длина уменьшается в 130 раз быстрее диаметра. Для цистозиры косматой (Cystoseira crinita (Desf.) Вогу) этот показатель равен четырем (Хайлов и др., 1992), а для бриопсиса перистого (Bryopsis plumosa (Huds.) Ar.) - трем (Празукин, 2007). У С. corymbosum моноподиальное ветвление ограничено четырьмя порядками ветвления, у цистозир - четырьмя, реже - пятью-шестью, у бриопсиса перистого - пятью. Можно предположить, что существуют минимальные размеры структур (lok, dok) и их соотношения, при которых дальнейшее моноподиальное ветвление становится невозможным, и в случае с С. corymbosum осевые структуры пятого и последующих порядков ветвления ветвятся дихотомически (рис. 1 г).

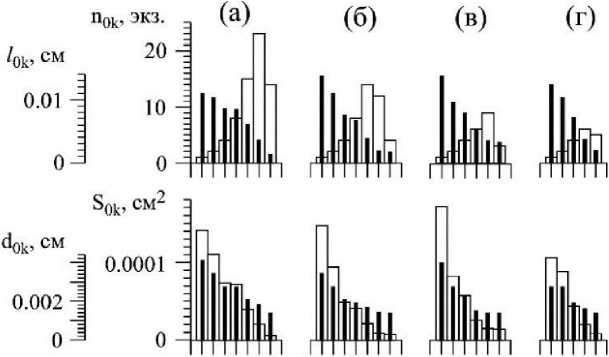
Возможно, и при дихотомическом ветвлении существует ограничение в количестве последовательных генераций осевых структур. В структуре ветвей четвертого порядка С. corymbosum их насчитывается 4-6 (рис. 3). При дихотомическом ветвлении численность осевых структур в каждой последующей генерации удваивается, но это правило нарушается на завершающем акте ветвления, и в этом случае численность структур снижается (рис. 3).

В ряду порядков структур (Ко4 - Кою) происходит одновременно как уменьшение значений длины (/ок), так и диаметра (dok) без существенного изменения их пропорций (рис. 3). Наблюдаемое снижение значений /ок и dok нельзя рассматривать как прямое следствие дихотомического ветвления. Так, например, у церамиума шиповидного (Ceramium echionotum J. Ag.) при аналогичном типе ветвления у осевых структур уменьшение значений длины и диаметра обнаруживается только на завершающих этапах ветвления (Хайлов и др., 1992).

EVOk, см3 VOk, см3

РЮ"7

0.5*10-7

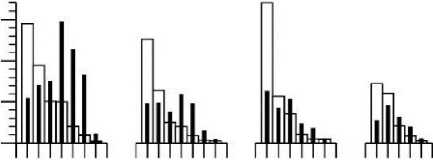
SSOk, см2 (S/V)Ok, см"1 0.0004 2000 4 0.0002 0^    0

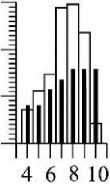
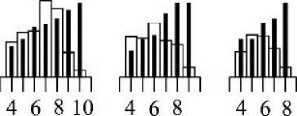
Рис.

порядок ветвления

3 . Средние значения индивидуальных параметров и значения кумулятивных характеристик осевых структур разных порядков ветвления у четырех ветвей четвертого порядка (К4) Callithamnion corymbosum, взятых с ветвей второго порядка разного размерного диапазона: «крупные» (а), «средние» (б, в), «мелкие» (г) (см. табл. 1)

VOk- объём осевой структуры; nok, ZVok, Z^ok, - соответственно, численность, суммарный объём и суммарная площадь поверхности осевых структур каждого порядка ветвления. Обозначение остальных параметров те же, что на рис. 2

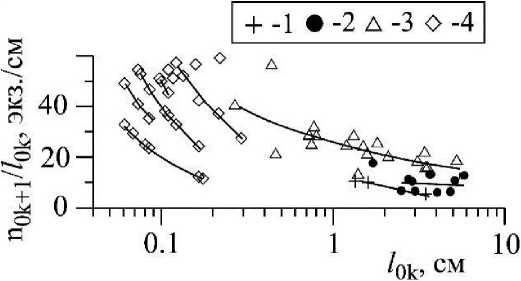
Рис. 4 . Плотность размещения осевых структур последующего порядка на осевых структурах предыдущего порядка (n_Ok+i//ok) как функция длины осевых структур (Z_ok) Callithamnion corymbosum

1 - 4 - плотность размещения осевых структур первого - четвертого порядка ветвления на структурах предыдущего порядка

Суммарная поверхность (ZSok) и суммарный объём (ZVok) структур в ряду порядков ветвления ветви четвертого порядка С. corymbosum изменяются по одновершинной зависимости, а их соотношение (S/V)ok увеличивается (рис. 3). По отношению ко всей ветви К4 величина площади поверхности укладывается в диапазоне от 0.00116 до 0.0018 см², а удельная поверхность - от 1600 до 1800 см"¹ (табл. 1, 2).

В табл. 1 и 2 представлены средние значения параметров осевых структур и ветвей первого и четвертого порядка ветвления, что позволяет проследить последовательность «сборки» ветвей, начиная с третьего и заканчивая первым порядком ветвления.

Общий объем (Усл) и общая поверхность (8СЛ) слоевища складываются, соответственно, из объема и поверхности ствола (оси нулевого порядка, Voo, Soo) и объема и поверхности всех ветвей первого порядка (ZVb ZSi):

Усл = Уоо + ЕУь

SM = Soo + ZSb

Таблица!

Средние значения параметров осевых структур и ветвей ________________1-4 порядков (К! - К4)

Ветви первого порядка (К,)     ’

Ветви второго порядка (К2)

Ветви третьего порядка (Кз)

К,

Si, см2

Soi, см2

Размерные группы ветвей К2 по Lq2 , СМ

Ветви второго порядка (К2)

s2, см2

S02, см2

СМ

поз/ ^02, экз./см

s3, см2

8оз, см2

СМ

noV /оз экз./см

s4, см2

П

ES, см2

6,271

246 Е-3

Мелкие (0.2-0.6)

62

373 Е-2

602 Е-4

83 Е-4

0,39

393 Е-1

338 Е-5

70 Е-5

97 Е-3

412 Е-1

7 Е-4

Средние (>0.6-0.8)

4

76 Е-2

1893 Е-4

168 Е-4

0,76

289 Е-1

784 Е-5

86 Е-5

И Е-2

542 Е-1

12 Е-4

Крупные (1.3-1.8)

5

154 Е-2

3070 Е-4

222 Е-4

1,58

216 Е-1

833 Е-5

113 Е-5

15 Е-2

263 Е-1

18 Е-4

V,,

Voi, см3

Lq2 , СМ

п

XV,

v2.

Vq2>

СМ

Поз/ /о2

v3.

V03,

СМ

П04/ /оз

v4.

5189 Е-6

846 Е-6

Мелкие (0.2-0.6)

62

28 Е-4

451Е-7

148Е-7

0,39

393 Е-1

198Е-8

447Е-9

97 Е-3

412 Е-1

38 Е-8

Средние (>0.6-0.8)

4

5 Е-4

133Е-6

299Е-7

0,76

289 Е-1

470 Е-8

553Е-9

И Е-2

542 Е-1

69 Е-8

Крупные! 1.3 1.8)

5

10 Е-4

202Е-6

250Е-7

1,58

216 Е-1

518Е-8

827Е-9

15 Е-2

263 Е-1

И Е-7

В свою очередь, объем (Vi) и поверхность (Si) ветвей первого порядка складываются, соответственно, из объема и поверхности оси первого порядка (V01, S01) и объема, и поверхности всех ветвей второго порядка (ZV2, £S2):

Vi = Voi+ZV2,(1)

Si = S01 + ZS2, (2)

Последовательно раскрывая уравнения (1) и (2), получаем:

V 1 - Vol + n₀2 (V₀2 + Поз (Vo3 + n₄JV₄)), (3)

Si = Soi + П02 (So2 + Поз (8оз + n₄ S₄)). (4)

По отношению к ветвям второго порядка можно записать:

V₂ = V02 + Поз (V₀3 + n₄ V₄), (5)

§2 ⁼ §02 + Поз (8оз + n₄ S₄), (6)

а по отношению к ветвям третьего порядка:

Уз = У₀з + п₄у₄, (7)

S3 = So3 + n4S4. (8)

Таблица2

Средние значения удельной поверхности (S/У) осевых структур и ветвей первого - четвертого порядка

Осевые структуры и ветви первого порядка		Размерные группы ветвей К2 ПО L02 , см	Осевые структуры второго - третьего порядка		Ветви второго - четвертого порядка
(S/V)oi, см"1	(S/V)b см"1		(S/V)02, см"1	(8/У)оз, см"1	(S/V)2, см"1	(S/V)3, см"1	(S/V)4, см"1
291	1209	Мелкие (0.2-0.6)	562	1560	1334	1709	1752
		Средние (>0.6-0.8)	562	1561	1421	1669	1683
		Крупные (1.3-1.8)	891	1365	1519	1608	1654

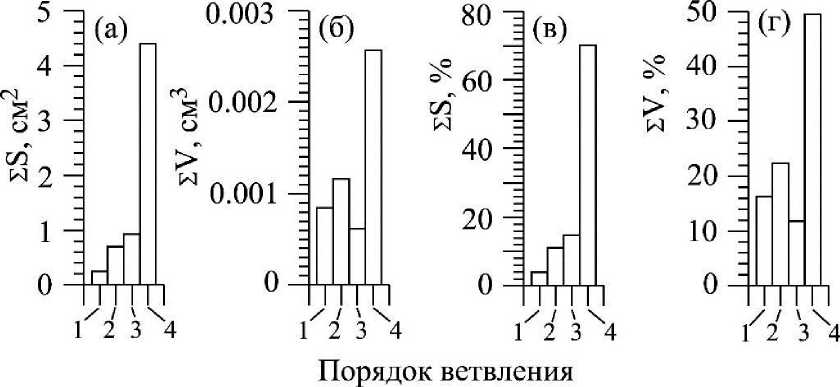
Рис. 5 . Суммарная площадь поверхности (а) и суммарный объем (б) осевых структур (1 - 3 - K_Oi - К₀₃) и ветвей четвертого порядка (4 - К₄) в структуре ветви первого порядка (КО Callithamnion corymbosum и вклад названных структур в общую поверхность (в) и объем (г) ветви К,

По сути, мы имеем дело с процессом формирования ветвей и, в целом, всего слоевища. Его можно представить как результат иерархического «обрастания»: на растущей осевой структуре нулевого порядка («стволе») появляются дочерние оси-эпифиты (Koi), а на них, в свою очередь, - дочерние оси (Ко2) и т. д. (рис. 1). В этом случае, при расчетах общей поверхности ветви или всего слоевища становится важной такая характеристика как плотность размещения осевых структур последующего порядка на осевых структурах предыдущего (nOk+i//ok). Как следует из рис. 4, эта характеристика является функцией длины осевых структур предыдущего порядка ветвления (/ок), и названная связь хорошо обнаруживается по отношению к осевым структурам третьего и четвертого порядка ветвления. Плотность размещения К04 на структурах третьего порядка во многом зависит и от индивидуальных размеров структур второго порядка (/02, табл. 1), что проявляется в широком диапазоне варьирования значений (11.4 -59.2 экз. см'1) этого показателя (noV/оз, рис. 4). В целом, в ряду порядков от нулевого до третьего плотность размещения осевых структур увеличивается с 5.5 экз. см"1 на осевых структурах нулевого порядка до 59.2 экз. см"1 на осевых структурах третьего порядка.

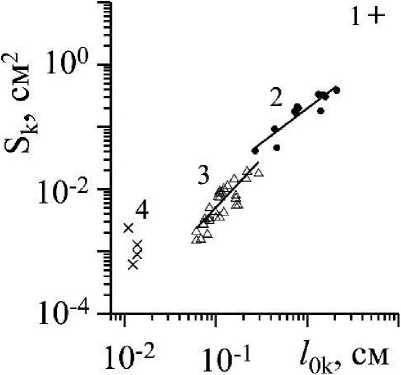
Рис. 6 . Зависимость площади поверхности (Sk) ветвей первого -четвертого порядка ветвления от длины осевых структур соответствующего порядка ветвления (ZOk) 1 - 4 - ветви первого - четвертого порядка ветвления

В композиционной структуре ветви первого порядка (Ki, рис. 1 д) С. corymbosum выделяются две группы морфологических объектов: собственно осевые структуры первого - третьего порядка ветвления (Koi - Коз, рис. 1 д ) и ветви четвертого порядка (Кд, рис. 1 д). Вторые, по сравнению с первыми, отличаются относительно небольшими значениями индивидуальных характеристик (/оь Vok, Sok), но, в то же время, они превосходят осевые структуры первого - третьего порядка по величине удельной поверхности (S/V)ok, рис. 2 в, табл. 2) и по численности их в структуре ветви Ki, а значит и по суммарной площади поверхности (£S). За счет ветвей четвертого порядка формируется 70% площади поверхности ветви первого порядка (рис. 5). Учитывая и тот факт, что ветви четвертого порядка обладают наиболее активной фотосинтезирующей поверхностью (Празукин, 2015), по сравнению со структурами предыдущих порядков ветвления (Koi - КОД то можно заключить, что эти структуры выполняют основную роль в формировании общего потока карбонатного углерода ветви Ki и всего растения в целом. Аналогичная картина наблюдается и в структуре ветвей Ki В. plumosa. Поверхность ветви Ki этого вида на 72.6 % складывается из поверхностей «коротких» (мелкоразмерных) осевых структур, доля которых в общей массе ветви составляет 53 % (Празукин, 2007).

Теперь обратимся непосредственно к вопросу об определении величины площади поверхности слоевища С. Corymbosum и его морфологических структур.

По результатам измерений морфологических параметров ветвей К2 и Кз (табл. 1), взятых с одной и той же ветви Ki С. Corymbosum, была проведена численная «сборка» вышеназванных объектов, рассчитана их площадь поверхности (Sk, см²) и построены зависимости (Sk = f(/ok), рис. 6), описываемые следующими уравнениями регрессии:

LogS2 = -0.702 + 1.105 log/02 (R2 = 0.84, n = 12), (9)

LogS3 = -0.728 + 1.564 log/03 (R2 = 0.68, n = 35). (10)

Таким образом, площади поверхностей ветвей второго и третьего порядка можно легко определить, рассчитав её по регрессионным уравнениям: (9) и (10). Для определения площади поверхности ветвей первого порядка потребуются дополнительные расчеты, учитывающие особенности её структуры (рис. 1 д).

Согласно уравнению (2) площадь поверхности ветви первого порядка (Si) равна сумме площадей поверхностей оси первого порядка (Soi) и всех ветвей второго порядка (£82). Для установления величины Soi достаточно измерить длину (Zoi) и диаметр (doi) осевой структуры и рассчитать Soi по формуле усеченного конуса (Выгодский, 1965). Для расчета величины £S2 вначале необходимо по уравнению (9) рассчитать величину 82 каждой ветви К2, а затем полученные значения суммировать.

Определение величины площади поверхности ветви К2 можно осуществлять и в результате ее индивидуальной «сборки». 82 - как сумма площадей поверхностей оси второго порядка (S02) и всех ветвей третьего порядка (£83): S2 = S02 + £83. В таком случае, площадь поверхности каждой ветви третьего порядка (S3) рассчитывается по уравнению (10).

Заключение. Можно сказать, что для установления величины площади поверхности ветвей первого - третьего порядка С. corymbosum достаточно измерить такие легко определяемые морфологические параметры, как длину (Zok) и диаметр (dok) осевых структур соответствующего порядка ветвления и воспользоваться регрессионными уравнениями (9) и (10).

Празукин А.В. Морфометрический подход в оценке величины площади поверхности таллома многоклеточной водоросли CaUithamnion corymbosum (J. Е. Smith) Lyngb / А.В. Празукин // Вести. ТвГУ. Сер.: Биология и экология. 2016. № 4. С. 195-205.