Может ли радиальное число вихревых мод управлять орбитальным угловым моментом?
Автор: Воляр Александр Владимирович, Абрамочкин Евгений Григорьевич, Брецько Михаил Владимирович, Акимова Яна Евгеньевна, Егоров Юрий Александрович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 6 т.46, 2022 года.
Бесплатный доступ
В общем случае стандартный пучок Лагерра-Гаусса, состояние которого задаётся двумя квантовыми числами - радиальным числом n и азимутальным числом l (или топологическим зарядом вихря, переносимым пучком Лагерра-Гаусса), является неустойчивым относительно слабых возмущений. Это нетрудно заметить, если разложить комплексную амплитуду пучка Лагерра-Гаусса по модам Эрмита-Гаусса, общее число которых равно N = 2 n + l +1. Изменяя амплитуды и фазы коэффициентов разложения с помощью возмущающих параметров, можно существенно трансформировать первоначальную радиально симметричную структуру пучка Лагерра-Гаусса. Мы назвали композицию мод Эрмита-Гаусса, зависящую от двух возмущающих параметров (амплитудный параметр e, фазовый параметр q), структурированным пучком Лагерра-Гаусса. При изменении этих параметров орбитальный угловой момент структурированного пучка Лагерра-Гаусса меняется в интервале (-l, l), а полный топологический заряд - в интервале (-2 n - l, 2 n + l). При n = 0 изменение орбитального углового момента в интервале (-l, l) является плавным, а с ростом n поведение орбитального углового момента становится всё более осциллирующим. Число минимумов (максимумов) осцилляций равно радиальному числу в интервале q = (0, p) и q = (p, 2p), а их амплитуда нелинейно зависит от разности l - n , за исключением точки q = p, где сЛГ-пучок становится вырожденным. Если же l = 0, то орбитальный угловой момент = 0 и в структуре структурированного пучка Лагерра-Гаусса возникает либо симметричный массив вихрей с противоположными знаками топологического заряда, либо узор краевых дислокаций, число которых равно радиальному числу n . Также мы обнаружили, что, несмотря на быстрые осцилляции орбитального углового момента, абсолютное значение полного топологического заряда структурированного пучка не изменяется при вариации как амплитудного e, так и фазового параметра q, но зависит исключительно от исходного состояния ( n , l) пучка Лагерра-Гаусса и равно модулю (2 n + l).
Структурная устойчивость, топологический заряд, орбитальный угловой момент, спектр вихрей
Короткий адрес: https://sciup.org/140296231
IDR: 140296231 | DOI: 10.18287/2412-6179-CO-1169
Текст научной статьи Может ли радиальное число вихревых мод управлять орбитальным угловым моментом?
Для единичного ЛГ-пучка ответ на вопрос в заголовке статьи вполне ожидаем: конечно, нет. Для композиции ЛГ-пучков с одинаковым ТЗ ответ тот же: конечно, нет. Как правило, орбитальный угловой момент (ОУМ) единичных осесимметричных вихревых пучков однозначно связан с их азимутальными числами £, иначе говоря, с их топологическими зарядами (ТЗ) [1]. Если комплексные амплитуды Т параксиальных вихревых пучков нормированы, то ОУМ суперпозиции таких пучков (мод) также ассоциируется с их ТЗ [2] £z = Z££ |c£|2, где c£ - амплитуды вихревых мод, Z££ |c£|2=1. Более сложная ситуация возникает для несимметричных пучков, а также комбинаций вихревых мод. Принято считать [3], что ОУМ лазерных пучков можно разделить на внутренний и внешний. Внутренний ОУМ определяется геликоидальным волновым фронтом (или непосредственно его фазовыми сингулярностями, оптическими вихрями), тогда как внешний ОУМ задаётся сдвигом пучков относительно общей оси, деформацией формы поперечного сечения или астигматизмом. Внутренний и внешний ОУМ можно измерить в эксперименте, используя метод моментов интенсивности [4]. Более того, можно достичь больших значений ОУМ простой деформа- цией безвихревых лазерных пучков [5]. Управление параметрами массива внеосевых вихревых и безвихревых пучков позволяет либо многократно увеличивать ОУМ [6], либо полностью его компенсировать [7]. Тем не менее, зависимость ОУМ от радиального числа не была замечена. Однако деформация вихревых пучков неявно приводит к возникновению такой зависимости [8]. Более того, зависимость от радиального числа начинает существенно сказываться на ОУМ в симметричных ЛГ-пучках, подверженных комплексному сдвигу [9]. Таким образом, в ряде статей был обнаружен эффект зависимости ОУМ от радиального числа за счёт либо деформации вихревых пучков, либо их несимметричных сдвигов, что можно отнести к внешним проявлениям ОУМ. В настоящей работе мы рассмотрим проблему влияния радиального числа на ТЗ вихревых мод и ОУМ в структурированных осесимметричных пучках [10,11]. Недавно была опубликована статья [12], в которой авторы теоретически рассматривают ОУМ в композиции пучков Эрмита–Гаусса (ЭГ) с различными амплитудами. Однако ими не был затронут вопрос влияния радиального и азимутального числа результирующего структурированного вихревого пучка на ОУМ при изменении амплитуд и фаз ЭГ-мод.
Целью нашей статьи является исследование ОУМ и общего ТЗ структурированных ЛГ-пучков, в составе которых каждая ЭГ-мода испытывает двухпараметрическое гармоническое возбуждение амплитуды и начальной фазы.
-
1. Двухпараметрическое возбуждение ЭГ-мод в структурированном ЛГ-пучке
Использование многих степеней свободы структурированных пучков предполагает ввод полезной информации в каждую его независимую моду [10]. Однако изменение амплитуд и фаз этих мод неизбежно приводит к нарушению структурной устойчивости пучка в целом и резкому изменения ОУМ. Поэтому возбуждение собственных мод можно рассматривать как внутреннее возмущение структурированных пучка в отличие от внешнего возмущения , источником которого являются регулярные и случайные возмущения внешней среды. Отклик структурированного пучка на внутренние возмущения зависит от свойств вихревых мод в его составе и способов детектирования введенной информации. Как мы покажем ниже, ОУМ всего структурированного пучка может существенно отличаться от ОУМ мод пучка при возбуждении безвихревых ЭГ-мод. Более того, радиальное число структурированного пучка может существенно изменять как ТЗ каждой моды, так и ОУМ пучка в целом.
-
1.1. Комплексная амплитуда структурированного ЛГ-пучка
В работе [13] мы показали, что фильтрация ЭГ-мод в составе ЛГ-пучков может существенно изме- нять свойства структурированного пучка в целом. Там же было показано, насколько чувствительна такая волновая конструкция к небольшим изменениям амплитудного параметра. В этом подпараграфе мы рассмотрим, как изменяется вихревая структура пучка при возбуждении кратными фазами каждой ЭГ-моды и как вариация амплитудного параметра разделяет структурированный пучок на два структурно устойчивых семейства.
Структурированный ЛГ-пучок (сЛГ) можно представить в базисе ЭГ-мод в виде
(-1) n sLG„ t (r, e, 6) = — x n-tv ’ ’ ' 22n+31/2 n !
2 n+t x Y (2i)k pn+<-k-n-k) (0)ek (e, 6№n+,-k,k (r) k=0
где r = (x,y), Pk(n+1 -k, n-k)(•) - многочлен Якоби и ek (e, 6) - возмущающие коэффициенты. В невозмущенном случае, ek (0,0) =1, сЛГ-пучок превращается в стандартную ЛГ-моду [14]. Мы хотим узнать, как изменится вихревая структура ЛГ-пучка для случая e k (e, 6) = 1 + e eik 6, (2)
т.е. когда к каждой ЭГ-моде добавлено амплитудное возмущение e и фазовое возмущение, кратное 6 .
Суперпозицию мод (1) с учетом возмущения (2) можно существенно упростить (см. Приложение А) и записать при I > 0 как sLGn ,t (r, e, 6) = LGn л (r) +
■ n-t + I ( 2 n + < )« ( ,
+ e — ----HLG„ „+f I x+y
2 n +< n ! n ’ n + t I 72
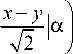
где
“= 2 ( 6-2 Л ) .
Фактически комплексная амплитуда (3) показывает, что возбужденное состояние сЛГ-пучка представляет собой сумму двух стандартных мод: ЛГ-моды и гибридной Эрмит–Лагерр–Гауссовой (ЭЛГ) моды, структурой которой управляют амплитудный e и фазовый 6 параметры. Из формулы (3) следует, что вариация амплитудного параметра e позволяет разделить возмущенный ЛГ-пучок на два структурно устойчивых семейства: 1) для e< 1 сЛГ-пучок, содержащий две стандартных ЛГ- и ЭЛГ-моды; 2) для e ^ 1 сЛГ-пучок превращается в стандартную ЭЛГ-моду с одним управляющим параметром 6 . Рис. 1 иллюстрирует картины интенсивности и фазы этих двух семейств.
В многообразии структурных преобразований на рис. 1 привлекают внимание характерные картины для трех значений фазового параметра 6: л /2, л, 3л /2 и обоих значений амплитудного параметра. Так, в случае e = 1 и 6 = л / 2 возникает суперпозиция ЛГ- и ЭГ-мод (т.к. HLGn, n+z(r | л /2) = in HGn+л n(r) [14]) с одинаковыми весами, а в случае е = 1 и 9 = 3л /2 картина интенсивности и фазы поворачивается на угол л /2, в то время как при е =100 возникают почти чистые состояния ЭГ-мод, ориентированные под углами л /4 и 3л /4. В случае 9 = л при е = 1 формируется вырожденное состояние ЛГ-пучка, состоящее из суммы ЛГ-мод с противоположными знаками ТЗ, а при е =100 формируется ЛГ-пучок с противоположным знаком ТЗ.
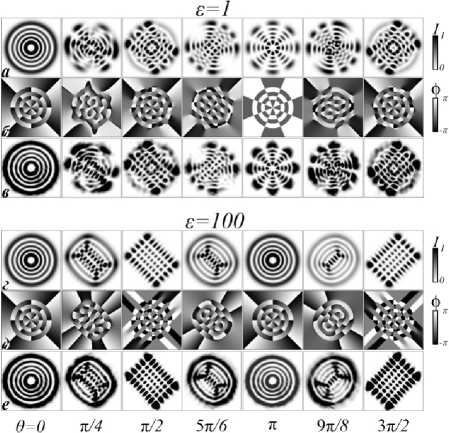
Рис. 1. Теоретические (а, г) и экспериментальные (в, е) картины интенсивности и фазы (б, д) сЛГ-пучка для двух амплитудных параметров е = 1 и е = 100 и некоторых значений фазового параметра 9
Важно отметить, что каждый сЛГ-пучок остаётся структурно устойчивым при распространении при любых значениях параметров возмущения, поскольку каждая ЭГ-мода в разложении (1) получает одно и то же значение фазы Гуи, равное Г=(2 n + £ +1)arctg( z / z о ), где z 0 – длина Рэлея.
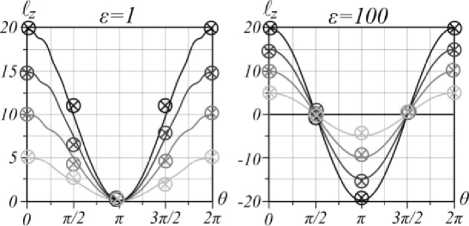
Рис. 2. ОУМ & ( 9 ) как функция фазового параметра 9 в двух семействах сЛГ-пучков, е = 1 и е = 100, при радиальном числе n = 0 и азимутальных числах 1= 5, 10, 15, 20. Непрерывные кривые - теория, перекрещенные кружочки – эксперимент
-
1.2. Быстрые осцилляции ОУМ
Для ответа на вопрос, поставленный в заголовке статьи, необходимо разложить комплексную амплитуду сЛГ-пучка (3) по базису ЛГ-мод. Как показано в Приложении Б :
2 n +'
sLG n ,' ( r , е , 9 ) - У c k LGmin,2 n +'- 2 k ( r ), (4)
k -0
i n + k e i ( 2 n +' ) 6/2
Ck - 8» k + (-1)™1П е------------2max min!x k n ’ k ’ 2n+' n! (5)
xsinn-k (29) cosn+'-k (29)Pk(n-k•n+'-k)(cos 9), где min = min (2n +£ - k, k), max = max (2n +£ - k, k) и 8n, k - символ Кронекера. Радиальное v = min и азимутальное ц = 2n + £ -2k числа связаны между собой полным числом мод 2v + ц +1=2n + £ +1 в сЛГ-пучке. Именно это приводит к перепутыванию радиального числа и ТЗ-мод. Такое перепутывание не изменяет свойства самих собственных ЛГ-мод, но радикально изменяет свойства всего сЛГ-пучка в целом. Коллективное влияние перепутывания следует искать в суммарных характеристиках сЛГ-пучков, к которым относятся ОУМ и общий ТЗ.
Амплитуды ЛГ-мод и их ТЗ в (4) позволяют записать выражение для ОУМ, предварительно отнорми-ровав ЛГ-моды:
2n+'2
'z - £ (2n +' - 2k) |Ck| У |ck|, k-0
где ск - C k -| |LG min,2 n +'- 2k ( r )|| и нормировочные коэффициенты ЛГ-мод хорошо известны (см. (B5)).
Для сЛГ-пучка это общее выражение сводится к более простому виду (см. Приложение Б ):
1 + 2 е cos ( 72 (2 n + ' ) 9 ) cos ' ( 2 9 ) P”^ (cos 9 ) +е 2 cos 9
' z - ' 1 + 2 е cos ( 2 (2 n + ' ) 9 ) cos ' ( 2 9 ) p0^ (cos 9 ) +е 2 . ( 7)
Как простое следствие, отсюда легко получить асимптотическую формулу для ОУМ: £ z ^ ^cos 9 при е » 1. Кроме того, если радиальное число равно нулю ( n =0), то ОУМ запишется в виде
1 + 2 е cos (| ' 9 ) cos ' ( 2 9 ) + е 2 cos 9 z - 1 + 2 е cos ( 72 ' 9 ) cos ' ( 2 9 ) + е 2 .
На рис. 2 показаны кривые £ z ( 9 ), построенные по формуле (8), для случаев е = 1 и е » 1. При е = 1 ОУМ обращается в ноль в одной точке 9 = л . Стоит только амплитудному параметру превысить единицу е > 1, как особенность в нуле расщепляется на две точки, где ОУМ обращается в ноль в окрестности точки 9 = л . По мере увеличения амплитудного параметра точки нулей стремятся к 9 = л /2 и 9 = 3 л /2, в то время как ОУМ стремится к максимальному ОУМ с противоположным знаком ТЗ.
Когда радиальное число становится ненулевым, n ^ 0, то на графиках ОУМ возникают осцилляции, характер которых показан на рис. 3. Чем больше разность между радиальным n и азимутальным £ числами, тем больше частота осцилляций.
Но для наших исследований важным является проблема связи числа нулей ОУМ и полного ТЗ структурированного ЛГ-пучка, которую мы рассмотрим в следующем подпараграфе. Здесь же мы отметим, что положение нулей ОУМ удобно исследовать, приравняв нулю числитель выражения (7):
1 + 2 е cos ( 2 (2 n + / ) 9 } cos 2 ( 2 9 ) x x Pn0^ (cos 9 ) + е 2cos 9- 0.
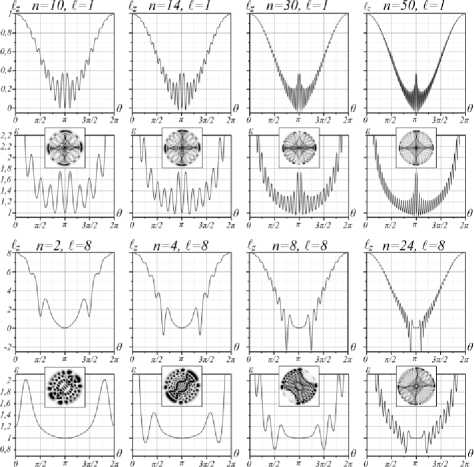
Рис. 3. Зависимость ОУМ £ z ( 9 ) от фазового параметра 9 (первая и третья строки сверху) и положение нулей ОУМ на плоскости параметров ( е 9 ) (вторая и четвертая строки) для двух случаев исходного ТЗ £=1 и £= 8. На вставках приведены картины интенсивности для 9 = 3 л /4
Осцилляции положения нулей ОУМ на плоскости параметров ( е , 9 ) показаны на рис. 3. Заметим, что нули ОУМ появляются в широкой области амплитудных параметров е . Но нас будет интересовать в основном возникновение нулей ОУМ при критическом условии е = 1, когда амплитуды ЛГ- и ЭЛГ-мод одинаковы и ярко проявляются свойства сЛГ-пучков.
Интересная ситуация возникает в случае нулевого азимутального числа (I = 0) сЛГ-пучка при произвольном значении радиального числа n. ОУМ пучка обращается в ноль, но оптические вихри в структуре пучка не исчезают. Как видно из рис. 4а,в, пары вихрей с противоположными по знаку ТЗ, но равными «весами» группируются в симметричные топологические диполи. Спектры ЛГ-мод (4) становятся симметричными относительно состояния k = n. Такая картина наблюдается для всех 9^л/2, л, 3л/2. В точках 9 = л /2, 3л /2 оптические вихри с противоположными знаками ТЗ аннигилируют, образуя узор краевых дислокаций, как показано на рис. 4б,г. В точке 9 = л замкнутые фигурные дислокации вырождаются в семейство концентрических колец, соответствующих стандартной ЛГ-моде с n =4 (или n = 8), так что в спектре ЛГ-мод присутствует только одна линия с k =4 (или k = 8). Напомним, что радиальное число ЛГ-моды изменяется с индексом k как v = min(2n + I -k, k), а азимутальное число – в соответствии с выражением ц = 2n + I -2k.
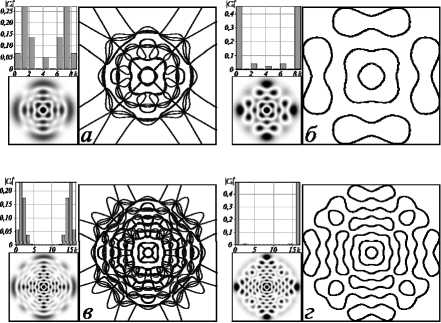
Рис. 4. Линии равной фазы для состояний (n, £: (a) (4,0), 9 = л /4, (б) (4,0), 9 = л /2; (в) (8,0) 9 = л /4, (г) (8,0), 9 = л /2. На выносках представлены картины интенсивностей и спектры ЛГ-мод |c k |2 для соответствующих состояний сЛГ-пучка, е = 1
-
1.3. Топологические инварианты сЛГ-пучков и их измерение
Быстрые осцилляции ОУМ являются коллективным откликом множества ЛГ-мод в сЛГ-пучке на перемешивание в них радиальных и азимутальных чисел. При этом свойства собственных ЛГ-мод не изменяются, но радикально изменяют свойства структурированного пучка таким образом, что ОУМ может многократно менять знак при вариации фазового параметра. Возникает вопрос, какие физические характеристики сЛГ-пучка остаются неизменными на фоне быстрых осцилляций ОУМ? Как мы видели в предыдущем подпараграфе, обращение в ноль ОУМ при е = 1 и 9 = л сопровождается перестройкой картины фазы в виде сетки краевых дислокаций. Поэтому нас заинтересовал вопрос, какое перераспределение фаз ЛГ-мод возникает в случае дополнительных нулей ОУМ?
На рис. 5 a,в представлены картины интенсивности и теоретические линии равной фазы (рис. 5 б,г ) сЛГ-пучка в случае обращения в ноль ОУМ в точке (рис. 5 а, б ) е =1, 9 = 0,9 л в состоянии n = 1, I=2 и для пучка ( в, г ) в состоянии n = 8, I=4 в точке е = 1, 9^ 0,86 л . Заметим их отличие от состояния пучка с нулевым ОУМ при 9^л (см. рис. 1), где формируется вырожденная ЛГ-мода из Ь радиальных краевых дислокаций и n кольцевых дислокаций. В нашем же случае (рис. 5 б, г ) возникает система топологических диполей [15, 16] (пары вихрей с противоположными знаками ТЗ, покрывающих все поперечное сечение пучка). Даже небольшое изменение параметров пучка приводит к резкому изменению картин интенсивности и фазы.
Тем не менее, внутри этого процесса имеются скрытые инварианты, которые остаются неизменны- ми при быстрых осцилляциях ОУМ. В этом подпараграфе мы займёмся поиском таких инвариантов.
(е- 1,9-3,46рад, п-4, £=2)
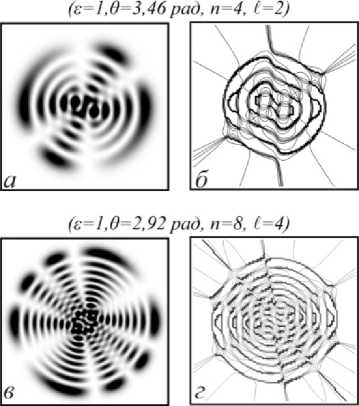
(в-1,9-2,92 рад, п-8, 1=4)
Рис. 5. Картины интенсивности (а, в) и контуры равной фазы (б, г) сЛГ-пучка в состояниях (а, б) n = 4,£= 2 в точке
£ = 1 9 = 0,9 л и (в, г) n = 8, £ = 4 в точке е = 1, 9 = 0,86 л
PC
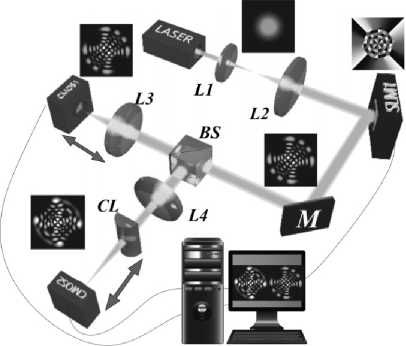
Рис. 6. Схема экспериментальной установки: LASER–He-Ne-лазер, SLM – пространственный модулятор света, L1-L4 – сферические линзы, CL – цилиндрическая линза, BS – делительный кубик (1:1±0,03); CMOS1, CMOS2 – фотодетекторы, M – зеркало, PC – компьютер
Прежде всего, необходимо выяснить, как можно измерить в эксперименте быстрые осцилляции ОУМ? Чтобы обнаружить осцилляции ОУМ, мы использовали метод моментов интенсивности, и процесс измерения спектра ЛГ-мод на экспериментальной установке, схема которой показана на рис. 6.
Метод моментов интенсивности, используемый для измерения спектра ЛГ-мод, подробно рассмотрен в статье [13]. Основной проблемой при измерении осцилляций ОУМ является ошибка измерений. Нам удалось снизить относительную ошибку измерений до 2,7% за счёт использования улучшенного типа пространственного модулятора света (Thorlabs EXULUS-4K1/M) и фотодетекторов типа Michrome
20. В качестве источника света использовался He-Ne-лазер типа Thorlabs HNL100RB с длиной волны X = 0,633 мкм.
В качестве примера на рис. 7 представлены 3D-спектры ЛГ-мод для е = 1 с 9 = л /2 и 9 = л при n = £ = 4 и n = £ = 8 соответственно. Выбранные состояния пучка соответствуют случаю, когда энергия в основном сосредоточена в двух модах: ЛГ- и гибридной ЭЛГ-моде. Если ЛГ-моде на рис. 7 а,в для 9 = л /2 соответствует только один яркий всплеск энергии, то энергия гибридной ЭЛГ-моды распределена среди 12 ЛГ-мод для пучка sLG 4,4 (рис. 7 а ), а для sLG 8,8 уже присутствует 24 ЛГ-моды, что следует из выражения (4). В случае 9 = л (рис. 7 б,г ) наблюдается только две стандартные ЛГ-моды с противоположными знаками ТЗ. Здесь важно подчеркнуть, что в формирование вторичных ЛГ-мод дают основной вклад кратные периодические возбуждения ЭГ-мод (см. выражения (1) и (2)). Причем радиальные n и азимутальные £ числа сЛГ-пучка перепутываются между собой при его формировании. По нашему мнению, такой совокупный вклад возбуждённых ЛГ-мод и приводит к сложному виду спектров на рис. 7 даже для простых состояний пучка.
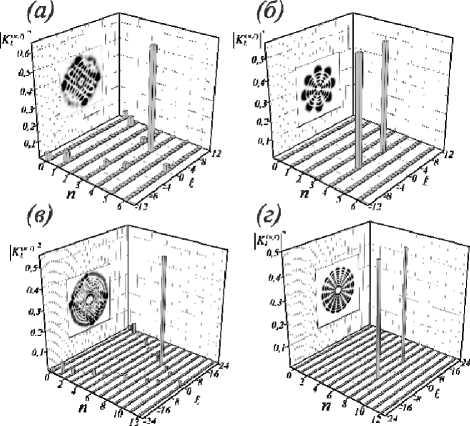
Рис. 7. Измеренные 3D-спектры ЛГ-мод | K kn ^ |2 структурированных мод: (a, б) sLG 4,4 и (в, г) sLG 8,8 c (a, в) 9 = л / 2 и (б, г) 9 = л при £ = 1
При измерении характера быстрых осцилляций ОУМ нужно учитывать систематические ошибки, вносимые оптическими узлами, и случайные ошибки измерений. Систематические ошибки следует ожидать из-за недостаточно высокой разрешающей способности SLM-модулятора и фотодетекторов. Случайные ошибки сопровождают процесс измерений.
Для оценки предельных условий разрешающей способности модулятора пучка и фотодетектора достаточно сравнить предельные возможности этих устройств с минимальными расстояниями между ну- лями интенсивности сЛГ-пучка. В нашей экспериментальной установке использовался SLM EXULUS-4K1/M модулятор с диагональю рабочего элемента 20,21 мм и размером зерна 3,7 мкм, а также фотодетекторы CMOS Michrome 20 с диагональю рабочего элемента 15,86 мм и размером одного зерна 2,4 мкм. С другой стороны, расстояние между соседними нулями вдоль оси x ЭГ-моды можно найти из асимптотического представления четного многочлена Эрмита [17]: Н2n(x/w) ~ cos(V4n"+Tx/w), где w — радиус перетяжки пучка, n > 50. Тогда расстояние между соседними нулями интенсивности будет Ax = wл/^4n +1. Отсюда видно, что даже для ЭГ-пучка с n > 100 расстояние между соседними нулями интенсивности будет значительно больше, чем размер зерна, как на модуляторе, так и на фотодетекторе, при условии, что пучок полностью покрывает минимальную площадь рабочих элементов. Заметим, что в наших экспериментах нет сЛГ-пучков с максимальным числом n = 100.
Тем не менее, метод измерения ОУМ накладывает некоторые ограничения на экспериментальное определение положения нулей максимумов и минимумов функции £ z ( 9 ). Рассмотрим этот вопрос подробнее. На рис. 8 представлены графики зависимости ОУМ £ z от фазового параметра 9 .
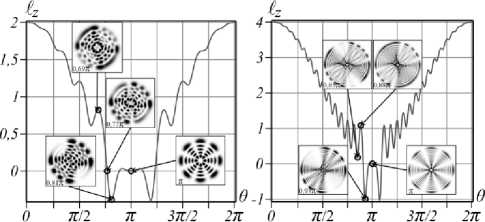
Рис. 8. Осцилляции ОУМ /z (9) и их измерение в сЛГ-пучке в состояниях (а) n = 4, /= 2 и (б) n = 14, /= 4. На выносках картины интенсивности в критических точках: (a) для максимума 9= 0,69л для нулей 9= 0,77ли 9= л минимума 9= 0,81л; (б) максимума 9= 0,88л минимумов 9= 0,85л и 9= 0,93л нуля 9= л
Картины интенсивности, расположенные на выносках рис. 8, соответствуют состояниям пучка в максимумах, минимумах и нулях ОУМ. Именно анализ этих распределений интенсивности позволяет определить амплитуды ЛГ-мод в составе сЛГ-пучка. Измерение амплитуд ЛГ-мод позволяет определить ОУМ по формуле (6). Важно отметить, что ошибка измерений ОУМ пропорциональна сумме произведений азимутального числа ± (2 n + £ -2 k ) на среднюю погрешность измерения квадрата амплитуды ЛГ-моды (2,7%) в данной точке кривой £ z ( 9 ). Анализ состояния сЛГ с n = 4, £ = 2 на рис. 8 а показывает, что положения максимума ( 9 = 0,69 л ), первого нуля ( 9 = 0,77 л ) и минимума ( 9 = 0,81 л ) ОУМ вполне различимы. Однако измерения ОУМ в минимуме
( 9 = 0,81 л ) и во втором нуле ОУМ ( 9 = л ) лежат внутри ошибки измерений. В то же время ошибка измерений позволяет хорошо различать все особые точки ОУМ структурированного пучка в состоянии n = 14, £ = 4 на рис. 8 б . По-видимому, чем больше разность радиального и азимутального чисел, тем с большей точностью можно воспроизвести зависимость £ z ( 9 ) в эксперименте. Однако по мере увеличения азимутального числа £ амплитуды осцилляций уменьшаются (см. третью и четвёртую строки на рис. 3) и в эксперименте эти осцилляции неразличимы за исключением узкой области вблизи 9 = л .
В то же время на фоне таких быстрых осцилляций ОУМ можно найти физическую характеристику, которая остаётся неизменной в широком интервале изменения параметров е и 9 . Действительно, это следует из условия постоянства числа мод, 2 n + £ + 1, в сЛГ-пучке. Обратим внимание на полный ТЗ структурированного пучка. Согласно недавней работе [18] общий ТЗ структурированного пучка, состоящего из ЛГ-мод, задаётся азимутальным числом ЛГ-моды с большим модулем амплитуды. Если же модули амплитуд мод с противоположными знаками ТЗ одинаковы, то сравниваются амплитуды с предыдущими азимутальными числами. Вырожденное состояние структурированного пучка возникает при условии равенства амплитуд всех мод с положительными и отрицательными знаками азимутальных чисел. Теперь мы должны ответить на два вопроса: 1) следует ли изменение знака общего ТЗ структурированного пучка за его ОУМ? 2) насколько точно мы можем различить в эксперименте изменение знака общего ТЗ?
Ответ на первый вопрос даёт рис. 9, на котором изображены контуры квадратов амплитуд | ск ( 9 ) |2 с максимальными ТЗ и противоположными знаками. Смена знаков ТЗ происходит при 9 = л /2 и 9 = 3 л /2 для любых состояний ( n , £) сЛГ-пучка, какие-либо осцилляции амплитуд отсутствуют. Чтобы ответить на второй вопрос, необходимо определить минимальный интервал фазовых параметров A9 , на краях которого можно надёжно разделить в эксперименте квадраты амплитуд ЛГ-мод с положительными и отрицательными ТЗ, то есть определить условия, при которых разность измеренных квадратов амплитуд | ck ( 9 )|2 будет превышать ошибку эксперимента. Заметим, что амплитудам | ck ( 9 ) |2 с максимальными ТЗ соответствуют индексы k =0 и k =2 n +£, при этом радиальное число равно нулю min(2 n +£ - k , k )=0. Топологически нейтральное состояние наступает при k = (2 n + £)/2, в эксперименте оно наблюдается только для чётных £. Примеры надёжного измерения интервалов A9 , на краях которых различие квадратов амплитуд превышает ошибку измерений, приведены на рис. 9.
Так, для sLG15,5 получается интервал фазовых параметров 9е (0,44л; 0,56л), где в эксперименте знак ТЗ остаётся неопределённым; для состояния sLG15,15 получается интервал 9е (0,45л; 0,53л). На выносках к рисункам приведены картины интенсивности на краях соответствующих интервалов фазовых параметров. В остальной области фазовых параметров общий ТЗ структурированного пучка не изменяется, принимая одинаковые значения с точностью до знака. Таким образом, модуль общего ТЗ структурированного ЛГ-пучка является инвариантом процесса двухпараметрического возбуждения мод сЛГ-пучка.
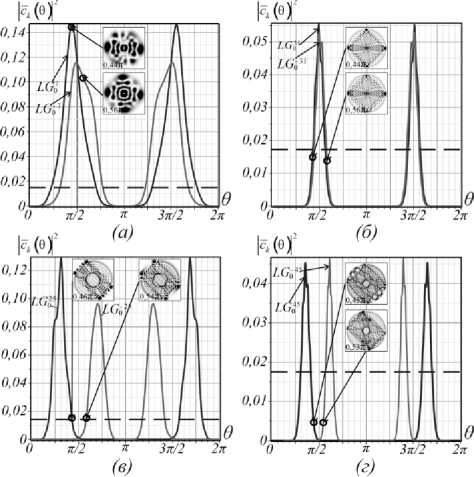
Рис. 9. Контуры квадратов амплитуд ЛГ-мод | c k ( 6 ) |2 с максимальными положительными и отрицательными ТЗ для начальных состояний сЛГ-пучков: (а) n = 3, £= 1;
(б) n = 15, £= 1; (в) n = 5, £= 15 и (г) n = 15, £= 15.
На вставках приведены картины интенсивности сЛГ-пучка на границах области надежного измерения ЛГ-мод с противоположными знаками ТЗ: (а) 9 = 0,44 л и 9 = 0,56 л ;
(б) 9 = 0,44 л и 9 = 0,56 л ; (в) 9 = 0,46 л и 9 = 0,54 л ;
(г) 9 = 0,45 л и 9 = 0,53 л
Выводы
Рассмотрено двухпараметрическое возбуждение ЭГ-мод в структурированных ЛГ-пучках, при котором амплитудный параметр е меняет амплитуды массива ЭГ-мод, а фазовый параметр 6 вносит кратную начальную фазу в каждую ЭГ-моду. Теоретически и экспериментально обнаружено, что в общем случае сЛГ-пучок при кратных гармонических возбуждениях ЭГ-мод является суммой двух сингулярных пучков – стандартного ЛГ-пучка и гибридного ЭЛГ-пучка. При больших значениях амплитудного параметра структурированный ЛГ-пучок превращается в гибридный ЭЛГ-пучок, ось которого повёрнута на угол л /4. Вариация фазового параметра 6 вызывает быстрые осцилляции ОУМ при отличном от нуля радиальном числе n, которые сглаживаются при n = 0 или при больших значениях амплитудного параметра е. Быстрые осцилляции ОУМ связаны с перепутыванием ра- диальных и азимутальных чисел в сЛГ-пучке. Такое перепутывание не меняет свойств собственных ЛГ-мод, но радикально изменяет свойства сЛГ-пучка. Мы нашли, что структурированный ЛГ-пучок с радиальным числом n и азимутальным числом I содержит 2n + I + 1 мод в интервале азимутальных чисел (-(2n +I), 2n + €). Также на основе компьютерного моделирования было обнаружено, что ТЗ структурированного пучка может принимать значения 2n + I или (- (2n + I) при изменении фазового параметра 6. Если амплитудный параметр меньше или равен единице, а радиальное число равно нулю, то ТЗ структурированного пучка остается неизменным в интервале 6 от 0 до 2л, за исключением единственной точки 6 = л. Если же амплитудный параметр очень большой (е>>1), то ТЗ меняет знак в точках 6 = л/2 и 6 = 3л/2. В общем случае ненулевых значений радиальных чисел общий ТЗ структурированного ЛГ-пучка остаётся неизменным за исключением узких интервалов параметров 6, где знак ТЗ остаётся неопределённым.
Работа выполнена при поддержке грантов РФФИ в части «Двухпараметрическое возбуждение ЭГ-мод в структурированном ЛГ-пучке» (проект № 20-3790066), в части «Комплексная амплитуда структурированного ЛГ-пучка» (проект № 20-37-90068), в части «Быстрые осцилляции ОУМ» (проект № 19-2901233), а также гранта Государственного Совета Республики Крым в части «Топологические инварианты сЛГ-пучков и их измерение».
Список литературы Может ли радиальное число вихревых мод управлять орбитальным угловым моментом?
- Allen L, Beijersbergen MW, Spreew RJC, Woerdman JP. Orbital angular momentum and the transformation of Gauss-Laguerre modes. Phys Rev A 1992; 45(11): 81858189. DOI: 10.1103/PhysRevA.45.8185.
- Berry MV. Paraxial beams of spinning light. Proc SPIE 1998; 3487: 6-11. DOI: 10.1117/12.317704.
- Van Enk SJ, Nienhuis G. Commutation rules and eigenvalues of spin and orbital angular momentum of radiation fields. J Mod Opt 1994; 41(5): 963-977. DOI: 10.1080/09500349414550911.
- Fadeyeva TA, Rubass AF, Aleksandrov RV, Volyar AV. Does the optical angular momentum change smoothly in fractional-charged vortex beams? J Opt Soc Am B 2014; 31(4): 798-805. DOI: 10.1364/JOSAB.31.000798.
- Kotlyar VV, Kovalev AA. Vortex-free laser beam with an orbital angular momentum. Computer Optics 2017; 41(4): 573-576. DOI: 10.18287/2412-6179-2017-41-4-573-576.
- Izdebskaya YV, Shvedov VG, Volyar AV. Symmetric array of off-axis singular beams: spiral beams and their critical points. J Opt Soc Am A 2008; 25(1): 171-181. DOI: 10.1364/JOSAA.25.000171.
- Aksenov VP, Dudorov VV, Filimonov GA, Kolosov VV, Venediktov VYu. Vortex beams with zero orbital angular momentum and non-zero topological charge. Opt Laser Technol 2018; 104: 159-163. DOI: 10.1016/j.optlastec.2018.02.022.
- Kovalev AA, Kotlyar VV, Porfirev AP. Asymmetric Laguerre-Gaussian beams. Phys Rev A 2016; 93(6): 063858. DOI: 10.1103/PhysRevA.93.063858.
- Najafi-Nezhad F, Azizian-Kalandaragh Y, Akhlaghi EA, Amiri P, Porfirev A, Khonina S, Najarbashi G. Superposition of shifted Laguerre-Gaussian beams. Optik 2021; 227: 165147. DOI: 10.1016/j.ijleo.2020.165147.
- Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photonics 2021; 15: 253-262. DOI: 10.1038/s41566-021-00780-4.
- Shen Y, Yang X, Naidoo D, Fu X, Forbes A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica 2020; 7(7): 820-831. DOI: 10.1364/OPTICA.382994.
- Kotlyar VV, Kovalev AA. Orbital angular momentum of paraxial propagation-invariant laser beams. J Opt Soc Am A 2022; 39(6): 1061-1065. DOI: 10.1364/JOSAA.457660.
- Volyar A, Abramochkin E, Egorov Yu, Bretsko M, Akimova Y. Fine structure of perturbed Laguerre-Gaussian beams: Hermite-Gaussian mode spectra and topological charge. Appl Opt 2020; 59(25): 7680-7687. DOI: 10.1364/AO.396557.
- Abramochkin EG, Volostnikov VG. The modern optics of the Gaussian beams [In Russian]. Мoscow: "Fizmatlit" Publisher; 2010. ISBN: 978-5-9221-1216-1.
- Berry MV. Wave dislocations in non-paraxial Gaussian beams. J Mod Opt 1998; 45(9): 1845-1858. DOI: 10.1080/09500349808231706.
- Volyar AV, Shvedov VG, Fadeeva TA. The structure of a nonparaxial Gaussian beam near the focus: II. Optical vortices. Optics and Spectroscopy 2001; 90: 93-100. DOI: 10.1134/1.1343551.
- Szego G. Orthogonal polynomials [In Russian]. Moscow: "Fizmatgiz" Publisher; 1962.
- Kotlyar VV, Kovalev AA, Volyar AV. Topological charge of a linear combination of optical vortices: topological competition. Opt Express 2020; 28(6): 8266-8281. DOI: 10.1364/OE.386401.


