MPI-реализация численного решения системы уравнений, описывающих модель длинных джозефсоновских переходов

Интерес к математическому моделированию физических процессов в стеках длинных джозефсо-новских переходов (ДДП) обусловлен, помимо необходимости получения фундаментальных знаний о свойствах слоистых джозефсоновских структур, открывающейся перспективой практических приложений в сверхпроводящей электронике. В частности, недавно было обнаружено достаточно мощное когерентное электромагнитное излучение в терагерцовой области частот из данной системы [1]. Экспериментальные и теоретические исследования терагерцового излучения из стека внутренних джозефсоновских переходов в слоистых сверхпроводниках интенсивно проводятся в настоящее время в Японии, США и Германии.

Расчет физических характеристик ДДП сводится к численному решению систем уравнений синус-Гордона в широком диапазоне параметров, что требует существенных затрат компьютерного времени. В этой связи важную роль приобретает развитие методов компьютерного моделирования, включая разработку параллельных алгоритмов для повышения эффективности численного исследования.

В настоящей работе рассматривается обобщенная модель, учитывающая индуктивную и емкостную связь между ДП. Система связанных ДДП предполагается состоящей из ^ + 1 сверхпроводящих слоев c промежуточными диэлектрическими слоями (рис. 1).

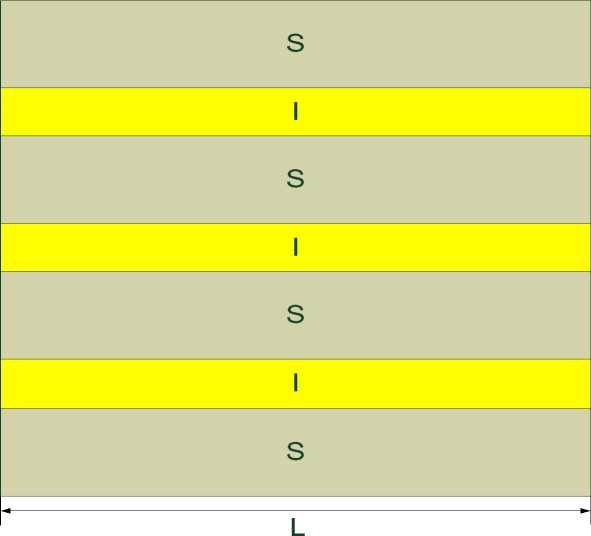
Рис. 1. Структура стека джозефсоновских переходов длины L. S – сверхпроводящие слои, I – диэлектрические слои

1. Постановка задачи

Система уравнений, определяющая фазовую динамику системы ДДП с учетом емкостной и ин

дуктивной связи между контактами, имеет следующий вид [2]:

{ 9V i

9t

Эф,

V = DcVi + scVi+! + scVi-i at

N   _r-1 ^J^              ^Эф1    ,

= L n=1 ⁽^^n "^ ^- 5^^пф₁^- p — + I

где £ - матрица индуктивной связи:

/ 1 s 0  -       s\

£ = ,/° ^S 1 S V...

\ S       -  0 S 1 /

Здесь ф г (х, t) и V_;(%, t) - соответственно разность фаз и напряжение в 1 м ДП стека (I = 1,..., N), Р = ^V₀/(d_Ij_c^>) - параметр диссипации, S - параметр индуктивной связи, который принимает значения в интервале 0 < |S| <  0.5 . D_c - эффективная электрическая толщина ДП, нормированная на толщину диэлектрического слоя. s_c - параметр емкостной связи, I - внешний ток. Все величины в системе (1) переведены в безразмерные [2].

Граничные условия:

VZ(0, t) = Vl(L, t) = ^^^(0,^) = ^^^^ = 0.                            (3)

Ол        Ол

• 2.    Численный метод

Для численного решения системы (1–3) вводится равномерная дискретная сетка по пространственной координате х с шагом Ах и по координате времени t с шагом At. Для аппроксимации производных по пространственной координате используются стандартные трехточечные конечноразностные формулы. Полученная система обыкновенных дифференциальных уравнений относительно значений разностей фаз ф ^ и напряжений V ; в узлах дискретной сетки по х решается численно с использованием метода Рунге-Кутта (РК) четвертого порядка. Вычисления проводились при Ах = 0.05. Шаг по t был выбран At = Ах/5 на основе проведенных методических расчетов, чтобы обеспечить выполнение условия Куранта и устойчивость вычислительной схемы.

Одной из главных физических характеристик системы ДДП является вольт-амперная характеристика (ВАХ), отражающая динамику изменения усредненного по контактам и времени значения напряжения при изменении внешнего тока. Для вычисления ВАХ на каждом шаге по времени вычисляется интеграл

v (t) = (1/L) J0LVz(x,t) dx                                   (4)

с использованием формулы Симпсона. Далее вычисляется интеграл

(vz) = 1/ (Tmax - Tmin) Jrm" V (t)dt

1 min на основе метода прямоугольников и, наконец, напряжение усредняется по числу контактов

(V) = Sf=i(vz).

Расчеты начинаются при I = I_mZn = 0.01 c нулевыми начальными условиями. Значение тока увеличивается до I_max = 1.1 с шагом 0.005 и затем уменьшается до нуля. При необходимости в выделенных интервалах расчет проводится с более мелким шагом по току. В процессе расчета к току добавляется шум порядка SI = ±10^-8. Для каждого значения I расчет проводится до T_max = 200. Далее полученные значения напряжения и разности фаз используются в качестве начальных условий при расчете для следующего значения I.

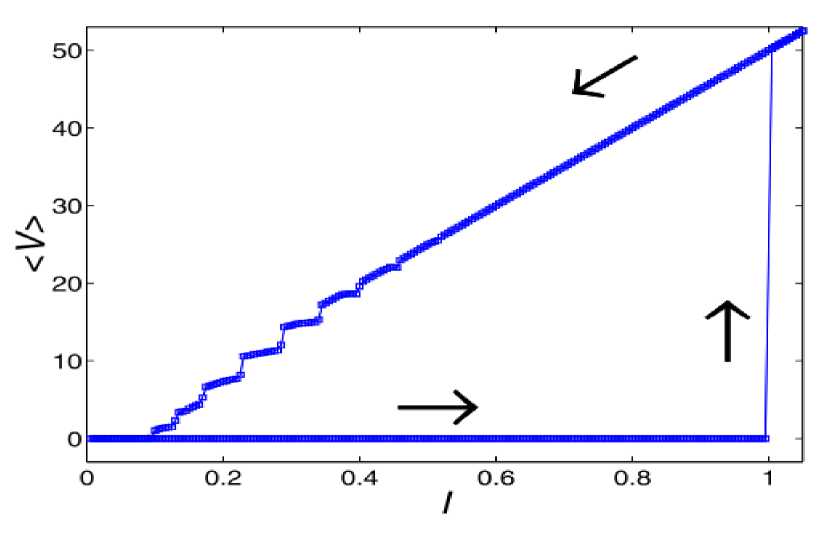
Рис. 2. ВАХ для случая N = 5 , L = 10 , Р = 0.1 , 5 = -0.05 , D_c = 1.1 , s_c = 0.05

В качестве примера на рис. 2 представлена типичная структура ВАХ. Показан случай N = 5, L = 10, Р = 0.1,5 = -0.05, D_c = 1.1, s_c = 0.05. Начальное нулевое напряжение при определенном значении тока I скачкообразно возрастает, далее происходит плавный рост при увеличении I до I_max.

При уменьшении / от /_тах до нуля кривая V (/) имеет иную форму и содержит так называемые ступеньки Шапиро [2].

Описанная здесь вычислительная схема и соответствующий компьютерный код успешно прошли апробацию путем сравнения полученных на его основе результатов c расчетами в рамках другого подхода, представленного в [4].

• 3.    Параллельная реализация на основе технологии MPI

Разработанный параллельный алгоритм основан на распределении вычислений по узлам дискретной сетки по координате х вдоль длины контакта. Параллельная реализация выполнена с использованием технологии MPI. Каждому из задействованных в расчете параллельных MPI-процессов назначается своя порция узлов дискретной сетки по координате. Каждый процесс в назначенных ему узлах в параллельном режиме вычисляет рекурсивно коэффициенты Рунге-Кутта и затем решения V и ф_г системы уравнений. Такой расчет на каждом шаге по времени производится для каждого контакта с номером l. В ходе вычислений соседние процессы обмениваются необходимыми им для дальнейших расчетов значениями коэффициентов Рунге-Кутта и решений V ,

z

в граничных узлах назначенных этим процессам порций узлов дискретной сетки. При расчете ВАХ сначала каждым процессом вычисляются частичные суммы в соответствии с формулой Симпсона, далее производится сборка в 0й процесс, где и осуществляются окончательные вычисления ВАХ и запись в файлы. При необходимости аналогичным образом осуществляются расчеты других физических характеристик стека ДДП [3].

Таблица 1. Зависимость времени счета (в минутах) от числа P параллельных MPI-процессов при расчете с разными значениями N и L

N	L	P = 1	P = 2	P = 4	P = 6	P = 8	P = 10	P = 12	P = 14
10	5	33,37	17,93	10,11	9	7,03	6,18	6,19	8,4
10	10	67,08	34,86	18,31	13,37	11,06	9,65	9,67	11,74
5	10	26,2	13,4	7,6	5,9	5,06	4,4	4,3	5,3

Расчеты выполнены на многопроцессорном кластере ЦИВК Многофункционального центра обработки и хранения информации (ЛИТ ОИЯИ, Дубна). Расчеты выполнены при Р = 0.1,5 = -0.05, D_c = 1.1, s_c = 0.05. В Таблице 1 и на Рис. 3 представлены результаты расчетов для стека с 5 и 10 джозефсоновскими переходами и длиной контакта 5 и 10 при Р = 0,1. При этом ток увеличивается от минимального значения / min = 0.01 до /_max = 1.1, затем уменьшается до нуля. Шаг по координате Д% = 0.05. Временной домен составляет 100 с параметром дискретизации At = Д%/5. Шаг по току равен 0,005. Из таблицы видно, что наименьшее время счета достигается на 10 процессах и далее меняется незначительно. Отметим, что рассмотренная вычислительная схема требует значительных объемов межпроцессорного взаимодействия, что ограничивает эффективность распараллеливания. Тем не менее, параллельная реализация обеспечивает ускорение до 7 раз по сравнению с однопроце-сорным режимом расчета.

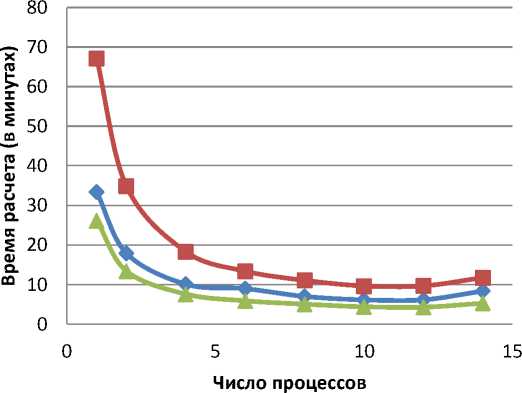
Рис. 3. Время расчета (в минутах) ВАХ в зависимости от числа параллельных MPI-процессов для разных значений N и L. Расчеты выполнены на многопроцессорном кластере ЦИВК Многофункционального центра обработки и хранения информации (ЛИТ ОИЯИ, Дубна).

Расчеты выполнены при Р = 0.1 , S = -0.05 , D_c = 1.1 , s_c = 0.05

Заключение

В работе представлен параллельный алгоритм для численного исследования модели длинных джозефсоновских переходов с учетом емкостной и индуктивной связей, описываемой системой уравнений (1–3). Проведенные методические вычисления на многопроцессорном кластере ЦИВК Лаборатории информационных технологий подтверждают эффективность разработанного подхода и его реализации на основе технологии MPI. Показано, что расчет в параллельном режиме обеспечивает в типовых расчетах ускорение до 7 раз по сравнению с работой в однопроцессорном режиме. Для дальнейшего уменьшения времени счета необходима существенная модификация вычислительной схемы решения системы (1–3).

Работа выполнена при поддержке РФФИ, грант 15-29-01217.