Multi-dimensional Range Query on Outsourced Database with Strong Privacy Guarantee

Published Online October 2017 in MECS DOI: 10.5815/ijcnis.2017.10.02

The cloud computing paradigm has been recognized as an important solution for drastically reducing data storage and processing costs. Recent years have witnessed an increasing trend toward outsourcing data storage to cloud computing platforms such as Amazon EC2 [1], Google App Engine [2], and Microsoft Azure [3]. Companies and service providers in various fields, such as law enforcement, finance, and healthcare, are exploring solutions for outsourcing data. Outsourcing data enables clients to reduce not only infrastructure costs but also human costs.

Despite its advantages, data outsourcing has raised critical concerns over data privacy. It not only deprives clients of direct control over their data but also allows the server to gain direct access to the client data. Thus, information leakage can occur on the server side in various ways. The first threat is from corrupt employees who are able to access and reveal sensitive client information. Even if a cloud computing platform implements sufficiently robust policies against such privacy violations, it may be vulnerable to external malicious attacks. A successful cyberattack may lead to full exposure of client data. This threat is becoming increasingly apparent owing to the popularity of cyberattacks as services. Such threats are realistic, and a number of data breaches have been reported recently. Therefore, outsourcing plaintext datasets is strongly discouraged.

Data encryption is considered as the solution to the issue of data confidentiality. However, the context of data outsourcing introduces new challenges to managing encrypted data. The most critical issue is to preserve data usability in the encrypted dataset. This challenge has attracted considerable attention from both industry and academia in recent years. Searchable encryption techniques have been proposed to enable users to efficiently use their remote encrypted data without retrieving the entire data or exposing sensitive data to the data server. However, most existing methods focus on the problem of keyword matching and are inherently unsuitable for handling certain types of complex queries, such as multi-dimensional range queries, where the plaintexts are multi-numerical attributes.

In this paper, we study the problem of supporting an important class of complex search operations, namely multi-dimensional range queries. Multi-dimensional range queries are required for a wide range of practical applications, including network traffic log analysis, longterm health monitoring, and banking audits. There are essentially three broad categories of solutions: special data structure for range query evaluation, bucketization-based scheme, and order-preserving encryption-based techniques. However, these techniques fail to provide rigorous privacy protection owing to their statistical patterns, access patterns, or query leakage. Moreover, nearly all existing solutions support only static data (i.e., data that have been uploaded to the server only once) and previously known queries. To address the abovementioned issues, this paper proposes a three-party architecture and investigates different protocols that support multi-dimensional range queries over encrypted remote data while rigorously guaranteeing privacy. We examine both static and dynamic cases in which data records can be appended to the existing data set. In addition, solutions for both fixed and unknown sets of queried attributes are studied.

The remainder of this paper is organized as follows. Section II reviews related studies on secure multidimensional range queries. Section III formulates the problem statement. Section IV describes our system model as well as the requirements for the designed protocols. Section V discusses the solution for the fulldomain query in which the set of queried attributes is fixed and unchanged for all queries. This type of query is similar to most existing techniques for multi-dimensional range queries. Section VI presents solutions for a generalized version where the set of queried attributes can dynamically vary for different queries. The naive approach to this problem is to apply multiple single range queries. However, this approach leads to singledimensional privacy leakage. In the proposed protocol, we leverage the concept of secure set intersection to resolve this issue. Section VII discusses practical considerations for the system implementation. Finally, Section VIII concludes the paper.

• II.    Related Works

This section reviews existing approaches toward to problem of secure multi-dimensional range query as well as oblivious RAM – a useful cryptographic technique we utilize to design the solutions.

• A.    Secure Range Query

There are essentially three general approaches for tackling multi-dimensional range queries on encrypted data: special data structure for range query evaluation, bucketization-based scheme, and order-preserving encryption-based techniques.

Special data structure . Boneh et al. [4] proposed a general public-key approach to support comparison, subset, and range queries on encrypted data by using hidden vector encryption, whose search complexity is O(mT), where m and T are the number of attributes and number of discrete values for each attribute, respectively. Moreover, the ciphertext size is relatively large owing to the use of composite-order bilinear map groups [5], which make it infeasible in many applications.

Shi et al. [6] proposed a scheme that supports a conjunction of range queries over multiple attributes (i.e., multi-dimensional range queries). The idea is to encrypt each data record as a point in multi-dimensional space. The query processing is equivalent to testing whether a point falls inside a hyper-rectangle for every data record. The authors used a segment tree data structure to represent the ranges for each dimension. Anonymous identity-based encryption is applied at each node of the tree with a different key. For a certain query, the client needs to reveal the keys corresponding to each range on each dimension. Hence, all the attributes on the range will be revealed after successful decryption at the server. Subsequently, different tree-based approaches have been proposed to tackle the problem of secure multidimensional range queries. Lu [7] proposed a range search scheme on encrypted data by leveraging predicate encryption and B+ trees. He extended the original scheme to support multi-dimensional range queries by replacing B+ trees with kd-trees in the implementation. Wang et al. [8] presented a scheme for evaluating multi-dimensional range queries by using asymmetric scalar-product preserving encryption and R-trees. However, these two methods lead to single-dimensional privacy leakage.

Bucketization-based scheme. Bucketization-based data representation for query processing in an untrusted environment was originally leveraged by Hacigumus et al. [9]. Their bucketization simply involves a data partitioning step based on equi-depth or equi-width partitioning to support single-dimensional range queries. The queries are mapped to a set of buckets that contain any value satisfying the range of the query. The original queries are translated into bucket-level queries, which request the encrypted buckets containing the desired values. Several studies have attempted to reduce bucket costs (i.e., false positives) while preserving the anonymity of the data set [10]. Hore et al. [11] extended the bucketization-based method to support secure multidimensional range queries. Their method tries to cluster d-dimensional space into various hyper-rectangles, and bucket indexing is performed on the clustered hyperrectangles.

Order-preserving encryption based techniques. An order-preserving encryption scheme is a deterministic cryptosystem whose encryption algorithm produces ciphertexts that preserve the numerical ordering of the plaintexts. Roughly speaking, for any two ciphertexts c 1 and c₂ corresponding to plaintexts p 1 and p₂, respectively, if p 1 < p₂, then it is guaranteed that C 1 < c₂ . Orderpreserving encryption was first proposed by Agrawal et al. [12] to support range queries on encrypted data. When the dataset is encrypted by an order-preserving encryption scheme, the result of a single-dimensional range query is simply determined by the encryptions of the two endpoints. The concept of order-preserving encryption was efficiently revised with formal security analysis by Boldyreva et al. [13] [14] and Mavroforakis et al. [15]. Although these techniques are highly efficient, they provide weak privacy. As such, traditional efficient indexes can be built directly on encrypted data and queried in the same manner as plaintexts. Nevertheless, order-preserving encryption is deterministic and hence suffers from inherent distribution leakage. In addition, it inevitably leaks the ordering of the data.

• B.    Oblivious RAM

Oblivious RAM (ORAM) is a cryptographic primitive that conceals memory access patterns. The idea of ORAM is to continuously reshuffle the memory and translate the address of each memory access to a set of randomized memory locations.

ORAM was first investigated by Goldreich [16] using the “square-root” solution. The objective was to address the problem of software protection, i.e., to prevent unauthorized copy. Goldreich’s solution partitions the server memory into two regions: a main region of O(N) blocks and a shelter of (OVN ) blocks. Each access involves linear scan in the shelte r region and one access to the main region. After (OVN) operations, the data structure is reshuffled. Goldreich and Ostrosvky [17] presented the well-known “hierarchical” solution to achieve polylogarithmic memory bandwidth overhead. The key idea of this solution, in contrast to Goldreich’s above-mentioned solution, is to organize the server memory into a hierarchy of buffers whose sizes grow at a geometric rate.

A recent breakthrough was made by Stefanov et al. [18], who mapped each data block to a random path of a binary tree. The information for the path of each data block is stored in a position map. To access a block, the client first looks up the position map and reads all the buckets on that path. Each data access requires O(log²N) memory bandwidth overhead. The solution requires O(N) local data storage for the path of each data block. Shi et al. [19] proposed ORAM recursion to reduce the client storage to O(1). The key idea is to store the position map on the server side as a second ORAM. This may be performed recursively until the client storage is O(1). Clearly, the access operation now includes looking up all the position map ORAMs in addition to the main data ORAM, which increases the bandwidth overhead to O(log³ N). Stefanov et al. [20] proposed an extremely simple and efficient ORAM protocol called Path-ORAM. Path-ORAM is the first technique to achieve O(log N) memory bandwidth overhead under small client storage. In this paper, we refer to the Path-ORAM design when the ORAM technique is used.

• III.    Problem Formulation

We consider a scenario involving a data owner Alice. Alice possesses a multi-dimensional dataset D of n records. Each data record has m numerical attributes. Let a , denote the identifier of the i-th attribute and x j denote the value of the j-th attribute of the i-th record.

Alice wishes to outsource her dataset (i.e., the set of data records) to a cloud server to save local storage costs. A typical example is the data of body measurement recorded by sensors or mobile devices. Because mobile devices are normally limited in terms of storage capability, outsourcing such information to cloud services offers easy and low-cost solutions for long-term continuous health monitoring. On the other hand, such data include confidential personal information; hence, they should be stored in an encrypted form. At the same time, to facilitate health monitoring and treatment, the data owner needs to use the outsourced data efficiently.

To query the outsourced dataset, Alice performs a multi-dimensional range query. A multi-dimensional range query is a process of retrieval of data records that satisfy query values from the relative attribute domains:

Select * from D where a_x. £ [s_z , t^.] , x_te S g £ {1,-,m} .

Let [a,b] represent an interval of integers from a to b, inclusively. The set of attribute identifiers S_g = {xf is called the set of queried attributes . A multi-dimensional range query requests data records such as each attribute V j in the set of queried attributes . Note that S_g takes values in the interval [5_X., t_x.\ . Roughly speaking, each data record can be considered as a point in m-dimensional space, and the multi-dimensional range query is defined by a hyper-rectangle. All the points inside this hyperrectangle are considered as the results of the query.

When the set of queried attributes covers all m dimensions of the database D: S_g = {X j } = {1, "-.m}, we say that the query is a full-domain query. Section V discusses the solution for this scenario. Section IV discusses viable solutions where the query's dimensions change dynamically from one query to another, with no fixed set of the concerned attribute domain for the query. Although studies have been conducted to address such a multi-dimensional query, they require the data owner to share his/her private key with a semi-trusted third party, which is not practical owing to privacy threats. In Sections IV and V, we will discuss the solutions in the settings of static and dynamic data storage. In the static database settings, the data owner uploads the entire data only once and is later able to query for the necessary records. On the other hand, in the dynamic database settings, new data records can be appended to the previously uploaded data, and expired data can be transferred to archive data storage and removed from the query results. We assume that the three parties loosely synchronize the time of archiving the data.

• IV.    System Models

• A.    System Model

We adopt a three-party architecture described by Boneh et al. [21] and Cristofaro et al. [22]. The system consists of three parties: the data server, the client, and the index server (see fig.1) .

• 1.    Client :  possesses a numerical multi-dimensional

• 2.    Data server : provides storage services to the client. The cloud server is trusted to provide reliable services but it may also be curious about the content of the

• 3.    Index server : stores meta-data to support answering of the query. As with the data server, it is trusted to store the meta-data as well as correctly process the query initiated by the data owner. In addition, it may be curious about the client’s data as well as the query content.

dataset and wishes to outsource his/her dataset in encrypted form to the data server. At some point, he/she should have the capability to securely construct a multi-dimensional range query to obtain the requested data.

data records stored in its database or the content of the queries submitted by the data owner.

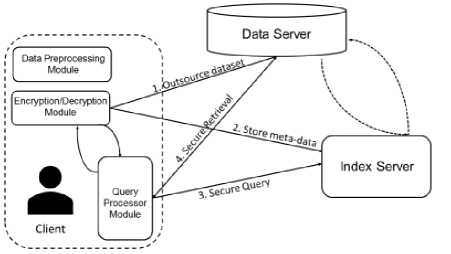
Fig.1. System Architecture

Workflow . Based on the notation in fig.1, the workflow of our system can be described as follows. The data are first preprocessed by the data preparation module on the client side. The dataset and the meta-data (i.e., output of the preprocess phase) are encrypted by the encryption/decryption module and sent to the data server and the index server. The entire dataset should be encrypted by a symmetric encryption scheme. It involves low overhead for data storage and bandwidth, as well as efficient encryption/decryption operations. On the other hand, the meta-data should be encrypted by a specific public key cryptosystem and embedded in a special data structure to enable secure query processing.

To construct a multi-dimensional range query, the client constructs the query content using the query processor module, which has an interface with the encryption/decryption module. The encrypted query content is sent to the index server. The index server will output the corresponding indices of the satisfied data records so that the client is able to efficiently retrieve them from the data server. Further, the query processor module may be invoked to filter the results returned from the data server.

• B.    Security Assumptions and Requirements

In this paper, we assume that the user, cloud server, and index server are semi-honest. The servers will correctly follow the protocol specification; however, at the same time, they are also curious about the user’s plaintext data. In addition, we assume that there is no collusion between two participating parties to access the user’s confidential data. We emphasize that this assumption is realistic under the cloud environment. At present, with the development of cloud services, it is difficult to consider the possibility of collusion by well-established cloud service companies, which would damage their reputations and consequently have a negative impact on their revenues. In this work, we attempt to design a secure multi-dimensional range query while preserving the privacy of the database content and query values. Ideally, a secure protocol should only reveal what is leaked by the system parameters known to all parties and by the intended functional output. More specifically, we consider the following information leakage:

• 1.    Data Privacy. A passive attacker who gets a snapshot of the encrypted database and encrypted index data should not be able to obtain any information about the user’s private data. This implies that these two types of data should be encrypted by a probabilistic cryptosystem.

• 2.    Query Privacy. The cloud and index servers should not be able to determine whether two queries are the same.

• 3.    Access Pattern. Access to satisfied data records should not be revealed to the cloud server. Islam et al. [23] showed that data access pattern leakage could lead to the disclosure of a significant amount of sensitive information.

• 4.    One-dimensional Privacy. Informally, singledimensional privacy means that given a search token of a multi-dimensional range query, a computationally bounded adversary is not able to independently obtain the exact search results for any single-dimensional query.

While allowing the user to download the entire database and performing the query locally will achieve all the above-mentioned privacy requirements, this solution is infeasible. The proposed solution should be efficient in terms of time complexity, communication, and round complexity.

• V. Full-Domain Multi-Dimensional Range Query

First, we describe the construction of full-domain multi-dimensional range queries. The dataset contains multiple data records that are points {x,}”_ 1 in a m-dimensional lattices. A full-domain query is defined by a hyper-rectangle in the m-dimensional space:

B = {[S1,t1],[S2,t2],^,[Sm,tm]} where [s/, tj] represents a single-dimensional range. A data record {x,}^ satisfies a query represented by the hyper-rectangle B if and only if Xj £ [s, , tj] for V j: 1 < j < m.

As mentioned above, each record of the dataset is encrypted individually by a symmetric encryption scheme such as AES. This allows for efficient retrieval of specific records from data server. Hence, this work focuses on designing the data structure and algorithms to find the indices of data records that satisfy the query criteria. Specifically, we present a method for constructing the meta-data, the data structure to store the metadata at the index server, and the algorithms to process the query. Our solution for the full-domain multi-dimensional range query problem is inspired by the multi-dimensional bucketization approach. First, we partition the data space into M disjoint buckets. The number of buckets M is smaller than the number of data points n. Each data record belongs to exactly one bucket. The query processing translates into the problem of retrieving the bucket content. Hore et al. [11] claimed that nondeterministic encryption of the bucket labels does not raise the level of security, because simply encrypting bucket labels cannot protect the query privacy or access pattern from an adversary. In this paper, we leverage the ORAM technique to hide the access pattern and thus provide a stronger security guarantee.

• A.    Solution Overview

The dataset is first pre-processed by the data preprocessing module. It is partitioned into nonoverlapping buckets, and the bucket label is set as the tag for each data record in the bucket. The data owner encrypts each original data record (i.e., a d-dimensional data point) and uploads it to the data server. Furthermore, an encrypted inverted index table is stored at the index server in the following form:

( Bucket Label, encrypted set of record indices )

The idea of the solution is to leverage ORAM data access for each intersecting bucket without leaking any information about the data or the query content. The satisfied records are determined by buckets intersecting the query. Many existing studies have indicated that ORAM is impractical owing to its high computational cost. However, this claim is not necessarily true, especially because nearly all existing studies focus only on designing various methods to retrieve the indices of the satisfied records while leaving the actual data retrieval process to a black box. The black box is assumed to be a standard ORAM protocol for data records with known indices. It contradicts the abovementioned concerns with regard to practical application. Recent results on Path-ORAM have shown that it is a practical tool for data access. When the record indices are known to the client, a constant number of communication rounds of ORAM data access should be required to retrieve the data.

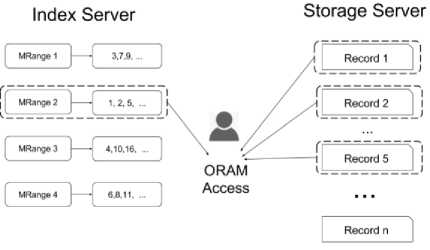
Fig.2. Secure Multi-dimensional Range Query from ORAM

The two main challenges faced by this approach are how to partition the space into buckets and how to embed the record indices into the ORAM data structure stored at the index server.

Bucketization algorithms. We retrieve a bucket if and only if it overlaps the query rectangle. We partition the space into M non-overlapping hyper-rectangles. Each rectangle contains approximately the same number of data points. The parameter M is determined by the tradeoff between the cost of false positives and the cost of communication between the client and the index server. When the number of buckets increases, each bucket contains fewer points, and the false positive rate decreases. However, the number of buckets intersecting with the query increases, which means that the number of ORAM accesses increases. On the other hand, when the number of buckets decreases to one, fewer ORAM accesses are required for each query. Further, when the false positive rate increases, additional bandwidth overhead is incurred to retrieve the actual data records from the server. With a certain parameter M, we use the Mondrian multi-dimensional partition algorithm presented by LeFerve et al. [24] (see Algorithm 1). In this protocol, we assume that M = 2^k for simplicity.

Algorithm 1: Partition) D, M)

Input: Dataset of multidimnensional points D, number of bucket M = 2^k

Output: M buckets i attr —>!,■-- , m ;

• 2    splitVal -> find_median(D,attr) ;

• з    left_half —r {r G D : r.attr < splitVal) ;

• 4    right_h,alf —> {r G D : r.attr > splitVal);

s return

Partittcm,(left_half, Mf2) |J Partition(right_hal f, M/2)

At each call, the algorithm partitions the space according to the value of attribute attr , which is chosen at step 1. The data space is partitioned into two parts. Each part has approximately the same number of elements. The complexity of the preprocessing phase is O(log n).

ORAM storage. Each data label is associated with a list of record indices. Our solution stores these indices in the ORAM data structure so that we can secure access to the content of a particular bucket. A naive solution is to use a sufficiently large ORAM data block to store the entire set of encrypted record indices. The user can retrieve the entire set of indices for a block label at once. However, because the size of the index set of each bucket label may vary, it is wasteful to use a large-sized data block to store a small piece of information. Moreover, it is computationally expensive to read from and write to a large-sized data block. Our approach is to represent the index sets in a compact form so that the data ORAM block can be determined beforehand with reasonable size.

• B.    Static Dataset

First, we consider the simplest scenario where the dataset is intact after uploading to the server. Archiving data is an example of this scenario.

The dataset is preprocessed and encrypted once before being uploaded to the data server. In the preprocessing stage, the bucketization algorithm (Algorithm 1) is applied to partition the space into buckets. Each record (i.e., a data point) belongs to exactly one bucket. Data are rearranged so that the identifiers of data records in the same bucket label form a consecutive numerical counter. Hence, the necessary information to reconstruct an index set is the starting counter and ending counter. The metadata stored at the index server are ORAM data structures such that each block has an encrypted bucket label as the key for the encryption of the starting counter and ending counter as the values. Hence, to query for a data bucket, the data owner performs an ORAM data access with the index server; the access key is the bucket label. Then, the client obtains the range of data identifiers. The last step is to perform one more round of data access for each data identifier with the data server.

Analysis. Because the data and their indices are encrypted on the client side by a standard secure cryptosystem, the data server and index server obtain no information from the view of the stored data. Furthermore, the data owner accesses the index data at the index server and the data content at the data server by means of ORAM. The two servers are not able to obtain additional information of the query content or the access pattern. Because the data are obtained by the bucket label, onedimensional privacy is satisfied for the query.

The bandwidth overhead of the solution is O(log n) owing to the overhead of Path ORAM. The client is also required to maintain a local storage of O(log n) . Finally, the complexity of each data access incurred at the server is O(log n).

We also note that in the case of the static dataset, private information retrieval (PIR) can be used as an alternative to ORAM. In the PIR approach, for reading data, the computational complexity for the data owner is linearly related to the size of the retrieved data; in terms of the server size, the computational cost is linearly related to the size of the entire data set.

• C.    Dynamic Dataset

We consider the case where the update operation is allowed. More specifically, new data records may be appended to the existing dataset. Log file is an example of this scenario.

Because the new data records can be in any data bucket, we cannot use the previous approach. In the abovementioned approach, the indices of data records in the same bucket label are required to form consecutive integers. Because the new records are not necessarily in the bucket containing the previous records, this requirement does not hold. We adopt another approach to index the records. We make use of the collisionresistance hash function. The index of a new record is determined by the hash of the previous record index that is in the same bucket. More specifically, we consider a collision-resistant hash function h: {0,1} ” ^ {0,1}^m and define a sequence generated by h as follows:

a₀ = label - Id,    a_f = hQa-).

To obtain the index set of the bucket label for the i-th bucket, we need to know the values of a 0 and a ” , where a ” is the last element in the sequence generated for data records belonging to the i-th bucket. In this case, when the data are appended, the data owner is required to modify the corresponding ORAM data block to update the last element of the current index set. On the other hand, to obtain the index sets of buckets intersecting the query, the data owner retrieves the corresponding block to get Enc(a 0 ) and En^a ” ) . Further, the data owner decrypts the encrypted content and iteratively generates the sequence starting from the first element until the last element using the formula a , = h(a_i-1). A collisionresistant hash function is required for this construction so that different data records are not mapped to the same index.

To insert a new record into the data set, the data owner first determines the bucket label of the new data record. Next, he/she performs a read and an update operation with the index server by means of ORAM. The new content of the ORAM block now contains the encrypted next sequential number of the last record index in this bucket.

Analysis. We use a collision-resistant hash function to index the records because each data record belongs to exactly on data bucket. Moreover, it is difficult to find a collision; each data record has a unique identifier determined by the hash functions.

The security of the dynamic case construction is analyzed in the same was as that of the static case. In both cases, the user accesses the indices and the real data records using ORAM. Hence, the only information leakage to the cloud server is the result size, which is the lower bound of the number of satisfied records. The reason is that the user is required to make at least the minimum number of satisfied record ORAM data accesses to the cloud server data.

The complexity and bandwidth overhead of the solution remain polylogarithmic owing to the use of Path ORAM. The update operation as an ORAM write operation also requires O(log n) memory bandwidth and computational complexity.

• VI. Dynamic Multi-dimensional Range query

The aforementioned approach can be generalized to address the scenario in which the set of queried attributes is fixed. Roughly speaking, we should be able to efficiently represent the query space by a small number of fixed hyper-rectangles. In this section, we examine a more general case where the set of queried attributes varies for different queries. In other words, the number of dimensions in each query can vary from one to $m$ - the number attributes in each data record. Clearly, we can treat the query as a full-domain query by considering each missing dimension as the full range. However, this approach normally leads to an excessive number of communication rounds with the index server. Instead of using the multi-dimensional bucketization technique, we apply the single-dimensional bucketization approach as a solution to this generalized problem.

A general multi-dimensional range query is defined by an unordered set:

в = {[Si1,ti1],[Si2,ti2],-,[Sik,tik]}

• 1    < i j < m , and [s /y , t/^ represents a singledimensional range. The size of the set of queried attributes is k, 1 <  к < m.

• A.    Solution Overview

Our solution for the generalized problem employs private set intersection techniques. First, we partition each single-dimensional domain into buckets. A data record of m attributes falls into m buckets. For each single-dimensional range in the query, the requested data records must belong to the buckets intersecting with the range. A naive solution is to perform multiple queries on each queried dimension. The results are the intersection of the results. This approach has been used by Zhang et al. [25] to design multi-dimensional range queries in sensor environments. However, the naive approach fails to provide single-dimensional privacy because the server gains the results for each queried dimension. In this paper, instead of performing the intersection operation on the client side, we conduct it on the server side in a privacy preserving manner.

The query is firstly decomposed to each corresponding dimension. For each queried dimension, the intersecting buckets are enumerated. The query now can be translated into the one or multiple conjunctive queries. The variables in the conjunctive query are intersection buckets in each dimension. Finally, secure set intersection algorithm should be applied to answer the conjunctive query.

To illustrate our idea, we consider the following example. Alice has a dataset where each data record is a three-dimensional point (x, у, z). The attributes receive integer values in the domain [1,10]. Alice decomposes the data space with eight buckets: [0,5]_ж,[6Д0]_ж,[0,5] у ,[6Д0] у ,[0,5]^^ . Each record is in exactly three buckets. Alice wishes to perform a simple multi-dimensional range query: 3 < x < 6,2 < у < 4. The query can be transformed into two conjunctive queries: [0,5]_x л [0,5]_y and [6,10]_x л[0,5]_у . Query [0,5] ^ л [0,5]_y (similar for the other) is translated as retrieving all the data records belonging to both [0,5]_x and [0,5]_y. The answer for it is the intersection between two buckets.

Bucketization algorithms. We apply a simple equidepth bucketization approach to partition each dimension for the data space. The number of buckets M in each dimension is determined by the tradeoff between the number of conjunctive queries and the false-positive rate. If we partition the dimension into many small buckets, we are able to reduce the false positive rate of the results. On the other hand, if M in each dimension is small, we are required to perform fewer conjunctive queries but additional work is required for the post-processing.

We now describe the method for securely answering each transformed conjunctive query in two different settings.

• B.    Static Dataset

For the case of a static dataset, the entire dataset is processed and uploaded only once to the servers. We leverage the Kissner-Song private set intersection [26] to perform conjunctive queries.

The idea underlying the Kissner-Song protocol is to fix a large field F and represent a set Sc F by a polynomial A_y that has zeros in all the elements of S, i.e., Д у (x) = O se _y(x — s). To compute the intersection of many sets S / , we construct a polynomial В whose zeros are the intersection of these sets. Clearly, if a point s e F is contained in all the sets S / , then A_y. (s) = 0 V i, and therefore, if we compute B as a linear combination of A_y.’s, then B(s) = 0. On the other hand, if A_y.(s) ^ 0 for some i and B is a random linear combination of A_y. ’s, then B(s) ^ 0 with high probability. Roughly speaking, instead of storing the record indices for each bucket, we store the coefficients of the polynomial that represents the index set. However, the coefficients should be encrypted so that the index server is not able to trace the indices.

In this paper, we use the BGN encryption technique [5] to encrypt the polynomial coefficients. The BGN cryptosystem, proposed by Boneh, Goh, and Nissim, allows both additions and multiplications with a constant size ciphertext. However, there is a catch: while the addition can be performed multiple times, only one instance of multiplication is permitted. Nevertheless, this protocol is considered to be much more practical than fully homomorphic encryption schemes. The homomorphism allows us to compute a linear combination of the polynomial in encrypted form so that set intersection operations can be securely performed on the index server.

Let Gen., Eire, Dec denote three BGN cryptosystem algorithms: key generation, encryption, and decryption. We have the following properties:

•    Gen: generates a key pair (pk, sk) where pk and sk are public and private keys, respectively. •    Dee(Ene(m)) = m for m in the message space. •    Add(pk,Ene(x),Ene(y)) = Ene(x + y) can be performed multiple times on two encrypted values Ene(x) and Ene(y). •    Mul(pk, Ene(x), Ene(y)) = Ene(x ■ у) can be done only once.

Consider a bucket consisting of I data records with indices i 1 , —, i # . It can be represented by a polynomial of the form A(x) = (x - i 1 ) — (x - i # ) = £ e_i x xⁱ. The coefficients e / of the polynomial are encrypted by a BGN cryptosystem and stored at the index server. The index server stores m x M encrypted polynomials, where M is the number of buckets for each dimension and m is the number of attributes in each data record.

To issue a multi-dimensional range query (i.e.,

Q = {[s^t/J,---, [s/k,t/J}    ), the client first decomposes the query into к dimensions: i1, i2, — ,ik. The query is transformed to multiple conjunctive queries; each one is associated with к buckets corresponding to к dimensions. To obtain the answer for each conjunctive query, the client does the following:

• 1.    We consider a bit b / = 1 if the i — th bucket intersects with the query (0 otherwise). There are exactly к encryptions of bit 1 for each conjunctive query.

• 2.    The client generates appropriate tags, (Т / = Enc(b / ), and sends т / to the index server.

• 3.    The index server generates random non-zero numbers p / and computes S(x) = Е / Т / X p / X А / (in encrypted form), and sends the corresponding result to the user.

• 4.    The client decrypts and factors the polynomial S(x) and finds its roots, which are the indices of the records that are of interest to the user.

• 5.    The client performs ORAM data access to obtain the necessary data records from the cloud server.

Analysis. To analyze the security of the proposed protocol, we need to examine the data view of the two servers. Because the server stores securely encrypted data, and the data are accessed only by ORAM, it gains no knowledge of the user sensitive data, query content, or access pattern. Moreover, the index server receives only BGN-encrypted bits; it is not able to obtain any information about the query. Hence, the proposed protocol leaks no information of the data content, query content, or query result to the server or the index server, except for the upper bound of the number of matching records (owing to the number of ORAM accesses).

The proposed solution requires the client to send О (m X M) encrypted bits to the index server and receive approximately 0(n/M) bits from the index server. At the same time, the index server is also required to perform up to 0(n) multiplication and exponentiation operations in the ciphertext space. The computation and communication costs for the server are the same as those of the previous methods.

• C.    Dynamic Dataset

In the dynamic dataset case, the new data records may be dynamically appended to the existing dataset. The aforementioned approach, which represents the index sets by polynomials, requires the entire encrypted coefficients for each corresponding bucket of the new record to be recomputed. We propose another approach that requires interaction between the server and the index server. We note that the abovementioned methods for both fulldomain queries and dynamic multi-dimensional range queries do not require any communication between the two servers. The proposed protocol is inspired by a conjunctive keyword searchable encryption protocol proposed by Cash et al. [27]. We use it with a major modification to adapt our privacy requirements.

We start the protocol description by reviewing a few concepts related to bilinear maps. We will use the following notation:

• 1)    G 1 and G 2 are two (multiplicative) cyclic groups of prime order p.

• 2)    g 1 is a generator of G 1 and g₂ is a generator of G 2 .

INSERT (Record id:: x = (xy • •, x ™ } )

• •    For each i — th dimension (1 < i < m), the client does:

• ■   Let j — th bucket of i — th dimension:

bucket l^]_t contains attribute value X / .

• ■   Compute    xind ^ F_Kl(id"), z^ F_Kz(l{')

xind and у ^ gr z

• ■    Set eid ^ Enc(id) , append (eid, у) to a list for bucket l^]_t at index server.

• ■    Set xtag ^ e(g₁,g₂)^t'^FKx^¹^' ^xmd)    and

append to a set S at cloud server.

• •    Encrypt the data record and upload the cloud server.

SEARCH ( Q = { [s/1 ,t,J.....[s„,t,J})

• •    Client decomposes the query into к dimensions: i 1 , i₂,..., i_k . The query is transformed into conjunctive query of buckets. For each conjunctive query q, we denote the buckets of interest for these к dimensions as L 1 ,..., L_k.

• •    For i = 2, .,к:

• •    Client computes xtoкen_/ ^ д^^ ' ^FKx(Li)

• •    Client sends L 1 , {xtoкen₂, — , xtoкen_n} to the index server.

• •    For each item (eid, у) in L 1 list in random order:

• ■    Index server sends eid to the cloud server.

• ■    Securely compute the cardinality size of the intersection between set S at the server and {e(у,xtoкen₂), ..,e(y,xtoкen_k)}

• ■    If size = к — 1 , the cloud server sends eid to the client.

• •    Client decrypts and obtains the indices.

• •    Client performs ORAM data access to obtain the necessary data records from the cloud server.

A bilinear map is a map e : G 1 X G 2 ^ G_T with the following two properties:

• 1)    Bilinear: for all u £ G 1 ,vE G₂ , and a,bE Z , e(u^a,v^b) = e(u, v)^ab .

• 2)    Non-degenerate: e(g 1 ,g₂) ^ 1.

The proposed solution consists of two algorithms: INSERT and SEARCH for appending new records and performing multi-dimensional range queries on the encrypted data set respectively.

The correctness of the search protocol relies on the following fact:

e(y,xtokenj) = e^^g^ ^FKx(Ll)) Fk^D

= e^^Wt^’^^

= e(g i ,g₂)^FKi^(ldyFK x⁽^ ¹

Hence, if the set [e(y, xtoken₂), ...,e(y, xtoken_k)} is a subset of set 5 , the data record belongs to exactly all the requested buckets.

Our construction of the index list for the bucket and for the set S are similar to the construction of TSet and XSet proposed by Cash et al. [27]. In their protocol, TSet and XSet are stored in the same place in the cloud server. The correctness and the privacy of the two sets follow the proofs of the authors, given in [27]. However, because the set intersection is performed locally by the cloud server, that construction leads to unnecessary information leakage (i.e., access pattern). In the proposed construction, the storage of the bucket list and set S is separated into two parts, and the set intersection cardinality is obtained by a secure two-party computation protocol. We apply the protocol proposed by Cristofaro et al. [28]. Fig. 3 shows the workflow of the protocol. The protocol is secure under semi-honest model assumptions. The complexity is linearly related to the sizes of the two sets.

Fig.3. Secure set Intersection Cardinality

Analysis . The insertion algorithm only appends the semantically secure encryptions to the server and index server. It leaks no information to the two servers; for details of the proof, readers may refer to [27].

During the search phase, the server only receives the encryption of the record index eid and knows whether the encrypted index belongs to the results. By observing the value of eid, the server is able to determine whether there are records that satisfy multiple queries. This information leakage can be eliminated by applying one more encryption layer on eid.

On the other hand, the newly proposed protocol does not provide query privacy to the index server. The index server is able to determine whether two queries are the same by observing the xtoken sets received from the client. However, this is the only information leakage of the client’s private data to the index server. Because the cardinality of private set intersection is only revealed to the cloud server, the index server does not obtain any information about the satisfied records.

The computational complexity and communication cost of the two servers are linearly related to the number of data records. The communication cost and computational complexity for the client are O ( max ( log | D | ,n )), where | D | is the number of data records and n is the dimension of the query Q .

• VII.    Experimental Results

We conducted a number of experiments to verify the practicality of the proposed solution. The experiments were performed on a synthetic dataset. We created the synthetic dataset by sampling 20,000 data points, each having 4 integral attributes from the domain [0,999].

Our implementation of Path ORAM requires up to 2 minutes to construct the ORAM data structures of the dataset of 10,000 data records. It also only takes only 0.02 s per access, including the time for decryption. This execution time is considered as a criterion for the tradeoff between the accuracy and the number of buckets, as discussed in Section V. For full-domain multidimensional range queries, we randomly generate 10,000 queries where each dimension is selected randomly from a uniform distribution from the same domain with the dataset. We took the average results of these queries and reported them.

Consider the number of buckets M. The accuracy of the intersection bucket approach is 0.1,0.15,0.3,0.5 for M = 128,256,512,1028 , respectively. On the other hand, the numbers of buckets intersecting with the query are 22,33,53,107 for each configuration of M. Thus, when the parameter M increases, we are able to reduce the false-positive rate; however, we need to perform additional ORAM queries with the index server.

To test dynamic multi-dimensional range queries, we considered 5000 random queries. T he set of queried attributes contains 1–3 attributes. The two end points of each query are uniformly generated from the attribute domain.

Fig.4 shows the relation between the accuracy of the proposed approach and the number of buckets in each dimension (M). We conducted experiments with M in the range of 5–20. When we used only 5 buckets per dimension, the reported false positive rate was high, but we were only required to perform 5 conjunctive queries on average for each query. On the other hand, when we increased M to 20, the accuracy increased to 70%. However, we also needed to answer 60 conjunctive queries (i.e., depicted Fig.5) to obtain the complete set of requested records.

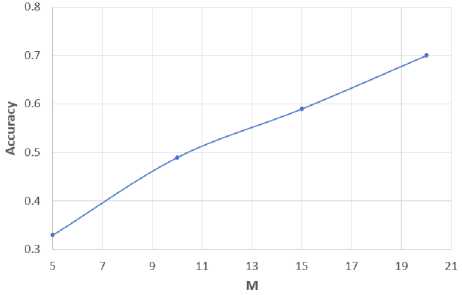
Fig.4. Accuracy for Different Numbers of Buckets (M)

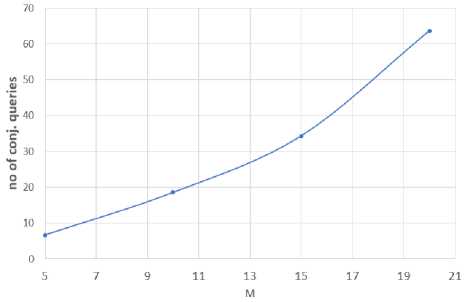
Fig.5. Number of Conjunctive Queries for Different Numbers of Buckets (M)

• VIII.    Conclusion

In this paper, we investigated different protocols to securely evaluate multi-dimensional range queries over encrypted data in cloud platforms. Our main idea is to leverage the bucketization algorithm to label the numerical range. The server stores the encrypted data, while the index server stores the meta-data output by the bucketization algorithm. When the multi-dimensional range queries are fixed beforehand, we perform two rounds of ORAM data access to answer the queries. The data records are labeled before encryption and sent to the server. On the other hand, to support more general queries, we presented novel solutions that allow multidimensional range queries to be answered, where the query constraints are not required to be fixed. The idea is to bucketize each attribute of a multi-dimensional data record and perform set intersection to answer conjunctive queries for multiple data labels. While the latter approach is able to support more general requirements, it is costly in terms of both computational complexity and bandwidth communication. In the most general case, where the dataset can be dynamically appended and the set of queried attributes is not fixed, our approach leaks a small amount of information to the index server.