Multi-layer Masking of Character Data with a Visual Image Key

Published Online October 2017 in MECS DOI: 10.5815/ijcnis.2017.10.05

The project includes a working application developed in Visual Basic 6.0, mainly for the purpose of demonstration and harnessing VB’s inherent rapid development features.

Cryptology is the field where mathematics and security engineering enmesh together to give us tools to protect systems and information. In a very basic sense, Cryptography is the art and science of designing algorithms for performing encryption, while Cryptanalysis refers to the science and arts behind breaking them. Cryptology encompasses the study of both Cryptography and Cryptanalysis.

In today’s modern world, Information Security has become the most talked about field in computer science, which clearly underlines the gravity of cryptology and its related studies. Cryptology has been in use since the time of Roman emperors [1]. Julius Caesar enciphered A for D, B for E and so on. In modern parlance, it is said that the key had been altered from D to A.

However, Arabs are the most prominent for developing a systematic approach of cryptanalytic methods. Al-Kindi, an Arab mathematician, sometime around AD 800 invented the technique of frequencyanalysis for breaking monoalphabetic substitution ciphers, which was a significant valuable resource on cryptanalytic field till World War II [2]

Leon Battista Alberti, the Italian Cryptographer, conveniently known as the “father of Western Cryptology”, is the first individual to bring forth the Polyalphabetic Cipher, which is significantly stronger methodology from that of the earlier monoalphabetic crypto algorithms [3].

Gilbert Vernam in 1917 proposed a teleprinter cipher. The method included using a previously prepared key, kept on paper tape, to combine with each of the characters of the plaintext message in a view to produce the cyphertext. This led to the development of electromechanical devices as cipher machines, and to the only unbreakable cipher known as, the one time pad ^[5].

Claude Shannon’s “A mathematical theory of cryptology”, written in 1945, is considered by most as the inception of the development of current cryptologic advancements [6]. Modern encryptions are designed by employing algorithms having a key to encrypt and decrypt information. The role of these keys are to change the original message and data into seemingly nonsensical data or gibberish thorough encryption and then retrieve the bona-fide through decryption. The critical factor here is the key length, which is directly proportional to the degree of difficulty of breaking the encryption.

• II.    C lasses of C ryptosystems

The data/information that needs to be encrypted are known as Plaintext, while the output to encryption function is called Ciphertext. Depending upon the algorithm, there are number of cryptographic primitives such as Stream Ciphers, Block Ciphers and Hash Function.

Block Ciphers

A block cipher is an encryption method which encrypts the inputted information as a block of data (for example, 96 contiguous bits) at once as a group instead of one bit at a time. Blocks are of fixed size bytes which can be up to 128 bits long. The block cipher can encrypt, for example, a 128 bit plaintext and generate a 128 bit cipher text as the output result. In order for a block cipher to encrypt data, the function would require a secret key which comes as a string of bits normally 128 to 256 bits long. A preferred block size is a multiple of 8 as it is easy for implementation as most computer processor handle data in multiple of 8 bits. As all the blocks need to be of same size, the last block, if necessary, is padded up to the length of desired bits [7].

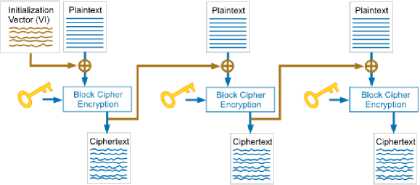
Fig.1. A Graphical Representation of Block Cipher Algorithm

Some of the more popular Block Cipher Encryption systems are Digital Encryption Standard (DES) – gained lots of ground in 90s, Triple DES – A variant of DES, Advanced Encryption Standard (AES) – a newer block cipher algorithm and IDEA – another modern block cipher application with wide acceptability and has a sufficiently robust encryption capability.

Stream Ciphers

This types of encryption algorithm encrypts a single bit or bytes of plain text at a time. It applies a pseudorandom cipher digit stream (keystream) on each bit of the message to be encrypted. For a stream cipher implementation to remain absolutely secure, its pseudorandom generator has to be unpredictable plus the key should never be reemployed.

Plaintext bib

Keystream bits

□□□□□□□

Ciphertext bits

Fig.2. A graphical representation of Stream Cipher Algorithm

One-Time Pad: Encryption

|meei me or rsioi:|

amjraiiWEtumss m x\h лики мл iku mhuirmu или wninvrirvs.T A HXM^USVl'l our NSJSKA№>rmW|> I hue!

Plaintext:	M	E	E	1	M	E	о	и	T	s	I	D	E
Numerical Plaintext:	12	4	4	19	12	4	14	20	19	IN	s	3	4
OTP:	В	0	I	F	G	H	w	E		H	F	G	W
Numerical OTP:	1	3	20	5	6	7	22	4	8	20	5	6	22
Numerical Ciphertext:	13	7	24	24	18	n	10	24	1	12	13	9
Ciphertext:	N	I!	Y	V	S	1.	К	Y	В	M	N	J

4 + 22 = 0 modular 26

Fig.3. One Time Pad Encryption Algorithm

However, one time pad did not get wide implementation due its key-length issues, which can sometimes be extremely large. However, one algorithm that did get wide popularity is RC4 (Rivest Cipher 4). RC4 has been used in wireless network security protocols such as WEP and WPA. Besides RC4, which has recently lost some grounds, other stream cipher systems such PANAMA and SALSA may come into foreground.

Hash Functions

Hash functions, first used around 1960 in computer systems, these days have become extremely important and useful in many sorts of applications. Hash functions are mathematical functions that convert a numerical input value into another numerical value, often compressed. The input to the can be of arbitrary length whilst the output is always of fixed length. The encrypted values are often known as Hash values or message digest as the content is considerably smaller than the inputted data. The process of converting the raw data to a message digest is known as Hashing. Hash functions are computationally faster than symmetric algorithms such as block ciphers. Hash functions have few fundamental properties such the easiness of calculating the hash for any given data, the extreme difficulty of reversing the process and having the same hash for different data, as a slight modification in the original data entails a great change in the hash itself [9].

Stream ciphers can often be designed to attain the allusive characteristic of “Perfect Secrecy”, one such example of an encryption system is the “One Time Pad”. It’s a technique that cannot be broken, but needs the use of a one-time key which is pre-shared, the key is of the same size, or longer, as that of the message being sent. To begin with, a plaintext is paired with a random secret key (also denoted as a one-time pad ). Then, each bit or character of the plaintext is encrypted by combining it with the corresponding bit or character from the. Now if the key used, kept completely secret, is truly random, and at least as long as the plaintext, also if never reused in whole or partially then the resulting ciphertext will be impossible to crack ^[8].

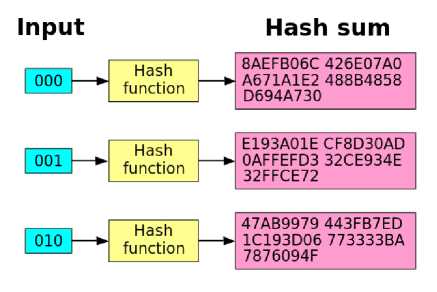
Fig.4. Changing of Just a Single Bit Can Bring a Considerably Change in the Corresponding Hash Value

Some popular Hash encryption systems are Message Digest 5 (MD5) and Secure Hash Function (SHA). Storage of passwords and verifying data integrity are two most widely used applications of Hash functions.

Public-Private Encryption

In a revolutionary 1976 paper, W. Diffie and M. Hellman brought forward the notion of Public-Key cryptography in which two different but mathematically oriented keys are used — a public key and a private key. A public key system is designed in such a way that calculation of one key (the 'private key') is computationally infeasible from the other (the 'public key'), even though they are necessarily interrelated. Instead, both keys are produced secretly, as an interrelated pair. In public-key cryptosystems, the public key may be distributed freely, while its paired private key must remain secret. The public key is typically used for encryption, whilst the private key is employed for decryption. RSA is an example of such cryptography. [4]

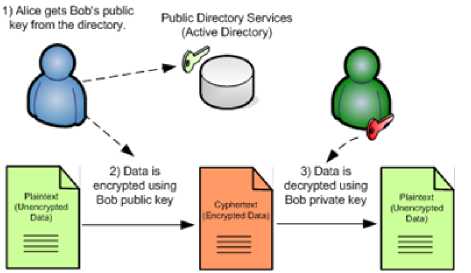
Fig.5. Public-Private Key Cryptosystem

The durability of systems like RSA ( Ron R ivest, Adi S hamir, and Leonard A dleman) lies in the difficulty of the modern computer systems to address the computational intractability of the Integer Factorization problem. RSA is used in most Web browsers and in the SSL protocol. However, to make a system fully secured using RSA, the two prime number needed for the calculation has to be sufficiently large to make it computationally infeasible as far as possible, but still, extremely powerful machines or the advent of quantum computing may challenge this crypto system. Besides repetitive occurrence of a character in a plaintext may sometimes causes some security issues. To tackle such problems, few works have already been done, and one notable schema is the use of different ASCII value from a matrix each time for encryption. ^[11] RSA have also been used to encrypt audio data, and till now not many algorithms are available for developing cryptosystems on audio signal. ^[15]

Visual Cryptography

Visual cryptography is a cryptographic technique which allows visual information such as texts, images etc. to be encrypted in manners by which the decryption can be achieved without using any computers at all, just by using the human visual system if the correct Key image is used. It is an encryption system strongly based upon graphical data and the first introduction of such a cryptosystem appeared in 1994 through the work of Naor and Adi Shamir. Visual cryptography uses two transparent images, often known as Shares; one image contains random pixels while the other contains the clandestine information. It is not at all possible to retrieve the secret information from one of the images. Both transparent images and layers (shares) are required to get the encrypted information. The shares are superimposed on each other to reveal the desired information [10]. But Visual Cryptography often suffers with the problem of Pixel Alignment [14].

Fig.6. Example of Visual Cryptography.

Modern Concerns

Developments such as cloud computing have also shown its potential in mobile world, and as mobile devices have storage limitations, the concept of cloud computing has also been attached to such devices. But privacy of client’s data, stored on the cloud, often comes under scrutiny. Research has been going on in this field for developing new techniques and cryptosystems, as well as enhancing and modifying the existing one, such as encryption using a hybrid cryptosystem, comprising of Advanced Encryption Standard (AES), Schnorr signature and Blake2b before it can be stored in the cloud . ^[12]

Further, advancements such as quantum cryptography, where the counter intuitive behaviour of particles such as photons, known as “Uncertainty Principle”, is being deployed to develop even more robust cryptosystems. [13]

• III.    T he P roposed S ystem

The system discussed here will have multiple features to make things secure as much as possible. All the steps have been outlined below in short, and from there on we will go in some details:

• 1.    Steps of Encryption

• A)    Get the required plaintext from a source.

• B)    Convert character by character to the respective ASCII values, and then to corresponding HEX values.

• C)    Convert each of these values to 8 bit binary digits.

• D)    Now we replace each of the 1s with a randomly chosen one digit Odd integer and 0s with a single digit randomly chosen Even integer.

• E)    We now calculate the final length of the morphed plaintext, chose a random number less than the length, add it up by 100 and make sure it ends up as an odd value. Let us say the value has been put in a variable named z .

• F)    After which we will continue the processing of data- by reversing the string starting from character number z to the end; let’s put the reversed string in a variable named strRev .

• G)    We now concatenate strRev to the rest of the original string, but bring the reversed portion ( strRev ) before the remaining portion of the original text. That remaining portion, starting from character number 1 to z-1 , is not reversed. Let us assume we have put the processed string in a variable named proStr .

• H)    We will now step into the final processing of the ciphertext proStr , by inserting random single-digit values within proStr in positions determined by each of the digits from z . It will be repeated till the end of proStr is reached. This completes series of steps which will produce the final ciphertext.

• 2.    Preparing the Image Key

The image key works like a symmetric key (shared between the sender and receiver), except that there is no avenue for manual entry of any code from keyboard, rather, the receiver selects the obtained image, clicks once on each of the colours, and initiates the decryption process. The procedure will be illustrated further after we unravel the algorithm behind the key and its advantage. The algorithm works in the following way:

• A)    Once the encryption completes, the user will supply two (2) sets of Red (R), Green (G), Blue (B) values (RGB) and (R1G1B1), the values has to be within the range of 1-255.

• B)    The corresponding CalculateRGB() function now prepares Two separate integers from the chosen colour values (by putting the values side by side and choosing random values NOT in excess of the given value for each of R, G and B) and keeps on calculating the difference of these two values till the difference equals z (from section III.1.E ).

• C)    Once we have got our two desired values, the user who encrypts the data, has the job of preparing a Bitmap image, (can be easily done from Microsoft Paint). The image will have two separate colours in it, corresponding to the two values calculated in the CalculateRGB() function, and it will supplied to the receiver as the key to the data from decryption. The image should NOT be converted to JPEG or any other format as decolouring can occur which will change the underlying RGB values.

• 3.    Steps of Decryption

At this stage the encryption has been completed and the required Image key will be generated by following the procedure. One of the major reasons of using such a form symmetric key is the fact that almost all the key’s composed of numbers, letters or special characters, are susceptible to Brute Force and Dictionary attack. These two schemes, given enough time and computational power, will eventually end up finding the key and will be able to automatically check against the encrypted code. In the proposed system, finding two appropriate numbers having difference equal to z, manually creating an image with those values for decryption and finally manual clicking on each of the two different colours before the decryption process can begin, is a series of tasks that is quite a complicated job to come through in an automatic manner for those attacks based on Dictionary and Brute Force algorithms. We will see the whole process of both encryption and decryption with images in a later section. Now we will have an overview of the decryption process step by step.

• A)    Manually select the image key into the image box.

• B)    Click once on each of the two different colours.

With each of the clicks the value required to calculate the difference equal to z (from section III.1.E ) is automatically gleaned from the underlying RGB values; these are stored in two different variables, let us say L1 and L2 .

• C)    Now select the encrypted data source and start the decryption process. Let us consider we put the data in a variable called cryptoData .

• D)    Next difference of L1 and L2 is calculated, for the accurate decryption, this must equal z . Let us say we put this difference in a variable called x .

• E)    Now previously inserted random single-digit values within this encrypted data in positions determined by each of the digits from x will be removed. It will be repeated till the end of cryptoData is reached. Note that if the value of x is not that of z , wrong data bits will be removed the decrypted text will just be a set of random gibberish.

• F)    Following these steps, we will have to reverse back the portion of data (to bring it into original orientation) that have been reversed during encryption.

• G)    The portion of data that have been reversed back in previous step is now concatenated with the rest of the non-reversed portion and position of both these segment are swapped to address the processing in section III.1.G ).

• H)    Going forward, all the even digits will be replaced by a ‘1’ and off digits by a ‘0’.

• I)    Finally, decimal values are determined from this stream of 1’s and 0’s, and ASCII values are mapped from the decimal outputs, revealing the bona-fide information that had been encrypted. This completes the decryption process.

As we can see, an accurate decryption can only be possible if an image with the correct RGB values are supplied as the key.

• IV.    A nalysis of the P rototype D eveloped

As mentioned previously, a prototype has been developed in Visual Basic 6.0 for the demonstration of the algorithm and the general flow of the complete system. Here we will analyse and benchmark the performance and algorithm of each of the core segments mentioned in previous section.

Sample VB code for Encryption and Performance Evaluation

• A)    The algorithm mentioned in section III.1.B to

  • III.1. E can be achieved using the following function:

Private Function LongToBinary$(ByVal lon gv alue&)

Dim hexstring$, digitnum%, digitvalue%, nibblestring$, result string$, factor%, bit% hex string = Hex$(longvalue)

he x s tring = Right$(String$(8, "0") &he xs tring, 8)

For digi tn um = 8 To 1 Step -1

digi tv alue = CLng("&H" & Mid$(he xs tring, digi tn um, 1)) factor = 1

For bit = 3 To 0 Step -1

End If factor = factor * 2

Next digi tn um

LongToBinary = resul ts tring

End Function

Each of the Hex values are first extended to 8 bits from their 4-bit dimension and then usual processing is carried through, the colouring of the line indicates the following summary:

• B)    The algorithm mentioned in section III.1.B to III.1.E can be achieved using the following function:

Private Function BintoDec$(bin$)

Dim s() As String,

ReDim s(1 To Len(bin))

For I = 1 To UBound(s)

s(I) = Mid$(bin, I, 1)

Ifs(I) = "1" Then

s(I) = CStr(RandomInteger(True))

Else

s(I) = CStr(RandomInteger(False))

End If

Next

For I = 1 To UBound(s)

numstr = numstr + s(I)

Next

Randomize z = Int(((Len(numstr)) * Rnd) + 100)

z = IIf(z Mod 2 <> 0, z, z + 1)

numstr1 = StrReverse(Mid(numstr, z))

Dim a() As String sString = CStr(z)

Dim v% v = 1

For I = 1 To Len(numstr1)

CStr(Int((9) * Rnd))

Ifv = Len(sString) - 1 Then v = 1

Else v = v + 1

End If

Next I

BintoDec = numstr2

End Function

The function BintoDec() runs through a set of data having 7,953 characters. The variable z has a global scope and the function also uses another function called RandomInteger(), depicted as follows:

Private Function RandomInteger%(sign As Boolean)

Randomize

Dim z%

Ifsign = True Then

Do z = Int((10) * Rnd)

Loop While (z Mod 2) <> 0

RandomInteger = z

Else

Do z = Int((10) * Rnd)

Loop While (z Mod 2) = 0

RandomInteger = z

End If

End Function

• C)    The algorithm mentioned to devise the two numbers for the preparation of the Image Key in section III.2.A and III.2.B can be attained using the following procedure:

Private Sub CalculateRGB()

Dim s$, r$, g$, b$, r1$, g1$, b1$

Dim tAs Long s = InputBox("Enter RGB Values, each ofthe values mustbe between 0-255",

"", "R=13 G=130 B=130 R1=130 G1=30 B1=130")

Do UntilAbs(t) = z

Randomize r = CStr(Int(Trim(Mid(s, InStr(1, s, "R=") + 2, 3))

• *    Rnd))

g = CStr(Int(Trim(Mid(s, InStr(1, s, "G=") + 2, 3))

• *    Rnd))

b = CStr(Int(Trim(Mid(s, InStr(1, s, "B=") + 2, 3))

• *    Rnd))

r1 = CStr(Int(Trim(Mid(s, InStr(1, s, "R1=") + 3, 3))

• *    Rnd))

g1 = CStr(Int(Trim(Mid(s, InStr(1, s, "G1=") + 3, 3))

• *    Rnd))

b1 = CStr(Int(Trim(Mid(s, InStr(1, s, "B1=") + 3, 3))

• *    Rnd))

Loop

• & " " &b1, , "RGB Sets"

End Sub

The procedure shown above works by accepting two sets of RGB values from the user, and then looping through the possible combinations.

Suppose z equals 28050, therefore possible RGB sets could be {(2 54 32), (53 4 82)} because (25432 – 53482) _Absolute = 28050; or we may have {(34 90 83), (37 7 133)} because (349083 – 377133) Absolute = 28050 as well. The algorithm will keep on evaluating possible combinations of RGB that satisfies the above condition and will show the values soon it finds one.

Now we can just use a simple software such as MS paint to create the Image Key with these sets of values as shown below:

Fig.7. First Pair of Colours (34, 90 and 83)

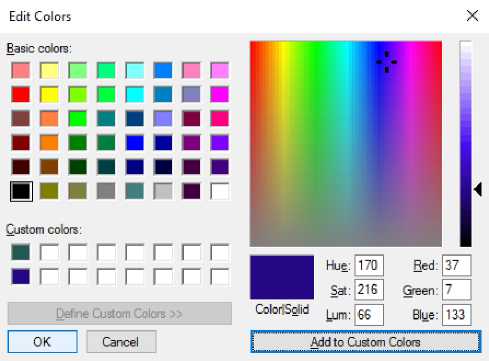
Fig.8. Second Pair of Colours (37, 7 and 133)

And the final Image Key is an image that has both of these colours and is sent with the encrypted code as an uncompressed Bitmap file.

Fig.9. The Final Multi-Colour Image Key

Sample VB code for Decryption and Performance Evaluation

• A)    Now before anything, the user has to load the Image Key in an appropriate Picture Box, and must click once on each of the colours. With each Click,  the following routine calculates the

underlying RGB values and saves the combination in global variables named L1 and L2 ; c is also global.

Private Sub Picturebo x MouseDown(Button As Integer,

ShiftAs Integer, XAs Single, YAs Single)

Dim PixelColor As Long

Dim ColorRedAs Byte, ColorGreen As Byte, ColorBlue As Byte

ColorRed = PixelColor And 255

ColorGreen = (PixelColor\ 256) And 255 ColorBlue = (PixelColor\ 65536) And 255 c = c + 1 Ifc = 1 Then

ColorBlue)

Else

ColorBlue)

End If

Ifc = 2 Then c = 0

End If

End Sub

• B)    The following function takes care of the actual decryption process and it is assumed that L1 and L2 already has the numeric values to begin decryption. Note that wrong values in either of L1 or L2 will render incorrect decryption of the encrypted data. The algorithm has been stated in section III.3.B to III.3.H.

Public Function Decrypt$()

Dim txt3$

Dim txt$

Dim txt1$

Dim sString$

Open lbl.Caption For InputAs #1

txt3 = Input(LOF(1), 1)

Close #1

txt3 = Replace(txt3, vbCrLf, "")

Dim s() As String,

Dim txt2$ sString = CStr(Abs(L1 - L2))

Dim v% v = 1

For I = 1 To Len(txt3)

If(I = CInt(Mid(sString, v, 1)) + 1) Then

End If

Ifv = Len(sString) - 1 Then v = 1

Else v = v + 1

End If

Next I txt = Trim$(txt)

txt1 = StrReverse(Mid(txt, 1, (Len(txt) -

CLng(sString))))

txt2 = Mid( txt, (Len(txt1)) + 2) & "0" & txt1

ReDim s(1 To Len(txt2))

For I = 1 To UBound(s)

IfVal((Mid$(txt2, I, 1))) Mod 2 = 0 Then

s(I) = "1"

Else

s(I) = "0"

End If

Next numstr = vbNullString

For I = 1 To UBound(s)

numstr = numstr + s(I)

Next

Decrypt = numstr

End Function

To finalize the process, as mentioned in section III.3.I, decimal values are derived from the binary stream returned by the above function, and subsequently ASCII values are determined  from the decimal outputs, unveiling the desired information that had been encrypted.

• V.    C onclusion and F uture A spirations

The paper proposed a system where the encryption has been achieved after multiple treatment of the data and a different but effective kind of Key is used encrypt the data. This Image Key and the overall process have been designed in such a way so that the traditional codebreaking systems are either render useless or at least face considerable obstacle in breaking the proposed system in any automatic manner. The algorithms used have all been tested and measured; but needless to say that a lot of performance improvements can be achieved if we can take the code closer to the machine. The system takes some elements out of different cipher systems discussed in Section II, but also adorns and enhances it with completely novel way of taking things forward. One of the cardinal issue that we hope will be address in coming days is the length of the numbers used to generate the Image Key. The lengths of each of the keys should be embedded into the ciphertext itself while encrypting so that the attacker cannot just keep one of the variables ( L1 or L2 ) constant and manipulate the others in some automatic way. These lengths will be checked while decryption and will in fact be used within the decryption logic itself. We can also put more additional logic in the selection of these numbers to make things even more rigorous. It is aspired that more complete and effective systems will be devised in days forward taking the core logic and idea from this paper.

• VI.    T esting and R esult

The Testing section will include encryption and decryption of reasonable large block of characters and the results have been shown using images for an easy and intuitive demonstration. Note the RGB values shown will keep on altering with every run.

Screenshots of Encryption Module of the Developed Prototype

• A)    The initial screen for encryption is shown below, with required data source, having 7,953 characters, has been selected. Pressing Encrypt button initiates the encryption.

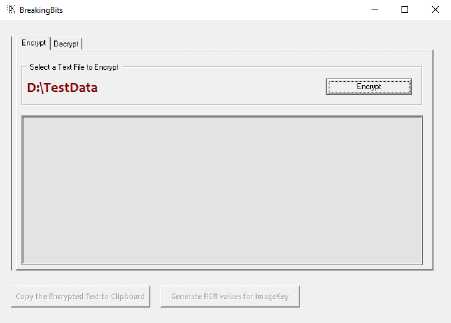
Fig.10. Encryption Screen with Loaded Data Source

• B)    Encryption has been completed as shown in the following screen, with encrypted data available in the Rich Text Box.

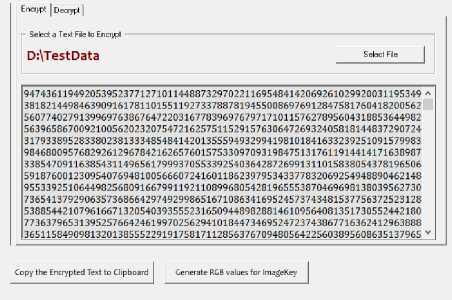
Fig.11. Encrypted Data

• C)    Now Two (2) sets of RGB values are derived as shown below to prepare. … the Image Key.

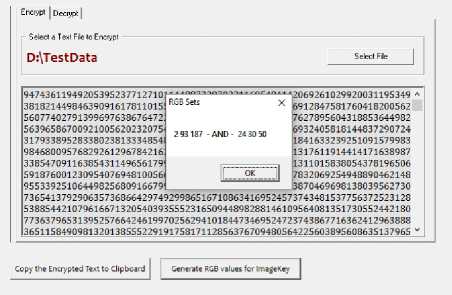
Fig.12. RGB Sets

Screenshots of Decryption Module of the Developed Prototype

A) Screen below showing an appropriate Image Key is loaded and the data source is selected. Now by pressing the Decrypt button (after decryption the caption has changed to “Select File”), decryption has been completed.

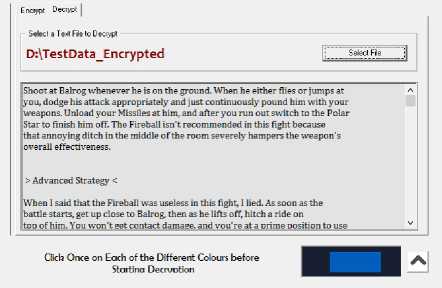
Fig.13. Decrypted Information

The prototype has been developed in a Windows 10 machine with Visual Basic 6.0. The rapid nature of the development environment has been the key factor for its selection as the development platform. The performance analysis have been carried out using VB Watch 2.