Multi Resolution Analysis for Consonant Classification in Noisy Environments

• I.    Introduction

  Speech recognition research has a history of more than 50 years. With the advancement of powerful computers and robust algorithms, Automatic Speech Recognition (ASR) has undergone a great amount of progress over the last few years. For reasons ranging from technological curiosity about the mechanisms for mechanical realization of human speech capabilities, to the desire to automate simple tasks naturally requiring human-machine interactions, research in ASR and speech synthesis by machine has attracted a great deal of attention over the past six decades. The earliest attempt to build an ASR system where made in 1950s’ based on acoustics phonetics features. These systems relied on spectral measurements using spectrum analysis and pattern matching to make recognition decisions on tasks such as vowel recognition [1]. Filter bank analysis was also implemented in some systems to provide spectral information. Several basic speech recognition ideas were emerged in the 1960 s’. Zero – Crossing Analysis (ZCA), speech segmentation, dynamic time aligning and tracking etc algorithms were proposed during this period [2]. In the 1970’s, speech recognition research achieved major milestones. Isolated word recognition systems become possible using Dynamic Time warping (DTW). Linear Predictive Coding (LPC) was extended from speech coding into speech recognition systems based on

  LPC spectral parameters. IBM came out with the effort of large vocabulary speech recognition system in the 70s’, which turned out to be highly successful and had a great impact on speech recognition research. AT & T Bell Labs also began to making truly speaker independent speech recognition systems by studying clustering algorithms for creating speaker independent patterns. In the 1980’s connected word recognition system were devised based on algorithms that concatenated isolated words for recognition. Hidden Markov Models (HMM) are widely used in almost all researchers after mid-1980s. In the late 1980s, Neural Networks were also introduced to problems in speech recognition as a signal classification technique.

There have been a lots of popular attempts carried out towards ASR which kept the research in this area vibrant. Generally a speech recognition system tries to identify the basic unit in any language, phonemes or words which can be compiled into text [3]. The potential applications of ASR include computer speech to text dictation, automatic call routing and machine language translation. ASR is a multi disciplinary area that draws theoretical knowledge from mathematics, physics and engineering. Specific topics include signal processing, information theory, random processes, machine learning, pattern recognition, psychoacoustics and linguistics.

The present research work is motivated by the knowledge that only little attempts were rendered for the automatic speech recognition of CV speech unit in Indian languages like Hindi, Tamil, Bengali, Marathi Chinese etc and very less works have been found to be reported in the literature on the recognition of CV speech units in Malayalam, which is the principal language of South Indian state of Kerala. Very few research attempts were reported so far in the area of Malayalam vowel recognition. So more basic research works are essential in the area of Malayalam CV speech unit recognition.

Malayalam is one of the major languages from Dravidian language family and other major languages include Kannada, Tamil, Telugu, Tulu and Konkani. Malayalam is the principal language of the South Indian state of Kerala and also of the Lakshadweep Islands off the west coast of India spoken by about 36 million people [4]. Malayalam language now contains 51 V/CV units that include 15 short and long vowel sounds and the remaining 36 basic consonant sounds. The earlier writing style of the Malayalam is now substituted with a new style from 1981. Compared to Malayalam and all other Indian languages Tamil seems to be different in the sense that Tamil doesn’t have aspirated sounds and thus the pronunciation is different from other Dravidian language structures. Tamil contains only ‘kharam ’ and ‘anunasikam’ sounds and thus the script used to represent ‘mridu’ sounds are using ‘kharam’. In Tamil the pronunciation of ‘kharam’ lies in the range between ‘kharam’ and ‘mridu’ compared to Malayalam. For example the word ‘ganapathi’ pronounced and scripted as ‘kanapathi’. In Bengali the pronunciation of the vowel ‘a’ is replaced with ‘au’. Due to lineage of Malayalam to both Sanskrit and Tamil, Malayalam language structure has the largest number of phonemic utterances among the Indian languages. Malayalam script includes letters capable of representing all the phoneme of Sanskrit and all Dravidian languages. A unique property of Malayalam is ‘chillukal’ which is derived from the basic consonant units.

A consonant can be defined as a unit sound in spoken language which is described by a constriction or closure at one or more points along the vocal tract. According to Peter Ladefoged, consonants are just ways of beginning or ending of vowels [5]. Consonants are made by restricting or blocking the airflow in some way and each consonant can be distinguished by where this restriction is made [6]. The point of maximum restriction is called the place of articulation of a consonant. A consonant also can be distinguished by how the restriction is made. For example, where there is a complete stoppage of air or only a partial blockage of it. This feature is called the manner of articulation of a consonant. The combination of place and manner of articulation is sufficient to uniquely identify a consonant. In the present work, all the experiments are carried out using 36 Malayalam CV speech unit database uttered by 96 different speakers. For the recognition experiments, database is divided into five different phonetic classes based on the manner of articulation of the consonants as given in table 1.

Table 1: Malayalam CV unit classes

Class	Sounds
Unaspirated	/ka/, /ga/, /cha/, /ja/, /ta/, /da/, /tha/, /d h a/, /pa/,/ba/
Aspirated	/kha/,/gha/,/chcha/,/jha/, /tta/, /dda/, /ththa/, /dha/,/pha/, /bha/
Nasals	/nga/,/na/,/nna/,/na/,/ma/
Approximants	/ya/,/zha/,/va/,/lha/,/la/
Fricatives	/sha/,/shsha/,/sa/,/ha/,/ra/,/rha/

Since human speech is highly dynamic in nature, in order to achieve a reliable representation of the speech signal in the time – frequency plane a multi resolution approach is needed. Wavelet Transform (WT) is a tool for Multi Resolution Analysis (MRA) which can be used to efficiently represent the speech signal in the time – frequency plane. There have been lots of works reported in the literature using WT for the feature extraction process [7][8][9].The objective of the present work is to model Malayalam CV speech unit waveforms using WT based Normalized Wavelet Hybrid Feature (NWHF) extraction technique in speaker independent environments. Classifications are carried out using Artificial Neural Networks (ANN) and k – Nearest Neighborhood (k-NN) algorithms. The performance of the present method is discussed in noisy environments. The rest of the paper is organized as follows. Section II of this paper gives an overview on wavelets and wavelet transform and in section II.1 a brief description on subband coding and multi resolution analysis. Section III.1 and III.2 describes the wavelet decomposition approaches namely Classical Wavelet Decomposition (CWD) and Wavelet Packet Decomposition (WPD) respectively. In section IV, NWHF based feature extraction technique for the Malayalam CV speech unit is explained. Section V.1 and V.2 describes classification using k – NN and ANN classifiers. Section VI presents the simulation experiments conducted using Malayalam CV speech unit database and reports the recognition results obtained using ANN and k – NN classifiers. Finally section VII gives the conclusion and direction for future work.

• II.    WAVELETS AND WAVELET TRANSFORM

Certain ideas of wavelet theory appeared quite a long time ago [10]. Over the last decades wavelet analysis has turned to be a standard technique in the areas of geophysics, meteorology, audio signal processing and image compression [11][12][13]. Wavelet transform can be defined as the transformation of the signal under analysis into another representation which presents the signal in a more useful form [14]. Mathematically a wavelet can be denoted as

• 1     ( t - b ^

Va, b (t) = ^^1      I                              (1)

via  V a >

Where b is the location parameter (translation) and a is the scaling parameter (dilation). Wavelet functions are excellent mathematical tool in the time – frequency analysis of both one dimensional and two dimensional signals. Various important classes of wavelets include smooth wavelets, compactly supported wavelets, symmetric and non – symmetric wavelets, orthogonal and bi orthogonal wavelets etc. Based on the definition of wavelet, wavelet transform of a signal f(t) can be mathematically represented as to

^W ( a , b ) = J ^{f (} t ) V a , b dt                                       ⁽²⁾

-to

TO ie. Wa, b) = J f (t H1V f —b 1                (3)

t =-to       Vi a I V a )

Wavelet transforms are proved to be a very important and useful tool for signal and image processing [14]. Several applications of wavelet transform are already proposed in the literature [15]  [16]. Coifman and

Maggioni had proposed wavelets based on diffusion operators in their work [17]. Hammond et al introduced wavelets on graph via spectral graph theory [18]. Kadambe has made a study on pitch detection algorithm for speech signal using wavelet transform [19]. O Farook et al had proposed in their research work the use of wavelet based feature extraction technique for Hindi phoneme recognition and proved that the proposed technique achieves a better performance over MFCC based features [20].

The Discrete Wavelet Transform (DWT) has been treated as a Natural Wavelet Transform (NWT) for discrete time signals by different authors [21][22]. For computing the wavelet coefficients several discrete algorithms have been established [23]. Daubechies and some others had invented DWT peculiarly designed for analyzing finite set of observations over the set of scales using dyadic discretization [24][25]. As Daubechies mentioned in his work, DWT can be interpreted as continuous wavelets with discrete scale and translation factors. The WT is then evaluated at discrete scale and translation. The discrete scaling is expressed as a=a 0 ^j where i is an integer and a 0 >1. The discrete translation factor is expresses as b=kb 0 a 0 ^j where k is an integer. Thus DWT can be mathematically represented as

DWT;, = CWT {f (t); a = aj,b = kWal j, k e z} j,k                                   0             0 0

where z is the set of integers.

Most often DWT coefficients are usually sampled from CWT on a dyadic grid, i.e., a 0 = 2 and b 0 = 1.

Then wavelet in eqn (1) can be written as

• V» (t) = 2-j/2^(2-j( t - k))

and eqn(3) becomes

W,k (t) = ZS f (k )2 ”‘!1V(2” ‘‘ — k) j k

More effective implementation of DWT is

(5) obtained

using MRA based subband coding technique discussed below.

• A. Multi Resolution Analysis and Subband Coding

Multi Resolution Analysis (MRA) is an effective tool for interpreting the information content of a signal. A MR representation produces a simple hierarchical model to develop the algorithms for the time-frequency analysis of the signal. At different resolution, the details of the speech signal generally characterize vocal characteristics of the speech signal. Each signal to be characterized is analyzed at a coarse resolution and then gradually increases the resolution. Thus MRA can be defined as a technique that permits us to analyze the signal in multiple frequency bands. Two important existing approaches for MRA are the Laplacian Pyramid and Subband coding. To compute the signal details at different resolution Burt and Crowley have introduced the pyramidal implementation [26][27]. In this method the details at different resolutions are regrouped into a pyramidal structure called Laplacian Pyramid. In Laplacian Pyramidal data structures, data at different levels are correlated and this might be a difficulty. Distinctive form Laplacian Pyramid, Subband Coding is an efficient Multi Resolution Spectral Analysis tool for speech signal processing. The main objective of subband coding is to segment the speech signal spectrum into independent subbands in order to treat the subbands individually for different purposes [28].

• III.    WAVELET DECOMPOSITIONS

The main advantage of DWT over FT is the multi resolution analysis of signals with localization on both time and frequency. In the present work we utilize these characteristics of wavelet transform using two major wavelet decomposition techniques for CV speech unit recognition., viz CWD and WPD.

• A.    Classical Wavelet Decomposition (CWD)

In Classical Wavelet Decomposition (CWD), the decomposition of the signal is obtained by successive high pass and low pass filtering of the time domain signal. The original signal is first passed through a halfband highpass filter and a lowpass filter . This is the first level decomposition. This decomposition halves the time resolution since only half the number of samples now characterizes the entire signal. At every level, the filtering and subsampling will result in half the number of samples (and hence half the time resolutions) and half the frequency band spanned (and hence doubles the frequency resolutions). In first level decomposition the speech signal is split into an approximation and detail signal according to high pass and low pass filtering. The approximation is then again split into a second level approximation and detail signal and the process is continued for nth level. CWD based approximation signal Plot of fifth level decomposition for the speech sound /ka/ is plotted in figure 1.

Original signal

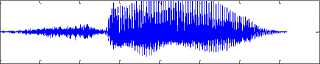
0     500    1000   1500   2000   2500   3000   3500   4000

-1

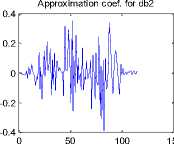
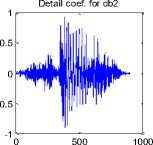
Figure 1: CWD plot for the sound /ka/ using db2

• B.    Wavelet Packet Decomposition (WPD)

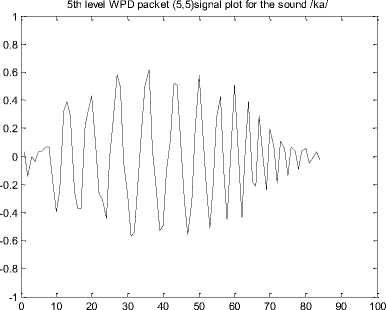
Wavelet Packet Decomposition (WPD) is also known as Wavelet Packets (WP) is a wavelet transform in which the signal is passed through more number of filters than CWD. In CWD, each level is calculated by passing the previous approximation signal through a high pass and low pass filters while is WPD, both approximation and detailed signals are decomposed. WPD Plot for the fifth level of decomposition for the speech sound /ka/ is given in figure 2.

Original signal

-1

0      500     1000     1500    2000    2500    3000    3500

5th level WPD packet (5,5)coefficients for the sound /ka/

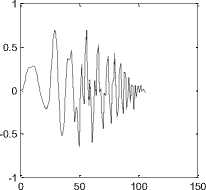
Figure 2: WPD plot for sound /ka/ using db2

• IV.    NORMALIZED WAVELET HYBRID FEATURE EXTRACTION

Normalized Wavelet Hybrid Feature (NWHF) vector for the present work is generated using CWD and WPD method. The process for extracting NWHF feature vector is described below.

In the first step, the sound signal is made to undergo recursively to decompose into kth level of resolutions; depending upon the approximation coefficient matrix at this kth level is sufficient to classify each speech sound to the corresponding sound class and carries enough information content to describe sound characteristics.

Let A k represents this approximation matrix at decomposition level k, which can be written as

A1,1

A A

2,12,2

^A 1, n

^A 2, n

....

^Ak ,1

A         A k,2    .... k,

Then, the first component of NWHF feature vector v1 is, v = 0 0 (A,!

i =1 j =1

In the second step, for Wavelet Packet Decomposition, decompose each speech segment using kth level of resolutions for the best level of wavelet packet decomposition tree. The first coefficient matrix at the best level tree contains enough information to represent the given input consonant CV speech unit without loss of much speech features. Let m represent mean of one row vector in the coefficient matrix then the WPD feature vector v2 is given by v2 = mi, i = 1,2,

.m

(where ‘m’ is the number of rows in the best level coefficient matrix).

In the third step we combined v 1 and v 2 to fusion CWD and WPD coefficients.

V = j{ v} i=1

Then the final feature vector F after z-score normalization is given as

F V - ^(V) ^(V)

Where μ and σ represents mean and variances with respect to the feature vector V

The feature vector of size 20 is estimated by concatenating CWD and WPD features for hybrid feature vectors. The NWHF vector for different speaker shows the identity of the same sound so that an efficient feature vector can be formed using NWHF vectors. The feature vector obtained for different speech unit seems to be distinguishable, giving discriminate feature vector for speech unit recognition.

• V.    CLASSIFICATION

Pattern recognition can be defined as the categorization of input data into identifiable classes via significant feature extraction of the data from the background of irrelevant details. This is the field concerned with machine recognition of meaningful regularities in noisy or complex environments [29]. Nowadays pattern recognition is an integral part of most intelligent systems built for decision making. In the present study two widely used approaches for pattern recognition problems namely statistical pattern classifier (k – NN ) and connectionist approaches (ANN) are used. The task of a classifier component proper of a full system is to use the feature vector provided by the feature extractor to assign the object to a category [30].

• A.    k – Nearest Neighborhood

Pattern classification using distance function is an earliest concept in pattern recognition [31] [32]. Here the proximity of an unknown pattern to a class serves as a measure of its classifications. k – NN is a well known non – parametric classifier, where a posteriori probability is estimated from the frequency of the nearest neighbors of the unknown pattern [33]. For classifying each incoming pattern k – NN requires an appropriate value of k. A newly introduced pattern is then classified to the group where the majority of k nearest neighbor belongs [34]. Hand proposed an effective trial and error approach for identifying the value of k that incurs highest recognition accuracy [35]. Various pattern recognition studies with highest performance accuracy are also reported based on these classification techniques [36] [37] [38].

Consider the cases of m classes ci, i = 1,2,…….m, and a set of N samples pattern yi, i = 1,2,…..N whose classification is priory known. Let x denote an arbitrary incoming pattern. The nearest neighbor classification approach classifies x in the pattern class of its nearest neighbor in the set yi

• i .e. If || x - y _v|| = min|| x - y_t ||², where 1< i < N then x in c j

This is 1 – NN rule since it employs only one nearest neighbor to x for classification. This can be extended by considering k – Nearest Neighbors to x and using a majority – rule type classifier.

• B.    Artificial Neural Network

In recent years, neural networks have been successfully applied in many of the pattern recognition and machine learning systems [39] [40] [41]. ANN is an arbitrary connection of simple computational elements [42]. In other words, ANN’s are massively parallel interconnection of simple neurons which are intended to abstract and model some functionalities of human nervous system [43][44]. Neural networks are designed to mimic the human brain in order to emulate the human performance and there by function intelligently [45]. Neural network models are specified by the network topologies, node or computational element characteristics, and training or learning rules. The three well known standard topologies are single or multilayer perceptrons, Hopfield or recurrent networks and Kohonen or self organizing networks.

Various Neural Network (NN) learning algorithms have been evolved in the past years. In all these algorithms, a set of rules defines the evolution process undertaken by the synaptic connections of the networks, thus allowing them to learn how to perform the specified tasks. In the present study Back Propagation Learning Algorithm (BPLA) is used for classifying Consonant – Vowel (CV) units.

The BPLA is the most popular method for NN training and it has been used to solve numerous real life problems. In a Feed Forward Multi Layer Perceptron (FFMLP), BP algorithm performs iterative minimization of a cost function by making weight connection adjustments according to the error between the computed and desired output values. For the training process a set of feature vectors corresponding to each pattern class is used. Each training pattern consists of a pair of input and the corresponding target output. The patterns are given to the network consecutively, in an iterative manner. The appropriate weight corrections are made during training to adjust the network to the desired behavior. The iteration continues until the weight values allow the network to perform the required mapping. Each iteration of whole pattern set is named as an epoch.

Present work investigates the recognition capabilities of the FFMLP based Malayalam consonant recognition system using Multi Layer Feed Forward Neural Network (MLFFNN) and BP algorithm. The number of nodes in the input layer is fixed to 20 according to NWHF vector size. The number of nodes in the output layer is 36 for 36 Malayalam CV units. The experiment is repeated by changing the number of hidden layers. After trial and error experiments the number of hidden layer is fixed as 8 and the number of epochs as 10,000 for obtaining the successful architecture in the present study.

The simulation experiments and the results obtained using these two pattern recognition (ANN and k – NN ) approaches are presented in the next section.

• VI.    SIMULATION EXPERIMENT AND RESULTS

0.5

In order to investigate the use of wavelet based CV speech unit feature enhancement and to compare with different speech modeling algorithms explained in section V with respect to their simulation experimental results in various noise levels, we carry out all of the above techniques in a noisy as well as clean speech recognition experiment and is summarized in the following para.

36 Malayalam basic consonant units from the speaker independent Malayalam CV speech unit corpus are used as the speech database for the present speech recognition task. Each CV speech signal lowpass filtered to 4 kHz and sampled at 8 kHz sampling rate and quantized to 16 bits is used in this study. The database consists of the utterances from 96 different native Malayalam speaking male and female young speakers. The dataset is then divided into training and testing set which contains first 48 samples for training and the remaining 48 samples for testing. Thus training and testing set contains a total of 1728 samples each. The main objective of this article is to design a robust CV speech unit recognizer in additive noisy condition. To perform this task each speech signal is corrupted by adding Additive White Gaussian Noise (AWGN) of different Signal to Noise (SNR) levels.

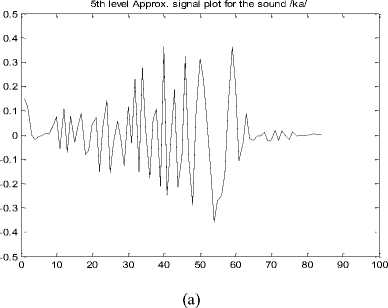
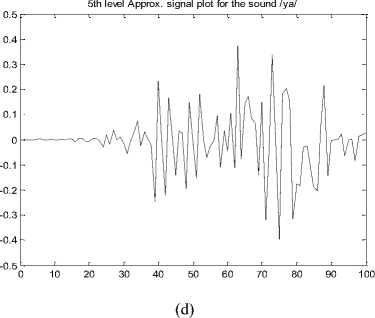
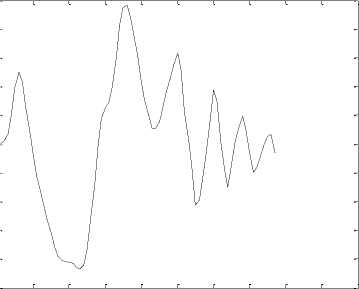
As explained in section III.1 an example of CWD based approximation signal plot is given in figure 3 (a – e) . This represents 5th level decomposition signal plot for the Malayalam CV speech databases of 5 different phonetic classes aspirated, unaspirated, nasals, approximants and fricatives.

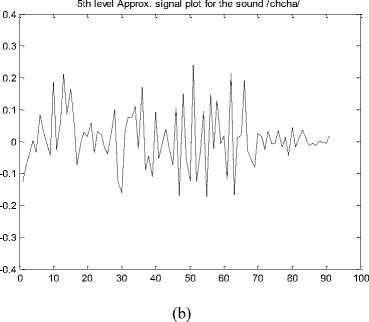
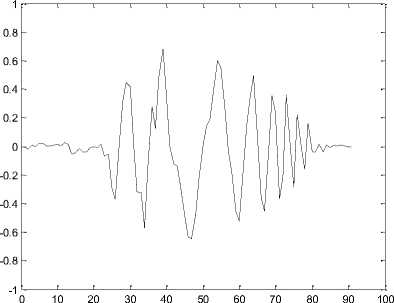
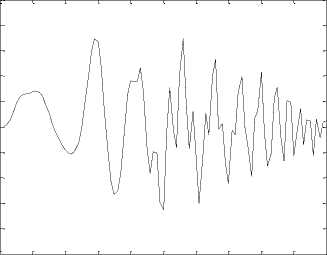
Section III.2 describes WPD coefficients for each CV speech sound for hybrid features. An example of WPD signal plot for 5 different phonetic classes are given in figure 4.

-0.5 0

5th level Approx. signal plot for the sound /nga/

0.4

0.3

0.2

0.1

-0.1

-0.2

-0.3

-0.4

10    20    30    40    50    60    70    80    90    100

(a)

(c)

5th level Approx. signal plot for the sound /ya/

5th level WPD packet (5,5)signal plot for the sound /chcha/

(b)

5th level WPD packet (5,5)signal plot for the sound /nga/

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

0    10    20    30    40    50    60    70    80    90    100

-1

(c )

0    10    20    30    40    50    60    70    80    90    100

(e)

Figure 3. CWD based approximation signal plot for (a) Unaspirated, (b) Aspirated, (c) Nasals, (d) Approximants and (e) Fricatives

5th level WPD packet (5,5)signal plot for the sound /ya/

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

0    10    20    30    40    50    60    70    80    90    100

(d)

5th level WPD packet (5,5)signal plot for the sound /sha/

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

0     10    20    30    40    50    60    70    80    90    100

(e)

Considerable variation on these plots illustrates the difference in sound classes or groups under consideration for classification. Hence the NWHF feature vectors can effectively be used as a discriminate parameter for the classification purpose. Classification experiments are done using ANN and k – NN classifier. The simulation experiments are repeated using 5 different mother wavelets namely haar, symlets, coiflets, db2 and db4. It is found that Daubechies wavelet db2 is optimum for the classification of Malayalam CV speech unit database. Experimental results using 5 different wavelet families for clean speech using k – NN and ANN are tabulated in Table 2 and Table 3 respectively.

The recognition accuracies obtained for Malayalam CV speech database for the five different phonetic classes at various SNR levels using db2 are tabulated in Table 4 and Table5.

Figure 4. WPD signal plot for (a) Unaspirated, (b) Aspirated, (c) Nasals, (d) Approximants and (e) Fricatives

Table 2: Recognition Accuracies for 5 different mother wavelets using NWHF vector and k – NN.

Class	haar	symlets	Coiflets	db2	db4
Unaspirated	34.2	44.2	51.3	62.6	60.2
Aspirated	36.1	45.9	50.5	63.3	60.9
Nasals	37.8	43.8	49.3	65.7	62.4
Approximants	35.3	46.9	52.9	64.9	61.5
Fricatives	36.9	47.2	54.8	63.5	60.2

Table 3: Recognition Accuracies for 5 different mother wavelet using NWHF vector and ANN.

Class	haar	symlets	Coiflets	db2	db4
Unaspirated	45.9	54.8	62.3	71.8	70.1
Aspirated	46.8	55.2	60.7	73.9	70.9
Nasals	47.2	53.2	59.3	79.7	64.4
Approximants	45.9	56.9	63.2	74.9	61.4
Fricatives	46.1	57.9	64.6	76.4	63.7

Table4. Recognition Accuracies of 5 different phonetic classes using NWHF and k – NN for different SNR values.

Class	0 dB	3 dB	10 dB	20 dB	30 dB	40 dB	Clean
Unaspirated	25.7	28.9	45.5	56.2	62.4	62.6	62.6
Aspirated	29.1	36.4	47.9	59.6	63.9	63.4	63.3
Nasals	46.1	50.9	57.6	61.2	65.7	65.7	65.7
Approximants	41.7	48.3	55.2	60.6	64.8	64.8	64.9
Fricatives	43.3	49.1	56.5	60.9	63.1	63.6	63.5

Table5 Recognition Accuracies of 5 different phonetic classes using NWHF and ANN for different SNR values.

Class	0 dB	3 dB	10 dB	20 dB	30 dB	40 dB	Clean
Unaspirated	34.7	40.6	51.5	67.8	71.2	71.8	71.8
Aspirated	36.9	42.7	54.8	70.2	73.8	73.9	73.9
Nasals	44.1	51.3	58.7	74.8	79.9	79.6	79.7
Approximants	40.4	46.9	55.4	71.6	74.5	74.9	74.9
Fricatives	42.5	50.2	57.3	73.6	76.1	76.2	76.4

• VII.    CONCLUSION

A Multi Resolution Analysis (MRA) approach to Malayalam Consonant – Vowel (CV) speech unit recognition using Wavelet Transform (WT) has been studied. Two decomposition algorithms namely Classical Wavelet Decomposition (CWD) and Wavelet Packet Decomposition are combined to extract Normalized Wavelet Hybrid Feature (NWHF) vector for the present classification study. Daubecheis wavelet db2 is found as optimum mother wavelet in the present work. The recognition accuracies are calculated and compared using Artificial Neural Network (ANN) and k – Nearest Neighborhood (k – NN) at different levels of Signal to Noise Ratio (SNR) values and it is observed that the NWHF parameters improve their recognition accuracies by increasing SNR levels. Recognition of Malayalam CV speech unit with large database and effective implementation of wavelet features in combination with frequency domain features would be some of our future research directions.