Мультифрактальное моделирование для контроля качества и оценки механических свойств стеклопластиковых труб

Актуальность исследования обусловлена возрастающими требованиями к повышению надежности и эксплуатационного ресурса композитных труб [1], что открывает новые возможности для создания легких, долговечных и энергоэффективных конструкций [2]. Композитные трубы обладают рядом характеристик, включая высокую прочность, трещиностойкость и коррозионную стойкость, что делает их конкурентоспособной альтернативой стальным аналогам [3].

Трубы сохраняют стабильность в процессе эксплуатации, в том числе при воздействии высоких температур [4]. Однако производительность композитов может варьироваться в зависимости от количества слоев и дисперсии волокон [5], а также типа армирующих материалов, например, базальтового волокна [6]. Поэтому усиление физико-механических свойств композитных труб остается одной из ключевых задач [7].

Одним из решений этой проблемы является разработка математических моделей [8], которые позволяют прогнозировать качество труб на основе их состава [9], структуры [10] и условий эксплуатации [11]. Для установления взаимосвязи между структурой материала и его свойствами предлагается использовать теорию фракталов [12], [13]. Применение методов, основанных на теории фракталов открывает возможности не только для эффективного прогнозирования и корректировки свойств/характеристик труб в процессе производства, но и для рационализации их состава, что, в свою очередь, существенно повысит эксплуатационные характеристики и продлит срок службы композитных труб.

Потребность в разработке методов управления свойствами композитных труб [14] становится все более актуальной в связи с растущими требованиями к функциональности и экономической эффективности конструкций [15]. Теория фракталов, основанная на концепции дробной размерности, предоставляет мощный инструмент для описания и анализа сложных, неоднородных систем, таких как композиционные материалы [16].

Применение фрактального анализа в различных областях науки демонстрирует его эффективность в решении широкого круга задач. Фрактальные методы успешно применяются для оценки сложных систем [17], ранжировании критериев качества периодических технологий [18], прогнозирования свойств материалов для атомной энергетики [19] и различных материалов для строительных конструкций [19], бетонов различного состава [20], стали [21], а также для исследования проницаемости горных пород [22], механических свойств сланцев [23], ударной прочности композитов [24], влиянии поверхности углеродных нанотрубок на свойства полимерных нанокомпозитов [25], диэлектрических свойств полимерных композитов [26], исследовании и применение в материалах гражданского строительства [27], оценке поведения усадки при высыхании грунтовых композитов [28] и даже для оптимизации теплообмена в фотоэлектрических системах [29] и т.д.

Большинство существующих работ фокусируются на общих характеристиках композитов без детального изучения влияния микроструктуры на их свойства.

Объектом исследования являются стеклопластиковые композитные трубы, а предметом — микроструктура этих труб и ее связь с механическими свойствами. Целью исследования является Разработка и верификация метода оценки и прогнозирования механических свойств стеклопластиковых труб на основе мультифрактального анализа микроструктуры.

Задачи исследования:

• 1.    Провести экспериментальные исследования механических свойств стеклопластиковых композитных труб.

• 2.    Выполнить мультифрактальный анализ микроструктуры труб для оценки спектра мультифрактальных размерностей.

• 3.    Установить количественные связи между мультифрактальными параметрами и механическими свойствами с помощью статистического моделирования.

• 4.    Разработать математические модели для прогнозирования механических свойств на основе микроструктурных данных.

• 2    Materials and Methods

Исследуемые образцы: стеклопластиковые трубы с внутренним диаметром ~70 мм (Рис. 1).

Рис. 1 - Общий вид сегмента трубы

Fig. 1 - General view of a pipe segment

Из стеклопластиковой трубы изготавливались образцы для механических испытаний в виде прямоугольной формы с габаритными размерами ~280×10 мм (l×bg) (Рис. 2). Образцы вырезались с применением ленточной пилы.

A-A(2:1)

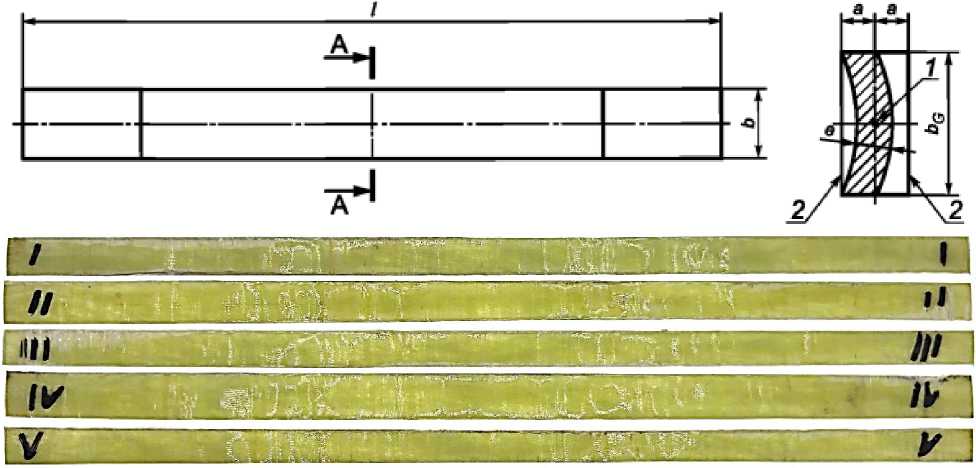
Рис. 2 - Внешний вид образцов для испытаний

Fig. 2 - Appearance of test samples

Исследования включали оценку внешнего вида изделия, проведение механических испытаний на растяжение с последующим изучением зоны разрушения образцов. Механические испытания проводились на разрывной машине при скорости движения траверсы 2 мм/мин.

Результаты механических испытаний на прочность, упругость и пластичность приведены в Таблице 1.

Таблица 1. Механические свойства стеклопластиковых труб

Table 1. Mechanical properties of fiberglass pipes

Образец, №	Осевая прочность, МПа	Модуль упругости, ГПа	Относительное удлинение, %
1	205	10.0	3.0
2	218	10.5	2.0
3	204	9.7	3.0
4	186	9.0	3.5
5	219	11.0	2.0

Микроструктура исследовалась с применением растровой электронной микроскопии.

• 3    Results and Discussion

В процессе испытаний образцов труб на растяжение, при напряжении в ~40 МПа и до момента разрушения, были слышимы регулярные щелчки, сопровождающиеся незначительным снижением напряжения и соответствующем образованием «зубьев» на графике «напряжение-время» (Рисунок 3, №1). С приближением к осевой прочности материала труб частота щелчков снижалась (Рисунок 3, №2).

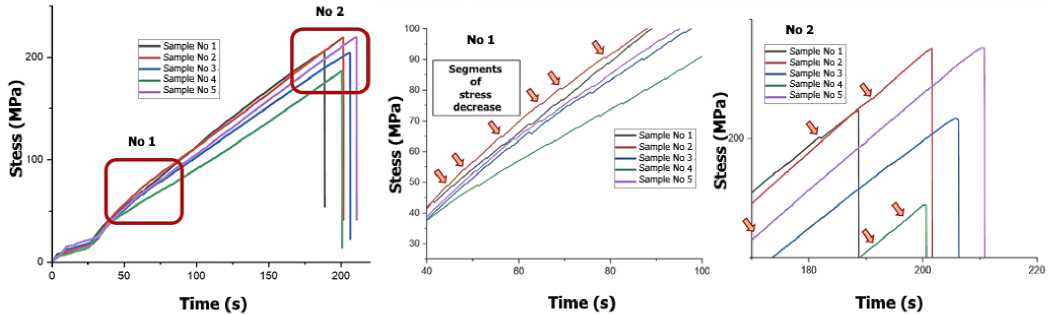
Рис. 3 - Скачкообразные падения напряжения в процессе растяжения

Fig. 3 - Jumpy stress drops during stretching

Формирование «зуба» связано с образованием поперечной трещины на поверхности, которая распространялась, вероятно, до следующего слоя (Рисунок 4). Являясь концентратором напряжений, по достижению критического напряжения, трещина начинала расти в продольном направлении, приводя сначала к расслоению, а затем разрушению внутренних армирующих слоёв (Рисунок 5).

Рис. 4 - Поперечные трещины в рабочей зоне

Fig. 4 - Transverse cracks in the working area

Рис. 5 - Зона разрушения образца

Fig. 5 - Sample destruction zone

В изделии присутствовали остаточные напряжения, приводившие к видимому загибанию

отрезанных образцов во внешнюю сторону (Рисунок 6).

Рис. 6 - Изгиб готового образца для испытаний

Fig. 6 - Bending of the finished test specimen

Матрица обладает частичной светопропускаемостью (Рисунок 2.14). При просвечивании образцов различались видимые области внутренних слоёв, которые в том числе могли являться областями с меньшей межслойной адгезией (Рисунок 2.15).

Рис. 7 - Оценка светопроницаемости изделия просвечиванием образца

Fig. 7 - Evaluation of the light transmittance of a product by shining a sample through the light

Рис. 8 - Границы засвеченного внутреннего слоя в образце

Fig. 8 - Boundaries of the illuminated inner layer in the sample

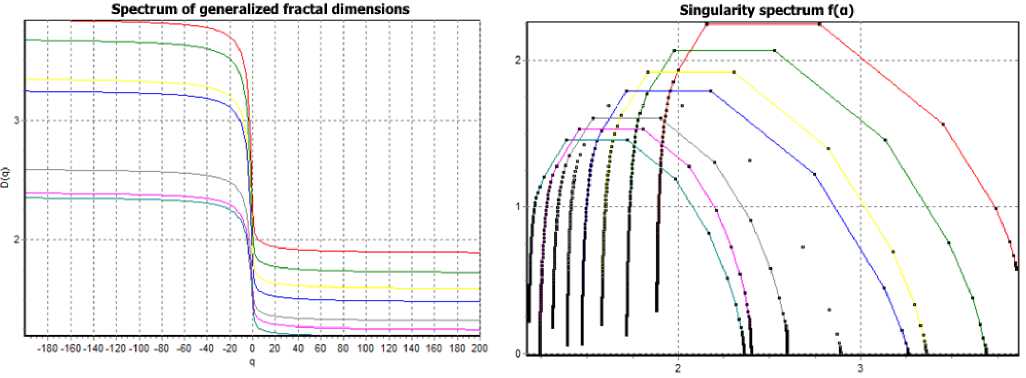
Спектр мультифрактальных размерностей микроструктуры рассчитывался на основании анализа спектра размерностей Реньи (1) [30], [31] и показан на Рисунке 9.

D ( q ) =

1       ln ∑ ^N p i^q

⋅ lim     ^{i = 1}

q - 1 δ→∞ lnδ где δ - линейный размер ячейки квадратной сетки, которой следует покрывать неоднородный объект только для вычисления его размерности, pi - вероятность попадания точки, которая находится на исследуемом объекте, в i-ю ячейку сетки с

N размером δ , ∑ p_i ^q i = 1

– обобщенная

статистическая сумма, которая характеризуется показателем степени q, который принимает любые значения в диапазоне от -∞ до +∞ , в данном случае показатель q изменялся в диапазоне значений от -200 до 200.

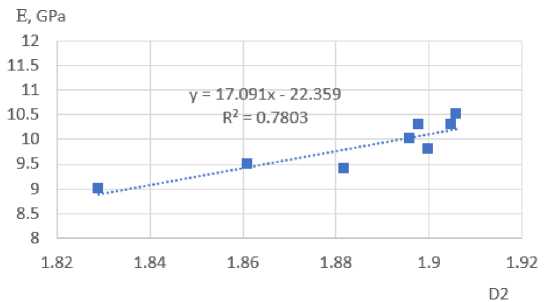
Соотношения между мультифрактальными размерностями микроструктуры и механическими свойствами приведены на Рис. 9. Повышение фрактальной размерности D 0 и корреляционной размерности D 2 волокон (ровинга) приводит к возрастанию показателей предела прочности на осевое растяжение σ p на 15% и модуля упругости E на 14%, что обусловлено повышением компактности заполнения пространства волокнами матрицы стеклопластиковых труб. При снижении показателей информационной размерности D 1 значения пластичности (относительного удлинения δ ) возросли ∼ 30%.

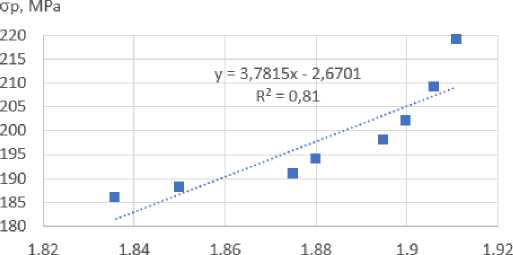
а

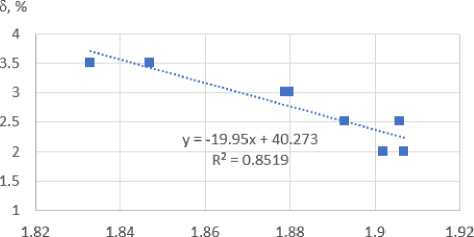
b

c

Рис. 9 - Зависимости между прочностью на растяжение (а), относительным сужением (b), модулем упругости (с) и мультифрактальными размерностями стеклопластика

Fig. 9 - Relationships between tensile strength (a), relative contraction (b), elastic modulus (c) and multifractal dimensions of fiberglass

Спектр получали путем преобразований Лежандра функции для каждой структурной составляющей каждого отдельно взятого фотоснимка микроструктуры (2). По результатам анализа канонического спектра рассчитаны показатели неоднородности функции f ( a ) при q = 200 . Если структура полностью однородна, то спектр f ( a ) вырождается в точку.

dT а = ~Г, dq                                                 (2)

, ^f ( а ) = q a - т ( q )

Возрастание неоднородности волокон стеклопластика в 3D пространстве свидетельствует о том, что поверхность менее гладкой. Неоднородность структуры стеклопластиковых труб означает неравномерное распределение точек по областям, на которые разбивается структура, то есть ее геометрически одинаковые элементы заполнены точками с различной вероятностью. При этом показатели прочности труб возрастают, и показатели модуля упругости тоже. Уменьшение показателей неоднородности свидетельствует о возрастании отклонений графиков функций от нуля. Если структура полностью однородна, то спектр f ( a ) вырождается в точку.

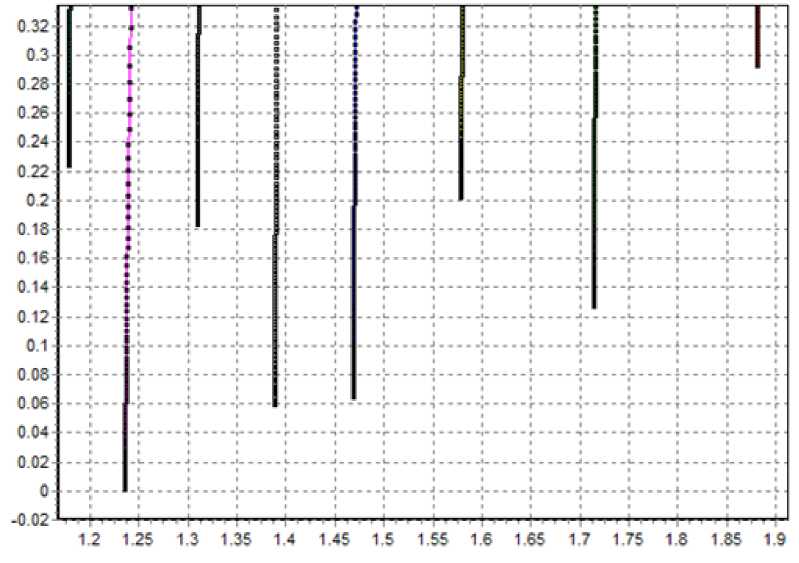
На рис. 10 b, c приведены графики распределения неоднородности стеклопластиковых труб.

a

b

Singularity spectrum f(a)

с

Рис. 10 - Спектр мультифрактальных размерностей D(q) волокон матрицы стеклопластиковых труб (a), канонический спектр f(a) (b) и увеличенный фрагмент спектра f(a) (c), где отклонение значений функций от нуля свидетельствует об неоднородности исследуемой структуры

Fig. 10 - Spectrum of multifractal dimensions D(q) of fiberglass pipe matrix fibers (a), canonical spectrum f(a) (b) and enlarged fragment of spectrum f(a) (c), where deviation of function values from zero indicates heterogeneity of the structure under study

Численные значения коэффициентов парной корреляции математических моделей прогноза свойств из Рис. 9 изменяются в пределах от 0.78 до 0.85, что свидетельствует об удовлетворительной согласованности результатов и об их возможности применять данный подход для первичного анализа критериев качества труб как после заводской поставки, так и для оценки технического их состояния труб при первичном осмотре.

• 4    Conclusions

• 1.    Разработан метод оценки свойств стеклопластиковых труб на основе мультифрактального анализа. Предложенный метод позволяет количественно оценить неоднородность структуры волокон и установить связь между структурными характеристиками и механическими свойствами материала.

• 2.    Автоматизирован расчет спектра мультифрактальных размерностей Реньи. Разработанный алгоритм позволяет быстро и эффективно обрабатывать экспериментальные данные и получать информацию о структуре материала.

• 3.    Установлена корреляция между мультифрактальными характеристиками и механическими свойствами стеклопластиковых труб. Полученные результаты демонстрируют высокую степень корреляции между спектральными характеристиками и такими показателями, как прочность, удлинение и модуль упругости (коэффициенты корреляции 0.78–0.85).

• 4.    Созданы математические модели для прогнозирования механических свойств труб на основе мультифрактального анализа. Разработанные модели позволяют прогнозировать механические характеристики труб с достаточной точностью, что подтверждается экспериментальными данными.

• 5.    Предложенный метод может быть использован для экспресс-оценки качества стеклопластиковых труб. Благодаря автоматизации расчетов метод может быть эффективно применен для контроля качества продукции на производстве.

• 5 Fundings

  This research was supported by a grant from the Russian Science Foundation No. 24-19-00691, https://rscf.ru/project/24-19-00691/.