Мультифрактальный анализ композиционного материала на основе терморасширенного графита

Для применения фрактального анализа в исследовании структур ТРГ возникает необходимость обоснования того, что ТРГ является фракталом. Фрактал – структура, состоящая из частиц, которые в каком-то смысле подобны целому. Это рекурсивная модель, каждая частица которой структурно повторяет в своем развитии развитие всей модели в целом. В данном случае идентификация, т.е. самоподобие – одно из основных свойств фрактальных структур. Второе важное свойство – изменение характеристик (масса, плотность, площадь поверхности, модуль упругости и т. д.) с изменением размера фрактального объекта или пространственного масштаба, в котором этот объект рассматривают. Для фрактального анализа частиц ТРГ использовался метод островов среза [3]. Компьютерная реализация данного метода осуществлялась в программном пакете MATLAB по следующему алгоритму:

• •    бинаризация изображения (преобразование изображения в черно-белое);

• •    преобразование изображения в негатив (выделение границ частиц);

• •    определение периметра и площади каждой частицы (размерность в пикселях);

• •    преобразование размерности площади и периметра частиц из пикселей в мкм;

• •    графическое изображение полученных данных в логарифмических координатах;

• •    аппроксимация с помощью метода наименьших квадратов полученных данных в виде линейной зависимости;

• •    нахождение фрактальной размерности, как тангенса наклона полученной прямой.

Для исследования фрактальной природы ТРГ использовался измельченный порошок в виде насыпной смеси частиц с общей размерностью <400 мкм. Изображения частиц были получены при помощи оптического микроскопа «Альтами МЕТ 5» при увеличении в 50 раз с использованием проходящего света в светлом поле (рис. 1).

Рис. 1. Изображение частиц ТРГ фракция 100-63. х50

Проведенная обработка по вышеприведенному алгоритму позволила получить линейную зависимость в логарифмических координатах. Анализ полученных результатов позволил установить, что ТРГ является фракталом, и к нему применим аппарат фрактального анализа. Фрактальная размерность D оказалась различной ( в диапазоне 0,890-1,598), причем с уменьшением фракции значение фрактальной размерности увеличивается. На рис. 2 представлена логарифмическая зависимость площади и периметра частиц с размерностью в диапазоне 315-63 мкм.

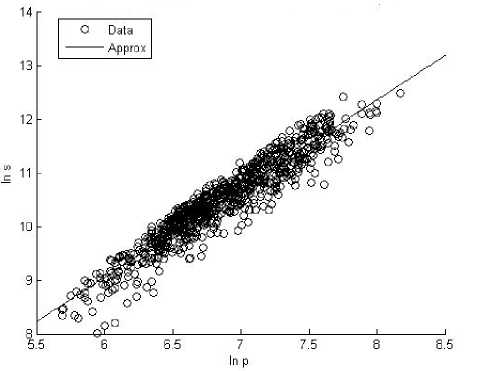
Рис. 2. Линейная зависимость площади и периметра частиц ТРГ для фракций 315-63 мкм

Полученные значения фрактальной размерности позволили установить их взаимосвязь с некоторыми механическими свойствами ТРГ, в частности, с модулем упругости. С этой целью было проведено испытание ряда образцов цилиндрической формы на сжатие. Образцы изготавливались из композита, содержащего частицы ТРГ разных фракций и модифицированную силиконовую смолу. Соотношение частиц ТРГ и модифицированной силиконовой смолы в композите составляло 40/60 масс.%. Образцы подвергались последующей термической обработке при температуре 2000С в течение 30 мин. На рис. 3 представлена зависимость модуля упругости от фрактальной размерности.

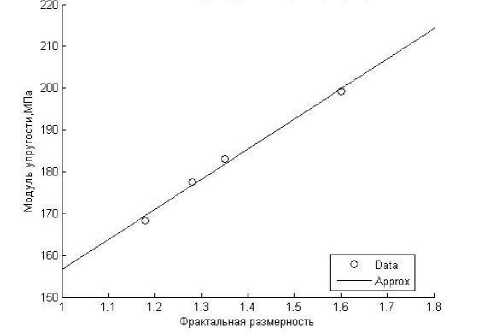
Рис. 3. Зависимость модуля упругости от фрактальной размерности

Для более полного описания неупорядоченных структур требуется определение спектра различных размерностей, т.е. использование мультифрактального формализма [4]. Мультифрактал - неоднородный фрактальный объект, для полного описания которого недостаточно введения одной фрактальной размерности D, а необходим целый спектр таких размерностей. Реализация метода мультифрактальной параметризации проводилась способом покрытия сетками [5], алгоритм получения мультифрактальных характеристик состоит из следующих этапов:

• •    бинаризация изображения изучаемой структуры - преобразование полученного изображения в черно-белое;

• •    разбиение площади изображения на квадратную сетку с ячейками определенного размера;

• •    построение для каждого разбиения вероятности распределения частиц ТРГ в ячейках P i = n iI N, где n i -количество точек в ячейке с номером i ; N - общее количество частиц в матрице крупных ячеек;

• •    оценка обобщенной корреляционной функции:

  
  
  

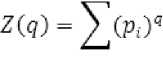
Показатель q может принимать любые значения.

• •    нахождение распределения

1 Z(q)

• •    определение двух характеристик

  
  
  
  

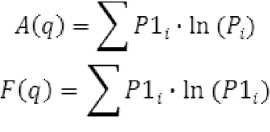
  Рис. 4. Изображение шлифа поверхности композиционного материала на основе ТРГ. (х200)

  
  

• •    построение графика зависимости A(q) и F(q) . По методу наименьших квадратов определяется угол наклона прямых.

  
  
  
  
  
  

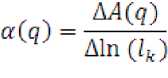
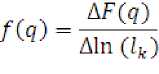
• •    определение т ( q ) и обобщенной фрактальной размерности D q

T^ = q -a-Kq)

D_q = r(q)/(q - 1)

• •    определение упорядоченности:

  ^9 — Dq D_o

  
  
  

  Рис. 5. Бинарное изображение фрагмента поверхности композиционного материала на основе ТРГ

  
  

  Для установления мультифрактального характера ТРГ были изготовлены шлифы образцов, полученных при одноосном прессовании [6]. Соотношение компонентов ТРГ и модифицированной силиконовой смолы 60/40 масс.% соответственно, максимальная нагрузка прессования 43 МПа. Снимок поверхности шлифа был получен на микроскопе «Альтами MET5» при увеличении х200 с размером пикселей 1024 ^х 768 (рис. 4). Для расчетов был взят фрагмент бинаризиро-ванного изображения размером 512 ^х 512 пикселей (рис. 5).

Представленные на рис. 6 данные показывают, что спектр обобщенных фрактальных размерностей D q зависит от степенного показателя q . Если D q меняется в зависимости от q , то рассматриваемое множество точек является мультифракталом. На это также может указывать нелинейность функции τ ( q ) (рис. 7). По характеру полученных функций сделан вывод, что материал на основе ТРГ является мультифракталом.

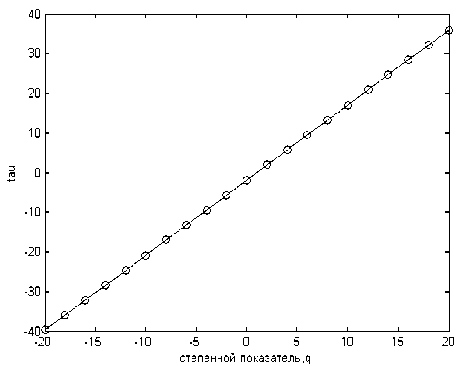
Рис. 6. Зависимость обобщенной фрактальной размерности от степенного показателя q

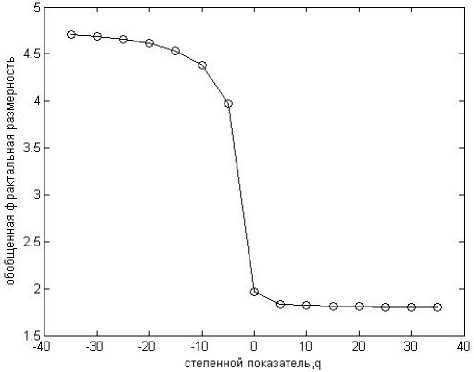
Рис. 7. Зависимость функции т ( q ) от степенного показателя q

Для исследования взаимосвязи механических характеристик ТРГ с мультифрактальными характеристиками использовались два параметра: упорядоченность и однородность структуры. Фракционный состав исследуемого композиционного материала на основе ТРГ составлял 300215 мкм. Образцы цилиндрической формы размером ø12х18 мм получали путем одноосного прессования с последующим спеканием при температуре 180^оС. Микроструктура полученного материала на основе ТРГ и модифицированной силиконовой смолы исследовали с помощью микроскопа «Альтами МЕТ5» и цифровой фотосъемки при диапазонах увеличения х50, х100, х200, х400. Анализ полученных мультифрак-тальных характеристик однородности f q и упорядоченности ∆ q в зависимости от расчетного параметра q позволил выбрать для дальнейшего рассмотрения увеличение в 100 раз.

В качестве изучаемого параметра исследовалась микротвердость поверхности образца. Для определения микротвердости использовался метод царапания (склерометрии) [7]. Измерение твердости методом склерометрии заключается в анализе профиля царапин, нанесенных на поверхность материала. Значение твердости исследуемого материала определяется относительно известного значения твердости стандартного образца по соотношению нагрузок на образец и ширины царапин, полученных на исследуемом и стандартном образцах. Устройство для нанесения царапин позволяет проводить эксперименты на образцах размером 30х30х30 мм со скоростью перемещения индентора 4 мм/мин и нагрузкой 15 Н [7]. В качестве индентора использовалась четырехгранная пирамида, установленная гранью служащей в качестве царапающей кромки. Расчет микротвердости осуществлялся по формуле H=P/b2, где H - микротвердость, P - нагрузка на индентор, b – средняя ширина царапины, мм. Далее для определения микротвердости композиционного материала на основе ТРГ использовались образцы с процентным соотношением связующего вещества равного 20, 40 и 60% от общей массы. Изображения царапины были получены с помощью микроскопа «Альтами МЕТ5» и цифровой фотосъемки при увеличении х100 (рис. 8). Размер царапины определялся с помощью программного обеспечения Almati-Studio. Анализ проведенных исследований показал, что оптимальной нагрузкой является нагрузка в 1,5 Н, поскольку при этом сохраняется линейный характер зависимости между микротвердостью и упорядоченностью структуры (рис. 9).

Рис. 8. Изображения шлифа при 40% концентрации полимера и при нагрузке царапания 1,5 Н

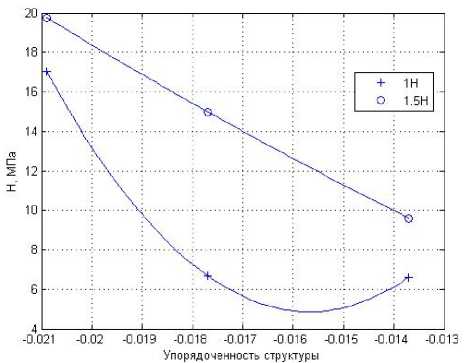
Рис. 9. Ввзаимосвязь микротвердости от упорядоченности структуры для нагрузок 1 Н и 1,5 Н при q =-0,5

Установлено также, что линейная связь характерна и для зависимости концентрации связующего вещества от упорядоченности материала (рис. 10). По диаграмме, представленной на рис. 11, можно установить локализацию экспериментальных точек при меньших концентрациях связующего и небольшой разброс с увеличением связующего материала.

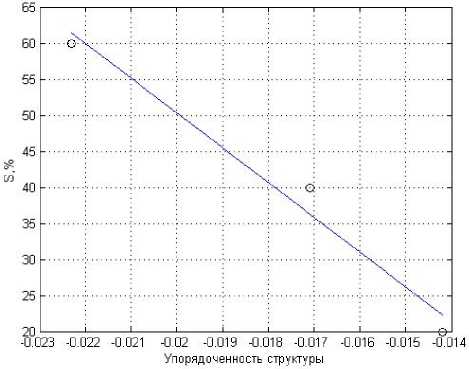
Рис. 10. Взаимосвязь концентрации связующего вещества от упорядоченности структуры при q=-0,5

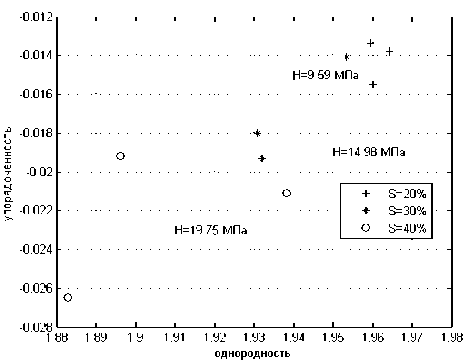
Рис. 11. Диаграмма упорядоченность-однородность для экспериментальных точек при q =-0,5

Выводы:   по упорядоченности и однородности микрошлифов можно определить состав композиционного материала на основе ТРГ и его механические свойства.