Multiple Information Hiding using Cubical Approach on Random Grids

Published Online October 2015 in MECS DOI: 10.5815/ijcnis.2015.11.06

The amount of data being sent over the internet is ever increasing because of the rapid growth of computer network and communication technologies. However, the secret data transmitted over an open channel is prone to interference, forgery or attacks by intruders. Therefore, it is important to conceal the information before it is transmitted. Techniques like cryptography convert intelligible information to unintelligible form to meet the security requirements and services. Steganography is another solution to the problem, but unlike cryptography the presence of the secret information is not revealed. Visual Cryptography scheme that was proposed by Noar and Shamir [2] is a secret sharing scheme which divides the secret information into many shares. For a (k:n) secret sharing scheme, a minimum of k shares are required to reveal the information. The general VSS Schemes encodes a secret message into two shares, which are noisy in nature. By stacking these two shares, the secret message is divulged visually. Using VSS, the secret information can be encoded and shared with participants. The partakers can decode the secret image by collecting the shares from other participants and stacking those shares to recover the secret information. Thus, no complex calculations, computer assistance, or correlated background knowledge is required to recover the information. Also the possession of a single share does not reveal any information about the secret. RGVSS is another type of probabilistic scheme that generates shares without pixel expansion and also does not use a code book as a reference to generate the share. A comparison of VC-based VSS with RG-based VSS shows that the former scheme suffers from pixel expansion problem resulting in an increased size of the encrypted shares thereby generating greater traffic. The encryption is limited to only one secret. Visual Cryptography requires a complex codebook to generate the cipher text.

In recursive hiding of secrets, several additional messages can be hidden in one of the shares of the original secret. The secret images that are to be hidden are taken according to their sizes, from smallest to largest. The size of the secrets increases by a factor of two. This concept provides a means to an efficient exploitation of the excess bits.

The rest of this paper is organized as follows. The related work section is described in Section 2. The extension to deal with proposed methodology and design strategy is given in Section 3 and 4 respectively. The experimental results are demonstrated in Section 5. Section 8 will present conclusions. Finally, future scopes are given in Section 9.

• II.    Related Works

• A.    Random Grids

  Kafri and Keren[1] in 1987, defined random grids as a collection of 2D array of pixels for a binary image. Each pixel can be fully transparent (white) or simply opaque (black). The value for a pixel that is black is depicted as 1 and the transparent pixel takes the value as 0. Random Grids is a fully probabilistic method, with the probability of a pixel being white or black is 50%. The value of a pixel is decided by the coin-flip procedure. If ‘p’ is a pixel in a random grid R, then the probability of ‘r’ being white(transparent) or black(opaque) is given as P(r=0)=P(r=1)= ½ . The size of the random share is more than that of the secret image but there is no pixel expansion or the need for a complex codebook. The average light transmission of the random grid is ½ and is given by the equation below:

hw

A ( R ) =  ---EE a ( r [ i , j ]) h x w~T_v

In equation (1), w x h is the size of the secret image and B[i,j] represents the binary pixel in the secret image corresponding to the cell (i, j). The algorithm used for designing is acquired from [2] which have the highest contrast value of ½. The implementation of the algorithm is given in Figure 1.

The algorithm for implementing random grid offers the highest contrast value of ½.

Algorithm 1: random_grid_algorithm

• 1:    Generate R1 as a random grid

  // for (each pixel R1[i, j ], 1 ≤ i ≤ w and 1 ≤ j ≤ h ) do

  // R1[i, j] = randomly select a pixel

• 2:    for (each pixel B[i, j ], 1 ≤ i ≤ w and 1 ≤ j ≤ h ) do

  • 2.1:    {

if (B[i, j] = 0) R2[i, j] = R1[i, j ] else R2[i, j] = 1 - R1[i, j ]

}

• 3:    output (R1, R2)

By taking practicality into account, many variations of the main VSS scheme have been presented by various authors for encryption of halftone [4, 6, 7, 8, 9, 18], grayscale [15] and colored images [13, 18]. These papers demonstrate that increasing the carrying capacity of secrets affects the contrast and distortion of decrypted secret.

Dhakal

DEEPENDRA

SMIT

(a)

(b)

(c)

(d)

Fig 1. Implementing Algorithm 1: (a) Secret Image (b) Secret share R1 (c) Secret share R2 (d) Recovered secret by XOR operation on R1 and R2 with PSNR value 4.072

• B.    Multiple Information Hiding

The carrying capacity of the grid has always been a limitation of random grids is that we are able to encrypt only a single secret. Chen [6,8] broadened this approach to encrypt multiple secrets, where the secret images can be decrypted by stacking the two shares and then rotating one share while keeping the other share fixed at one position. This scheme has a limitation that a maximum of four secrets can be hidden because of the rectangular shape of the random grids. Assuming that there are four secret images, A, B, C, and D, of size m by m pixels is to be encrypted into two cipher-grids namely R1 and R2 without the problem of any pixel expansion and the secrets could be recovered by directly stacking and then rotating one of the two cipher-grids at 90°, 180° or 270° respectively to decrypt the rest of the secrets. However, increasing the number of secrets leads to the loss of contrast [12]. Since the angles of rotation are known, an attacker may try to decrypt the secrets by using Bruteforce technique if he could get his hand on to both the shares but even then it would be significantly difficult since this smaller random grid shares are embedded into cube shares into several different patterns.

Gurung [14] suggested the idea of using circular representation of the shares to increase the variations on the number of angular rotations (columnar shifts) possible on a given share generated by the RGVSS scheme. One of the shares is used as a basis to hide the other secret information using various circular rotations. The idea combines the concept of segmentation [5] with RGVSS. However the number of shares is increased as the number of secret information increases.

Gurung [18] proposed a VMSS scheme by exploiting the geometrical configuration of a sphere by encrypting multiple secrets into two spherical shares but use of a sphere distorts the image after decryption. Therefore, only text secrets can be encrypted as images become unrecognizable after decryption.

• C.    Recursive Information Hiding

The traditional VC scheme suffers from a few drawbacks as discussed earlier. The most significant among these is the limitation of only being able to encrypt one image. The idea of recursive information hiding overcomes this limitation by allowing one to encrypt multiple images efficiently.

In recursive image hiding technique [3], the images that are to be encrypted are taken in the increasing order of their sizes. First, the shares of the smallest image that is to be encrypted are generated. These randomly generated shares are then concatenated to generate the first share of the second secret image. The second share of the secret image is obtained in such a manner that if the two shares are superimposed on each other, the original image can be obtained. As already pointed out, the images have to be taken in the increasing order of their sizes. The shares of the smallest image are hidden in the shares of the image which is next larger in size and the shares of this image are hidden within the shares of the next larger image. So, in this way the secret information is recursively hidden in the shares of the secret images. Therefore, the original (largest) image has got all the hidden information within its shares. The decryption process is simple. It is the exact reverse of the encryption process. We first need to extract the shares of the original image and from those shares we recursively extract the shares of the smaller images till we obtain the shares of the smallest hidden image [10].

This scheme extends the usability and capacity of the traditional visual cryptography scheme by allowing one to encrypt multiple images. However, it is also subject to a certain restriction. The size of the secret image that is to be hidden within the original image should be a multiple of 2 with respect to the original image’s size. For instance, if the size of the original image is 6 × 6, then the size of the first secret image has to be 3 × 3 and the size of the second secret image will be 6 × 3. The advantage of the scheme is that it ensures that the bits are preserved in subsequent encryption of secrets which ensures 100 % efficiency [11]

Recursive techniques also been used to hide the Most Significant Bits (MSBs) of one secret images to the Least Significant Bits (LSBs) of another. Katta [7] proposed a recursive hiding scheme for 3 out of 5 secret sharing. The idea used is to hide smaller secrets in the shares of a larger secret without an expansion in the size of the latter.

Input: A binary image A of size rows x cols, where B[i,j] ϵ {0,1} (white or black), 1 <  i <  rows and 1 <  j <  cols, image B of size row x col, where B[i,j] ϵ {0,1} (white or black), 1 <  i <  row and 1 <  j <  col. Here, col = cols+cols

Output: Four shares, R1, R2, R3 and R4 are generated which reveal A and B when superimposed, where R_k [i,j] ϵ A, 1 <  i <  rows and 1 <  j <  cols and k ϵ {1,2} and where R_k [i,j] ϵ B, 1 <  i <  row and 1 <  j <  col and k ϵ {3,4}

Algorithm 2: Recursive_Hiding_Algorithm

• 1:    Generate R1 as a random grid

  // for (each pixel R1[i, j ], 1 ≤ i ≤ w and 1 ≤ j ≤ h ) do

  // R1[i, j] = random_pixel(0, 1)

• 2:    for (each pixel A[i, j ], 1 ≤ i ≤ w and 1 ≤ j ≤ h ) do

  • 2.1:    { if (A[i, j] = 0) R2[i, j] = R1[i, j ]

else R2[i, j] = 1 - R1[i, j ]

}

• 3:    Concatenate R1 and R2 to form another grid R3 // for (each pixel R1[i, j ], 1 ≤ i ≤rows and 1 ≤ j ≤ cols ) do R3[i,j]=R1[i,j];

k=j;

// for (each pixel R1[i, j ], 1 ≤ i ≤rows and 1 ≤ j ≤ cols ) do R3[i,k+j]=R2[i,j];

• 4:    Generate R4,

  • 4.1    for (each pixel B[i, j ], 1 ≤ i ≤ row and 1 ≤ j ≤col ) do

    • 4.1.1   {          if (B[i, j] = 0) R4[i, j] = R3[i, j ]

5. output(R3,R4)

else R4[i, j] = 1 – R3[i, j ]

}

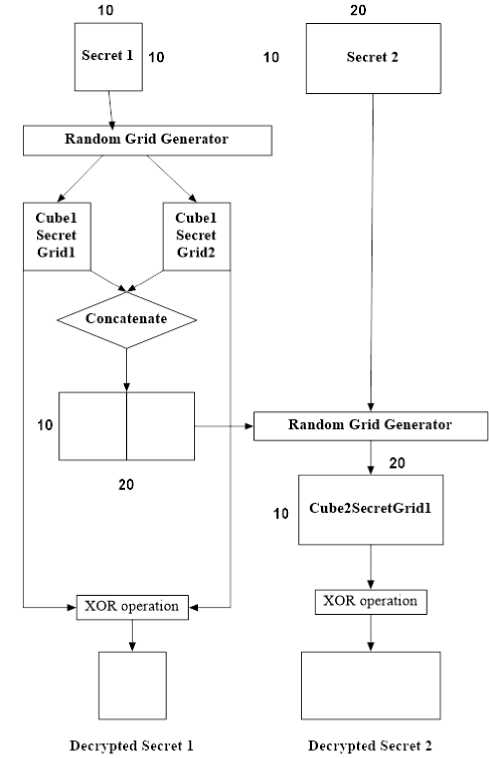
Fig.2. Block diagram of Recursive Image Hiding Technique

• III.    Proposed Methodology

The proposed methodology exploits the notion of random grids and combines it with multiple information hiding and recursive image hiding for generating cubical random grids. Multiple information hiding is done on each face of the cube to enhance the carrying capacity.

For decryption, all the shares are represented as cubes and one cube is stacked over the other. While one cube remains fixed, the sides of the second cube are interchanged and rotated till all the secrets are revealed. There might be multiple secrets on one face, whereas, two faces may combine together to hide a larger secret using recursion. A cube has 6 sides; it is assumed that the cube is spread-out in such a way that each side is attached to at least one adjacent side.

Fig.3. Patterns in Which a Cube Can Be Spread-Out

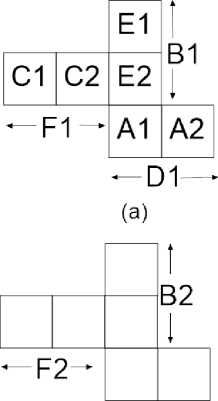
Algorithm 3 takes in ‘4’ images as input and utilizes Algorithm 1 to generate two random cipher grids at various rotations for each of the images taken as input. Hence, a total of two shares are generated. Here, we generate 2 shares for encrypting four secret images. Each of the cypher grids thus formed is considered to be any one of the sides of one of the two cube shares. This means that each side of the cube has the capability of encrypting a maximum of four secrets when Algorithm 3 is followed. The cypher grids R1 and R2 when stacked together reveal the first secret, the rest of the secrets are revealed at various rotations of the cypher grids (refer Figure.4). Recursive hiding of secrets is implemented by concatenating the shares of one image and then using the large share to generate the second share for the second image. In this case, when we incorporate the recursive format onto the cubical topology, one of the cubical shares will have the concatenated shares of the same image i.e. if suppose P having dimension m x m is encrypted into two shares S1 and S2 of the same dimension then, the first cube share will have both S1 and S2 inserted on any two adjacent side of the cube in any one of the cube patterns previously shown in Figure.2. Now, the larger share which takes in two of the sides of the cube will have dimension of 2m x m. This larger share will be the Share 1 for the larger image of size 2m x m. The second share of the secret image is obtained in such a manner that if the two shares are overlaid on top of each other, the original image can be obtained. Hence, the shares of the smallest image are hidden in the shares of the image which is next larger in size and the shares of this image are hidden within the shares of the next larger image. So, in this way the secret information is recursively hidden in the shares of the secret images (Refer to Figure 4).

The cubical approach on random grids lets us increase the carrying capacity by several folds. For the purpose of decryption the shares are represented as cubical shares and then the participating cubical shares are stacked together. For decrypting the hidden image both the shares are made into a cube in the correct pattern in which the secrets are embedded in to rectangular noise like girds.

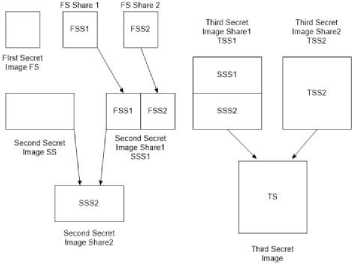
Fig.4. Implementation of Recursive Image Hiding

For decrypting other hidden images both the cube shares are stacked and then keeping one cube fixed, the other cube is rotated at various degrees over the fixed one. The knowledge of the pattern followed is of utmost importance if somebody is to decrypt any of the secrets encrypted in to that noise like grids. The encryption of secrets using various patterns makes it difficult for the hacker to unwrap the information even by Brute-force method.

• IV.    Design Strategy

This section discusses the overall stratagem of approaching the solution i.e. the technique by which encryption and decryption of the information with the secret embedded in it. To implement this scheme for multiple secret hiding, the binary image for the secrets which is generated by using the concept of threshold is fed to the multiple_info_hiding_algo . Figure 5 diagrammatically shows the change of pixel positions at various rotations while encryption of the secret.

Input: Four binary secret images GK={GK(i, j)|GK(i, j)=0 or1(white or black), 0 < i < (m-1), 0 < j < (m-1)} where K=A, B, C and D.

Output: Two cipher-grids RK={RK(i, j)|RK(i, j)=0 or1(white or black), 0 < i < (m-1), 0 < j < (m-1)} where p=1 and 2. R1 and R2 reveals one secret image by directly stacking the two random grids and the other three in an additional way of rotating one RG at 90, 180, or 270 degrees, respectively.

The secret images are then randomly selected and using the pixel information of the randomly selected secret images, the first and second shares are generated as two random grids R1 and R2. The pixel information of all the secret images is now stored in the two shares generated (refer to Algorithm 3). Each of this m x m shares can be represented as a side of each of the two cube shares. So for encrypting secrets on each side of the cube we require two cubic pattern embedded shares. Each of those shares has six sides. Figure 6 shows a block diagram for multiple information hiding in each side if the cube. Now, if each of these six sides has four secrets then we can encrypt N, number of secrets in one cube share, that is,

N= sides of the cubes x secrets embedded on each side

N= 6 x 4

N= 24

Algorithm 3: multiple_info_hiding_algo

• 1:    Generate R1 and R2 as a random grid

  // for (each pixel R1[i, j ], 1 ≤ i ≤ rows and 1 ≤ j ≤ cols) do

  // R1[i, j] = randomly select a pixel

  // for (each pixel R2[i, j ], 1 ≤ i ≤rows and 1 ≤ j ≤ cols) do

  // R2[i, j] = randomly select a pixel

• 2:    Randomly select pixel coordinates for the binary secret images.

  • 2.1:    Randomly select any of the four binary secret images A, B, C or D

• 2.1. a: //at 0 degree

if (selected_image==A)

• {       if (A[i,j]==0) R2[i,j]=R1[i,j];

• 2.1.b: //at 90 degree

Else R2[i,j]=1-R1[i,j];

}

if (selected_image==B)

{       if (B[j,(rows)-i+1]==0)R2[j,(rows)-i+1]=R1[i,j];

else R2[j,(rows)-i+1]=1-R1[i,j];

}

R1(j,(rows)-i+1)= randomly select a pixel

• 2.1. c: //at 270 degree

if (selected_image==C)

• {      if (C[(rows)-j+1,i)==0)

• 2.1.d ://at 180degree

R2[(rows)-j+1,i]=R1[j,(rows)-i+1];

else R2[(rows)-j+1,i]=1-R1[j,(rows)-i+1];

}

R1[(rows)-j+1,i]= randomly select a pixel

if (selected_image==D)

{      if (D[(rows)-i+1,(rows)-j+1]==0)

R2[(rows)-i+1,(rows)-j+1]=R1[(rows)-j+1,i];

else R2[(rows)-i+1,(rows)-j+1]=1-R1[(rows)-j+1,i];

}

R1[(rows)-i+1,(rows)-j+1]= randomly select a pixel

• 3: output(R1,R2)

  

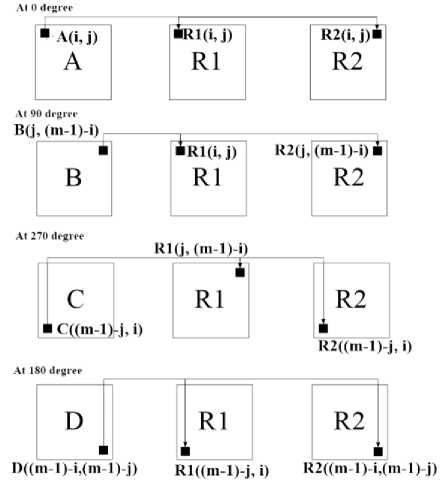
  Fig.5. Diagram of the Processes Followed In the Encryption of Secrets by Rotation of Pixel Position

  
  
  

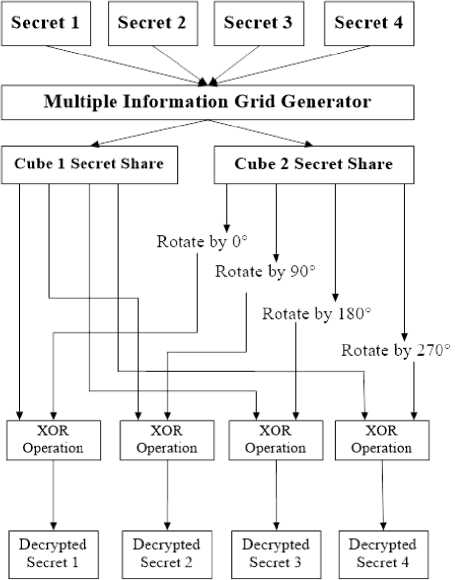
  Fig.6. Block Diagram of Multiple Image Hiding

  
  

It can encrypt as many as 24 secrets could be encrypted and shared by embedding shares on the cubic side patterns. Figure 7.i refers to two cubic shares of the same secrets. The shares generated are extremely noise like and when stacked can never be decrypted unless the pattern in which the secrets are embedded are known and made into cubes. Hence, the property of authentication and security is maintained. It depicts two different patterns in which a cube can be spread-out. Each side of the cube is a share of four secret images embedded on the six sides of the cube. The secrets can be decrypted only when the corresponding sides of the cubes are overlapped. The two cube shares in Fig. 7.i (a) and 7.i (b) are encrypted in different patterns and the shares of the secrets hidden have been jumbled in such a manner that merely overlapping the shares will not reveal any information.

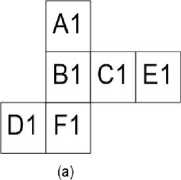
A=A1+A2 B=B1+B2 C=C1+C2 D=D1+D2 E=E1+E2 F=F1*F2

Fig.7(i). Various Design Strategies for Embedding Secrets into Cubic Shares (a) Deploying Algorithm 3 Cubic Share_1 (b) Deploying

Algorithm 3 Cubic Share_2

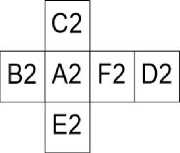
(b)

For anybody to successfully decrypt the entire secret, the pattern in which the secrets are hidden should be known. After the pattern is known, the spread-out shares are put together to form a cube and the secrets are revealed by keeping one cube fixed and rotating the other cube at different axis till one secret is revealed in one of the side of the cube. After the first secret is revealed at one side, the cube is rotated along the same axis at different angles to reveal the other three secrets encrypted in the two overlapped corresponding shares. Once all the four secrets of a certain side of the cube are revealed, the cube is rotated on a different axis and the above procedure is repeated till all the other secrets are revealed. Since one cube has to be fitted inside another cube, hence, the size of one cube should be bigger than the other. There are various combinations for creating a cube as discussed in Figure 3 which shows various patterns in which a single cube share could be made therefore; decryption by third party gets complicated as there can be many ways and combinations in which the two cubical shares are generated which adds to extra security for the information shared.

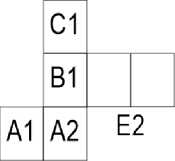
A=A1+A2=D1

B=B1+B2

C=C1+C2

D=D1+D2

F=F1+F2=E1

E=E1+E2

D1

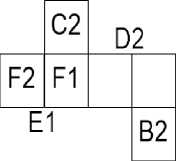
Fig.7(ii). Various Design Strategies for Embedding Secrets into Cubic Shares (c) Deploying Recursive Image Hiding with

Algorithm2Cubic_Recur1_Share1 (d) Deploying Recursive Image Hiding with Algorithm2Cubic_Recur1_Share2

И

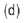
Figure 7.ii depicts another different strategy which shows two cubical shares (c) and (d); in this particular design strategy combination of cubical patterns use of recursive image hiding is done along with Algorithm 3 . Separately each of this cube shares can hold some information as a whole, which means holder of each of the cubical shares will be able to reveal some of the secrets on their own, but only if the patterns in which the secrets were embedded are known to them. In Fig 7.ii: (c) and (d) A1 and A2 are the shares of the same information and so are F2 and F1. So, the holders will have some information individually but for them to reveal all the secrets embedded both the shares will be needed. This could be a very effective way of information distribution where the holders are given some amount of independence but mutual cooperation is also ensured. Security of the information will still be intact as the probability of finding the two exact shares of the same information is very low.

A=A1+A2; F=F1+F2

Both the above discussed strategies requires us to embed secret into a sheet at any of the patterns, carrying capacity is increased by several folds compared to any of the presently available. To reveal all the secrets the sheet can be cut into the pattern in which the secrets were embedded and made out into a cube for easy retrieval by HVS.

• A. Application

The next strategy about to be discussed is a unique secret sharing technique where safe deposit type information sharing scheme can be replicated. In Figure 7, (b) is considered as the master key piece of the safe deposit locker box, when talking in terms of shares as keys. The holder of this particular share will have administrative authority over B1, D1 & F1 since, to reveal B, D & F the holders of B1, D1 & F1 will require 8(b) which acts as the master key for information B, D & F as it is embedded with the shares B2, D2 and F2. Hence the holder of 8(b) can act as the bank manager and B1, D1 & F1 be the clients. In the above figure let us consider 8(b) as the master key piece of the safe deposit locker box, when talking in terms of shares as keys. The holder of this particular share will have administrative authority over B1, D1 & F1 since, to reveal B, D & F the holders of B1, D1 & F1 will require 8(b) which acts as the master key for information B, D & F as it is embedded with the shares B2, D2 and F2. Hence the holder of 8(b) can act as the bank manager and B1, D1 & F1 be the clients. Each of these clients will have some information with themselves (A, E & C). The respective shares of A, E & C are encrypted as any two sides of the first cubical share. In Figure 8 (a), the shares of A (A1 & A2) are given to the same client and partial information about the key is known to the client. The shares in Figure 8(a) are generated using multiple_info_hiding_algo and hence each share holds multiple number of information. This information can be revealed by stacking the two shares and rotating them at various angles. The shares of E & C can also be given to different clients. The corresponding shares of A, E & C combine to form shares B1, F1 and D1 respectively. Here, Recursive hiding technique is used where nearly 100% efficiency is provided as explained in [3]. The drawback of recursive hiding is that the size of a share increases in the ratio 2:1 (refer Figure 9).

(b)

Fig.8. KAK Strategy (a) Client Cubical Share (b) Master Key Share

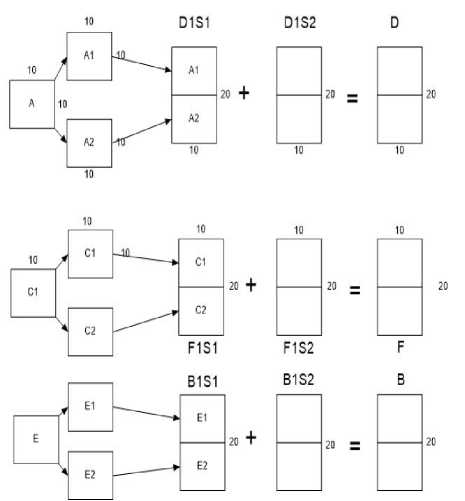
Fig.9. Deploying Recursive Image Hiding Technique on Figure 7

(g)

(i)

(f)

(h)

(j)

In this approach, this drawback has been used as to hide more information. Each larger share can hold more information as the dimensions increases on either its width or length. Depending on how the adjacent sides have been chosen. For example, in figure 8(a), the shares C1 and C2 combine to form a larger share F1. Using F1, the second large share F2 is generated. Similarly, B1 and D1 are formed which are used to generate B2 and D2.The next section of the paper discussed the experimental results of the proposed methodology.

Fig.10. Implementing Algorithm 3 (a) Secret Image A (b) Secret Image B (c) Secret Image C (d) Secret Image D (e) Random Share R1 (f) Random Share R2 (g) Recovered secret by stacking R1 and R2 with PSNR 4.1536 (h) Recovered secret by rotating R2 by 90° with PSNR 4.1569 (i) Recovered secret by rotating R2 by 180° with PSNR 3.9573 (j) Recovered secret by rotating R2 by 270° with PSNR 3.8543

V. Simulation And Experiment

Some experiments are conducted to demonstrate the feasibility and applicability of the proposed scheme. Each of the results after simulation shown below depicts a side of the cubical share when implementing Algorithm 1 and Algorithm 3, although Figure 12 depicts a 3D model of the same. The messages on four secret images A, B, C and D are of size of 512 x 512 are simple English alphabets shown in Figure 10 (a–d).

SG КРС

(a)                    (b)

АР КР

(c)                      (d)

They are encrypted into two cipher-grids R1 and R2 with the size of 512 x 512, shown in Figure 10(e) and f).The first secret image A is decrypted by stacking R1 with R2 directly as shown in Figure 10(g). Upon rotating R2 right at 90° the second secret image B is decrypted by stacking R1 and the rotated R2 which can be recognized visually as shown in Figure 10(h). Upon rotating R2 at 180°, the third secret image C is decrypted by stacking R1 and the rotated R2 and recognized visually as shown in Figure 10(i). Rotating R2 clockwise at 270°, the fourth secret image D is decrypted by stacking R1 and the rotated R2 and recognized visually as shown in Figure 10(j).

Contrast of the reconstructed result by stacking two cipher-grids of one of the sides of a cubical share, in which Algorithm 3 is implemented where, one grid is rotated by 0, 90, 180, and 270 degrees, respectively, over the other cipher-grid is always greater than zero[10]. By the proposed scheme the recovered secret has a 1/4^th area to disclose a single secret say, S remaining 3/4^th of the area is independent of the secret S. Contrast depends on the average light transmission of a cypher grid. The average light transmission of 2 stacked random grids is:

mm 22

L[Ri [ ^ о ]] = L[R ^le2 ] = —SS I ₂1 = ₂ m _х m k = k = <  2 )  2.

mm

L [ Rj [ ^ 1 ]] = —m SS ( ⁰ ) = ⁰

m x — k = ² k = ²

The average light transmission of stacking R1 and R2

1     3      113 15

l [ R [ S_to Л =- L[R [ S ] + ³ L[R [ S , Л - - x-+ ³ x - - -( 0 )       4       ¹   ( 0 )      4       ^{1    ( 1 )}       4   2   4   4   -6

And, the cube in its patterns embedding secrets on each side of the cubical share is large.

Peak Signal to Noise Ratio (PSNR) value of the input image and the secret image that is revealed at the end using the formula:

1     3     13 13

L ^{[ R [} 5 ( 1 ) ^]] = 4 L^[R i ^[S ( 1 ) ^]] + 4 L^[ j S ( 1 ) ^]] = 4 ^x о + 4 ^x 4 = ₁₆

To estimate the visual quality of the reconstructed image R for secret image S, the contrast is defined as

MSE —

w * h

w - 1 h - 1                            ²

EH i ( i , j ) - к ( . , j ) ]

1 - 0 j - 0

The PSNR is defined as:

,   ,   L [ R [ S (0) ]] - L [ R [ S ₀) ]]

contrast —-----—---------^J—

1 + L [ R [ S _0>]]

PSNR — 10.log₁₀

Г MAX 2 ( MSE

20.log10

MAX, ^ . V MSE J

The contrast comparison of the strategies discussed is depicted in Table 2. Two shares of the four secret images contain different pixel information of the respective secrets. A single share contains (1 m ) pixel information for hiding m secrets and without overlapping has an average light transmission of 12 . The overlapped share thus has ( m — 1 m > pixels of information and after overlapping the share’s average light transmission is 14 . Therefore, the average light transmission of white pixels of the two cypher grids for m secret images can be given as;

•

( m —1)

m

PSNR — 20. log ₀ ( MAX, ) - 10. log; ₀ ( MSE )

Here, MAX i is the maximum possible pixel value of the image. When the pixels are represented using 8 bits per sample, this is 255. For Binary image it is 1. The PSNR of the three secret images is given in Figure 1, 10 and 11 and the comparison of PSNR has been given in Table 1 for multiple information hiding of four secrets into two shares.

(a)

Similarly, the average light pixels can be given as;

transmission of black

L [ S 1] - 0 • - + ¹

m 4

L [ S 1] = ( m - ¹⁾ 4 m

( m - 1)

m

Sikkim Manipal University

Arindam Parmar

Kshitij Panghaal

Kritartha Paul ChoudhuryG 1

Sandeep Gurung

(b)

Hence, the contrast of the decrypted information can be generalized as;

contrast —

( m + 1)    ( m - 1)

4 m 4 m

^{( m - 1)}

^{1 +} 4 m

2 contrast —-----

5 m - 1

Security of the proposed VSS scheme by random grids for binary images is secure, i.e., each cipher-grid, or alone reveals no information of the secret images unless the dimension or the pattern in which the random grids are embedded into the cubical share is known. Hence, even if both the cubical shares get leaked, the security of the secrets remains intact and authentication is satisfied. The mathematical number of combinations of arranging

(c)

Sikkim Manipal University

Arindam Parmar

Kshitij Panghaal

Kritartha Paul ChoudhuryG 1

Sandeep Gurung

(d)

‘By selection sequence’ is a method where any one of

the secret is kept fixed and the pixel information from the other three secrets is chosen at random alternately with the fixed secret. In Table 1 and Table 2 secret A has been kept fixed.

Table 1. Comparison of PSNR of the Decrypted Secrets By Its Sequence of Selection of Pixels from the Secrets

Sequence	PSNR value Secret A	PSNR value Secret B	PSNR value Secret C	PSNR value Secret D
Sequential	4.1985	3.4471	3.4369	3.4407
Random	3.0345	3.0529	3.0703	3.2535
By selection	4.9155	3.2962	3.3176	3.4644

Table 2. Comparison of Contrast of the Decrypted Secrets By Its Sequence of Selection of Pixels from the Secrets

Sequence	Theoretical Contrast	Experimental Contrast
		Secret A	Secret B	Secret C	Secre t D
Sequential	0.1052	0.101	0.099	0.106	0.096
Random	0.1052	0.098	0.102	0.099	0.101
By selection	0.1052	0.104	0.084	0.091	0.089

From Table 1, it is quite evident that sequential selection of secrets using multiple_info_hiding_algo gives a better result in terms of PSNR as the PSNR of each decrypted secrets is almost equal to the average of the PSNR of all the secrets, unlike when secrets are chosen at random. Table 2 helps to perceive that the contrast of the decrypted secrets is better when the secrets are chosen sequentially while encryption as compared to random selection.

• VI. Conclusion

This paper has successfully been able to suggest the following ideas for a given set of secrets (keeping in view the constraint on the dimension chosen for the images):

• 1.    Generation of cubical random pattern which correspond to the random grids generated.

• 2.    Each side of the cube is assumed to be a square random grid during encryption.

• 3.    Combining of random grid and recursively image hiding technique.

• 4.    The shares in isolation leak no information about the information contained in it.

• 5.    Both confidentiality and authentication can be achieved by this method of encryption.

• 6.    The cubical share reveals information at correct rotation and orientation of stacking.

• 7.    No extra pixel expansion introduced since simple random girds were used.

• 8.    The carrying capacity of each of the shares have been increased several folds.

• 9.    The decrypted information is free from distortion as random grids were used.

Upon comparing with other traditional VSS schemes by VC and RGs, the proposed benefits form the situation as it requires no codebook without introducing pixel expansion and increasing the carrying capacity tremendously. In total, the proposed scheme can carry more information than any other traditional VSS methods.

Fig.12. Implementation of Various Design Strategies in the Form of a Cube at Various Rotations along Its Dimensions. (a-c) Final output KAK Strategy (d-f) Final output Algorithm2

• VII.    Future Scope

The project can be extended further to incorporate the coloured images, the cipher can be obtained using the scheme discussed in [11] and then follow the same steps discussed above to generate the cubical shares. The cipher obtained by stacking the cubical shares can then be used to get the original image using the decryption scheme. There are different techniques that can be used for coloured images one of which is stated above.

• VIII.    Acknowledgement

The corresponding author deeply acknowledges the guidance and inspiration by his Ph.D. guide Prof. (Dr.) M K Ghose, Dean Academics, Sikkim Manipal Institute of Technology, Sikkim, India.