Мультипликация изображений с помощью внеосевого эффекта Тальбота

Целью мультипликации является одновременное формирование группы непересекающихся, идентичных изображений или пространственных частотных спектров некоторого объекта.

В настоящее время развитие методов мультипликации стимулируется как необходимостью совершенствования технологии производства интегральных схем, так и проблемой создания многоканальных систем обработки информации с параллельным анализом. Основной при использовании методов мультипликации в микроэлектронике является проблема получения изображений с высоким качеством. Такие мультипликаторы должны обеспечивать высокую разрешающую способность и малые искажения изображений. При создании многоканальных систем обработки во многих случаях требования к качеству мультиплицированных изображений и их пространственных спектров по сравнению с требованиями в микроэлектронике могут быть значительно снижены, однако в этом случае мультипликатор не должен вносить больших потерь света, т.е. должен обладать высокой эффективностью. Выбор конкретного метода мультипликации в системах обработки определяется решаемой задачей, а также видом используемых носителей информации (фотопленка, электронно-лучевая трубка и т.д.) и типом источника излучения (когерентный, некогерентный).

В настоящее время известен ряд методов мультипликации изображений и их пространственных спектров:

• 1)    Матрица точечных отверстий [1]. Этот метод характеризуется низкой разрешающей способностью и большими потерями света.

• 2)    Метод, использующий матрицу линз малого диаметра. Он дает лучшие результаты, чем [2,3], однако качество изображений также невысокое, поскольку линзы почти всегда обладают аберрациями и искажениями. Кроме того, такой мультипликатор работает с сильным уменьшением изображения (мал размер поля мультиплицированных изображений), что не всегда удобно для построения многоканальных систем обработки.

• 3)    Методы, основанные на явлении двойного лучепреломления и разного рода калейдоскопы [2,4,5]. Очевидно, что при необходимости получения большого числа изображений мультипликаторы, основанные на этих методах, будут громоздкими.

• 2.    Дифракция света на периодическом транспаранте

В настоящей работе предлагается способ мультипликации, основанный на свойстве саморепро-дукции изображений периодических объектов, основанный на эффекте Г.Ф.Тальбота.

Пусть пропускание единичного изображения будет t e (x,y), тогда пропускание прямоугольного транспаранта в виде матрицы из МхN единичных элементов можно представить в виде:

t(x,y)=te(x,y)⊗ m=M n=N

⊗ ∑∑ δ ( x - md_x , y - nd_y ), m =- M n =- N

где М и N - целые числа, d x - период матрицы вдоль оси x, d y - период матрицы вдоль оси y, ⊗ - операция свертки, δ - дельта-функция Дирака.

Известно, что амплитудное распределение соответствующее этому пропусканию будет наблюдаться, на так называемом, расстоянии Тальбота [6]:

z = _± d , _± = 2 k , k=i, 2,...,                (2)

mλ m где l и m - взаимно простые числа, λ - длина волны излучения, d-период транспаранта.

Распределение амплитуды в плоскости Тальбота будет:

E(x,y)=Ee(x,y)⊗ m=M n=N

⊗ ∑  ∑δ(x-mdx,y-ndy), m=-M n=-N

Таким образом, периодический объект можно представить как суперпозицию дифракционной решетки и мозаичного изображения составленного из единичных элементов.

Известно свойство дифракционных решеток мультиплицировать изображение периодического объекта в обе стороны от оптической оси. В этом случае в плоскости Тальбота, (изображения Фурье), в высших порядках дифракции, формируется сле- дующие распределение амплитуды: n=N

E(x,y)=Ee(x,y)⊗ ∑δ(y-ndy) n=-N n=N

= E_e ( y ) ⊗ ∑ δ ( y - nd_y )

n =- N

для порядков дифракции мультиплицированных вдоль оси X, и m=M

E(x,y)=Ee(x,y)⊗ ∑δ(x-mdx)= m=-M m=M

= E_e ( x ) ⊗ ∑ δ ( x - md_x )

m =- M

для порядков дифракции мультиплицированных вдоль оси Y.

Из-за фильтрующего свойства δ - функции в высших порядках дифракции произойдет вычитание тех элементов объекта, которые не перпендикуляр- ны оси, вдоль которой происходит мультипликация. Объект из двухмерного станет одномерным [7].

В приосевой области, где перекрываются все дифрагирующие световые пучки, наблюдается классический эффект Тальбота, т.е. плоскости Тальбота, располагаются вдоль оси на расстояниях удовлетворяющих условию (2). В то же время существует область пространства, где дифракционные порядки с разными знаками не перекрываются [7]. Этой области и соответствуют соотношения (4) и (5). В этих областях пространства самоизображение происходит вследствие синфазности волновых фронтов от одинаковых элементов разных единичных изображений [7]. Так как вне оси происходит перекрытие только ненулевых порядков одного знака, то и изображение будет формироваться только высшими порядками дифЕрсалкицифиа.за изображения в нулевом порядке будет удовлетворять условию:

ϕ =2n π , где n=1,3,5 ...N (6) то изображение в нулевом порядке будет позитивным, а в области геометрической тени в высших порядках дифракции - негативным.

В случае если выполняется условие:

ϕ =2n π , где n=2,4,6 ...2N (7) то и в нулевом и в высших порядках дифракции изображение будет позитивным. Расстояние между плоскостями самоизображения в высших порядках дифракции вдоль оси z, будут в два раза больше, чем расстояние между плоскостями самоизображе-ния, располагающимися вдоль оптической оси системы..

В связи с тем, что в плоскости наблюдения, не совпадающей с плоскостью периодического объекта, спектр поля объекта принципиально финитен, (как вследствие фильтрующих свойств свободного пространства, учитывающих расхождение в пространстве высших гармоник ограниченных пучков, так и вследствие волновой природы света, за счет влияния быстро затухающих волн), изображения, полученные в непараксиальной области, будут так же подвергаться искажениям. Известно [8], что в спектре ограниченного предмета, в параксиальной области, при движении от центра изображения в плоскости Тальбота, общее количество перекрывающихся гармоник не убывает. Убывает лишь число симметрично перекрывающихся гармоник, что и вызывает ухудшение качества изображений. При дифракции излучения в непараксиальной области, изображение формируется дифракционными порядками одного знака и граничная частота равная [9]

f = ^{1 N} (8)

Г 4p d где р - вещественное число, N - количество элементарных ячеек в транспаранте, d - период транспаранта, достигается на краю параксиальной зоны. Затем происходит только убывание общего числа пространственных гармоник в изображениях. Поэтому наилучшие изображения и по качеству и по интенсивности находятся на краю параксиальной зоны.

Ухудшение качества изображений за счет «разбегания» высших гармоник можно описывать, как и в параксиальном случае [9], коэффициентом качества Линфута:

∫∫|~t(f)|2s(λzf -xn)df kn=∞      ∫∫t(x)dx                            (9)

∞ где ∼ - знак преобразования Фурье над функцией, f -пространственная частота, s - когерентная передаточная функция периодического транспаранта как оптической системы, λ - длина волны, xn -координата единичного (элементарного) изображения, t(х) - функция пропускания единичного изображения. Отсчет координаты xn ведется не от центра изображения, как в параксиальном случае, а от края параксиальной зоны и в качестве t(x) выбирается одномерная компонента функции пропускания единичного изображения.

Таким образом, формирование самоизображений по механизму эффекта Тальбота соответствует модифицированному принципу Э. Аббе о двойной дифракции при формировании изображения [10]. Согласно последнему, при формировании самоизобра-жения можно выделить дифракцию на единичных элементах и дифракцию на совокупности периодически расположенных по полю предмета элементов, вследствие чего фазовая задержка различных составляющих углового спектра, необходимая для формирования изображения, происходит из-за того, что дифрагировавшее на одинаковых элементах разных единичных изображений излучение проходит разный путь в свободном пространстве. Поскольку оба типа дифракции происходят в одной плоскости, то можно формировать изображения в ненулевых порядках дифракции излучения на периодическом предмете, а не только вдоль оптической оси.

• 3.    Синтез изображений в ненулевых порядках дифракции

В [7] был рассмотрен механизм формирования изображений Тальбота в высших порядках дифракции. Согласно этому механизму, можно предложить множество интересных практических применений для эффектов, возникающих при дифракции света в область, где ненулевые порядки разного знака не пересекаются.

Так, например, можно синтезировать изображение периодического объекта в высших порядках дифракции. Если сложить в плоскости Тальбота изображение с распределением амплитуд, как в (4), и изображение с распределением амплитуд, как в (5), то получим:

E ( x , y ) = E_e ( x ) ⊗ ^m ∑^{= M} δ ( x - md_x ) ⊗ E_e ( y ) ⊗ ^{m =- M}                    (10)

n = N

⊗ ∑δ(y-mdy) n=-N что совпадает с выражением (3). Можно сказать поэтому, что происходит преобразование одномерного объекта в двумерный.

Эксперимент проводился по следующей схеме. Оптическая схема (рис.1) состояла из гелийнеонового лазера, объектива, полупрозрачного зеркала, периодического объекта и экрана. Объект, изображенный на рис.2а, изготовлялся методом дубящего отбеливания на фотографической пленке “Микрат - изопан” по методике, описанной в [11]. Периодический объект был чисто фазовым.

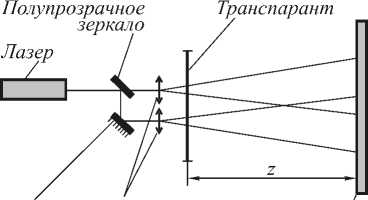
Глухое    Расширительные       / зеркало линзы             Экран

Рис.1. Оптическая схема для синтеза изображения периодического объекта в высших порядках дифракции.

Рис.2а. Периодический транспарант

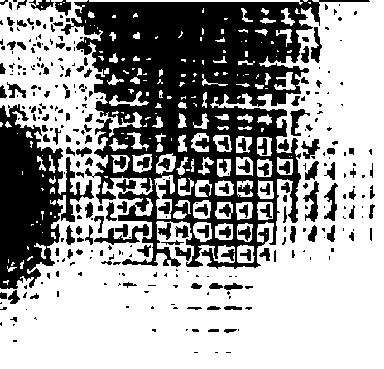
Рис.2б . Синтез периодического объекта в высших порядках дифракции.

На фотографии, представленной на рис. 2б., показан результат этого синтеза. Как видно из рис.2б. изображение в высших порядках дифракции подоб- но изображению в нулевом порядке. Но есть и отличия, так, например, в изображениях сформированных в ненулевых порядках отсутствует когерентный фон, поэтому они получаются более резкими и менее зашумленными.. Рассмотренная схема позволяет получить в одной плоскости четыре группы одинаковых изображений, что может быть использовано в системах обработки информации, когда небольшая кратность мультипликации.

• 3.    Литература

  • 1.    Kalestynsky A., Smolinska B. Spatial frequency sampling by phase modulation as method of generating multiple images. /Appl. Opt., 1977, v. 16 , ¹8, p.2261-2263.

  • 2.    Карпов Л.П., Блок. А.С. Мультипликация изображений и их пространственных частотных спектров. /В сб. Материалы IV школы по голографии. - Ленингр ад: АН СССР, 1973, с.136-155.

  • 3.    Kumar A., Senthil V., Vasu R.M. Multiple imaging with an aberration optimized hololens array. /Opt. Eng., 1989, 28 , № 8, p.903-908.

  • 4.    Frost B.S., Gourlay P.M. Coherent kaleidoscope I. Interference effects in a rectangular waveguide with point-sours input./ Appl. Opt., 1994, v.33, №3, p.373-383.

  • 5.    Gourlay P.M., Heckenberg N.R. and Frost B.S. Coherent kaleidoscope II. Experimental observation of sibling-spot formation in hollow and solid, square and rectangular waveguide./ Appl. Opt., 1994, v.33, №3, p. 384-396.

  • 6.    Patorski K. The self-imaging phenomenon and its application./ Progress in optics, 1989, v. XXVII , p.3-108.

  • 7.    Корфуненко О.А., Фещенко В.С., Фещенко Л.В. Оптическая обработка изображений периодических объектов. /В сб.: “Люминесценция и сопутствующие явления. Труды IV всероссийской школы-семинара (Иркутск,19-23 октября 1998 г.). Под ред. проф. Е.Ф. Мартыновича. - Иркутск: Изд-во Иркутского университета,1999.-стр.197-204.

  • 8.    Андреев Ю.С., Садовник Л.Ш., Тарновецкий В.В. Влияние конечных размеров периодических транспарантов на интенсивность изображений Френеля. /Опт. и спектр., 1987,т .63 , вып.3, с.620627.

  • 9.   Смирнов А.П. Изображения Френеля периодиче

    ских транспарантов конечных размеров. /Опт. и спектр., 1978, т. 44 , вып.2, с.359-365.

• 10.    Гудмен Д. Введение в Фурье-оптику. - М.: Мир, 1970.- 364 с.

• 11.    Выговский Ю.Н., Малов А.Н., Фещенко В.С. Управление формированием фазового рельефа в слоях дихромированного желатина. / Компьютерная оптика, 17 , ИСОИ РАН. Самара-Москва, 1997, с.75 – 85