Мультиверсионная модель программного обеспечения систем управления космическим аппаратом с ранжированием принятия решения

Введение. На этапе проектирования облика систем управления космических аппаратов происходит принятие решений по выбору состава мультиверсионного программного обеспечения системы с использованием метода нечеткого программирования. Это позволяет проектировщику задать степень «предпочтения атрибутов» и возможный «процент достижимости» целей при выборе того или иного варианта формирования состава мультиверсионного программного обеспечения [1–3]. Результатом, как правило, является множество недоминируемых решений задачи формирования мультиверсионного программного обеспечения системы управления.

Задача формирования комплекса мультиверсионного программного обеспечения систем управления космическими аппаратами представляет собой задачу условной оптимизации монотонной псевдобулевой функции.

Наиболее универсальным из всех методов дискретной оптимизации является метод полного перебора, когда для нахождения наилучшего значения целевой функции обследуются все допустимые решения [4].

В этом направлении разрабатывались алгоритмы двух основных типов: неявный полный перебор, где увеличение скорости нахождения оптимального решения реализовано через сужение области поиска и сокращение общего числа вычислений в алгоритме, и схема метода ветвей и границ с разбиением области поиска решения на меньшие подобласти.

Среди точных алгоритмов первого типа следует выделить процедуры, использующие для усиления вычислительных возможностей точных алгоритмов идеи сужения области поиска за счет особенностей функций-элементов решаемой оптимизационной задачи и наискорейшего обхода области поиска по соседним точкам, с использованием отношений на пространстве булевых переменных [5].

К алгоритмам схемы ветвей и границ [6] отнесены алгоритмы поиска решений на подкубах [7–8]. Процедуры этого вида различаются лишь способом организации разбиения области поиска решения на подкубы, т. е. способом представления исходной оптимизационной задачи в виде некоторого числа задач меньшей размерности [9].

Большое количество модулей мультиверсионного программного обеспечения систем управления космическими аппаратами, их избыточные версии, а также ограничения реальных потребностей такие, например, как стоимость разработки, внедрения и модификации системы, ставят пред проектировщиком задачу принятия решений по выбору оптимального состава мультиверсионного программного обеспечения системы с учетом ряда атрибутов [10–13].

При существовании достаточно большого числа альтернатив при их оценке в значительной мере сказываются качества самого лица, принимающего решение, его субъективные предпочтения. Поэтому, производя выбор лучшей альтернативы из ряда предложенных, нужно учитывать субъективность в оценках лиц, принимающих решений [14].

Модель общего ранжирования при выборе оптимального решения. В новых информационных технологиях принятием решений считают набор решений в условиях определенности, позволяющих выбрать однозначные, непротиворечивые, корректные решения на основе формализованных моделей объектов управления и окружающей их среды. Принятием решений следует считать и формирование неких вероятностных решений в условиях неопределенности [11].

К задачам поддержки принятия решений в новых информационных технологиях относятся все задачи, включая класс задач в условиях неопределенности, окончательное решение которых осуществляется вне используемой технологии. В этих случаях информацию преобразуют к виду, упрощающему и облегчающему принятие решений иными методами.

Можно констатировать, что в настоящее время для поддержки принятия решений используют различные методы и подходы, которые в совокупности дополняют друг друга. Принятие решений включает выбор последовательности действий и ее реализацию. Поддержка принятия решений основана на получении многовариантных решений с использованием разных методов.

Методология поддержки принятия решений включает разнообразные схемы и технологии, может реализоваться частично или полностью с использованием программно-информационных систем.

Простейшая модель принятия решения включает четыре основных, циклически повторяющихся этапа:

– сбор, анализ и преобразование данных;

– получение вариантов решений (альтернатив);

– разработка критериев оценки решений;

– выбор одного из вариантов на основе выбранных критериев.

Возможны разные условия и ситуации, в которых требуется принимать решения. Существуют разные уровни принятия решений. Верхним является концептуальный уровень. Он позволяет составить обобщенную схему. Технология принятия решений в общем случае включает следующие этапы:

• -    возникновение проблемы или задачи, требующей решения;

• -    формирование проблемы на вербальном уровне;

• -    поиск информации, необходимой для принятия решения;

• -    формализация постановки задач;

• -    анализ и обработка информации;

• -    формирование набора альтернатив;

• -    получение прогнозных оценок;

• -    оценка результатов принятия решения.

На первом этапе возникает проблема или задача, которая требует решения. Как правило, она формируется на вербальном (неформализованном) уровне общения.

После этого осуществляют поиск и сбор информации в аспекте данной проблемы или задачи. При этом собирают не только данные, необходимые для решения, но и информацию о методах решения подобных задач. После этого осуществляют формализацию или формирование проблемы на формальном уровне [15].

На этапе анализа и обработки информации осуществляют комплексную обработку, включающую компьютерные методы и экспертный анализ; прямой расчет и эвристические методы; оптимизационные методы.

Возможное изменение условий предусматривается получением наборов решений. Взаимоисключающие решения называют альтернативами. Поэтому для полноты и учета изменяющихся условий в результате анализа осуществляют формирование альтернатив, что представлено как важный этап в схеме принятия решений. Представление обобщенных данных осуществляют в виде, удобном для принятия решений.

Следующим этапом и одним из наиболее важных является этап получения прогнозных оценок. На этом этапе с использованием имеющихся вариантов решений, информации об условиях и методах получения прогноза получают прогнозные оценки, а также обосновывают выбор метода прогнозирования и метода верификации прогноза.

После получения комплекса данных: альтернатив, информации о динамике условий, прогнозных оценок, оценки надежности прогноза и др., производят комплексную обработку с использованием экспертного подхода. Эта схема может работать при разных технологиях и уровнях управления.

Следует подчеркнуть связь перечисленных этапов. Они образуют иерархическую последовательность. Если на одном из этапов отсутствует возможность его реализации, то переход к последующим не осуществляется. Поддержка при принятии решений означает, что группа этих методов направлена не только на получение решений, но и на подготовку рекомендаций для лица, принимающего решения. Таким образом, поддержка принятия решений включает три группы задач.

• 1.    Получение не одного, а совокупности решений.

• 2.    Подготовка критериев для оценки полученных решений.

• 3.    Выбор решения из имеющейся совокупности.

При формировании решений и их оценок существует проблема корректного извлечения необходимой информации.

Применение современных технологий и методов принятия решений требует применения формализованных данных. Поэтому эффективность методов получения решения и поддержки принятия решений зависит от формализации задачи. Так, при декомпозиции сложной задачи до операционного уровня и полной формализации условий решения задачи на этом уровне эффективно для получения решений использование методов исследования операций. При невозмож- ности декомпозиции и полной формализации используют методы статистической оценки, теорию нечетких множеств и др.

Выбор лучшего варианта формирования мультиверсионного программного обеспечения системы из всего множества возможных реализаций возможно произвести с помощью компенсационной модели многоатрибутивного принятия решений, которая позволяет выполнить общее ранжирования альтернатив на основе порядка их предпочтения по отдельным атрибутам и взаимосвязи между ними и определить наилучший вариант формирования мультиверсионного программного обеспечения.

Разрабатываемая модель принятия решений по составу мультиверсионного программного обеспечения системы предполагает ранжирование возможных вариантов их формирования в порядке предпочтения. Вариант, получивший первый ранг, является наилучшим. Использование в качестве входных данных только порядка предпочтения позволяет избежать масштабирования атрибутов качественного типа [16; 17].

Данная модель основывается на ранжировании альтернатив по отдельным атрибутам. На основе такого «частного» ранжирования определяется общий порядок предпочтительности альтернатив с учетом всех атрибутов и связи между ними.

Существует линейный метод назначения, который позволял выполнить общее ранжирование альтернатив [18]. Согласно данному методу, общий ранг рассчитывался как сумма рангов по отдельным атрибутам. При этом информация о взаимосвязи между атрибутами игнорировалась:

r -общ = Tj ij , i = 1, m,                                        (1)

j = 1

где m – количество альтернатив; n – количество атрибутов; r ij – ранг i -й альтернативы по j -му атрибуту; r – количество рангов ( r = m ).

Однако для большинства задач принятия решений и, в частности, для выбора варианта формирования мультиверсионного программного обеспечения системы, важно учитывать данную зависимость [19]. В связи с этим, на основе данного метода была разработана компенсационная многоатрибутивная модель общего ранжирования альтернатив в порядке предпочтения с учетом зависимости атрибутов.

Идея компенсации в данном случае заключается в учете зависимости между атрибутами: изменение значения одного из них приводит к изменению значений каких-либо других атрибутов.

Определим матрицу π как квадратную неотрицательную матрицу m × m , чьи элементы π ik представляют количество (или частоту) ранжирования альтернативы A i по r -му рангу. Матрица π формируется на основе матрицы ранжирования альтернатив по отдельным атрибутам D :

n

• ⁿ ik = Z I ⁽ D j ) • w ; i = 1, m ; ^j = 1, r ,                             (2)

i = 1

I (Dji) = ■ 1, если Di, = г, j                                                 (3) 0, если Djl * i, где I(x) – индикаторная функция; wl – весовой коэффициент l-го атрибута.

При различных весовых коэффициентах элементы матрицы п представляют сумму весов атрибутов соответствующего ранга. Предполагается, что весовые коэффициенты нормированы.

Очевидно, что π ik определяет вклад альтернативы A i в общее ранжирование. Чем больше значение π ik , тем более справедливо назначение альтернативе A i r -го ранга.

Определим матрицу перестановки Q , как квадратную матрицу m × m , чьи элементы Q ir = 1, если альтернативе A i назначается общий ранг r , и Q ir = 0, в противном случае. Целевая функция может быть записана в следующем виде:

mr maxZZ nikQir(4)

Q i = 1 j = 1

при условиях

r

Z Qr = 1; i = 1, m, j=1

m

ZQr=1; j=1,r.

i = 1

Условия означают, что альтернативе A i может быть назначен только один ранг и ранг r может быть назначен только одной альтернативе.

Обозначим оптимальную матрицу перестановки, представляющую решение указанной выше задачи линейного программирования, как Q *. Тогда, оптимальное упорядочение может быть достигнуто перемножением матрицы A, содержащей номера альтернатив, на Q *.

Рассмотрим пример модельный применения предлагаемой компенсационной многоатрибутивной модели общего ранжирования при выборе одной из трех альтернатив. Пусть все атрибуты имеют возрастающее предпочтение, т. е. чем больше значение атрибута, тем более предпочтительна альтернатива.

Положим, что ранги этих альтернатив по трем отдельным атрибутам соответствуют приведенным в табл. 1. Так, первая альтернатива имеет по первому атрибуту первый ранг, по второму – первый ранг и по третьему – второй.

Таблица 1 Ранжирование альтернатив по отдельным атрибутам

Атрибут		1	2	3
Ранг	1	A1	A1	A2
	2	A2	A3	A1
	3	A3	A2	A3

Ранжирование по отдельным атрибутам может быть представлено в виде матрицы D , элементами которой являются индексы ранжируемых альтернатив:

D = 2

На основе данной матрицы можно получить матрицу π, элементы которой представляют собой количество назначения альтернативе каждого из рангов. Так, первой альтернативе первый ранг был назначен дважды, второй ранг – один раз и третий – ни разу, что соответствует значения в первой строке матрицы:

n = 1

Для весовых коэффициентов w 1 = 0,2, w 2 = 0,4, w 3 = 0,4 элементы матрицы π изменятся следующим образом:

	" 0,2 + 0,4	0,4	0 "		" 0,6	0,4	0 "
п =	0,4	0,2	0,4	=	0,4	0,2	0,4	.                            (9)
	. 0	0,4	0,2 + 0,4		. 0	0,4	0,6 _

Оптимальная матрица перестановок Q*, определяющая общий ранг каждой из альтернатив, имеет вид

Q * = 010

Видно, что первая альтернатива (ей соответствует первый столбец) имеет общий ранг, равный единице (первая строка), вторая альтернатива получила второй ранг и третья – третий. На основе матрицы Q * получаем следующий порядок предпочтений:

A1 >  A2 >  A3. (11)

Компенсационная модель многоатрибутивного принятия решений позволяет выполнить общее ранжирование альтернатив в порядке предпочтения, основываясь на ранжировании по отдельным атрибутам и взаимосвязи между атрибутами. Достоинством данной модели являются уникальные преимущества при практическом применении. Все, что требуется от эксперта при сборе данных – задание порядка предпочтения альтернатив по атрибутам. Такой подход позволяет избежать трудностей, возникающих при создании шкалы оценки атрибутов.

Алгоритмы оптимизации. Алгоритмы неявного полного перебора. В модели с последовательной организацией программных модулей комплекс мультиверсионного программного обеспечения определяется состоящим из набора программных модулей последовательного исполнения, для чего вводится множество I, card (I) = I . Множество модулей делится на классы, т. е. вводится множество классов программных модулей ( J , card ( J ) = J ). Относя некий программный модуль к определенному классу, ему назначается решение соответствующей промежуточной «типовой» задачи управления или обработки информации. Объединение «типовых» программных модулей в комплексы способствует формированию процесса решения общей целевой задачи системы управления.

С целью реализации модулей одного класса назначается программный модуль, который, в свою очередь, для обеспечения гарантоспособности исполнения реализуется с применением методологии мультиверсионного программирования. Для каждого программного модуля в соответствии с исходными спецификациями разрабатывается S j , ( j = 1, J ) функционально эквивалентных версий. Таким образом, вводится вектор S = { S j }, ( j = 1, J ), элементами которого являются числа, равные количествам версий программных модулей ( S j – число версий модуля, решающего задачу класса j – реализующих модуль класса j ).

В результате определяется множество всех программных модулей K , тогда K = card ( K ) характеризует общее число программных модулей, включаемых в проектируемый программный комплекс.

Кроме того, определяется множество В , card ( B ) = I принадлежности задач классам, мощность которого равна числу задач в системе, а каждый элемент этого множества равен номеру класса, которому принадлежит задача. Таким образом, элемент В i множества В представляет номер типового модуля, с помощью которого решается i -я задача управления в общем управляющем комплексе.

Введем булевы переменные:

1, если для реализации i -й ( i = 1, I ) задачи

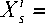
используется $ -я ( $ = 1, SB. ) версия модуля B i

0, в противном случае.

Введенные переменные разворачиваются в вектор участия, формально описывающий возможные варианты формирования состава мультиверсионного комплекса программ. Задача оптимального формирования мультиверсионного программного обеспечения состоит в нахождении набора мультиверсий, который определяет наибольшую надежность программного комплекса при соблюдении определенного уровня финансовых затрат на создание системы [7; 8; 20]. Сформулированная таким образом задача с использованием введенных ранее обозначение была формализована следующим образом:

l mахRNvs 1( X) = П R( X),                            (13)

i = 1

SBi             Xi где Ri (X) = 1 - П (1 - RBS) S - оценка надежности i-го программного модуля в составе муль-$=1

тиверсионного комплекса программ; R_BiS – оценка надежности s -й версии i -го программного модуля.

Ограничение на стоимость проектируемого комплекса программ имеет вид

C NVS 1⁽ X ) - B ,                                       ⁽¹⁴⁾

где

I ^S Bi

C nvs 1 ( X ) = Ц X S • C B . S ,                            (15)

i = 1 $ = 1

C_{B i S} – уровень финансовых затрат на реализацию s -й версии i -го программного модуля проектируемого комплекса программ.

Таким образом, в формальной постановке данного вида задача оптимального формирования мультиверсионного программного обеспечения формулируется как нахождение значений компонент вектора Х , таких, что функция надежности программного комплекса (13) принимает свое наибольшее значение при непревышении функцией стоимости (14) определенного значения В .

Для однозначного описания задач формирования комплексов мультиверсионного программного обеспечения, равно как и для конвертирования двух индексов булевых переменных X_S ⁱ , определенных в (12), в один номер компоненты вектора участия необходимо определить процедуру формирования вектора участия и, соответственно, алгоритм определения индексов компонент этого вектора [21–23].

Во второй оптимизационной модели, модели с последовательно-параллельной организацией программных модулей, мультиверсионный программный комплекс также рассматривается состоящим из набора задач управления последовательного исполнения (множество I , card (I) = I ). Подобно первой модели модули программного обеспечения по потребным функциям делятся на J типов, т. е. определяется множество типовых задач управления – множество классов задач – J , card ( J ) = J.

Но, в отличие от модели с последовательной организацией модулей, каждая задача I = 1, I программного комплекса реализуется не одним модулем, а некоторой совокупностью программных модулей, которая задается в векторе Ji, где Ji = {j1i,..., jJi}, следовательно, card(Ji) = Ji - число программных модулей, участвующих в решении i-й задачи и jk, к = 1, Ji -номер класса, к которому принадлежит k-й программный модуль.

Каждая типовая задача из множества J реализуется с помощью отказоустойчивого программного модуля, разработанного с использованием подхода мультиверсионного программирования, т. е. каждому элементу множества J поставлен в соответствие набор версий определяемого им модуля ( V k – множество версий модуля k , k= 1, J , S k = card ( V k ) число версий модуля k ). Таким образом, для каждого программного модуля в соответствии с исходными спецификациями разрабатывается S j , ( j= 1, J ) функционально эквивалентных версий, т. е. вводится вектор S = { S j }, ( j= 1, J ), элементами которого являются числа равные количествам версий программных модулей ( S j – число версий модуля, реализующих модуль класса j ).

Как и в первой модели, для формального описания структуры проектируемого комплекса мультиверсионного программного обеспечения вводится вектор участия X , компонентами которого являются булевы переменные X_kⁱ_S , такие что

1, если для реализации i -й ( i = 1, I ) задачи

X i = ‘

используется s -я ( s = 1, S _z) версия модуля к = ( к = 1, J ), J_k^{l                                             l}

0, в противном случае.

Аналогично модели с последовательной организацией программных модулей, задача оптимального формирования мультиверсионного программного обеспечения в данной модели заключается в определении набора мультиверсий, характеризующего наибольшую надежность программного комплекса при непревышении установленного бюджета на создание системы, т. е. формально задача оптимизации ставится следующим образом:

l mахRNvs 2( X) = П Ri( X),                             (17)

i = 1

где

а

J i

R i ( x ) = П R k ( x ), к = 1

Si jk

Rk (X) = 1 -П|1 - R s=1 V

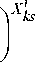
при том, что Ri (X ) – оценка надежности i-го набора программных модулей в составе мульти-версионного комплекса программ; Rki (X) – оценка надежности k-го программного модуля в составе i-го набора, R   – оценка надежности s-й версии k-го программного модуля в соста- jki,s ве i-го набора.

Ограничение на стоимость проектируемого комплекса программ определяется выражением

C nvs 2 ( X ) <  B ,                                      (20)

где

S i

I Jijk

^CNVS 2 ^{( X} ) = ^ ^ ^ ^XkS ' ^C j s , i = 1 к = 1 s = 1              ^k ’

C   – уровень затрат на реализацию s-й версии k-го программного модуля в составе i-го набо- jki ,s ра проектируемого комплекса мультиверсионного программного обеспечения.

Очевидно, что если среди множества всех граничных точек выделить две наиболее близкие к точке Х о , все координаты которой равны нулю, и наиболее удаленную от Х о граничную точку и определить уровни I min и I max точки Х о , соответствующие этим двум точкам, то станет возможным сужение области поиска решений, так как, бесспорно, решение полученной оптимизационной задачи будет принадлежать множеству, определяемому следующим выражением:

I max

S = U Oi(Xo), i=Imin где Xo - точка пространства булевых переменных, такая что X° = 0, i = 1, n.

Таким образом, чтобы найти решение задачи достаточно определить уровни I min и I max точки Х о и сравнить значения целевой функции в элементах множества S , определяемого выражением (22).

Данное свойство позволяет значительно уменьшить вычислительные затраты на поиск точного решения, ускоряя тем самым выполнение процедуры поиска. Мощность множества S определяется следующим выражением

I max card S = £ C nk , ^k = I min

где C_n^k – число сочетаний из n элементов по k .

Также неоспоримым является тот факт, что по причине аддитивного характера функций (15) и (19) наиближайшая к точке Х о граничная точка будет характеризоваться соответствием ее единичных координат наибольшим слагаемым указанных выражений. Т. е. для того, чтобы достичь из Х_о ближайшей к ней граничной точки, необходимо следовать пути наибольшего возрастания функций (15) и (21).

Алгоритм 1. Алгоритм определения уровня I min точки Х о .

• 1.    Принимаем I = 0, X e B 2 ? : X i = 0, i = 1, n .

• 2.    Формируем множество стоимостей версий программных модулей проектируемой системы

(M^   )

С, card(С) = n, где n определяется как n = ^ SB. или nNVS2 = ^ ^ S i i=1 *                       i=1 (k=1 jk v в зависимости от ре-

шаемой задачи.

• З.    Из условия C_k = тах C i , i = 1, n , X i = 0 определяем k .

• 4.    Назначаем X_k = 1.

• 5.    Если X _k принадлежит множеству допустимых решении, то устанавливаем I = I + 1 и переходим к 3, в противном случае, остановка алгоритма.

Алгоритм определения наиболее удаленной от Х_о граничной точки (алгоритм определения уровня I max точки Х о ) строится аналогично алгоритму 1, за исключением того, что в пункте 3 следует определять k из условия минимального прироста функции, т. е. определяется k , такое, что C_k = min C i , i = 1, n , X i = 0.

Схема поиска на множестве решений, определяемом выражением (22), реализована в алгоритме усеченного полного перебора.

Алгоритм 2. Алгоритм усеченного полного перебора.

• 1.    Определяем параметры I min и I max , соответствующие решаемой задаче.

• 2.    Принимаем I = I min .

• 3.    Определяем вектор X * , такой, что R ( X * ) = mах R ( X ), X е O I ( X 0 ).

• 4.    Повторяем пункты 2, 3 для всех I = I min , I max .

• 5.    За решение задачи принимается вектор X * , определяемый из условия R ( X * ) = maxR(X * ), I = * min , I max^.

Следует также выделить следующее свойство псевдобулевых функций (15) и (21): если две соседние друг к другу точки Х и Y отличаются значением некоторой i -й компоненты, причем X i = 0, то C ( Y ) = C ( X ) + C i , где C i – стоимость включения в структуру мультиверсии, соответствующей i -и компоненте вектора участия. Таким образом, вид ограничения в построенных оптимизационных задачах позволяет избавиться от полного вычисления выражений (15) и (21) в каждой точке, если обход области поиска решения организован как перемещение по соседним точкам. Полностью значение функции-ограничения для каждой из моделей вычисляется в некоторой начальной точке поиска. Все же последующие значения этой функции получаются прибавлением либо вычитанием соответствующей величины при переходе по соседним точкам

С целью утилизации вышеописанного свойства построенной оптимизационной задачи была реализована процедура обхода графа булевых переменных по соседним точкам, причем каждая точка области решений просматривается алгоритмом обхода только один раз, что позволяет избежать повышения вычислительной сложности поисковых процедур. В основе этого алгоритма обхода области поиска лежит возможность представления любого подкуба в виде объединения его нижней базовой точки и объединения непересекающихся подкубов меньших размерностей. Такой способ обхода области поиска реализован в алгоритме неявного перебора с обходом области поиска по соседним точкам.

Алгоритм 3. Алгоритм усеченного неявного перебора с обходом области поиска по соседним точкам.

• 1.    Определяем параметры I min и I max , соответствующие решаемой задаче.

• 2.    Принимаем X е B П : X, = 1 V i <  I _min, k = 0.

• 3.    С помощью алгоритма неявного перебора с обходом области поиска по соседним точкам определяем X_k ^* – точку, дающее наибольшее значение целевой функции на данном этапе.

• 4.    Генерируем следующую точку X е O X ₀ ( I min ), k = k + 1.

• 5.    Шаги 3, 4 повторяем C_n^{I min} раз, где C_n^k – число сочетаний из n по k .

• 6.    За решение принимаем точку X* = max X * , k = 1, C ^ mi ⁿ.

Алгоритмы схемы метода ветвей и границ. Во второй группе точных поисковых процедур начальная задача разбивается на несколько меньших по размерности подзадач через разбиение области поиска. Разбиение области поиска решения, в свою очередь, реализовано как разбиение пространства булевых переменных на множество непересекающихся подкубов, полностью покрывающих все пространство B ₂ ⁿ . Общая схема алгоритмов, построенных с использованием данного метода, выглядит следующим образом.

Алгоритм 4. Схема метода ветвей и границ (разбиение булевого гиперкуба на подкубы).

• 1.    Область поиска, представленная (в общем случае) подкубом в бинарном пространстве, разбивается на R непересекающихся подкубов.

• 2.    Определяется принадлежность граничных точек каждому из подкубов.

• 3.    Если r -му ( r = 1, R ) подкубу принадлежит хотя бы одна граничная точка, то с использованием методов неявного полного перебора находится и запоминается точка Х r подкуба, дающая лучшее значение целевой функции, удовлетворяющее ограничениям.

• 4.    Лучшее из «локальных» решений принимается за решение задачи f ( X *) = min, r = 1, R .

В общем случае предлагаются два метода разбиения нулевого гиперкуба на подкубы: разбиение B 2n на 2 ⁿ - ⁿ sub подкубов одинаковой размерности n_sub <  n и метод рекурсивного деления подкубов на два равных по мощности подкуба, размерность которых, очевидно, на единицу меньше размерности делимого подкуба. В основе разбиения пространства булевых переменных на подкубы лежит соответствующее свойство вектора-маски.

Заключение. Оптимизационные задачи, к которым сводится задача формирования комплекса мультиверсионного программного обеспечения, представляют собой задачи так называемого «рюкзачного» типа. Однако особенности целевых функций в оптимизационных моделях не позволяют для их эффективной реализации использовать алгоритмы решения задачи о рюкзаке, разработанные ранее.

Утилизация свойств пространства булевых переменных, в том числе и свойств и отношений подкубов, позволяет разработать эффективные регулярные процедуры реализации построенных оптимизационных моделей, определяющие точное решение задач оптимизации.

Выбор лучшего варианта формирования мультиверсионного программного обеспечения системы основывается на реализации многовариантных решений при применении различных методов многоатрибутивного принятия решений. Компенсационная модель многоатрибутивного принятия решений учитывает информацию о взаимосвязи между атрибутами. Идея компенсации в данном случае заключается в учете зависимости между атрибутами: изменение значения одного из них приводит к изменению значений каких-либо других атрибутов. Модифицированный многоатрибутивный метод упорядоченного предпочтения через сходство с идеальным решением позволяет найти наилучший вариант формирования мультиверсионного программного обеспечения системами в множестве альтернатив любой мощности.

Экспериментальные данные показывают преимущество по времени поиска решения алгоритма неявного перебора с обходом области поиска по соседним точкам перед алгоритмами схемы метода ветвей и границ.