MUSIC 2D-DOA Estimation using Split Vertical Linear and Circular Arrays

In wireless communications, two-dimensional direction-of-arrival estimation (2D-DOA) is of main interest and has many applications especially in radar systems [1]. It is also applicable to other variety of applications such as mobile communications, sonar, and seismology [2-8].

The estimation of the source angular components (i.e. azimuth and elevation) requires a planar array including the two-orthogonal uniform linear array (the L-shaped array) [2], the rectangular array [3], and the uniform circular array (UCA) [4-8]. Among these array structures, the UCA has gained attention due to its symmetry in detecting angles over 360 degrees in the azimuth plane [9]. The problem of estimating two-dimensional direction-of-arrival (2D-DOA), namely azimuth and elevation angles of multiple sources have received considerable attention in the field of array processing [1020]. Compared with the one-dimensional DOA, the 2D-DOA requires extensive calculations and the complexity depends on both the algorithm used and the array configuration. The maximum likelihood estimator [21] provides optimum parameter estimation; however, its computational complexity is extremely high. On the other hand, suboptimal solutions can be achieved by the subspace-based approach, which relies on the decomposition of the observation space into signal subspace and noise subspace. However, conventional subspace techniques for 2-D DOA estimation such as MUSIC [22] necessitate eigen decomposition of the sample covariance matrix or the singular value decomposition of the data matrix to estimate the signal and noise subspaces, and huge computation will be involved particularly when the dimensions of the underlying matrices are large. The use of circular arrays for MUSIC 2D-DOA has been addressed [23] but the search process for the impinging signals is performed in all available values of the elevation and azimuth angles which indicates a huge computational burden to accomplish the process and can be considered as blind 2D-DOA estimation technique. Therefore, in this paper we propose a novel array structure for fast and computationally efficient 2D-DOA estimation using MUSIC algorithm. This array is composed of two arrays namely vertical uniform linear array (VULA) which is centrally perpendicular to uniform circular array (UCA) and will be denoted by Split array. The VULA is used partially to estimate the elevation DOAs which define the search planes for determining the correlated azimuth DOAs by the UCA. Therefore, the 2D-DOA is performed sequentially and this will reduce greatly the required huge computations compared to the case when utilizing only the UCA especially for large array sizes and large number of sources. Also the determination of azimuth DOAs can be done in parallel for all sources in order to reduce the processing time. The paper is arranged as follows; Section 2 introduces and demonstrates the split array and structure. Section 3 depicts the 2D-DOA beamformer using Split array concept and its beamforming equations are drawn. In Section 4, the MUSIC algorithm for 2D-DOA using split array is examined and demonstrated for both the VULA and UCL and Section 5 shows some simulation results for detecting multiple sources in the presence of noise at different scenarios. Finally Section 6 concludes the paper.

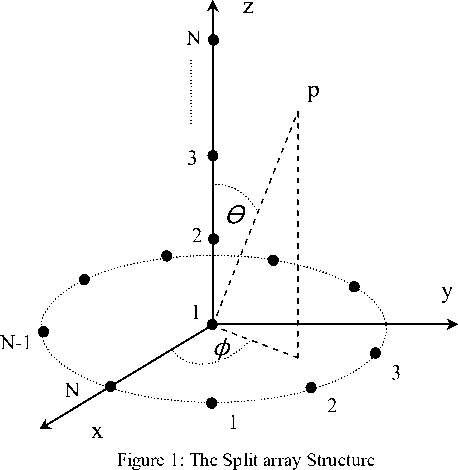
II. The proposed Split Array Structure

In this section we introduce the array geometry used for 2D-DOA. As shown in Fig. 1, the array is constructed by two perpendicular subarrays. The vertical subarray is a linear one-dimensional array of N elements and lies on the z-axis. The second subarray is a horizontal circular array of N elements and lies in the xy-plane. In array processing, the inter-element separation in both subarrays is usually assumed to be half of the wavelength which produces reasonable beam pattern without grating lobes or more-wider beams. The number of elements in the two subarrays may be different but in fact they must be the same because every detected elevation angle is associated with an azimuth angle and the increase in one array can detect a maximum number of angles and the maximum number of detected signals is limited by the smaller number of elements.

signals ( s₁(t),s₂(t),^ ,s_m( t)) impinging on the linear array, therefore we can write an expression for X_t( t) as:

X (t) = [а M)

а г (02)

а , ( 0m)]

or

X, (t) = Л ;S(t) + n(t)

Si(t)"

S2 (t)

Lsm(0J

+ n(t)

where: a_i(0₁) а_г(0₂) ... a_;(0_M) are the steering vectors of the linear array corresponding to the received signals, each of size N X 1, n(t) is the noise vector which is Gaussian with zero mean and variance о, , Л_г is the array steering matrix and equals [а_г(0₁) а_г(0₂) ... a_;(0_M)] with a size of X , ( ) is the received signal vector with a size of X 1.

The linear array steering vector at any direction is given by:

а г (e )= [1

g jTrsin(0) ^ 2 27rsin( 6 )

e

j(N -1 )тг sin

w f (4)

where the interelement separation is taken as half of the wavelength. For the circular array, the output signal is given by:

yc (t) = Wcr Xc( t)

where is the transpose of the circular array weights vector and ( ) is the array received signal vector given by:

Xc (t) =

[ac(01,01)

ac (02,02)

(   ,0 )]

S1 (0"

S2 (t)

+ n(0(6)

• III.    Split Array Beamformer for 2D-DOA Estimation

Fig. 2 depicts the proposed beamformer for the Split array where it consists of two stages; the first processes the signals impinging on the vertical linear array to determine the DOAs in the 6 -direction. The second stage is input with the detected 6 DOAs which represent the search planes in which the DOAs in the azimuth plane or in the 0 -direction are to be detected. Therefore the processing is done sequentially by first determining the output of the linear beamformer then applied to the circular beamformer. The output of the linear beamformer at any instant t can be written as:

У/ (0 = Wf X( t)                              (1)

Where W/' is the transpose of the array weights and X_t (t) is the array received signal vector. Assuming M

Lsm(0J or

Xc (t) = Л cS(t) + n( t)

where ac(01,01), ac(02, 02),^ ac(0M,0M) are the steering vectors of the circular array corresponding to the received signals, each of size X 1 , is the array steering matrix and equals:

[ac(01,01) ac(02,02) ^ ac(0m,0m)]

with a size of X . The circular array steering vector at any direction 0 is given by [24]:

a c (0,0) =

[ _e^^sin (^e) ^cos (0-^) _eJ^Nsin(e)c os(0-^)    _e^^sin ( ^e ) ^{c os} (0- ² ”)

(8) where the interelement separation is taken as half of the wavelength.

The arriving signals are time-varying and calculations are based upon time snapshots of the incoming signal. Then, for any of the two arrays, the correlation matrix R_xx is given by:

R_xx = E [X X ^H ]                                (9)

or

R_xx =ЛЙ₅₅Л » +Й _NN                      (10)

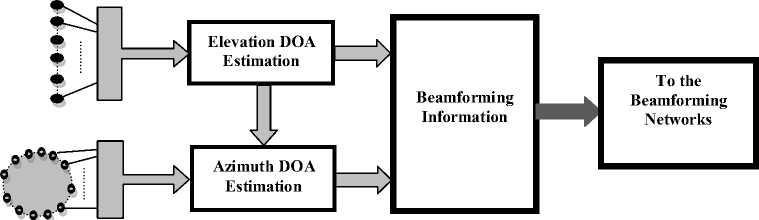
Figure 2: Split 2D-DOA Beamformer

where R_ss is M X M source correlation matrix, R_NN = o^I is M X M noise matrix, I is N X N identity matrix and A is N X M array steering matrix.

The array steering matrix is basic in the following calculations needed for MUSIC 2D-DOA as will be investigated in the following section.

• IV.    MUSIC 2D-DOA using Split Array

MUSIC is an acronym which stands for MUltiple Signal Classification which is an Eigen structure method. It depends on the properties of correlation matrix R_xx where the space spanned by its Eigen vectors may be partitioned into two subspaces, namely the signal subspace and the noise subspace and the steering vectors corresponding to the directional sources are orthogonal to the noise subspace. This MUSIC approach is a simple, popular high resolution and efficient Eigen structure method. From array correlation matrix R_xx we find M Eigen vectors associated with the signals and N-M Eigen vectors associated with the noise. Then choose the Eigen vectors associated with the smallest Eigen values. Noise Eigen vectors subspace of order N X (N — M) is constructed which is orthogonal to the array steering vectors at the angles of arrivals of the M sources.

For the vertical array, the elevation angles DOAs can be obtained from the peaks in the angular spectrum given by:

^PM USIC |Ие» ation^ ) = l_ai(₉)E_lNE H _Na_l(9 )| ⁽¹¹⁾

where E_lN = [e_t e₂ ... e_N_ _M] is N X (N — M) noise Eigen vectors subspace.

The angular spectrum obtained from the last equation is indeed symmetric about the vertical z-axis, therefore the azimuth angles cannot be obtained and this will be the function of the circular array which requires the estimated elevation DOAs as limiting planes of 0s to search for 0s. The limited planes of detected 0 s are actually the key benefit in using this array structure where searching blindly in all s is not computationally efficient method in 2D DOA estimation.

For the azimuth DOA estimation using the circular array we have a MUSIC azimuth angular spectrum given by:

^рмusic и zimuth ⁽⁰,⁰⁾ = | _{a c}(e,0)E_cNE»_Na_c(e,0)| ⁽¹²⁾ where E_cN = [e_t e₂ ^ e_N_ _M] is N X (N — M) noise Eigen vectors subspace from the circular array.

• V.    Simulation Results

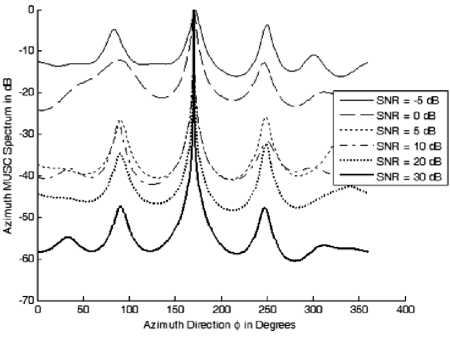
  In this section we will demonstrate the MUSIC 2D-DOA algorithm using Split array. Assuming 10 elements in both arrays and 5 signals impinging on the array having the following directions; (10^o, 30^o), (25^o, 80^o), (40^o, 170^o), (50^o, 250^o) and (70^o, 300^o). We will start with discussing the effect of the signal-to-noise ratio (SNR) on the DOA estimation at 1000 snapshots for averaging the signal correlation matrix . The results are depicted in Figs. 3 and 4(a-e) for both elevation and azimuth angles of arrival respectively.

In Fig. 3, the sources elevation angles are determined even if at lower values of SNR and especially for largely spaced sources. For close sources, the linear array can identify the angles of arrival at higher SNR values than the lower ones. On the other hand, the azimuth DOAs can be determined separately for each identified elevation angle as shown in Fig. 4 where we may apply the parallel processing techniques to reduce the required time for calculations.

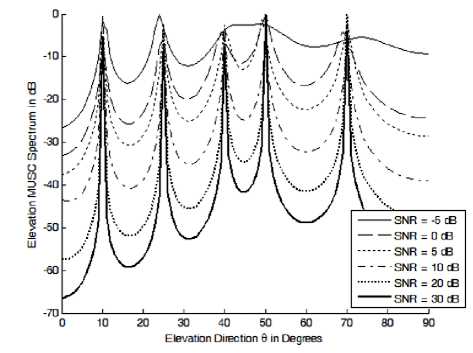
Figure 3: The elevation DOAs estimated at different SNR values

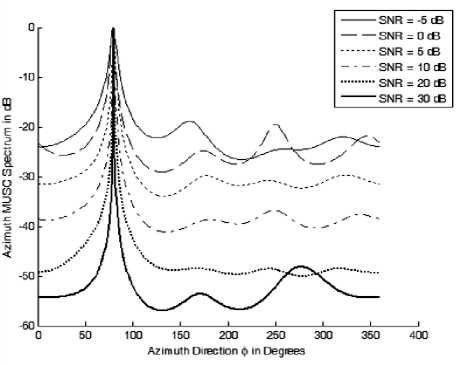
4 (c)

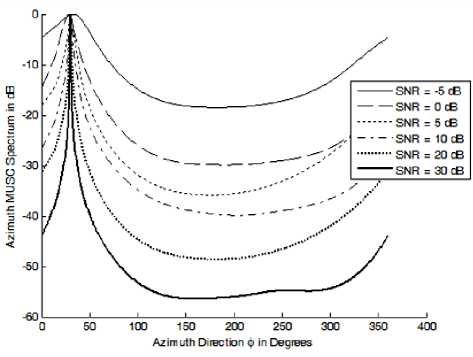
4 (a)

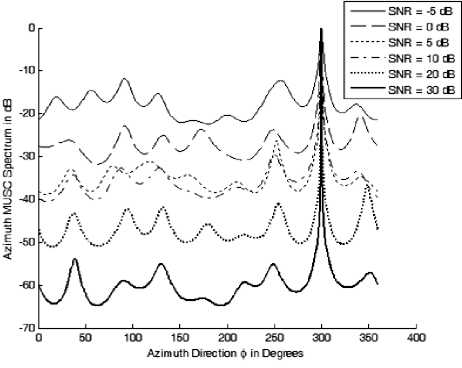
4 (d)

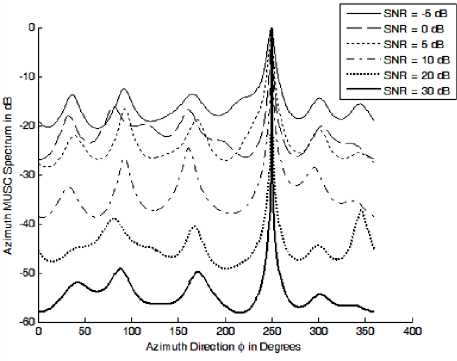
4 (b)

4 (e)

Figure 4: The different azimuth DOAs estimated after determining the elevation DOAs at different SNR values (a) azimuth spectrum at 6 = 10^o, (b) azimuth spectrum at 6 = 25^o, (c) azimuth spectrum at 6 = 40^o, (d) azimuth spectrum at о = 50^o, (e) azimuth spectrum at о = 70^o.

The DOAs can be identified easily because we search for a single source each time and the resulted MUSIC spectrum has very high resolution especially at higher SNR values. The separation of the azimuth DOAs calculations is necessary to remove the ambiguity so that we can relate the elevation DOAs to its corresponding azimuth DOAs.

The technique is also examined to determine the azimuth DOAs of the same elevation DOAs where we assume two sources coming from (30, 70o), (30o, 120o) and determine the resulted MUSIC spectra. Figure 5 shows the elevation MUSIC spectrum at different values of SNR where a single peak appeared, while in the azimuth spectrum as shown in Fig. 6; we have two peaks which correspond to the two co-elevation sources.

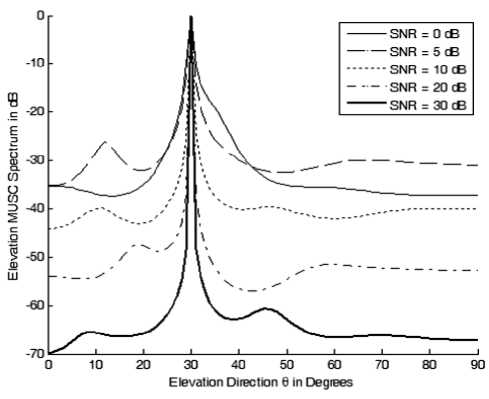
Figure 5: The elevation DOAs for the two sources (30, 70o), (30o, 120o) at different SNR

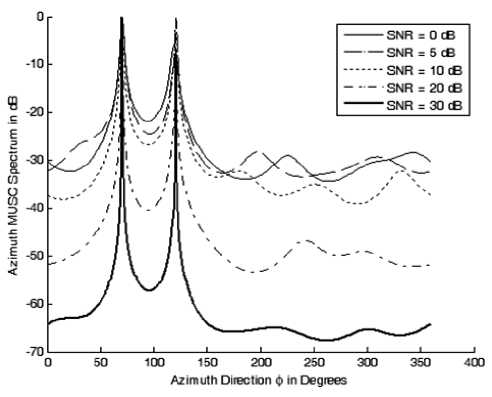
Figure 6: The azimuth DOAs for the two sources(30,70o), (30o, 120o) at different SNR

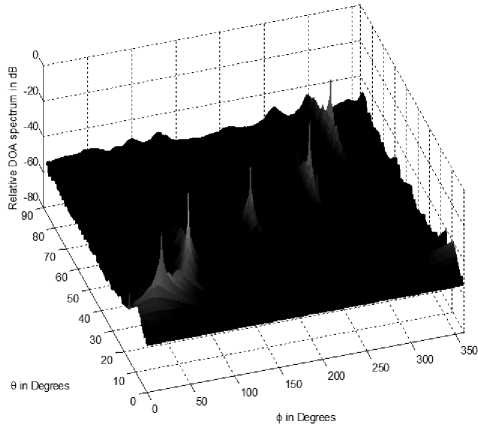
Figure 7: DOA spectrum for a conventional circular array of 10 elements showing DOAs at (10o, 30o), (25o, 80o), (40o, 170o), (50o, 250o) and (70o, 300o).

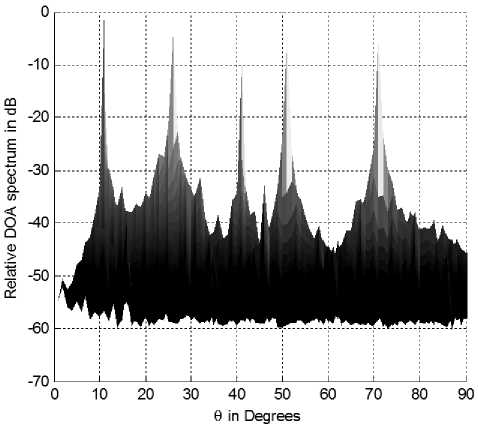
Figure 8: The elevation DOAs projection of Fig. 7

To provide information about the reduced processing cost we will examine the conventional circular array searching for 2D DOAs of the same angles in Fig. 3 and 4. The array structure is simply uniform circular array made of the same number of elements of that in the split array i.e. it has 10 elements only. The 2D DOA spectrum in this case is calculated over the whole elevation and azimuth angles (3D Pattern) and this is the main difference from the proposed technique as shown in Fig. 7. The projection of the DOAs to display the elevation and azimuth components are shown in Fig. 8 and 9 respectively where the peaks in each spectrum confirm the DOAs in Fig. 3 and 4 at SNR of 20 dB.

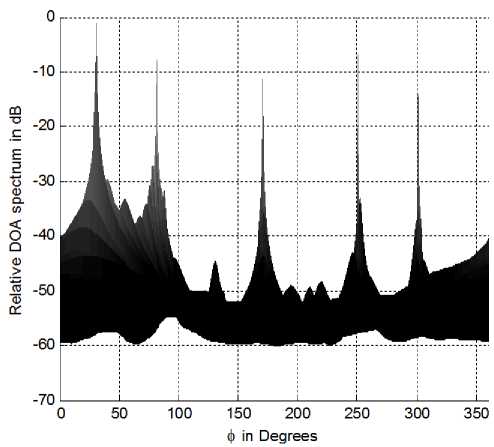
Figure 9: The azimuth DOAs projection of Fig. 7

The calculation times for the proposed algorithm compared Split array technique to the conventional circular array is demonstrated graphically in Fig. 10. For each technique, the calculations time increases with increasing the number of iterations needed for averaging but the proposed algorithm has lower slope than that of the conventional circular array and the time difference increases between the two methods especially when we increase the number of iterations.

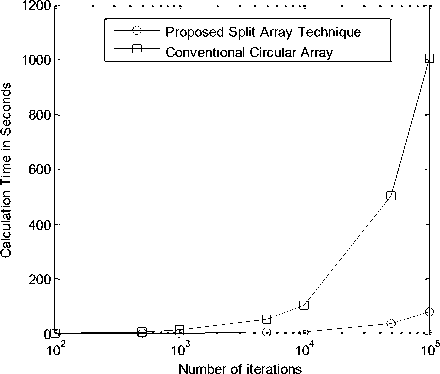
Figure 10: Time calculation comparison between the 2D-DOA using circular array with the proposed Split array technique.

• VI.    Conclusions

The techniques used in the 2D-DOA determination are to a large extent limited by the complexity of the calculations because it searches for the sources in all azimuth and elevation directions. In this paper, an efficient 2D-DOA technique using new array configuration is proposed and applied to the MUSIC algorithm. The array consists of a vertical linear array which is used firstly to determine the elevation DOA components and used subsequently as limiting search planes for determining the azimuth DOA components by a circular array in the horizontal plane. The azimuth DOAs are determined separately and may be in parallel to reduce the required search time. The technique is examined to determine the 2D-DOAs at different SNR values and show the capability to detect the sources even at lower SNR values near 0 dB especially for spaced sources. The technique is also able to detect co-elevation sources which have multiple peaks in the azimuth MUSIC spectrum while a single peak in the elevation MUSIC spectrum. It is also expected that the processing time is reduced greatly as the number of sources is limited by the number of elements in the arrays and is therefore very smaller than the number of search planes. The reduced processing time and simple design of this technique makes it applicable for accurate and practical 2D-DOA estimation.