(N, N) Secret Color Image Sharing Scheme with Dynamic Group

Published Online June 2015 in MECS

In a world teeming with hackers and identity thieves, data security is the holy grail of all online communications. From the low level password protection to the highest degree of encryption, online data users have been in search of a reliable method to store, transmit and retrieve data. One such trustworthy method is Visual Secret Sharing Scheme (VSSS). Secret sharing is a scheme aimed at achieving a task through dividing and reassembling data as and when required. These shares — pieces of information — act like multiple keys to a secret bank locker that could only be opened if all of them are in place. Similar to the requirement of a master, secondary and customer keys to open a locker, the secret shares will complete the targeted task only if all the pieces are assembled. This method eliminates the possibility of interception without compromising on the end-task, or in certain cases end-product.

The remainder of this paper is organized as follows. Section II reviewed the related literature and discusses the motivation of the work. Section III describes the design of proposed scheme. Section IV discusses the

Experimental Results. Finally section V concludes the paper.

• II.    A. Related Literature Review

  In a traditional (N, N) secret sharing scheme using visual cryptography proposed by Noar and Shamir [1], visual information is divided into n shares — one for each participant and the n shares are required to recover the original image. From its inception in 1994, many researchers have extended their ideas for secret color image sharing scheme using visual cryptography.

Blakley [2] and Shamir [3] independently proposed the concept of (r, n) threshold secret sharing scheme. This scheme divides the secret image into n shares and the shares were distributed to different users. Any r or more number of shares can reconstruct the secret while less than r shares could not recover the image. The succeeding studies were mainly related to the security of the keys.

Chih- Ching Thien and Ja-Chen Lin [4] developed a method in which secret image is shared by n shadow images, and any r shadow images(r<=n) can be used to restore the whole secret image. The size of each shadow image is smaller than the secret image.

In order to solve the problem of security during transmission of the large secret true color image, Guiqiang Chen et.al [5] developed the secret image sharing method based on the Lagrange’s interpolating polynomial. The n shadow images of the secret image were made by compression, substitution, encoding and disassembling back to the secret image. Then each shadow image is hidden in an ordinary image so as not to attract an attacker’s attention. The size of each stego image (in which a shadow image is hidden) is about 1/t times of the secret image. Any t images in the n stego images can be used to recover the original secret image.

Han-Yu Lin, and Yi-Shiung Yeh [6] proposed a dynamic multi-secret sharing scheme based on the oneway hash function. The major characteristics of its design are multi-use of the master secret shares and that different group secrets can be reconstructed according to the number of threshold values, which provides more flexibility. By applying successive one-way hash functions and the XOR operations, this scheme is secure against notorious attacks even though the pseudo secret shares are compromised.

Sian-Jheng Lin and Wei-Ho Chung [7] proposed a (t,n) VC scheme with unlimited n based on the probabilistic model. This scheme allows n to change dynamically in order to include new transparencies without regenerating and redistributing the original transparencies which reduces computation and communication resources required in managing the dynamically changing user group. But this scheme empirically suggested the value for t as 2 or 3.

The VSSM scheme developed by Tsung-lieh et.al [10] can share two binary secret images on two rectangular share images with no pixel expansion. Inkoo Kang et.al [11] introduced the concept of Visual Information Pixel (VIP) synchronization and error diffusion to attain a color visual cryptography encryption method that produces meaningful color shares with high visual quality. VIP synchronization retains the positions of pixels carrying visual information of original images throughout the color channels and error diffusion generates shares pleasant to human eyes.

Aarti et al [12] proposed a new (k,n)-threshold image sharing scheme using extended visual cryptography scheme for color images based on bit plane encoding that encrypts a color image.

• III.    B. Motivation Of The Work

In the scenario of dynamic user groups, where new participants are expected to join anytime, the scheme should provide the facility for generation of new shares to accommodate the new users. If the shares are to be generated with the traditional VC scheme, the shares of existing users need to be discarded, and the new shares need to be regenerated for all participants. Regeneration and redistribution of the whole shares require computing and communication resources.

Traditional Naor Scheme [1] suffers from the pixel expansion problem (m=4). Pixel expansion (m) is defined as the ratio of size of share images to the size of secret image.

This paper suggests ways to overcome such issues through a new (N, N) VC scheme for dynamic user groups where any number of new users can join without disturbing shares of existing users. This scheme has an additional feature of periodic renewal of shares. This scheme is free from the previously mentioned limitation -pixel expansion.

• IV.    Design of the Proposed Scheme

The proposed dynamic (N, N) VC Scheme has five modules.

• i.    Share Generation Phase

• ii.    Deleting existing shareholders

• iii.    Adding New shareholders iv. Periodic Renewal of Shares

• v. Reconstruction of Original Image

• A.    Share Generation Phase

In this phase, the original secret image I( г , с , d ) will be divided into N Shares using the Sharing Procedure. One share shall be randomly chosen to act as a master share with the administrator and remaining shares are distributed to N-1 users. The Sharing procedure for the proposed scheme shown in Fig.1 is clearly described in this section.

Sharing Procedure

Input: Secret image I of size г × с × d ,

Number of shares N,

Key Image of size less than secret image, Output: N meaningful shares of size г × с × d Step 1: Key Expansion Function

Expand key to the size equal to the size of secret image I.

Step.2: Source Matrix Formation

The source matrix s(i)=random Image of size г × с × d.

where i =1,2,3,.. n; п =       ( log₂N )

Step 3: Share Generation

S( =       ( X , Y )

where

{

s ( i -1)

Y ( i -1)

( s ( i )

^⎪ Si

Y =

^⎨ St-з ,

if i=1

if i ≤n+1

if i >n+1

if i ≤n if i =  +1

if i >n+1

if i =

Step 4: Share Permutation

St (1: r, j )= Key (1: r, j ) bitxor St (1: r, j )

where j mod N =i or j is the multiples of i ranging from 1 to column value c.

Recovery Procedure

In the receiver side, the secret image is reconstructed in one step using the formula,

Secret Image =  ⨁Si⨁…․⨁    ․

St ep 1 of Sharing Procedure generates a random key image and expanded into the size equal to that of the secret image. Random key image is used to increase the randomness of the shares and this key image need not be preserved as it is embedded within the shares. Step 2

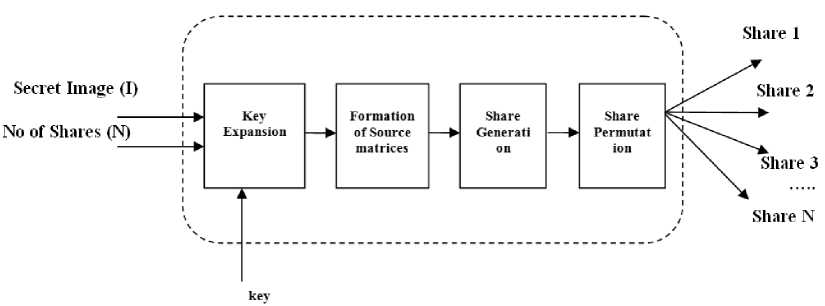
Fig. 1. SharingProcedure

computes the source matrix which acts as the base for share generation. The Source matrix s (i) for all values of i ranging from 1 to n where n =round (log₂ N) is generated by randomly generating images of size equal to the size of secret image.

The shares are then computed in Step 3 and 4. One share is randomly chosen as the master share. This share along with the number of share N is stored in the administrator database. The remaining shares are distributed to the shareholders.

• B.    Deleting an Existing Share Holder

This module describes the procedure to discard the share of a participant while leaving the group of trusted parties. Assume S^ be the share to be deleted and “^l be the master share. Then

5i = 1 ^⨁ 52 (1)

The discarded share will be superimposed with the master share using XOR as in (1). The number of shares N will be reduced by 1 and saved in the database along with the new master share.

• C.    Adding New Share Holders

For addition of new users, the same sharing procedure described in Share generation Phase (section III.A) is used. The input image is the master share and the N value is 2. This process generates two shares. One Share will be acting as master share and another will be issued to the new shareholder. Number of shares N will be incremented by 1 and is saved with the new master share in the database.

• D.    Periodic Renewal of Shares

The shares shall be renewed periodically by superimposing with the master share and subject to the sharing procedure using a new key to produce new shares and shall be distributed to the shareholders.

• E.    Reconstruction of Original Image

Number of shares (N) will be extracted from the database and N-1 shares obtained from N-1 share-holders are XORed with the master share to reconstruct the original image as shown in recovery Procedure.

• V. Experiments and Discussions

This section explains the proposed scheme with implementation for the (4, 4) Scheme and discusses the performance analysis. The impact of addition of new users and deletion of the existing users is also explained in this section.

The proposed scheme is implemented in matlab. Here the size of the input secret image is 200*150*3 and the key image size is 100*100*3 and number of shares (N) generated is 4. Fig.2 shows the share generation process for (4, 4) Scheme in which the input secret image is divided into 4 shares. The generated shares are meaningless and it does not reveal any relevant information about the secret image. Fig 2.b.shows the Master Share and the remaining three shares shown in Fig 2.c-2.e are distributed to the participants. To reconstruct the secret image, all the three shares are superimposed with the master share and the result is shown in Fig 2.f.

Fig 2.a

Fig 2.b

Fig 2.c

Fig 2.d

Fig 2.e

Fig 2.f

Fig 2. Share generation for the proposed (N,N) Scheme with N=4 a.Input Image b.Share1(Master Share) c.Share2 d..Share3 e.Share4 f.Recovered Image (4 shares)

Performance analyses of the recovered image quality in terms of PSNR and UQI for different images is shown in Table.1.The simplest and most widely used pixel wise error based measures are Mean Squared Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). The MSE is the squared intensity differences between the reference and the test image pixels and is defined by mn      2

MSE=1/mnEZ[ iij- j

PSNR=20*log 10 ( max f / sqrt(MSE))

Legend:

I -original image of size m*n.

I '-recovered image of size m*n.

max f - maximum intensity value that exists in the original image (255).The higher the PSNR, better is image reconstruction.

Universal Image Quality Index (UQI) is defined by modelling the image distortion relative to the reference image as a combination of three factors: loss of correlation, luminance distortion, and contrast distortion.

UQI=4c_X y (xy)' / (0 x2 ■ о/Пх'-у'²)

where

• A.    Security Analysis

For testing against attack, when 2 shareholders try to recover the image using their shares the recovered image is meaningless as seen in Fig.3a. The original image cannot be recovered even when 3 shares are superimposed. The resultant meaningless image is shown in Fig.3.b. So only when all N shares (N= 4) are combined, the original image can be recovered as shown in Fig 2.f.Thus when the hackers try to retrieve image by stealing any one of the shares they cannot retrieve the image .Thus this algorithm ensures security.

Fig 3.a

Fig 3.b

Fig 3..Security Analysis a..Recovered Image (2 shares) b.Recovered Image (3 shares)

х =   ∑ (х ) у =   ∑ (у )

σ =   ∑ (х -х′) σ =   ∑ (у -у′)

σ

N

∑ (х -х′)(у

-у′)

The range of UQI index is [-1, 1]. The best value 1 is achieved if and only if the images are identical. The recovered image shown in Fig 2.f has PSNR value of 45.833 and UQI value of 0.902.

The performance of the proposed VC scheme has been tested for 50 images and the PSNR and UQI values of the reconstructed image have been observed. These values are compared with the existing state of art VC scheme with half toning. Table 1 shows the comparative analysis between proposed scheme and the existing VC scheme.

From Table 1, it is observed that the proposed scheme performs well with no pixel expansion when compared to the existing VC scheme with the pixel expansion of 4.The average PSNR for 50 tested images is found to be 30.5 dB for the proposed scheme and 26.5 dB for the existing scheme,

• B.    Addition of New Shares

When a new participant is added to the group , the sharing procedure is applied to the master share with the N value as 2.

Table 1. Comparative Analysis of Proposed scheme with the existing Naor’s 1half toned VC scheme

S. No	Input Image	Metrics	Proposed VC Scheme	Existing state-of–art Naor’S VC Scheme for color Images (using Halftoning)
1		PSNR(dB)	31.60532	26.7101
		UQI	0.18626	0.10021
		PXEL EXPANSI ON	1	4
2		PSNR(dB)	29.40991	27.51443
		UQI	0.23708	0.18306
		PXEL EXPANSI ON	1	4
3		PSNR(dB)	30.45587	27.6497
		UQI	0.23718	0.23043
		PXEL EXPANSI ON	1	4

Fig 4.a

Fig 4.b

Fig 4.c

Fig.4. shows the impact of addition of a new share. When a new master share, share 5 and shares of the existing users shown in Fig.2.(c-e) are combined using XOR operation , the image recovered is shown in Fig.4.c with the PSNR value of 45.8533 dB and UQI value of 0.9127.

Table 2 shows the PSNR and UQI values for the recovered image obtained before and after additon of a new share.Results shows that addition of new shares do not degrade the visual quality of the recovered image.

Table 2. Performance Analysis of Proposed scheme before and after addition of a share

S. No	Input Image	Metrics	Before Addition (N=4)	After addition of a new Share(N=5)
1	Pim1.png	PSNR(dB)	42.001	42.001
		UQI	0.8917	0.8917
2	Im2.jpg	PSNR(dB)	25.064	24.972
		UQI(dB)	0.0863	0.0396
3	Im3.jpg	PSNR	45.853	45.853
		UQI	0.9127	0.9127
4	Im4.png	PSNR(dB)	42.624	42.624
		UQI	0. 9063	0.9063

• C.    Deletion of Shares

When any one of the participants is removed from the group, his share will be made invalid. Here for the process of deletion, share 2 shown in Fig 2.c is deleted. After deleting share 2, the new N value is 3.The new master share is shown in Fig.5.a. The remaining shares are same as shown in Fig 2.(d-.e).When the deleted share 2 is combined with all the other 3 shares, it will generate the image as shown in Fig 5.b.This shows that deleted share is made invalid in this scheme. When combining the existing three shares, the recovered image obtained is given in Fig 5.c.Thus this algorithm facilitates the process of deleting any user in group without regenerating shares of the other existing users.

Fig 5.a.

Fig 5.b

Fig 5.c

Table 3. Performance Analysis of Proposed scheme with addition and deletion of a share

S. No	Input Image	Metrics	Before Deletion (N=4)	After Deletion (N=3)
1	Pim1.png	PSNR(dB)	42.001	42.00
		UQI	0.8917	0.8917
2	Im2.jpg	PSNR(dB)	25.064	25.093
		UQI	0.0863	0.0364
3	Im3.jpg	PSNR(dB)	45.853	45.853
		UQI	0.9127	0.9127
4	Im4.png	PSNR(dB)	42.624	42.624
		UQI	0. 9063	0.9063

Table 3 shows the quality of recovered image in terms of PSNR and UQI of the recovered image before and after deletion of a share. Before deletion, number of shares N is 4.When a participant is excluded from the group, the new N value is 3. The quality of the recovered image when N=4 and after deletion of a share is examined.

From the table, it is observed that deletion of users also does not affect the quality of the reconstructed image.

• VI. Conclusion

This paper presents a (N, N) color secret sharing scheme for dynamic user groups. This scheme can be applied for any number of shares. The experimental results show that the size of the generated shares is same as that of the original image which leads to no pixel expansion. The recovered image has better visual quality when compared to other existing techniques. This scheme meets the requirements of addition and deletion of users without regeneration of shares for existing users. This scheme prevents the participants from cheating by using the deleted shares. Also, this proposed scheme has the benefit of periodic renewal of shares .The recovery phase of this proposed scheme involves simple Boolean operation and thus it reduces the computational complexity comparing to the existing techniques. Further research on this work will study about sharing more than one image.

• [1]    Naor.M and Shamir.A, “Visual cryptography,” in Proc. Advances inCryptography (EUROCRYPT’94), vol. 950, LNCS, pp. 1–12,1995.

• [2]    Blakely G.R. “Safeguarding cryptographic keys”, Proceedings AFIPS 1979 National Computer Conference, vol. 48, NewYork, USA, 4–7. p. 313–7,1979.

• [3]    Shamir A,” How to share a secret”, Communication of the ACM 22(11):612–3,1979.

• [4]    Chih-Ching Thien, Ja-Chen Lin, “Secret image sharing”, Computers & Graphics 26 765–770, 2002.

• [5]    Guiqiang Chen, Jianjun Liu, Liqin Wang, ” Color Image Sharing Method Based on Lagrange’s Interpolating Polynomial”, Health Information Science ,Lecture Notes in Computer Science Volume 7231pp 63-75, 2012 .

• [6]    Han-Yu Lin*, and Yi-Shiung Yeh , Dynamic Multi-Secret Sharing Scheme , Int. J. Contemp. Math. Sciences, Vol. 3, 37 - 42 , 2008.

• [7]    Sian-Jheng Lin And Wei-Ho Chung , ”A Probabilistic Model Of Visual Cryptography (t,n) Scheme with Dynamic Group”, IEEE Transactions On Information Forensics And Security, Vol. 7, No. 1, 197, February 2012.

• [8]    Z.Zhou, G.R.Arce, and G.Di Crescenzo, “Halftone visual cryptography”, IEEE Tans. On Image Processing, vol.15, No.8,pp. 2441-2453, August 2006.

• [9]    Robert Ulichney, “The void-and-cluster method for dither array generation”, IS&T/SPIE Symposium on Electronic Imaging and Science, San Jose, CA, 1993, vol.1913, pp.332-343.

• [10]    Tsung-Lieh Lin , Shi-Jinn Horng a, Kai-Hui Lee , Pei-LingChiu, Tzong-Wann Kao, Yuan-Hsin Chen, RayShine Run, Jui-Lin Lai,Rong- Jian Chen, “A novel visual secret sharing scheme for multiple Secrets without pixel expansion”, Pattern Recognition,2010 .

• [11]    InKoo Kang, Gonzalo R. Arce, Heung-Kyu Lee, “Color extended visual cryptography using error diffusion”, IEEE Transactions On Image Processing, Vol. 20, No. 1, January 2011.

• [12]    Aarti, Pushpendra K Rajput,”An EVCS for Color Images with Real Size Image Recovery and Ideal Contrast Using Bit Plane Encoding” I.J.Computer Network and Information Security, 2014, 2, 54-60

• [13]    Mohamed Fathimal.P,Dr.P.Arockia Jansi Rani, “Bidirectional Serpentine Scan Based Error Diffusion Technique for Color Image Visual Cryptography” , International Journal of Science, Engineering and Technology Research,2014

• [14]    Mohamed Fathimal.P,Dr.P.Arockia Jansi Rani, “K out of N Secret Sharing Scheme for Gray and Color Images”, IEEE International Conference on Electrical, Computer and Communication Tchnologies, March 2015.