N-version programming for nanosatellite telemetry processing

The key technical challenge in the field of software creation is increasing its reliability in terms of fault tolerance. Among the existing methods built on the principle of software components redundancy, the multi version approach (MVA) occupies a special place, mainly due to the periodic emergence and fading of interest in it in the scientific literature. The multi-version approach, also known as N-version, was first proposed to solve the problem of increasing software reliability in the early 70s. XX century. It should be noted that a number of foreign researchers consider N-version programming only as one of the variants of MVA [1], while in most papers these definitions are synonymous. Over the next two decades, this method received theoretical development, mainly in the work of a group of American researchers led by A. Avizhenis and his graduate students at California State University [2]. The main fundamental principles of this approach were formed, reflected in the expression N ≥ 2, meaning that if the number of program versions is more than or equal to two, the system is multiversioned. Despite the abundance of publications by A. Avizhenis and his colleagues during the 1970s – early 2000s, as well as the language of these works is, in our opinion, rather complex, the basic principles of MVA are simple. Independent development teams are expected to create two or more versions of the same program within given specifications. Running these programs (multi-versions) helps to identify patterns of software errors and failures, thereby allowing you to select the optimal version of the program. Within the framework of the classical MVA, three main elements are distinguished:

1.    The initial specification process and N-version programming are designed to ensure the independence and functional equivalence of N number of independent software development attempts . 2.    The final product (program) created within the framework of the profit center approach and having attributes of parallel execution with certain cross-points and comparison vectors for decision making . 3.    The environment that ensures the implementation of the MVA program provides decision-making algorithms at given cross points [2].

The concept of diversification or variety of software design is introduced, but the difference between multi-channel, redundant software and multi-version methods is emphasized. The idea of using a system with n parallel channels and a voting algorithm assumes that independent failures occur within individual versions or software modules and do not affect the system as a whole.

The principle of using n parallel channels with a voting algorithm is a traditional method for increasing the reliability of both hardware and software of a technical system. In this case, the ra- tionale for the MVA with n versions of programs (software modules) embedded in it lies in the following postulates [3]:

–    channels remain independent of each other in all cases ; –    software glitches always lead to disagreement between duplicate channels ; -    if the voting algorithm is functioning correctly, the probability that at least two channels (N > 2) out of the total number n corresponds

p ( m >  2) = 1 - p ( m = 1) - p ( m = 0)

where m is the number of matching channels; p is the probability of failure of any of them upon input signal. The probability of a system error in this case will be

1 - p ( m >  2) = p ( m = 0) + p ( m = 1) = pⁿ + n (1 - p ) p^{n - 1}.

Thus the use of multi-version diversification leads to a certain improvement within one program channel:

p = 1 pⁿ + n (1 - n ) p^{n - 1}    p^{n - 1} + n (1 - p ) p^{n - 2} •

In the last decade the MVA has been developed in the works of a number of domestic and foreign researchers [4–18]. Thus in work [18] the use of this approach for creating fault-tolerant software for dynamic systems (unmanned aerial vehicles) is considered. It should be noted that the use of MVP in the design of aviation software was declared in the early stages as the main area of successful application of this method [1; 18]. However, this use of profit center, in a sense, contradicts the classical concept of profit center (described by A. Avizhenis in his “Methodology” [2]), which is built around the software design process, and not its subsequent operation .

The problem of MVA usage

After MVA first arose, it was not criticized by the scientific community for a long time, mainly due to its theoretical significance. Despite the abundance of scientific literature on the topic of using MVA for processing various categories and types of data, the methodology for implementing this method is extremely poorly covered. In this regard, the above-mentioned study [19–21] compares favorably. The authors of the work describe in detail the entire algorithm for organizing an experiment to test the MVA method for analyzing data obtained from the conditions specified within the experiment. This study is especially important for us because the authors concluded that MVA is ineffective (although they point out that this conclusion is only valid within the framework of the experiment they conducted). We decided to repeat this experiment with changing parameters in terms of data type and volume.

Now we turn to the description of the experiment. The programs used in the experiment, according to the conditions, were written in the Pascal programming language. Due to the fact that this language can be considered outdated, we decided to write programs in the more modern Python language (or C++). The authors of the experiment proposed 27 versions of the same program, written by teams of programmers independent of each other. One version – the 28th – was defined as the “reference” and was used to calibrate the remaining versions. In this work, the number of program versions was increased to 50 (see table).

Data on multiversion failures from the results of the Knight and Levison experiment

Version	Failure	Reliability	Version	Failure	Reliability
1	2	0,999998	15	0	1,000000
2	0	1,000000	16	62	0,999938
3	2297	0,997703	17	269	0,999731
4	0	1,000000	18	115	0,999885
5	0	1,000000	19	264	0,999736
6	1149	0,998851	20	936	0,999064

Version	Failure	Reliability	Version	Failure	Reliability
7	71	0,999929	21	92	0,999908
8	323	0,999677	22	9656	0,990344
9	53	0,999947	23	80	0,999920
10	0	1,000000	24	260	0,999740
11	554	0,999446	25	97	0,999903
12	427	0,999573	26	883	0,999117
13	4	0,999996	27	0	1,000000

There are two options for approaching the generation of the proposed program versions :

• –    directly writing programs manually, as was done in [19];

• –    modeling of software versions based on mathematical models .

Since given specific parameters software versions are expected to be largely similar if not identical, the involvement of human resources for their creation cannot be considered advisable. In this regard the optimal solution should be the use of a mathematical model for the formation of subsequent versions of a given software. Thus, we created a reference version of the program, which was then reproduced 49 times using the mathematical methods presented below.

To implement the objectives of this article we consider the MVA model using the example MVA structural sub model. T his approach was shown for the first time in [22] and is of particular interest because it includes the basic principles of MVA within the framework of software reliability theory. Within this method, it is possible to combine functional and temporary failures into a single value. This allows you to build an analytical model based on both functional and performance failures. In the MVA sub model, time is considered as a constant value and is measured from the moment of running multi versions of the program. For this model the following assumptions have been made:

• –    software versions are conditionally independent of each other in a given input ;

• –    failure times of software versions for a given input are represented by equally common random variables with probability density f_F ( t ; ν ) depending on d dimension vector of the parameter ν = (ν₁, ..., ν _d );

• –    execution times of software versions for a given input represent uniformly distributed variables with probability density f Е ( t ; ^ψ ) depending on b dimension vector of the parameter : ψ = (ψ₁, ..., ψ _b );

• –    the execution time of the voting algorithm is negligible compared to the time required to implement each version ;

• –    due to the real time constraint, the system must perform correct decisions in the time interval τ > 0.

Next, we present a modified version of the MVA implementation in a given subsystem based on [22]. The distribution function F_F ( t ; ν ) gives the probability of failure of the first version of the program up to t , taking into account the failure of functionality. In this case the probability that the first version has a functional failure is

P f (τ;ν,ψ)= ∫ ^τ F F ( t ; ν)f E ( t ; ψ) dt _.

Next we assume that each version produces the correct result before τ :

τ

P_e (τ; ν, ψ) = ∫ [1 - F_F ( t ; ν)]f _E ( t ; ψ) dt .                                ₍₂₎

In this case, a system performance failure, as well as a temporary failure, occurs if none of the versions are completed before a given time τ :

τ

Pne (T;^) = 1 - J fE (;^)dt = 1 - FE (t;v)•

Next, we will consider a model with multi versions of the program. The temporary failure MVA of the system is ( n = 2 m – 1) for a given input in the event that most versions do not output processed data (finish their operation) during - ^T:

n

Pf (т; V) = X n 3 = m

n

I C(t; v)[1 - P ne (т; V)] ⁿ - ^{n 3}

I ⁿ 3 J

In case the majority of versions completed on time (before τ ), there is a high probability of functional failure of the entire system (most of the results are erroneous):

n n

P f ^(т; ^v, v) =

X      P n ² (т; v, v)[1 — P f (т; v, v)] n - n ² .

n 2 = m \ n 2 J

On the contrary, most of the results are correct (multi versions ran successfully):

n n

P ok (т; v, V) = X      I ^Pe 1 (T; v, V)[1 - P e (т; v, V)] ⁿ - n ¹

n 1 = m I ⁿ1 J

Finally, equation (7) shows the absence of both the majority of positive and the majority of negative results :

^Pnm ^(т; ^v, v) = ^{1 -} P f ^(т; v) ^- P ok ^(т; ^v, v) ^- P f ^(т; ^v, v)-

Processing telemetry information from small nanosatellites

Telemetry data transmitted to the ground control complex (GCU) can be in various formats, including texts, images, audio and video files.

Telemetry systems consist of the following elements:

• 1.    Data collection system.

• 2.    One of the following multiplex systems:

  – separated by frequency (frequency multiplexing);

  – time-separated (discrete, time multiplexing);

  – hybrid systems, which are a combination of systems separated by frequency and time.

• 3.    Modulator, transmitter, antenna.

• 4.    Wave-forming and transmitting communication channel .

• 5.    Antenna, RF receiver, intermediate frequency section, signal demodulator .

• 6.    Demultiplexing system for frequency and time systems, as well as their hybrids .

• 7.    Data processing system [23].

The first six elements presented are responsible for collecting various physical data, converting it into an electronic signal, and then converting it into various frequencies, taking into account sampling for the purpose of transmitting it. Transmission signal frequencies typically fall within two ranges: 1435–1535 MHz and 2200–2290 MHz. Without dwelling in detail on the wave formation system, let us consider the fifth, sixth and seventh elements of the presented system. They consist of hardware responsible for receiving signals from the spacecraft, as well as hardware and software that carry out subsequent processing of data and their conversion into design formats. The demultiplex subsystem ensures the separation of frequency and discrete signals and their direction from individual sensors into the correct channels, after which the data can be displayed, recorded and further processed.

Let us turn to the problems that arise at the stage of processing telemetry information. Due to the nature of their activities, spacecrafts must provide compact, undistorted and accessible data libraries in the shortest possible time period. In this regard, one of the main problems is the limited bandwidth available for transmitting telemetry data. The available bandwidth is limited by the capacity of the communication system and the distance between the spacecraft and the ground station. This limited bandwidth poses a challenge for processing and analyzing telemetry data in real time.

Another challenge is the complexity of the telemetry data architecture. Telemetry data from a spacecraft usually consists of a large number of parameters, each having its own range of values and units of measurement. Analyzing these data requires specialized knowledge and experience that may not always be available.

Finally there is the risk of data loss or corruption during transmission. In some cases telemetry data may be lost or damaged during transmission due to interference or other factors. This may result in incomplete or inaccurate data, which can affect the analysis and decision-making process.

Processing spacecraft telemetry data is one of the most challenging tasks in the field of space data processing. Spacecraft telemetry data formats are complex and varied, and data format definitions vary among spacecraft platforms. Common data formats include PCM frame format, packet format, mixed frame format, cycle count frame format, and so on. With the advent of the new platform, the number of formats is constantly increasing. Spacecraft telemetry data formats have a number of complex characteristics: the formats have hierarchical and nested structures that must be processed in cross-frames; formats have complex parameter dependencies. The spacecraft telemetry data processing model of the existing mission data processing software is based on the “Frame – Field” structure. Different frame formats are described by different methods for processing telemetry frames, and each field in the frame format describes the format of a specific parameter. This model has the following problems:

• 1.    The descriptive ability of the method for processing one telemetry frame is limited, which does not allow adaptation to the characteristic: the formats have a hierarchical and nested structure that must be processed cross-frames .

• 2.    Complex dependencies between parameters cannot be described effectively.

• 3.    The versatility and scalability of the model are poor. A new change (even a small change) in the data format leads to a restructuring of the frame processing method, which means frequent changes to the program code .

Thus, the existing model for processing spacecraft telemetry data, based on the “Frame-Field” structure, is difficult to adapt to the real situation of frequent changes in spacecraft telemetry data formats, especially during high-frequency flights. It is necessary to develop a new model for processing spacecraft telemetry data, which has greater expressiveness, greater versatility and scalability and solves the above problems [24].

The key differences between telemetry data obtained from nanosatellites, in contrast to standard spacecraft, include the conditions for their generation: for example, large devices are able to accommodate a larger number of components that provide system redundancy, thereby increasing its fault tolerance in an aggressive space environment (to in particular, ionizing radiation) [25].

Early samples (first generation) of specialized software for nanosatellites include the PolySat software architecture for CP series devices. The highly resilient hardware platform was built primarily using redundant components; their relative low cost and low power consumption made it possible to build a system with a high degree of redundancy. Fig. 1 shows the spacecraft hardware design.

The designed spacecraft operated in three modes: preparatory (pre-ops), normal (normal-ops) and emergency (contingency). In this case, the choice of mode for communication and the command and data controller (C&DH) is carried out independently. The latter is responsible both for various aspects of the system’s operation and for the collection, processing and transmission of telemetry [25–27]. Data collected from three satellites in the constellation was collected and stored in an I2C serial asymmetric bus in an electrically erasable flash memory. The memory capacity was no more than 256 kB, which significantly limited the operational characteristics of the nanosatellites. The second generation of software is built on Linux; thus, the author of [25] offers his own version of a software package for receiving and processing telemetry.

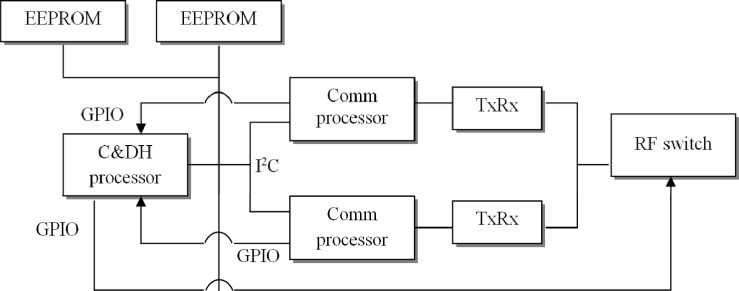
Payload

Рис. 1. Пример аппаратной блок-схемы резервирования коммуникационной системы

• Fig. 1.    Example of hardware block diagram of redundant communication system

In our case, telemetry information received from ReshU-1 is stored in log files (log files; CSV extension) with all data frames (Fig. 2–3). Moreover, the frames for each team are different. The data is parsed by a parser and then stored in the laboratory database. Log files are a common format for this type of information, such as TMI. Modern measurement information systems are capable of generating constant streams of this file format, providing information about the operation and state of the system.

Integration of a multi-version approach into the telemetry processing

One of the important steps is the integration of a multi-version approach into the telemetry processing system. This involves creating a framework that can handle multiple versions of an algorithm and determine the final result based on a consensus of versions. The system must also be designed to handle any errors or inconsistencies that may arise during the processing of telemetry data .

radio: { name: "gr-satnogs”, version: "v2.3-compat-xxx-v2.3.4.0", ▼ parameters: { soapy-rx-device: "driver=rtlsdr", samp-rate-rx: "2.048e6", rx-freq: ”435380000", file-path: "/tmp/.satnogs/data/receiving_satnogs_8101204_2023-08-31T22-36-08.out", waterfall-file-path: "/tmp/.satnogs/data/receiving_waterfall_8101204_2023-08-31T22-36-08, decoded-data-file-path: ”/tmp/.satnogs/data/data_8101204", doppler-correction-per-sec: null, lo-offset: null, ppm: null, rigctl-port: "4532", gain-mode: "Overall", gain: "22.9", antenna: "RX", dev-args: null, stream-args: null, tune-args: null, other-settings: null, dc-removal: null, bb-freq: null, bw: null, enable-iq-dump: "0", iq-file-path: null, udp-dump-host: null, udp-dump-port: 57356, wpm: null, baudrate: "19200", framing: ”ax25"

} latitude: 38.048, longitude: 23.739, elevation: 104, frequency: 435380000

Рис. 2. Пример записи метаданных с МКА ReshU-1

• Fig. 2.    ReshU-1 CubeSat metadata sample

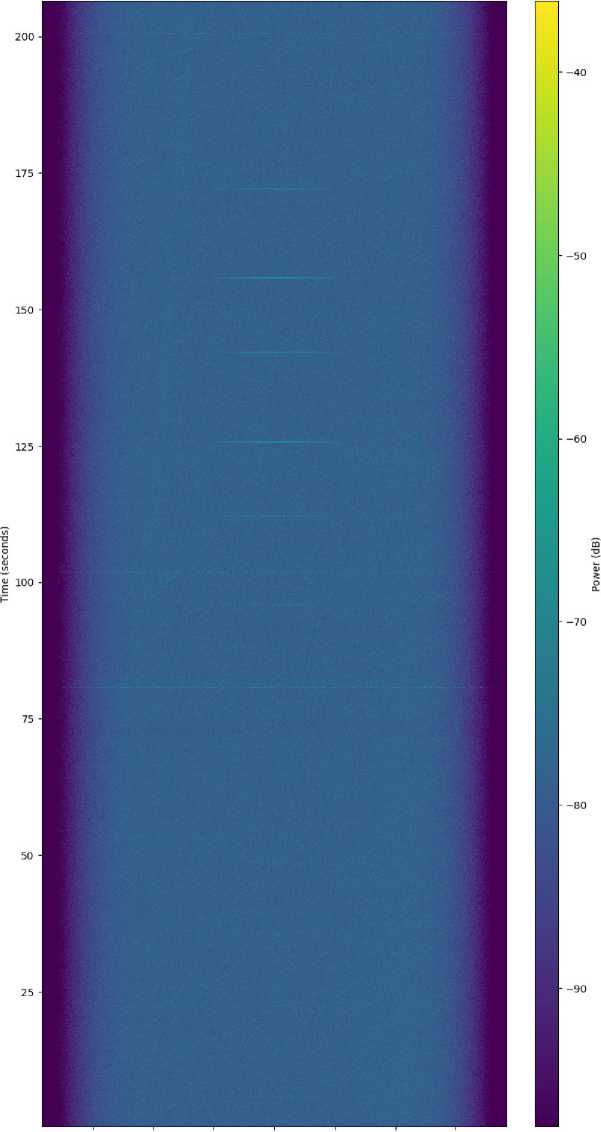
30      -20      -10       0        10       20       30

Frequency (kHz)

Рис. 3. Участок спектрограммы сигнала телеметрии МКА ReshU-1

• Fig. 3.    ReshU-1 CubeSat telemetry signal spectrogram

Integrating a multi-version approach into telemetry processing has several advantages. Firstly, it improves the reliability and accuracy of telemetry data by reducing the likelihood of errors or inconsistencies. Secondly, the amount of data that needs to be transmitted to the ground is reduced, since only the final result, which is determined by version consensus, is transmitted. This can lead to significant cost savings and increased efficiency

Fig. 4 presents an algorithm for ranking telemetric information

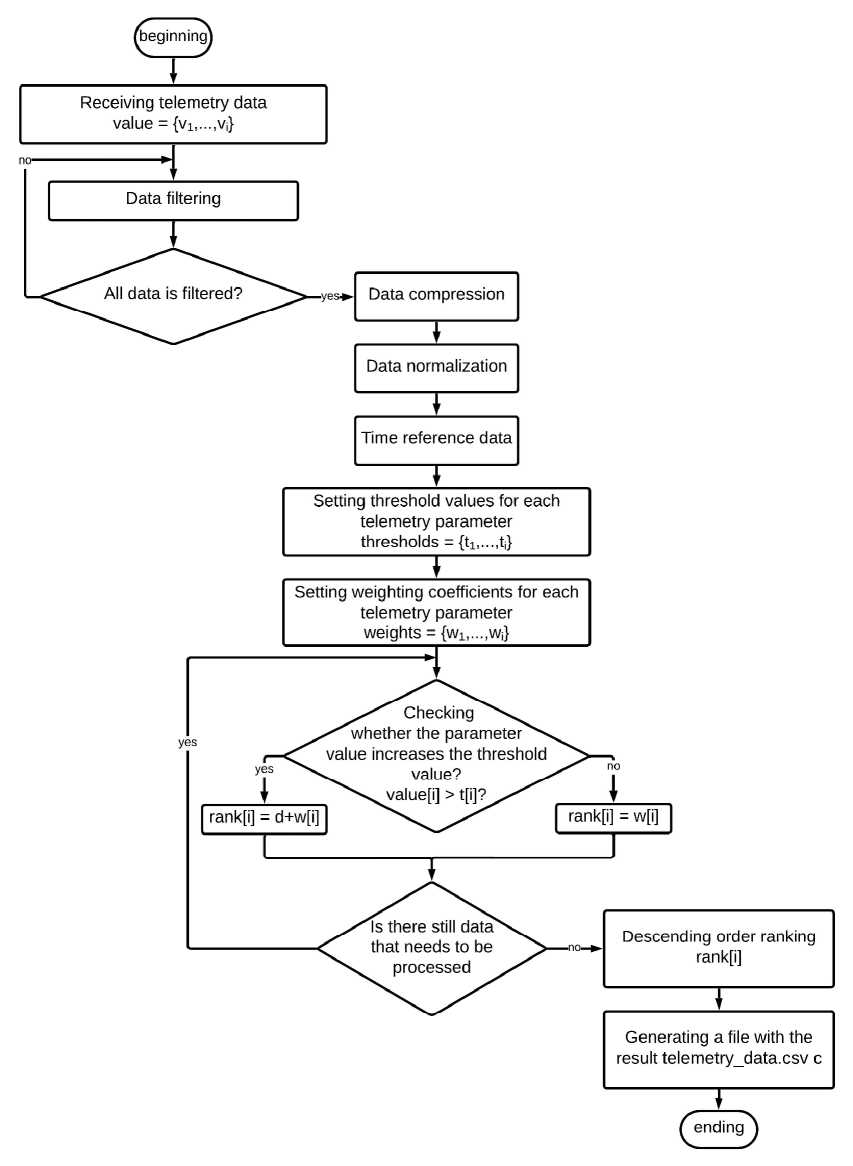
Рис. 4. Алгоритм ранжирования телеметрической информации, поступающей с МКА

• Fig. 4.    Algorithm for ranking CubeSat telemetry

The telemetry data of a spacecraft ranking process involves the following steps:

• 1.    Collecting of telemetry data from small spacecraft (other spacecraft).

• 2.    Pre-processing of data in order to filter out irrelevant or noisy information.

• 3.    Applying a compression algorithm to reduce data size and improve transmission efficiency.

• 4.    Use on-board data processing to analyze and extract features from data.

• 5.    Implementing a machine learning model to identify patterns and anomalies in the data.

• 6.    Developing a rating system based on the priorities of each piece of information.

• 7.    Applying a multi-version approach by developing several versions of the algorithm with different parameters and configurations (Fig. 5).

• 8.    Testing each version of the algorithm on a representative set of telemetry data.

• 9.    Using a rating system to rank the performance of each version algorithm.

• 10.    Selecting of the algorithm with the best performance for each set of telemetry data.

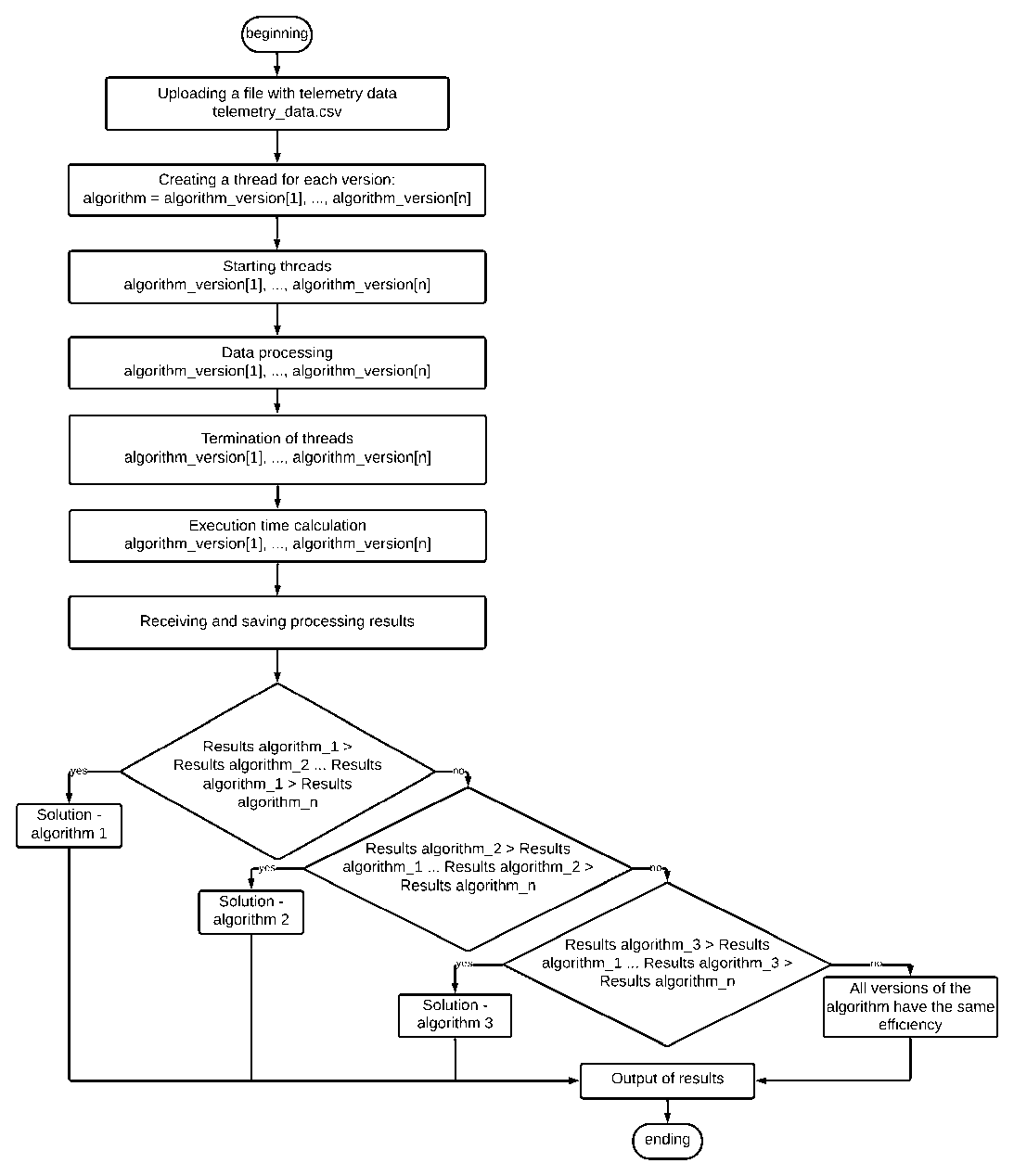
Рис. 5. Введение мультиверсионного подхода в процесс обработки телеметрической информации с МКА

• Fig. 5.    The N-version approach for processing CubeSat telemetry

The ranking algorithm must be flexible and adaptable to different types of telemetry data and processing methods. It should also be able to process data in real time and update the ranking as new data becomes available. Using the MVP approach and ranking system, the algorithm can improve the reliability and accuracy of processing telemetry information from spacecraft.

Multiversion of software for processing telemetry data is a natural course of evolution of these systems. At the same time, the construction of multiversions can be implemented not only within various programming languages, but also in various operating environments, for example Linux.

An important factor contributing to the promotion of Unix platforms to achieve the goals set within the MVP is their accessibility to a wide range of programmers, the availability of open source code and free libraries.

An analysis of the software used in existing nanosatellites has shown that the software architecture of most of the devices is built on the principle of multi-layering, which allows us to propose the introduction of MVP into the components of the software architecture. In the case of the American nanosatellite platform KubOS, multiversion is already built into the concept of its architecture, which uses a combination of two operating systems Linux and U-boot, which perform duplicate functions, thereby creating software redundancy. This approach, which goes beyond the traditional MVP approach, which involves only creating duplicate versions of essentially the same program, suggests the use of conceptually different software as multiversions.

Conclusion

The main problems of reliability formation and characteristic features of software for fault-tolerant control systems are considered. Descriptions of the causes of software failures and methods for ensuring fault tolerance are provided. It is shown that one of the main tasks in the development of small spacecraft control software is the creation of such algorithms and software development methods that can ensure the stability of the entire system against failures .

By applying the methodology of multi-version software development, it is possible not only to ensure a given level of reliability, but also to guarantee the fault tolerance of control and information processing systems. This methodology is based on software redundancy, the introduction of which can significantly increase the level of reliability of the software component .