На пути использования смартфона в качестве гиперспектральной камеры

Гиперспектральная съёмка широко используется в областях, где важно установить физические или химические свойства объектов. В медицине – для определения болезней кожи [1] или органов [2]; в сельском хозяйстве – для оценки состояния растительных культур [3], а также для отделения свежих фруктов и овощей от недозрелых или испорченных [4]; в мусо-ропереработке – для сортировки отходов по химическому составу [5]; в цифровой печати – для калибровки и измерения цвета [6].

Однако камеры, способные снимать гиперспектральные изображения, очень дорогие для широкого применения, поэтому возникает идея использовать другие способы получения таких снимков. Наиболее актуальными в настоящий момент являются методы вычислительной фотографии, задача которых состоит в том, чтобы реконструировать спектры в видимом диапазоне из RGB-изображений [7]. Существует множество алгоритмов для такой спектральной реконструкции. Среди современных решений хорошую точность обеспечивают как классические алгоритмы [8], так и нейросетевые [9, 10].

Вдобавок к упомянутым алгоритмам существуют способы улучшить сами изображения, из которых будет производиться реконструкция, чтобы последняя удавалась точнее. Один из вариантов такого улучше- ния – увеличение количества каналов изображения. Хеллинг и соавторы предложили использовать 7 цветовых узкополосных фильтров [11], чтобы одноканальной камерой осуществлять мультиспектральную съёмку; таким образом, на выходе получалось 7 чёрно-белых фотографий одной сцены, которые объединялись в 7-канальное изображение. Вычислительные эксперименты показали, что средняя цветовая ошибка ΔE94 в данном случае составляет около 0,3 (меньше порога человеческого цветоразличения). В работе [12] Валеро и соавторы снимали одну и ту же сцену трёхканальной камерой сначала без фильтров, а затем поочерёдно с фильтрами из ограниченного набора. Таким образом, при использовании n фильтров получалось (3n + 3)-канальное изображение. Целью работы был поиск наилучшей комбинации для спектральной реконструкции. С увеличением n качество реконструкции улучшалось, но на n =3 авторы остановились, так как решили, что дальше оно существенно улучшаться не будет. В сравнении с реконструкцией по трём каналам у них получилось достичь втрое лучшей точности (по метрике RMSE, нормированной на максимум спектра).

Альтернативно выбору ограниченного набора фильтров из существующих в литературе рассмотрен вопрос проектирования спектральных фильтров «с нуля». Этому посвящена, например, работа Финлейсона и соавторов [13]: там ищется ровно один фильтр, который будет наложен на трёхканальную камеру. Но ставится цель не реконструировать спектры, а сделать камеру более колориметрической, то есть такой, цветовое преобразование координат которой позволит точнее предсказывать отклики стандартного наблюдателя (CIE 1931) на ту же сцену. Авторы показали, что точность предсказания с фильтром в среднем выше в 4 раза, чем без фильтра. Статья Ду-Йонга и соавторов [14] посвящена спектральной реконструкции при помощи съёмки трёхканальной камерой с наложением различных фильтров. Это та же идея, что и у Валеро [12], но функции пропускания фильтров имеют произвольную форму и ищутся математическим моделированием и оптимизацией. Полученные результаты используются для реконструкции некоторого ограниченного множества спектров, а именно спектр-стимулов зубов. Обе работы объединяют ограничения на функции пропускания фильтров – максимум второй производной и вложенность множества значений в отрезок [0; 1]. Первое ограничение авторы вводят как необходимое условие для физической реализуемости фильтров, а второе довольно естественное: фильтры не могут усиливать интенсивность света или делать её отрицательной.

В упомянутых работах есть недостаток: в них не рассматривается никаких методов спектральной реконструкции, кроме линейной регрессии. Этого недостатка лишена работа схожей тематики от Ни и соавторов [15], где при помощи глубокого обучения проектируются сами чувствительности мультиспек-тральной камеры, из снимков которой нейросетевым методом восстанавливаются гиперспектральные изображения.

В отличие от статьи [15] и сходно со статьями [12, 14], в данной работе рассматривается задача проектирования спектральных фильтров для уже существующего набора из 4 камер. Одновременно с этим выбирается алгоритм для наилучшей спектральной реконструкции. Эти два вопроса вместе не рассматривались ни в одной из приведённых статей.

Перспективная задача – сделать гиперспектральную съёмку доступной широкому кругу лиц. На данный момент самая распространённая категория смартфонов имеет четыре близко расположенные камеры: доля таких устройств на рынке превышает 30% [16]. Если изготовить чехол для смартфона, который «накроет» каждую камеру своим фильтром, чувствительности каждой из четырёх камер будут изменены по-своему, и вместо четырёх практически одинаковых 3-канальных сенсоров мы получим четыре различных 3-канальных сенсора. Или, иными словами, один 12-канальный. Это позволит получать 12канальные изображения практически единомоментно. Если установить на телефон программное обеспечение для спектральной реконструкции и решить проблему параллакса (каждая камера видит сцену немно- го под разными ракурсами), то мы получим мобильную гиперспектральную камеру (рис. 1).

Итак, цель данной работы – провести численное моделирование описанной 12-канальной съёмки (без параллакса) и при помощи методов оптимизации подобрать такие функции пропускания фильтров, чтобы восстановление гиперспектральных изображений удавалось наилучшим образом.

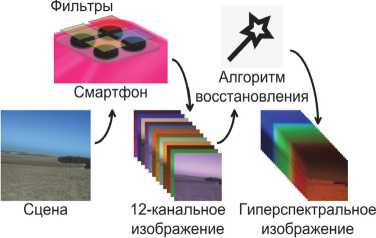
Рис. 1. Предлагаемая схема доступной спектральной реконструкции

Постановка задачи

Заранее отметим, что в данной работе мы будем иметь дело не с изображениями, а с набором пикселей, то есть не будем использовать пространственную информацию. Все спектры будут восстанавливаться независимо друг от друга.

Спектр излучения представим в упрощённом виде – в виде вектора – если зафиксировать диапазон длин волн и шаг дискретизации (например, 400, 410, 420, ..., 730 нм). Пусть { r i } П =1 с К k - набор спектров в таком представлении. RGB-отклики камеры можно симулировать выражением c i = S ' r i , где S' - матрица чувствительности камеры размером 3× k . Но мы применяем 4 камеры и 4 различных фильтра, поэтому S' нужно заменить на S ° ( F ₃ , где матрица S :12* k составлена из спектральных чувствительностей 4 камер, F :4× k – фильтры, (^) 3 – матричный оператор, дублирующий каждую строку 3 раза, ° - поэлементное умножение. Итак, отклики 12-канального сенсора даются выражением

C i =( S ° ( F ) ₃ ) r i . (1)

Из откликов камеры требуется восстановить спектры. Задача некорректна, ведь каждому отклику, вообще говоря, соответствует бесконечное число спектров, которые могли его создать (метамеры). Однако практика показывает, что спектры сцен из окружающего мира покрывают отнюдь не всё k -мерное пространство. Фостер и соавторы [17] в своей работе показали, что спектры натуральных красителей при естественном освещении лежат на маломерном многообразии, а относительная частота метамеров (доля метамерических пар среди всевозможных пар спектров из датасета) обычно не превышает 10 ^{– 4}.

Введём алгоритм восстановления спектра g e : К ¹² ^ К ^k , имеюший какие-то параметры

( 0 1 , 0 2 ,...) T = 0 . Тогда восстановленные спектры выражаются как

Г = g 0 ( C i ) = g 0 (( S ° ( F ) 3 ) r i ).                          (2)

Ставится задача о минимизации s ; =i ii r i - r i ii2

при различных 0 и F . Аналогично предшествующим работам будем учитывать физические ограничения на множество всевозможных фильтров F :

• 1)    ограниченность – диапазон значений элементов вложен в отрезок [0; 1];

• 2)    гладкость – ограниченность «второй производной». В качестве дискретного аналога последней используем разностную схему

f "(x ) «    ( f ( x + h ) + f ( x - h ) - 2 f ( x ))          (3)

h ²

и с помощью строкового преобразования

D =

■ 1	0	0 '
- 2	1	0
1	- 2	0
0	1	0
_ 0	0	1 _

получаем из матрицы фильтров матрицу вторых производных функций пропускания: FD . Значит, можно использовать регуляризационное слагаемое X || FD ||jb , которое поможет удовлетворить требованиям на гладкость функций пропускания.

В реальной жизни c i , подаваемые на вход алгоритму g 0 , - это измерения спектрального сенсора (камеры), то есть данные с погрешностью, с шумом. Чтобы учесть это при оптимизации, добавим шум s i к цветовым откликам c i . Генерировать будем его из нормального распределения. Как будет видно в дальнейшем, такое упрощение поможет нам ускорить оптимизацию.

Итого задача оптимизации фильтров в общем случае ставится так:

n min     SII g0 ((S ° (F )3)ri +Si) - ri 122 +X || FD III.

• ⁰. F      м                                              (5)

• s.t.        F e [0;1] ^4x k

Рис. 2 поможет разобраться с устройством первого слагаемого оптимизационного функционала.

Методы решения

Для решения поставленной задачи требуется рассмотреть два вопроса: создание метода поиска оптимального фильтра и создание методов спектральной реконструкции на основе 12-канального изображения.

Первый вопрос уже почти решён: в (5) все символы понятны, кроме g 0 - он был введён как абстрактный параметризуемый метод спектральной реконструкции. Таким образом, остаётся только вопрос подбора методов спектральной реконструкции, которые, в свою очередь, разделились на два типа: параметризуемые и непараметризуемые. Для решения (5) годятся только параметризуемые, они позволяют одновременную оптимизацию формы фильтра и параметров алгоритма реконструкции. С рассмотрения параметризуемых методов и начнём. Мы попробовали два варианта.

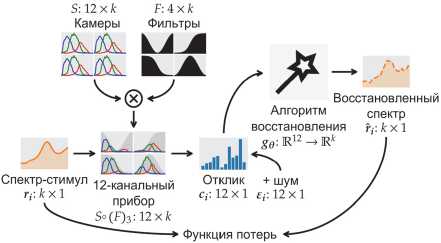
Рис. 2. Схема вычисления первого слагаемого из оптимизационного функционала (5)

• 1.    Линейная регрессия. В задаче проектирования фильтров её часто используют в качестве baseline-решения. Зададим линейное преобразование из откликов в спектры матрицей M : к *12. Тогда r i = M ( c i +s i ). Нахождение в рамках простейшей линейной алгебры позволяет нам проделать несколько трюков.

Во-первых, перепишем первое слагаемое из (5) в вероятностном виде n

S 1 M((S ° (F )3)ri +si)- ri 112 »                    _ i=1                                                                    (6)

« nEr,s | M((S°(F)з)г + s) -r ||2, где случайный вектор r равновероятно принимает значения из {ri },n=1, а s - независимый от r гауссовский случайный вектор с матожиданием 0 и матрицей ковариации a21.

Введя обозначение M ( S ( F ) 3 )- I =A, проделаем преобразования:

E _r , s | M (( S ° ( F ) з ) г + s ) - r | 2 =

= Er,s | M(S°(F)з)г-r + Ms 112 =

= Er,s II Ar + Ms ||2 == Er || Ar 112 +Es || Ms 112 +2Er,s(Ar, Ms) =

= E _r || A r ||2 +E _s tr[ s T M T M s ] + 2 (E _r A r , E _s M s') = (7)

= Er || Ar ||2 + tr[MTMEsssT] + 2(ErAr,MEss) =

= E _r || A r || 2 + tr[ M T M var _s s ] =

= E _r || A r || ₂ ² +c ² tr[ M T M ] =

= Er | Ar |2 +a2 | M |||.

Получается, регуляризация гауссовским шумом на цветовых откликах эквивалентна L2-регуляризации на матрицу M .

Кроме того, можно составить матрицу R : k × n из столбцов r i . Тогда задачу можно записать в следующей нотации:

min     || M ( S ° ( F ) з ) R - R ||| +X || FD |^ +ц || M ||=

^{M , F}                                                     (8)

s.t.       F ∈[0;1]4×k , где µ = nσ2.

Первое слагаемое – самое вычислительно затратное из-за размеров R ( n порядка нескольких миллионов, а k ∼ 30). Используя сингулярное разложение R = U Σ V^T , а также тот факт, что ортогональное преобразование не меняет норму Фробениуса, получим

|| AR |||= || AU S VT |||= | AU S | | ,                  (9)

где для сокращения записи вновь введено A = M ( S ° ( F ) 3 ) – I .

Заметим теперь, что U Σ имеет те же размеры, что и R , однако последние n – k столбцов нулевые и не влияют на значение выражения. Значит, U Σ можно обрезать до размеров k × k . Теперь при подсчёте целевой функции и её градиентов не нужно проводить операции с большой матрицей R . Поскольку в процессе оптимизации R не меняется, сингулярное разложение можно предподсчитать. На практике такой подход позволил ускорить оптимизацию в 100 раз.

Сама оптимизация состоит из чередования двух этапов:

• •    шага градиентного спуска для F при фиксированной M ;

• •    нахождения оптимальной M при фиксированной F (линейная регрессия с L2-регуляризацией).

• 2.    Нейронная сеть. В качестве g θ была опробована полносвязная нейронная сеть с тремя скрытыми слоями размерности 100 и функцией активации LeakyReLU. Вид задачи (5) не меняется, за исключением рассмотрения шума. Чтобы не подстраиваться под его конкретную реализацию, после каждого шага оптимизации ε i перегенерировался.

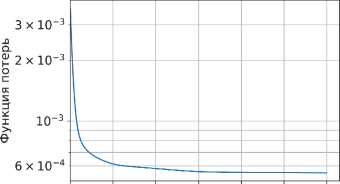
Скорость сходимости оптимизационного процесса можно видеть на рис. 3. Количество необходимых итераций определялось при слежке за изменением фильтров. Как только фильтры переставали изменяться, процесс останавливался.

0   2500 5000 7500 10000 12500 15000

Номер итерации

Pис. 3. Динамика изменения функции потерь из (8) при использовании оптимизатора Adam

Введение регуляризации на гладкость (параметр λ ) было заимствовано из литературы [14]; однако в ней не даются какие-либо рекомендуемые значения. Поэтому пришлось обойтись подбиранием λ «на глаз». Слишком малые значения не оказывали достаточного влияния на гладкость. Слишком большие приводили к тому, что множество значений функций пропускания покрывало не весь отрезок [0; 1]. Все результаты в данной статье получены при λ = n ^0,0016.

Для обоих вариантов g θ использовался оптимизатор Adam из пакета PyTorch, хорошо зарекомендовавший себя для невыпуклых задач. Он не поддерживает оптимизацию с ограничениями, поэтому после каждого шага отрицательные элементы матрицы F занулялись, а превосходящие единицу заменялись на 1.

Если зафиксировать F , то можно будет рассматривать не только параметризуемые алгоритмы восстановления. В данной работе в качестве такого фиксированного F детально рассматривается результат оптимизации фильтров при линейно-регрессионной g θ (нейросетевой вариант рассмотрен отдельно). А также добавлены некоторые baseline-решения для F :

• 1.    Пусть у каждого фильтра будет три пика в красной, зелёной и синей зонах видимого спектра соответственно. Эти пики подберём вручную так, чтобы чувствительность каждого из 12 каналов полученного сенсора имела характерный пик в какой-то своей длине волны (см. рис. 4).

• 2.    Сгенерируем элементы F из нормального распределения со средним 0,5 и дисперсией 0,1².

• 3.    Все элементы F равны 1 (эквивалент отсутствия фильтров).

Каждый набор фильтров F будет иметь своё кодовое обозначение. Фильтры, полученные при помощи линейной регрессии, будут именоваться Regression-trained , а при помощи нейронной сети – FCN-trained . Baseline-фильтры из предыдущего параграфа назовём Manual , Random и None соответственно.

Сравнение «натренированных» фильтров с baseline-решениями поможет понять оправданность нашего вычислительного подхода к подбору фильтров.

Как только матрица F зафиксирована, постановка задачи становится классической, и выбор методов реконструкции практически не ограничен. Главное, чтобы метод можно было адаптировать под восстановление из 12-мерных цветовых откликов, а не из 3-мерных. В работе рассмотрены следующие алгоритмы восстановления:

• 1.    Линейная регрессия. Уже была описана при постановке задачи (8).

• 2.    A+. Алгоритм, предложенный Ву и соавторами [8], основанный на разреженном кодировании данных и представлении каждого исходного спектра линейной комбинацией из предпосчитанного словаря.

• 3.    FCN. Полносвязная нейронная сеть. Уже была описана сразу после линейной регрессии.

• 4.    Kernel FCN. Данный метод основан на работе Финлэйсона и соавторов [18]. В ней предлагается

идея, позволяющая из алгоритмов спектральной реконструкции делать такие, которые предсказывают спектр с нулевой цветовой ошибкой. Идея состоит в следующем. Камеру можно рассмотреть как линейное преобразование из пространства спектров в пространство цветов. Разобьём спектральное пространство на ядро преобразования и дополнение к нему. Теперь восстановление спектра будет заключаться в восстановлении каждой из компонент из этих подпространств. Компонента не из ядра восстанавливается аналитически. А для восстановления компоненты из ядра будем использовать привычные алгоритмы спектральной реконструкции. В качестве такого мы взяли полносвязную сеть из предыдущего пункта.

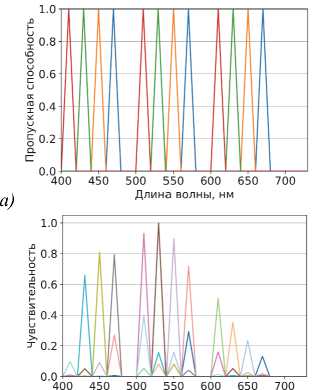
Длина волны, нм

б)

Pис. 4. Пропускные способности Manual-фильтров (а) и чувствительности соответствующего 12-канального спектрального сенсора (б)

Оценка качества

После обучения алгоритмов нужно проверить их точность на тестовой части набора данных. Встаёт вопрос о выборе метрик качества. В исключительно прикладном исследовании конечная метрика должна быть проблемо-ориентированной: например, если целевая задача – угадывать цвет красителя, то метрика должна быть цветовой. В нашем случае целей для восстановления спектра множество, поэтому предстоит абстрактно оценивать отличие восстановленных спектров от исходных. В таком случае от метрики ожидаются следующие свойства:

• 1.    Интерпретируемость. Возможность интуитивно понять, большая величина получилась или маленькая.

• 2.    Практичность. Удобство в сравнении с другими исследованиями, а также в использовании для оценок точностей при решении разных конкретных задач. Например, если известно значение метрики восстановления спектра, какой будет метрика восстановления цвета?

С учётом сказанного мы ввели следующую метрику качества восстановления спектров:

NSE ( R , J R ) =¹ У ¹ r i r i ^{1 1} .

n i=i II ri 11

Данная метрика призвана решить проблему интерпретируемости. По сути, это площадь разности спектров, нормированная на площадь исходного. Такую величину можно измерять в процентах.

Также были выбраны ещё две метрики:

RMSE ( R , R )

n

= К У I ri - ri I nk i=1

2 2 ,

MangE ( R , R )

ⁿ = ¹ ∑ n i =1

arccos

〈 r i , r ˆ i 〉

I r i 121 r i 112

RMSE является популярной метрикой качества восстановления спектра (например, ею оценивались решения крупнейшего соревнования по спектральному восстановлению [7]). По своей сути это среднеквадратичное отклонение, приходящееся на длину волны. По значению этой метрики можно приблизительно выразить, насколько два спектра могут отличаться между собой. Но интуитивно представить себе эту метрику сложно (допустим, получилось 0,0025 – это много или мало?).

Другая распространённая метрика — MangE. Она характеризуется тем, что оценивает отличие форм спектров, то есть не штрафует, если предсказатель ошибся только в интенсивности. Однако проблема интепретируемости по-прежнему присутствует, поскольку речь идёт об углах в многомерном пространстве.

Эксперименты

Источники данных. Ли и соавторы [19] в 2021 году представили набор данных из 409 гиперспектральных indoor- и outdoor-изображений разрешения 512×512 с 34 спектральными каналами от 400 до 730 нм с шагом 10 нм. Он содержит не спектры-стимулы, а приблизительные отражательные способности объектов в сцене. Это позволяет симулировать новые гиперспектральные изображения тех же сцен, но под другими источниками света. Таким образом, мы из 409 изображений получили 1636, используя для каждой картинки 4 стандартных источника: A18, F2, D65, E [20] (рис. 5).

Все пиксели набора не уместятся в оперативную память, поэтому из каждой картинки пиксели брались с шагом 12 по горизонтали и вертикали. Разделение на тренировочную и тестовую части бралось в отношении 4:1.

Чтобы проверить полученные фильтры на «пере-обучённость», был добавлен второй тестировочный набор данных — NTIRE2020 [7]. Он содержит 450 outdoor-изображений разрешения 512×482 с 31 спек- тральным каналом (от 400 до 700 нм). На этот раз даны именно спектральные освещённости сенсора. Таким образом, набор содержит более однообразные данные, и именно поэтому был выбран в качестве тестового, а не тренировочного. По аналогии с набором данных Li для экономии оперативной памяти пиксели брались из сетки с шагом 7.

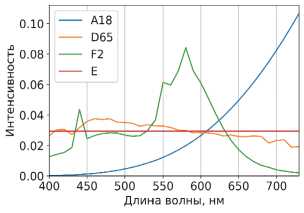
Рис. 5. Интенсивности использованных источников освещения

Для симуляции работы каждой из 4 камер использовались одни и те же чувствительности Canon 60D (рис. 6) [21].

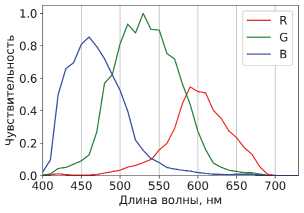
Pис. 6. Спектральные чувствительности камеры Canon 60D

Детали экспериментов. При подборе Regressiontrained -фильтров шум на цветовых откликах предполагался гауссовским, поскольку это помогало ускорить оптимизацию. Во всех остальных случаях (подбор FCN-trained -фильтров, обучение алгоритмов восстановления) было решено прибегнуть к более реалистичному моделированию. Камера являет собой по сути детектор фотонов, поэтому шум будет иметь две составляющие: независимую от уровня сигнала гауссовскую и зависимую от уровня сигнала пуассоновскую [22]. Вторую составляющую мы приближаем гауссовской случайной величиной с дисперсией, пропорциональной величине исходного сигнала.

Полностью все шаги численных экспериментов выглядят так:

• 1.    Инициализация Manual -, Random - и None -фильтров.

• 2.    Нахождение Regression-trained -фильтров путём решения (8).

• 3.    Генерация откликов камеры для всех видов фильтров вместе с гауссовским шумом.

• 4.    Обучение алгоритмов восстановления на полученных парах «отклик – спектр».

• 5.    Оценивание всех обученных алгоритмов на тестовой части датасета Li и на датасете NTIRE2020, подбор гиперпараметров.

Особняком стоял эксперимент с нахождением FCN-trained -фильтров путём обучения одновременно с сетью согласно задаче (5) и оцениванием полученной нейросети и фильтров на тех же датасетах.

Результаты

Фильтры, полученные в результате оптимизации (5) и (8), изображены на рис. 7 и 8.

а)

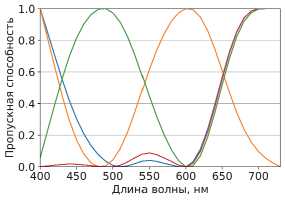
б)

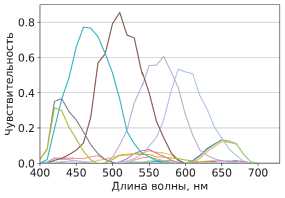
Pис. 7. Пропускные способности Regression-trained-фильтров (a) и чувствительности соответствующего 12канального спектрального сенсора (б)

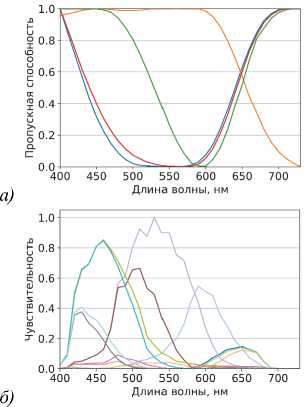
Pис. 8. Пропускные способности FCN-trained-фильтров (a) и чувствительности соответствующего 12-канального спектрального сенсора (б)

Результаты измерения всех трёх метрик на тестовых наборах данных представлены в табл. 1, 2 и 3.

Напомним, что FCN-trained -фильтры проверялись только в сочетании с алгоритмом восстановления FCN. Результат измерения метрик в этом случае представлен в табл. 4.

Табл. 4. Метрики для FCN-trained-фильтров

	MangE	NSE	RMSE
Li (тест)	19,23	22,1 %	0,0049
NTIRE	6,34	6,5%	0,0220

Табл. 1. Метрика NSE

		Regression-trained	Manual	Random	None
4* Li (тест)	Регрессия	23,3 %	35,6%	34,3 %	31,4%
	А+	19,8%	29,3%	28,5 %	26,5%
	FCN	18,1 %	26,4 %	23,2 %	21,1 %
	FCN kernel	97,7 %	35,8%	78,5 %	22,1 %
4* NTIRE	Регрессия	6,9%	9,3 %	16,3 %	16,9 %
	А+	6,0 %	9,7%	21,2 %	21,7%
	FCN	6,4%	10,1 %	25,1 %	28,2%
	FCN kernel	90,2%	10,9%	50,6 %	26,1 %

Табл. 2. Метрика MangE

		Regression-trained	Manual	Random	None
4* Li (тест)	Регрессия	20,87	27,53	25,94	24,02
	А+	18,44	22,99	23,26	22,25
	FCN	16,14	20,27	18,79	17,54
	FCN kernel	64,63	31,41	50,75	17,96
4* NTIRE	Регрессия	6,77	8,82	13,37	13,71
	А+	6,01	8,24	15,82	16,20
	FCN	5,86	8,08	15,93	17,18
	FCN kernel	53,17	13,50	37,12	16,31

Табл. 3. Метрика RMSE

		Regression-trained	Manual	Random	None
4* Li (тест)	Регрессия	0,0049	0,0067	0,0071	0,0067
	А+	0,0047	0,0061	0,0064	0,0063
	FCN	0,0045	0,0056	0,0058	0,0056
	FCN kernel	0,1282	0,0074	0,0193	0,0056
4* NTIRE	Регрессия	0,0228	0,0279	0,0504	0,0532
	А+	0,0202	0,0297	0,0719	0,0729
	FCN	0,0210	0,0307	0,0870	0,0967
	FCN kernel	0,5776	0,0366	0,1335	0,0902

Как видно, Regression-trained -фильтры показывают наилучшие результаты на каждом наборе данных. В сравнении с None -фильтрами, на датасете NTIRE удалось улучшить все метрики по меньшей мере в 3 раза. Наилучший алгоритм восстановления однозначно выбрать нельзя: на наборе данных Li лучше показывает себя FCN, а на NTIRE – алгоритм A+.

Любопытна форма чувствительностей полученного 12-канального сенсора (рис. 7). Она во многом следует принципу построения Manual -фильтров: каждая чувствительность имеет один пик, и все пики разные и почти равномерно распределены по видимому диапазону. Это значит, что при сочинении Manual -фильтров был найден правильный принцип и интуиция сработала хорошо.

Тем не менее, сами Manual-фильтры показывают в среднем самые худшие результаты. Это влияние шума: цветовые отклики при использовании Manual-фильтров оказываются малыми из-за маленькой интенсивности пропускания фильтров, а значит, они больше подвержены негативному влиянию шума. Таким образом, неявно при поиске оптимальной формы фильтров с учетом зашумления учитывается и квантовая эффективность сенсора.

В целом можно сделать вывод, что на датасете Li фильтры расположились по качеству в порядке Trained >  None >  Random >  Manual , а на датасете NTIRE: Trained >  Manual >  Random >  None .

Заметим также, насколько неожиданно плохо работает алгоритм FCN-kernel. По своей задумке он должен был быть улучшенной версией FCN, однако показывает результаты намного хуже. Изучив, почему так происходит, мы обнаружили, что, если тестировать алгоритмы на бесшумных данных, результаты у FCN-kernel немного лучше, чем у FCN. Дело в том, что в случае FCN-kernel нейросеть учится восстанавливать составляющую спектра из подпространства – ядра преобразования 12-канального сенсора. Составляющая из дополнения к подпространству вычисляется аналитически: домножением на линейный оператор. Именно вторая составляющая и вносит негативный вклад в правильность восстановления спектра. Нейросеть была обучена на шумных данных, а линейный оператор – нет.

Интересно, что полносвязная сеть в сочетании с фильтрами, обученными под себя (FCN-trained), по- казала результаты хуже, чем в сочетании с регрессионными фильтрами. По-видимому, при обучении сети одновременно с фильтрами мы имеем дело с задачей с большим количеством локальных минимумов, которые не дают нам найти глобальное решение. Также бросается в глаза чрезмерная гладокость FCN-trained-фильтров (рис. 8). Из-за того, что функция потерь и гладкостная регуляризация – два слагаемых одного и того же оптимизационного функционала, оптимизатору Adam оказалось проще разгладить фильтры, чем уменьшать функцию потерь.

Заключение

Была рассмотрена задача восстановления гиперспектральных изображений из 12-канальных, которые, в свою очередь, были получены путём комбинирования 3-канальных изображений с 4 камер, на которые было наложено 4 разных фильтра. Математическая формулировка этой задачи позволила нам спроектировать фильтры и подобрать алгоритм восстановления так, что качество спектральной реконструкции улучшилось в три раза в сравнении с реконструкцией по обыкновенным 3-канальным изображениям. Процесс оптимизации фильтров был ускорен при помощи ряда математических приёмов. Было показано, что оптимизация фильтров позволяет добиться лучших результатов, чем проектирование фильтров интуитивно.

Также был выявлен недостаток идеи статьи Фин-лэйсона и соавторов [18]. Авторы работы не учитывали существенное влияние шума сигнала на точность восстановления спектра, что, как показывает практика, является важнейшим фактором. В связи с этим, мы предлагаем определять алгоритм восстановления спектра не как функцию, принимающую на вход цветовой отклик, а как функцию, принимающую на вход вероятностное распределение на пространстве цветовых откликов.

Дальнейшая работа будет нацелена на приближение условий вычислительного эксперимента к реальным. Требуется рассмотреть алгоритмы восстановления спектра, учитывающие пространственную информацию. Именно такие алгоритмы являются в настоящий момент state-of-the-art; к тому же они помогут нивелировать влияние шума в цветовых откликах, ведь соседние пиксели изображения будут иметь схожие средние значения. Планируется исследование вопроса прироста точности восстановления (в том числе спектров окрасок) от числа используемых камер, а также вопроса достижимой точности восстановления для различных уровней шума и битностей сенсоров. Отдельно большое внимание будет уделено задаче дальнейшей формализации требований к физически реализуемым фильтрам с учетом ограничений на точность восстановления сигнала и стоимость изготовления.