Наблюдатель упругого момента двухмассовой электромеханической системы

Анализ поломок механического оборудования клетей прокатных станов показывает, что наиболее вероятными причинами поломок являются разовые либо накопленные циклы перегрузок по крутильному моменту [1, 2]. Прокатные клети работают в режиме периодически повторяющихся ударных нагрузок, обусловленных захватом раската (промежуточного продукта между заготовкой и готовым прокатом) валками. Поэтому целесообразно использовать параметры переходных процессов в диагностических целях.

Высокой информативностью обладает упругий момент в линии привода. Однако системы прямого измерения упругого момента на основе физических датчиков сложны в изготовлении и в агрессивной среде стана горячей прокатки имеют низкий эксплуатационный ресурс. Это подтверждает опыт эксплуатации (недолгий) системы измерения упругой деформации MANNER TG28TE, изготовленной фирмой Manner (Германия), которая была смонтирована на стане 5000 ПАО «Маг- нитогорский металлургический комбинат» в 2011 г. В настоящее время на стане эксплуатируется система измерения упругого момента фирмы SMS group. Она также не является надежным устройством. Причинами низкой долговечности являются тяжелые условия эксплуатации и плановые замены шпинделей, после которых возникают сложности с повторной установкой измерительных (токосъемных) устройств. Положительным результатом внедрения этой системы является то, что она обеспечила возможность проверки адекватности сигналов, поступающих от разработанного наблюдателя упругого момента на шпинделе (информация о наблюдателе и пример его применения для анализа аварийного режима приводится ниже).

Альтернативой прямому измерению упругого момента является его вычисление (восстановление) с помощью наблюдателей, по сути, цифровых теней физической системы [3]. Согласно определению, данному в [4], «наблюдатель состояния – это модель, подключенная параллельно объекту управления и получающая непрерывную информа- цию об изменениях регулирующего воздействия и регулируемой координаты». Разработка наблюдателей параметров двух- и трехмассовых электромеханических систем, которые обеспечивают восстановление момента вала и скорости неприводной массы по параметрам электропривода, является актуальной задачей. В отечественной практике ее решением занимаются представители научной школы Ивановского государственного энергетического университета под руководством профессоров А.Р. Колганова и С.К. Лебедева [5, 6]. В числе зарубежных публикаций, посвященных данной проблематике, следует выделить статьи [7–9].

Разработке цифрового наблюдателя упругого момента двухмассовой электромеханической системы посвящены авторские публикации [10–12]. Рассмотрен наблюдатель упругого момента приводного вала (шпинделя) и скорости валка клети толстолистового стана. Представлены результаты его опытно-промышленных испытаний в электроприводах клети стана 5000. В работах [11, 12] представлены результаты исследований системы автоматического регулирования упругого момента, разработанной на основе этого наблюдателя. Представление главной линии прокатной клети с индивидуальным электроприводом в виде двухмассовой системы с упругим валом и зазором в шпиндельных соединениях обосновано в [13]. В этой же статье рассмотрена методика экспериментального определения параметров двухмассовой системы.

Недостатком этой разработки, безусловно, заслуживающей внимания, является то, что восстановление упругого момента выполняется путем дифференцирования сигнала разности измеренной скорости двигателя и вычисленной скорости второй массы двухмассовой системы. Как известно,

операция дифференцирования снижает помехозащищенность и тем самым отрицательно влияет на достоверность восстанавливаемого сигнала. Стремление исключить данную процедуру и максимально упростить восстановление упругого момента привело к разработке более простого цифрового наблюдателя, который рассматривается ниже. Как и в предыдущих случаях, исследование выполняется на примере электропривода горизонтальной клети стана 5000.

Разработка наблюдателя упругого момента двухмассовой системы

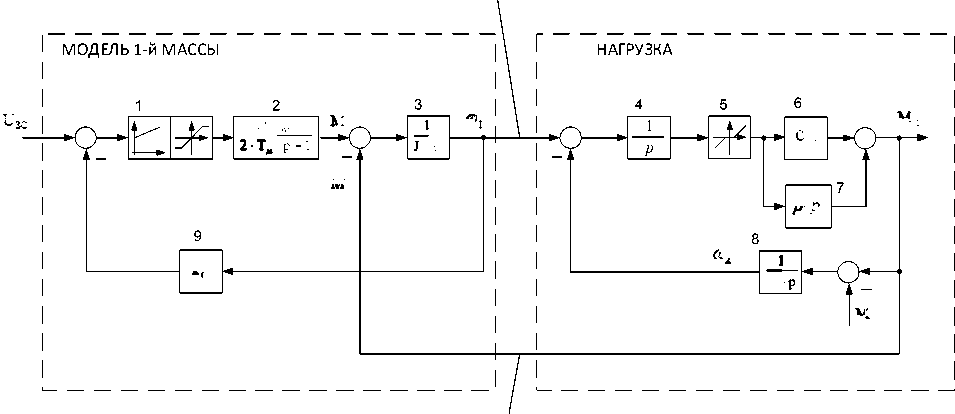
Структура наблюдателя. Двухмассовая система «электропривод – валок» может быть представлена в виде замкнутой двухконтурной структуры, представленной на рис. 1. Параметры модели, рассчитанные по упомянутой методике [13], представлены в табл. 1. На схеме обозначены: Т _µ – постоянная времени контура момента; ω₁, ω₂ – скорости первой и второй масс. Расшифровка остальных параметров приведена в табл. 1.

Для представленной структуры справедлива система дифференциальных уравнений, обоснованная в [10]:

dM ^ dt

—

—Мг +

Т_т  ¹

dtoi      1 _ ,

—- = -Мл dt     J-   1

—

т к  M1ref

^Тт ^ оМ

7М12 ;

— = С _2Ю1 - С ₂ю₂ + ^ М, - в ^J-^M₁₂ + ^ М_с; dt ^{12 1      12 2}    J -    ¹ Р j - ^j₂    ¹²     j ₂ с.

drn₂ dt

= уМ 12 -уМ с . ^J 2            ^J 2

При разработке учитывается, что момент, обусловленный трением, незначителен, соответственно блок 7 может быть исключен из схемы. Принимается, что для этой структуры нагрузка

СКОРОСТЬ 1-й МАССЫ

МОМЕНТ «НАГРУЗКИ»

Рис. 1. Структура модели, поясняющая разработку наблюдателя

Fig. 1. The structure of the model explaining the development of the observer

Таблица 1

Параметры модели двухмассовой системы клети стана 5000

Table 1

Parameters of the model of the two-mass system of the mill 5000 crate

Параметр Обозначение Размерность Значение Момент инерции первой движущейся массы (двигателя) J1 кг·м2 125 000 Момент инерции второй движущейся массы (валка) J2 кг·м2 114 571 Жесткость упругой связи С12 Н·м/рад. 5 934 842 Собственная частота упругих колебаний ω12 рад/с 9,96 Ускорение электропривода ε0 рад/с2 1–3 Зазор в передаче (блок 5) δ град. 1–3 Средний упругий момент M12 МН·м 1,9 Коэффициент демпфирования (типа, вязкое трение) β – 2,817 Декремент затухания ξ – 0,172 Коэффициент усиления регулятора скорости (блок 1 на рис. 1) рс – 19,5 Постоянная времени регулятора скорости г рс с 0,0041 представляет собой «черный ящик». Ее воздействие на модель 1-й массы передается через упругий момент шпинделя. Идея заключается в том, что при этих условиях можно реализовать наблюдатель упругого момента аналогично наблюдателю нагрузки одномассовой системы. Для этого может быть применена схема без вычисления производных скорости. Структура разработанного наблюдателя представлена на рис. 2а.

Для расчета момента нагрузки используется специальный регулятор компенсации рассогласования скоростей (далее – регулятор автонастройки). Выполнена его автоматическая настройка по методу Циглера – Николса [14]. В базовой публикации [15] упомянуто, что « настройка конечного цикла Циглера – Николса или настройка с обратной связью широко известна как довольно точный эвристический метод для определения оптималь-

Скорость двигателя

Момент двигателя

м Из мер.

Момент на

шпинделе

a)

b)

c)

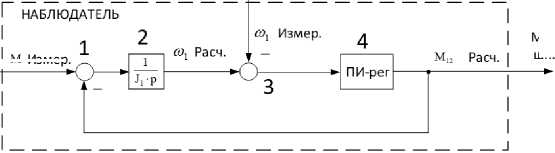
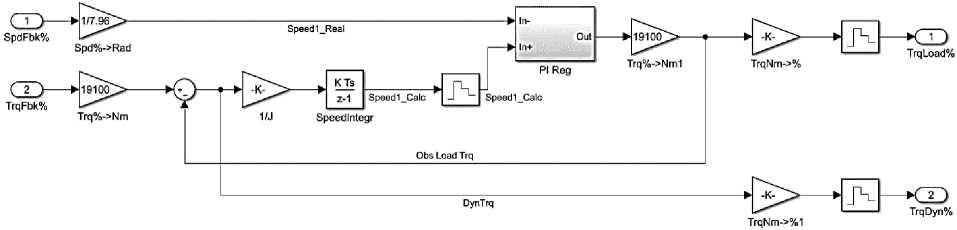
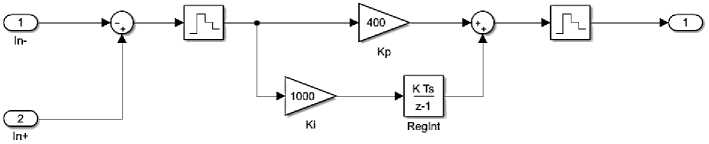
Рис. 2. Схема наблюдателя (а), ее реализация в MATLAB Simulink (b) и дискретная модель ПИ-регулятора автонастройки (c)

Fig. 2. Observer diagram (a), its implementation in MATLAB Simulink (b) and a discrete model of the PI auto-tuning controller (c)

Таблица 2

Параметры наблюдателя упругого момента

Parameters of the torque observer

Table 2

Параметр Значение Ед. измерения Номинальная скорость двигателя 7,96 рад/с Номинальный момент двигателя 1 910 000 Н·м Момент инерции двигателя 1 250 000 Н·м2 Коэффициент П-части регулятора автонастройки 400 – Коэффициент И-части регулятора автонастройки 1000 – ных настроек ПИД- и ПИ-регуляторов для широкого круга распространенных промышленных процессов». Методика автонастройки регуляторов на микроконтроллере изложена в [16]. Параметры регулятора приведены в табл. 2.

Этот регулятор «вычисляет» момент нагрузки первой массы и стремится «привести в ноль» разницу между измеренной и расчетной скоростями. Динамический момент в модели рассчитывается как разница между полным моментом двигателя, полученным из САР преобразователя частоты, и моментом нагрузки, полученным наблюдателем. Затем динамический момент интегрируется с коэффициентом (1/ J 1 ), таким образом вычисляется скорость 1-й массы.

На рис. 2b приведена структура наблюдателя в MATLAB Simulink. Она составлена по системе дифференциальных уравнений, приведенной выше. Регулятор автонастройки (рис. 2c) представляет собой обычный ПИ-регулятор и должен обладать достаточным быстродействием для минимизации ошибок расчета. Как видно, в структуре наблюдателя операция дифференцирования заменена процедурой интегрирования, что повышает помехозащищенность сигнала. Это является преимуществом по сравнению с известными техническими решениями. Вторым преимуществом является простота настройки. Недостатком, по сравнению с разработкой [10, 12], является то, что не восстанавливается сигнал скорости второй массы. Такой сигнал может быть необходим при разработке замкнутой системы регулирования упругого момента [11]. Однако такая задача в представленной публикации не рассматривается. Выделение сигнала скорости может быть выполнено в ходе дальнейших исследований.

Следует отметить, что в рассмотренном случае выполнена виртуальная настройка наблюдателя, при которой после отработки в MATLAB Simulink алгоритм наблюдателя был импортирован в программное обеспечение (ПО) промышленного контроллера. В результате осуществлен виртуальный ввод наблюдателя в работу. Для электроприводов исследуемого стана такой подход является обоснованным и достаточным. С целью обобщения результатов и рекомендаций по использованию наблюдателя на других объектах, целесообразно представить методику расчета параметров регулятора автонастройки. Однако этот материал достаточно объемный, поэтому может быть изложен в отдельной публикации.

Экспериментальные исследования

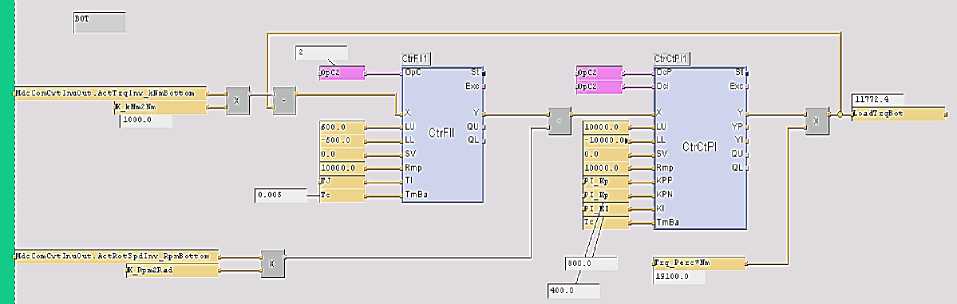
Программная структура наблюдателя, выполняющая вычисления для одного электропривода, приведена на рис. 3а. Она соответствует схеме, показанной на рис. 2а, и включает в себя последовательно соединенные блоки вычитания, интегратора расчетной скорости (CtrFull), вычитания сигнала расчетной скорости из сигнала измеренной скорости и ПИ-регулятора (CtrCTPi). На рис. 3b показана структура (бит) ограничения нагрузки по моменту для аварийных случаев. Установлены пороговые значения: 6500 кН·м – для предупреждения и 8000 кН·м – для торможения быстрым остановом.

Проверка адекватности вычисления упругого момента. При оценке адекватности восстанавливаемых величин, поступающих от наблюдателя, предложен подход, согласно которому осуществляется импорт сигналов скорости и момента двигателя в модель наблюдателя (см. рис. 2b). Они могут быть измерены заранее и сохранены в виде массивов либо подаваться на входы наблюдателя в онлайн-режиме. Здесь используются предварительно записанные сигналы, импортированные в MATLAB из информационно-измерительной системы IBA PDA. Такой подход получил название «квазиэкспериментального», в отличие от экспериментального анализа, когда сигналы поступают в виртуальную систему непосредственно после измерения. В [17] отмечается, что « этот подход обеспечивает баланс между преимуществами для практиков и методологической строгостью. Хотя эта процедура делает исследование неполным контролируемым экспериментом, часто удается сохранить характеристики квазиэксперимента ». Данный термин также используется в публикациях [18–20].

Проверка адекватности выполняется на примере анализа динамических режимов. Предлагается методика, согласно которой выполняются следующие действия.

• 1.    Данные, сохраненные в виде массивов, импортируются в MATLAB, где подаются на вход дискретной модели.

  

  а)

  
  
  

  b)

  Рис. 3. Экранные формы ПО контроллера управления, реализующие алгоритмы наблюдателя (а) и ограничения нагрузки по моменту в аварийных режимах (b)

  Fig. 3. On-screen forms of the control controller software implementing observer algorithms (a) and load limits in emergency modes (b)

  
  

• 2.    В ыпол н яет ся м одел иро в а н ие проц ес с ов , р а н ее з а фиксиров а н ных на ос ци л л огра м м а х .

• 3.    В ыпол н яет ся с опос та вл ение осци л л огра м м с р а с че тным и з а в исим ос тя м и м е тодом их с ов м ещ е н ия либ о м е тодом с ра вне н ия координат в х арактерных точках.

• 4.    Дл я оц ен к и достов е рнос т и м ог у т быть приме не ны м е тоды с татистиче ской обра ботк и ре зу льтатов (здесь не приводятся).

Динамические режимы электропривода. Н а рис . 4а пре дс тав л ены ос ци л л огра м м ы пос л ед ов ате л ь ны х у с коре н ия и з а ме дл ени я эл ектропри в ода . Этот р е жим явл яе тся наи бол е е и нформ а тивным с точки з ре ни я оценк и а дек в а тнос т и на б л ю да те ля, так ка к прояв ляются не лин е йные с в ойств а объ е кта, обусловленные наличием за з оров в шпин де льных с ое ди нени ях . В ре ж им е ра з гона проис х одит гара нти ров анное за м ыка н ие з а з ора , в ре ж им е торможения – его ра з м ыка ние . На рис . 4b представлены ан ало г и ч н ы е о сц и л ло г р ам мы , з аф и кси р о ва нны е в р ежи ме у д ар н о г о п р ило жен и я н агру зки п р и входе металл а в клет ь . М о мен т д ви г ателя М дв ( окн о 2) сра з у пос л е з ах в а т а дос тига е т уровня о граничения 240 % ном инал ь н ого з на чен ия.

Зависимости моментов на шпинделе – измеренного системой PDA Мш(измер) и восстановленного наблюдателем Мш(восст) – на рис. 4а, b полностью совпадают. Кривая Мш(восст) момента с наблюдателя находится на фоне кривой Мш(измер) момента, поступающего от физической измерительной систе- мы, поэтому в черно-белой печати становится незаметной. Это позволяет сделать вывод, что, несмотря на влияние нелинейности, обусловленной зазором, восстановление сигнала наблюдателем обеспечивается с абсолютной точностью.

Нелинейные свойства электромеханической системы с зазором не могут быть описаны аналитически. Однако представленные осциллограммы позволяют утверждать, что предложенный принцип обработки измеренных сигналов при правильной настройке регулятора автонастройки позволяет максимально приблизить восстановленные сигналы к физическим. При этом автоматически обеспечивается учет нелинейных свойств объекта. Необходимости в проведении сравнительного анализа процессов с использованием математических методов нет, так как кривые переходных процессов абсолютно совпадают.

Сделанные выводы подтверждены результатами исследований различных режимов электроприводов клети. Проведен уникальный анализ динамических моментов, возникающих на шпинделях в аварийных режимах, в том числе сопровождающихся поломками оборудования. Возможность таких исследований обеспечена применением предложенного квазиэкспериментального подхода. Следует отметить, что подобные исследования в литературных источниках не встречаются. В качестве примера ниже представлен краткий анализ аварийной ситуации.

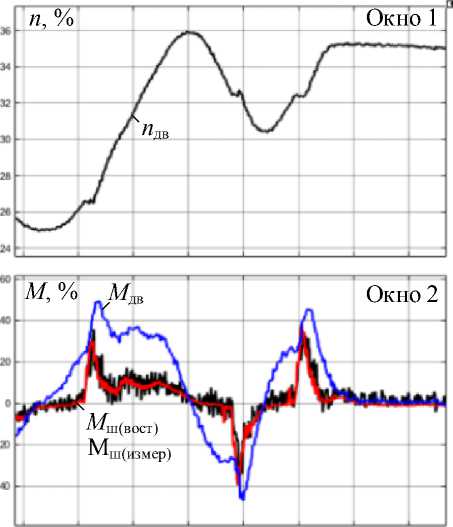
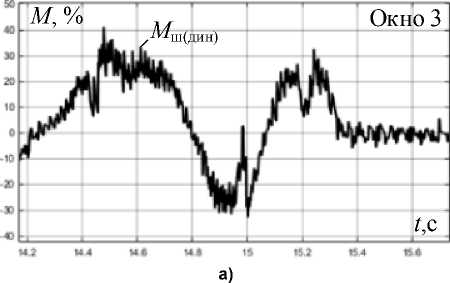
Рис. 4. Осциллограммы при последовательном ускорении и замедлении электропривода (а) и в режиме захвата металла валками (b): n _дв – скорость двигателя, % номинальной; M _дв – момент двигателя; M _ш ( _измер ) – момент на шпинделе от датчика; M _ш ( _восст ) – момент с наблюдателя; M _ш ( _дин ) – динамический момент с наблюдателя

Fig. 4. Oscillograms with sequential acceleration and deceleration of the electric drive (a) and in the mode of metal capture by rolls (b): n дв – motor speed, % nominal; M дв – motor torque; M ш(измер) – torque on the spindle from the sensor; M _ш ( _восст ) – torque from the observer; M _ш ( _дин ) – dynamic moment from the observer

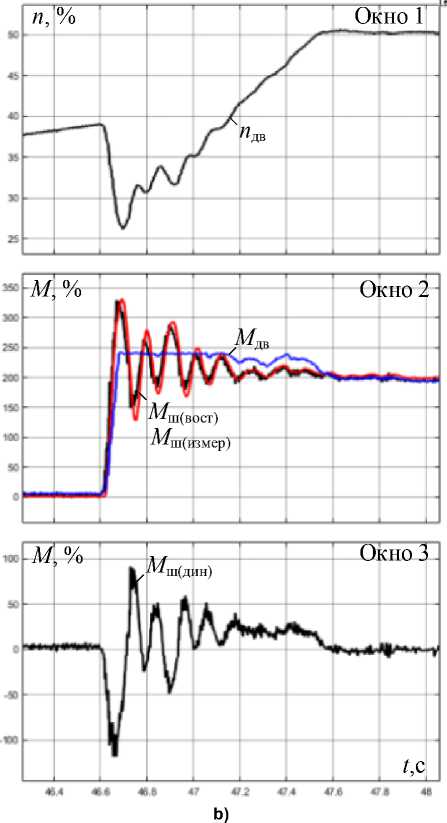
Анализ аварийного отключения во время прокатки. Рассматривается случай аварийного отключения электроприводов во время прокатки, вызвавшего останов клети с металлом в валках. В этом конкретном случае не произошло поломок валков либо элементов шпиндельных соединений, поэтому анализ динамических нагрузок носит информативный характер. Полученная информация может быть использована при настройке системы аварийного торможения двигателей. Осциллограммы, полученные в данном режиме, представлены на рис. 5. В результате аварии скорости n _НГП, n _ВГП (окно 1) и моменты М _НГП, М _ВГП (окно 2) двигателей снизились до нулевых значений с небольшой разницей во времени. Индекс «ВГП» означает принадлежность сигнала к главному электроприводу верхнего валка, индекс «НГП» – к электроприводу нижнего валка.

Поставлена задача оценки упругого момента на шпинделях для этого режима. С этой целью предварительно записанные сигналы в виде цифровых массивов импортированы в модель наблюдателя (см. рис. 2b). Расчетные временные зависимости, полученные при обработке массивов, представлены на рис. 6. Видно, что этот режим является аварийным с точки зрения динамических нагрузок на шпинделях (окна 2, 3). Амплитудные значения моментов, восстановленных с помощью наблюдателя М _ШВmax, М _ШНmax, на обоих шпинделях превышают установившийся момент прокатки ( М _СТ = 200 %) более чем в 3,7 раза и достигают 750 % номинального момента двигателя, равного 1,91 МН·м.

Главными проблемами, возникающими при предотвращении аварийных режимов, являются своевременная фиксация начала аварии и форми-

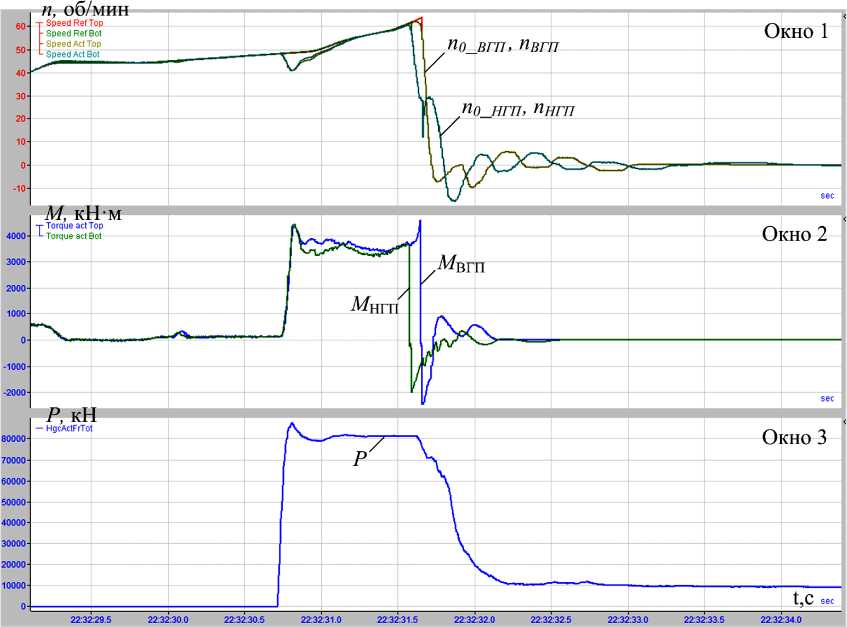
Рис. 5. Осциллограммы при аварийном отключении электроприводов во время прокатки: окно 1 – заданные и фактические скорости ВГП и НГП; окно 2 – моменты двигателей; окно 3 – усилие прокатки Fig. 5. Oscillograms in case of emergency shutdown of electric drives during rolling: window 1 – set and actual speeds of ВГП and НГП; window 2 – motor moments; window 3 – rolling force

рование сигнала на быстрый о станов электропр и водов. Также необходимо экстренное информир о вание оператора о подобных ситуациях, что обе с печит его своевременную реакцию на развитие аварии. В этом случае произойдет потеря заготов ки, однако это позволит избежать поломок механ ического обо рудования (также с потерей заготовки).

Обсуждение результатов и выводы

В настоящее время разработанный наблюд атель внедрен и находится в режиме опытно -про мышленной эксплуатации на стане 5000. По сра в нению с «контактными» измерительными сист е мами он обладает следующими преимуществами:

• •    простотой и высокой надежностью;

• •    отсутствием необходимости какого -либо обслуживания;

• •    практически не имеет стоимости, так как является фрагментом программного обеспечения.

Поскольку нагрузка электропривода (см. рис. 1) представлена в виде «черного ящика», он может быть применен как в одномассовой, так и в двух - и трехмассовых системах. Прин цип виртуальной н астройки регулятора в этих случаях не изменяется.

Полученные сигналы упругих моментов на шпинделях не предназначены для использования в системах регулирования электроприводов. Их основное назначение – информация об амплитудах упругого момента в динамических режимах. Также наблюдатель позволяет осуществлять контроль предаварийных ситуаций с целью предотвращения аварий, а в случае их возникновения – выполнять анализ причин и последствий.

Информацию о динамических моментах на шпинделе следует сохранять в специальной информационной базе, при этом амплитудные значения, многократно превышающие заданный порог, следует выводить в специальном окне на мониторе оператора. Это позволит избежать последовательного повторения динамических ударов, приводящих к усталостным разрушениям.

Для полноценной реализации возможностей наблюдателя целесообразно разработать и внедрить на стане:

• 1)    систему мониторинга перегрузок шпинделей, обеспечивающую фиксацию и подсчет перегрузок по моменту, превышающих заданные пороговые значения;

• 2)    методику расчета ресурса шпинделей по результатам подсчета перегрузок и оценки их амплитуд;

• 3)    способы ограничения динамических нагрузок.

Необходимо представить методику расчета параметров регулятора автонастройки. Это позволит рассчитывать и внедрять наблюдатель на дру- гих прокатных станах. Также следует решить вопрос с восстановлением скорости неуправляемой массы – валка.

Решение перечисленных задач позволит трансформировать разработанный наблюдатель в систему онлайн-мониторинга технического состояния шпинделей. На ее основе будет внедрен комплекс разработок, направленных на предупреждение аварий и минимизацию их последствий.