Наблюдатели состояния асинхронного электропривода на основе фильтра Калмана

Цитирование: Пахомов А. Н. Наблюдатели состояния асинхронного электропривода на основе фильтра Калмана / А. Н. Пахомов, А. А. Федоренко, К. С. Федий. Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(5). С. 575–583. EDN: EYPOUM

В настоящее время в промышленности отмечается повышенный интерес в использовании и развитии асинхронного электропривода. Повсеместное применение частотно-регулируемого электропривода обусловлено высокими показателями регулирования, возможностью автоматизации технологического процесса, повышением энергоэффективности производства.

С целью повышения динамических показателей и возможностью регулирования момента на валу асинхронного двигателя (АД) целесообразно использовать векторный способ управления переменными АД [1]. Для исключения из системы электропривода дорогостоящих датчиков координат (скорости, момента, потокосцепления и др.) используются наблюдатели (идентификаторы) состояния, что позволяет перейти к бездатчиковому векторному управлению асинхронным электроприводом [2].

В статье рассматривается применение фильтра Калмана в качестве наблюдателя состояния переменных АД. Для обеспечения универсальности электропривода и повышения его надежности ставится задача идентификации текущего значения угловой скорости ротора АД. Актуальность задачи обусловлена стремлением разработчиков асинхронного электропривода исключить датчик скорости вращения ротора АД с целью удешевления системы и повышения её отказоустойчивости. Особенностью бездатчиковых систем управления электроприводов – 576 – является повышенная чувствительность к параметрическим возмущениям [3]. Поэтому в задачи исследований входит проверка робастности бездатчиковых электроприводов с различными идентификаторами состояния при изменении параметров двигателя.

Для реализации наблюдателей используются математические модели АД, состоящие из системы нелинейных дифференциальных уравнений. Рассмотрим два варианта математических моделей АД, различие которых заключается в выборе переменных состояния. В работе используется математическая модель обобщенной электрической машины в неподвижной системе координат α, β [4]. Для упрощения записи математических моделей АД и наблюдателей применяется аппарат пространства состояний.

В первом случае используется вектор состояния X и вектор управляющих воздействий U:

X = [iSa iSв VRа VRв ю]Т и U = [uSа uSв]Т, где isа, isв, usа, usв - компоненты пространственных векторов тока и напряжения статора АД; VRа, VRв — компоненты пространственного вектора потокосцепления ротора; ю - скорость вращения вала АД.

Тогда уравнения состояния АД можно записать в виде:

— = AX + BU и Y = CX, dt где Y = [iSа iSв]Т - вектор выходных переменных; матрицы динамики A, входа B и выхода C равны:

	-аи 0     а12 аи 0		Ьг 0
	0 -ап -аи ап 0		0 Ьх	[1 0 0 0 0
А = <	«14      0     —^15  -«16   0	S В = <	0 0	; с = [01000
	0     «14    «16   "«15   0		0 0
	0     0     0     0   0		0 0

Следует отметить, что для упрощения матриц принято допущение постоянства (стабилизации) скорости АД, т.е. d ю / dt = 0.

Коэффициенты матриц A , B, C можно определить согласно выражениям [5]:

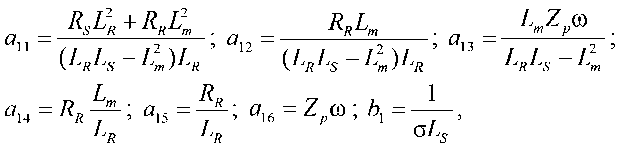
где L_S, L R , L m - индуктивности статора, ротора и контура намагничивания АД; R S , R R - активные сопротивления статора и ротора АД; Z_p – число пар полюсов АД.

Второй вариант математической модели АД отличается составом переменных состояния:

X = [iSa is в iR а iR в ю]Т, где iRа, iRв - компоненты пространственного вектора тока ротора АД.

В результате меняются матрицы A и B :

А = -

П25     ^26    ^27    ^28   ^ ^26    ^25    ^28   — ^27   ^ 0     0     0     0   0

> и В = <

' ^21      0 0     621 -622    0 0 -Ь2г .° 0 >

=

Коэффициенты матриц A, B можно определить согласно выражениям [6]:

Rs Vs         VsZp® LmRR LmLRZpto а = —— Ч---— ---* а ------— ' а =----—-— * а =-----—

• ²¹    L L L -£²) ’ ²² L L ’ ²³ L L ’ ²⁴ L L -L²

LmRs        LsRmZp®        R$Rr        Rs^rZp® л =---——-— * a —-----—— * л =----——— * a =—— *

• ²⁵    LL -L² ’ ²⁶ LL -L² ’ ²⁷ L L -L² ’ ²⁸ L L -L² ’

• b =—- +----■ ь =

• ²¹ L   L (L L -L²}   ²² L L -L² "

^LS ^sV^R^S ^m)        ‘-rJ-S ^m

Уравнения наблюдателя состояния системы, выполняемого, как правило, на базе микропроцессорных устройств, включают в себя вектор измерений Y k на k -ом шаге расчета (вектор из компонентов тока статора i S α и i S β ) и имеют следующий вид:

Хк=Ак.Хк_^В-ик_х;

Xk=Xk+Kk.(Yk-C-Xk), где Хк - вектор оценки состояний системы; Kk - матричный коэффициент, определяемый фильтром Калмана на основе выполненных измерений.

Оптимальное значение коэффициентов матрицы усиления Калмана K k зависит от характера шумов и случайных возмущений и обновляется на каждом шаге с помощью специального алгоритма, который реализован в соответствии с идеей адаптивной фильтрации:

где R - матрица ожидаемой дисперсии ошибки измерений, определяемой средней погрешностью измерений тока статора σ i (при нулевом среднем дисперсия ошибки равна матожиданию погрешности во второй степени):

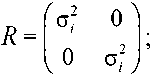
– предсказанная на k -ом шаге оценки   матрица ковариации ошибки:

Рк =А-Рк_х-АТ ^Q

В последнем выражении используется матрица ковариации случайных воздействий Q, значения которой определяются дисперсией соответствующих случайных переменных состояния системы, и скорректированная на ( k -1)-ом шаге матрица ошибки ковариации:

РкА=РкА-Кк_х -С.Рк_х

На каждом шаге рекуррентной процедуры обновляется матричный коэффициент K k таким образом, чтобы влияние шумов процесса и измерений на качество оценки вектора X_k минимизировалось [5–7].

На рис. 1 показана схема имитационного моделирования АД (блок AD ) с наблюдателем (блок IDENT ) в программной среде MATLAB Simulink . В качестве исследуемого АД был принят двигатель типа АИР 90L4 с номинальной мощностью Р _н = 2,2 кВт и синхронной частотой вращения n ₀ = 1500 об/мин.

Блоки AD и IDENT созданы с помощью S -функций, содержащих уравнения АД, и наблюдателя в виде программного кода встроенного языка программирования MATLAB . В качестве математического описания АД принята классическая модель в переменных i_S , ψ _R [8]. На вход блока AD подаются компоненты вектора напряжения статора u_{S α} и u_S β , созданные блоком Sourse [9], а также момент нагрузки M_c . Входными сигналами для наблюдателя являются статорные напряжения u S α , u S β и токи i S α , i S β эталонной модели АД.

На рис. 2 представлены графики переходных процессов угловой скорости ω _и с помощью рассмотренных вариантов фильтра Калмана при пуске вхолостую и последующем набросе номинальной нагрузки. В начале пуска видно отклонение графиков переходных процессов идентифицированной скорости от «эталонной», однако при приближении к установившемуся режиму и при набросе нагрузки фильтр Калмана достаточно точно позволяет оценить скорость АД.

Таким образом, оба варианта фильтра Калмана позволяют получить одинаковый результат идентификации скорости АД. Отклонение в динамических режимах можно объяснить отклонением стартовых значений матрицы ковариации, а также допущений, принятых при построении модели наблюдателя.

Рассмотрим работу наблюдателей при вариации параметров АД. На рис. 3 и 4 представлены графики переходных процессов оценки скорости вращения АД с помощью фильтра Калмана в переменных i S , i R при изменении на 10 % значений активных сопротивлений обмоток двигателя.

Нетрудно видеть, что при увеличении активного сопротивления статора (рис. 3б) и уменьшении сопротивления ротора (рис. 4а) фильтр Калмана в переменных i_S , i_R не справляется с задачей идентификации скорости АД.

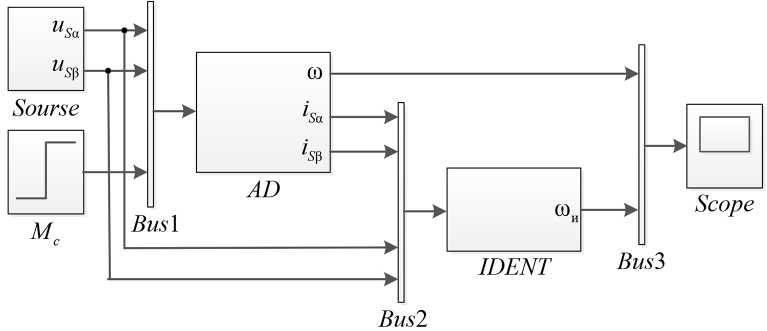
Рис. 1. Схема имитационной модели в среде MATLAB Simulink

Fig. 1. The scheme of the simulation model in the MATLAB Simulink environment

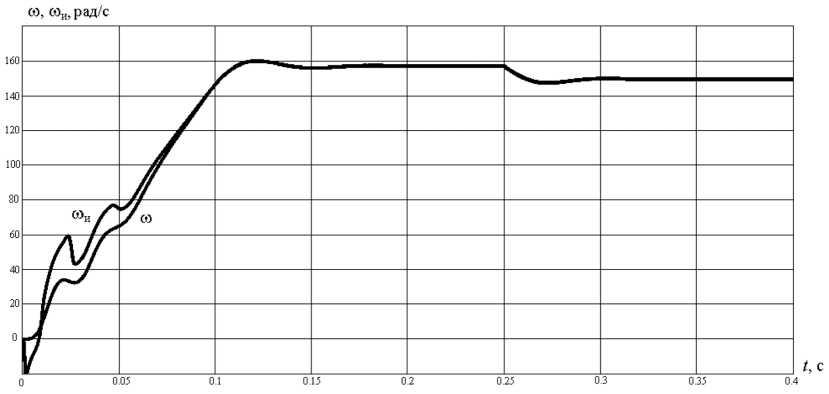
Рис. 2. Переходные процессы угловой скорости АД и её оценки фильтром Калмана

• Fig. 2.    Transients of the angular velocity of AD and its estimates by the Kalman filter

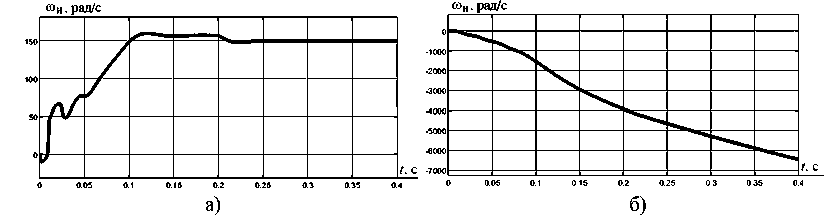
Рис. 3. Переходные процессы в электроприводе с фильтром Калмана в переменных i_S , i_R при снижении (а) и увеличении (б) активного сопротивления статора

• Fig. 3.    Transients in an electric drive with a Kalman filter in variables i_S , i_R , with a decrease (a) and an increase (б) in the active resistance of the stator

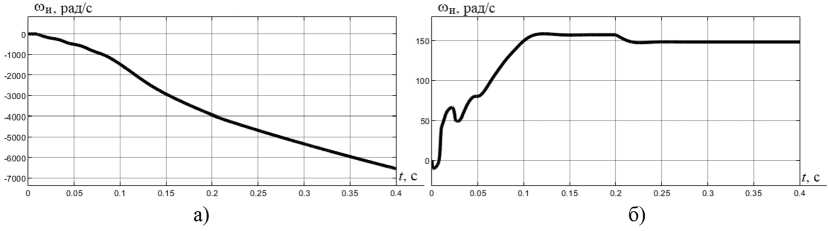
Рис. 4. Переходные процессы в электроприводе с фильтром Калмана в переменных i_S , i_R при снижении (а) и увеличении (б) активного сопротивления ротора

• Fig. 4.    Transients in an electric drive with a Kalman filter in variables i_S , i_R , with a decrease (a) and an increase (б) in the active resistance of the rotor

На рис. 5, 6 представлены переходные процессы идентифицированной угловой скорости вращения вала АД фильтром Калмана в переменных i S , ψ R при изменении на 10 % значений активных сопротивлений обмоток двигателя. Оценка фильтром переходных процессов угловой скорости выполняется во всех случаях.

На рис. 7 приведены переходные процессы оценки угловой скорости вращения вала двигателя рассмотренными вариантами фильтров Калмана при увеличении эквивалентного момента инерции в 5 раз. Причиной изменения указанного параметра может послужить подключение механизма к электроприводу, работавшему на холостом ходу. Фильтр Калмана в переменных i_S , i_R (рис. 7а) также не справляется с задачей идентификации скорости АД. Фильтр Калмана в переменных i S , ψ R выполняет поставленную задачу.

Проведенные исследования показали, что в качества идентификатора состояния АД, имеющего самую низкую чувствительность к вариации его параметров, является фильтр Калмана в переменных i_S , ψ _R , что позволяет рекомендовать его для использования в качестве наблюдателя состояния АД в бездатчиковых системах асинхронного электропривода с векторным управлением.

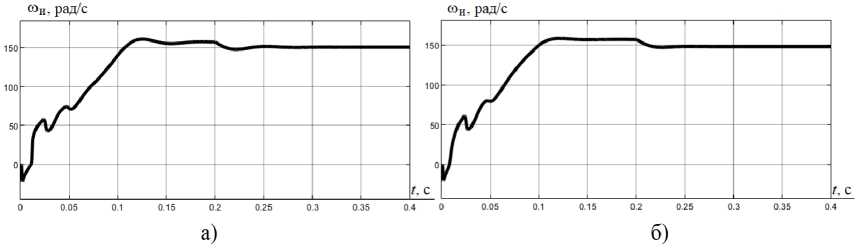
Рис. 5. Переходные процессы в электроприводе с фильтром Калмана в переменных i S , ψ R при снижении (а) и увеличении (б) активного сопротивления статора

Fig. 5. Transients in an electric drive with a Kalman filter in variables i_S , ψ _R , with a decrease (a) and an increase (б) in the active resistance of the stator

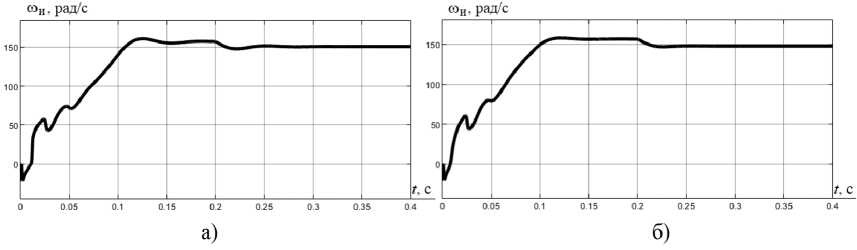
Рис. 6. Переходные процессы в электроприводе с фильтром Калмана в переменных i_S , ψ _R при снижении (а) и увеличении (б) активного сопротивления ротора

Fig. 6. Transients in an electric drive with a Kalman filter in variables i_S , ψ _R , with a decrease (a) and an increase (б) in the active resistance of the rotor

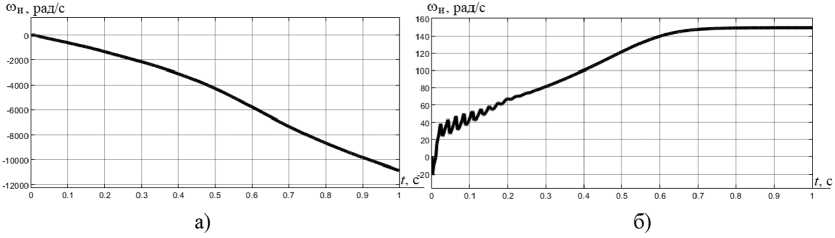
Рис. 7. Переходные процессы при увеличении момента инерции в бездатчиковом электроприводе с фильтром Калмана в переменных i_S , i_R (а) и i_S , ψ _R (б)

Fig. 7. Transients with an increase in the moment of inertia in a sensorless electric drive with a Kalman filter in variables i_S , i_R (a) and i_S , ψ _R (б)