Наблюдение оптического эффекта "углового трактора" в пучке Бесселя
Автор: Котляр Виктор Викторович, Ковалв Алексей Андреевич, Порфирьев Алексей Петрович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 4 т.42, 2018 года.
Бесплатный доступ
В работе изучается оптический эффект «углового трактора», заключающийся в том, что в вихревом лазерном пучке с радиальной симметрией с положительным/отрицательным топологическим зарядом и левой/правой круговой поляризацией на разных радиусах от центра пучка в поперечном сечении поток световой энергии вращается в разных направлениях (по часовой или против часовой стрелки). Показано, что этот эффект имеет место как для параксиальных вихревых пучков, так и в фокусе апланатической системы при фокусировке непараксиального оптического вихря. Экспериментально продемонстрировано движение диэлектрических микрочастиц в пучке Бесселя 3-го порядка с круговой поляризацией в разные стороны (по часовой и против часовой стрелки).
"угловой трактор", поток энергии, пучок бесселя
Короткий адрес: https://sciup.org/140238418
IDR: 140238418 | DOI: 10.18287/2412-6179-2018-42-4-550-556
Текст научной статьи Наблюдение оптического эффекта "углового трактора" в пучке Бесселя
В оптике с недавних пор (с 2010 года) известен эффект «оптического трактора» [1 –9]. Он заключается в таком взаимодействии светового поля с микрочастицей, которое приводит к тому, что сила, действующая со стороны поля на частицу, заставляет её двигаться против направления распространения освещающего её пучка. Такую силу называют негативной оптической силой [9]. Если говорить просто, то такая ситуация возникает, когда частица рассеивает больше света вперёд, чем отражает назад. И поэтому «по закону сохранения импульса» должна двигаться назад, если нет поперечных градиентных сил, удерживающих её. С другой стороны, известно такое явление, как обратный поток энергии. Ещё в 1959 году было показано [10], что при фокусировке плоской волны с линейной поляризацией с помощью апланатической системы в плоскости фокуса в области у основания основного лепестка интенсивности имеется область, в которой поток световой энергии направлен в обратную сторону по отношению к направлению распространения падающей плоской волны. В этой области продольная проекция вектора Пойнтинга имеет небольшое отрицательное значение, примерно 1% от максимального потока в прямом направлении. Аналогичный результат был получен ранее В.С. Игнатовским [11] ещё в 1920 году. Однако значения этому эффекту не придавали из-за его небольшой величины. В современных работах также рассматриваются разные аспекты аномального распространения светового потока [12–17]. Например, в [12] теоретически рассматривается угловой момент вихревого Гауссова пучка в области острого фокуса. Показано, что для мод Лагерра–Гаусса с топологическим зарядом больше 2 и круговой поляризацией вблизи оптической оси имеет место обратный поток световой энергии по отношению к направлению светового пучка. Обратный поток энергии по отношению к направлению распространения пучка надо отличать от эффекта «оптического трактора» [1]. В [1] рассмотрена суперпозиция двух произвольных световых полей, у которых разные проекции волнового вектора на продольную ось. Показано, что у таких световых полей имеют место локальные области, в которых продольная компонента силы, действующей на микрочастицу, направлена против волнового вектора светового пучка. В [13] численно показано наличие обратного потока на оптической оси в фокусе вихревой металинзы первого и второго порядков. В [14] численно показано наличие обратного распространения энергии в векторном пучке Бесселя с дробным топологическим зарядом. Такой световой пучок фактически является линейной комбинацией счётного числа обычных мод Бесселя. В [15] теоретически получены выражения для плотности вектора Пойнтинга для векторных Х-пучков и необходимые условия для появления обратного потока энергии. В [16] численно показано наличие обратного течения энергии в непараксиальном ускоряющемся 2D-пучке Эйри. В [17] теоретически с помощью локального волнового вектора рассматриваются условия, которые нужно наложить на световое поле, чтобы оно локально проявляло обратное распространение (или имел место обратный поток энергии). Это два разных явления, когда поток световой энергии локально направлен против общего потока энергии в пучке и когда сила света заставляет микрочастицу двигаться против освещающего её света и по направлению к источнику света. Хотя иногда одно из этих двух явлений становится причиной другого. Если эти эффекты «оптического трактора» и обратного потока энергии являются продольными эффектами и уже широко известны, то поперечный эффект «углового трактора» почти не известен. Он кратко отмечен в [12, 18] и подробно разбирается в [19]. Оптический эффект «углового трактора» [19] заключается в том, что в поперечной плоскости оптического вихря (параксиального [19] или непараксиального [18]) с радиальной симметрией и круговой поляризацией поперечный поток энергии вращается на разных расстояниях от оптической оси либо по часовой стрелке, либо против часовой.
В данной работе теоретически и экспериментально изучается эффект «углового трактора» в фокусе лазерного пучка Бесселя 3-го порядка с обратной (по отношению к направлению вращения спирали волнового фронта) круговой поляризацией. Впервые экспериментально продемонстрировано вращение в одном пучке нескольких диэлектрических микрочастиц по окружностям разного радиуса в разные стороны (по часовой стрелке и против неё).
вихря, в которых радиальная производная интенсивности отрицательная (∂ I / ∂ r <0). Для оптического вихря с линейной поляризацией (σ =0) плотность УМ (5) во всех точках поперечного сечения пучка положительная ( j z >0), если топологический заряд положительный ( n >0). Для круговой поляризации радиусы, на которых осевая проекция углового момента (5) меняет знак, и в которых j z =0, можно найти из уравнения:
, , 2 d| A ( r , z )|2
2 .A ( r , z ) =g r -1—---L . (6)
d r
1. Угловой трактор в параксиальном случае
В [13] получено общее выражение для плотности углового момента (УМ) произвольного параксиального оптического вихря с эллиптической поляризацией:
Например, для пучка Бесселя A ( r ) = J n ( k r r ), где J n ( x ) – функция Бесселя первого рода n -го порядка и k r – поперечная проекция волнового вектора, уравнение (6) принимает конкретный вид:
. - z j = T"
2 to
n ( 1 +IgI 2 )l A ( r , z )| 2 - Re G d A d r’z )
J j. ( k r r ) = r "Jn^k r r 1 g d r
.
r +
+ 1 +h 2
2 c
zF —| A ( r, z )|2 r
Ф +
+— 2 to
n ( 1 + |g| 2 )| A ( r , z )| - Re g r dr-
z .
В (1) ( r , ф , z ) - единичные вектора в цилиндрической системе координат.
Проекция на ось x вектора напряжённости электрического поля оптического вихря с радиальносимметричной интенсивностью имеет вид:
E x = A ( r , z ) exp ( in ф ) ,
функция F в (1) имеет вид:
f =- Г A * d A - A 1 .
k I d r d r J
Поперечные проекции Ex и Ey вектора напряжённости электрического поля E для волны с эллиптической поляризацией связаны соотношением
E = i g E . yx
Из (1) видно, что в случае круговой поляризации ( g =±1) проекция плотности УМ на оптическую ось может менять знак в зависимости от радиальной координаты r :
■ 1 Г d2 g r 51 A ( r , z )|2
J= = - nA(r,z) 1 to 2 dr
Если топологический заряд положительный ( n >0), то при правой поляризации (σ >0) проекция УМ (5) может быть отрицательной ( j z <0) в тех местах поперечного сечения оптического вихря, в которых радиальная производная интенсивности I =| A ( r , z )|2 положительная (∂ I / ∂ r >0), и наоборот, для левой поляризации (σ <0) проекция УМ (5) может быть отрицательной ( jz <0) в тех местах поперечного сечения оптического
Из (7) следует, что осевая проекция плотности УМ будет отрицательной j z <0 (при n / σ >0) при
J n ( k r r ) [ ( 1 - G ) J n - 1 ( k r r ) + ( 1 + G ) J n + 1 ( k r r ) ] < 0 , (8)
то есть J n ( k r r ) J n +1 ( k r r )<0 для правой круговой поляризации и J n ( k r r ) J n –1 ( k r r )<0 для левой круговой поляризации. Известно, что нули функций Бесселя соседних порядков чередуются (выражение 9.5.2 в [17]):
Y v ,1 < Y v + 1,1 < Y v ,2 < Y v + 1,2 < Y v ,3 < ... , (9) где γ ν , m – m -й ноль функции Бесселя ν -го порядка. Поэтому в случае правой круговой поляризации угловой трактор наблюдается при γ n , m < k r r < γ n +1, m ( m = 1, 2, ...), то есть на внутренних сторонах светлых колец (начиная со второго), а в случае левой круговой поляризации – при γ n –1, m < krr < γ n , m ( m = 1, 2, ...) , то есть на внешних сторонах светлых колец (начиная с первого).
2. Угловой трактор в фокусе непараксиального оптического вихря
В этом параграфе покажем, что в плоскости фокуса в апланатической системе также имеет место эффект углового трактора. Можно получить общие соотношения для поперечных составляющих вектора Пойнтинга [10] S = c Re[ E * H ]/(8 n ) в плоскости фокуса оптического вихря с топологическим зарядом m и левой круговой поляризацией σ =–1 (с точностью до с / (8π), c – скорость света в вакууме):
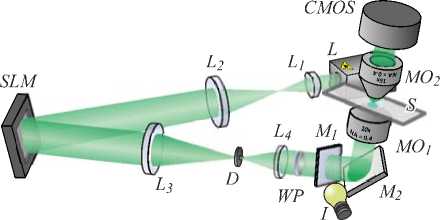
^ x - = - Q m ( r ) sin ф , S y - = Q m ( r ) cos ф , гДе Q m ( r ) = ( I 0, m + I 2, m - 2 ) ( 1 2, m - 1 + 1 >, m - 1 ) +
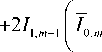
I + 2( m - 1) I )
1 2,m-2 + 7 J1,m-1 I, kr )
a
1 0 , m = B J sin 0 cos 1/2 0 A m ( 0 )(1 + cos 0 ) Jm ( x ) d 0 ,
a
1 1, m ± 1 = B J Sin 2 0 cos 1/2 0 A m ( 0 ) J m ti( x )d 0 , (12)
a
1 2, m ± 2 = B J sin 0 cos 1/2 0 A m ( 0 )(1 - COs 0 ) J m ± 2 ( X ) d 0 ,
10 , m = B J sin 0 cos 3/2 0 A m ( 0 )(1 + cos 0 ) J m ( x ) d 0 ,
a
I o, m _ , = B J sin 2 0 cos 1/2 0 A m ( 0 )(1 + cos 0 ) J m _ , ( x ) d 0 ,
a
1 2, m ± 2 = B J sin 0 cos 3/2 0 A m ( 0 )(1 - cos 0 ) J m ± 2 ( x ) d 0 ,
a
1 2,m ± 1 = B J sin 2 0 cos 1/2 0 A m ( 0 )(1 - cos 0 ) J m ± 1 ( x ) d 0 .
В (12) использованы обозначения: B = kf / 2, a = arcsin( NA ), x = kr sinO, y ± = (1 ± o ) ' 2, Jv (x) — функция Бесселя, k – волновое число света, f – фокусное расстояние апланатической системы с числовой апертурой NA . Из (10) видно, что в плоскости фокуса поток энергии вращается вокруг оптической оси по часовой или против часовой стрелки, в зависимости от знака функции Q m ( r ). Вблизи плоскости фокуса поток энергии будет вращаться по спирали. Чтобы далее получать аналитические выражения, ограничимся простым способом формирования в фокусе апланати-ческой системы непараксиального пучка Бесселя m -го порядка с левой круговой поляризацией с помощью функции аподизации в виде δ-функции:
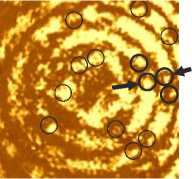
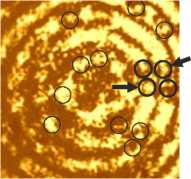
Am (0) = §(0-0o), 0 <00 Подставив (13) в (12), вместо интегралов получим: I0,m = B sin 0o cos1/2 0o(1 + cos 0o) Jm(x0), 11,m-1 = B sin2 00 cos1'2 00 Jm-1(x0), I2,m-2 = B sin 00 cos1'200 (1 - cos 00 ) Jm-2 (X0 ), 10,m = B sin 00 cos3'2 00 (1 +cos 00 ) Jm(x0 ), 10,m-1 = B sin2 00 cos1'2 00 (1 +cos 00 ) Jm-1 (x0 ), 1>,m-2 = B sin 00 cos3'2 00 (1 -cos 00 ) Jm-2 (X0 ), 12,m-1 = B sin2 00 cos1'2 00 (1 -cos 00 ) Jm-1 (x0 ), где x0 = kr sin 00. Тогда с учётом (14) вместо (11) запишем: Qm(r) = Jm-1( x 0)x X[ A0 Jm(x0 ) + B0 Jm-1 (x 0 ) + C0 Jm - 2 (x 0 )], где Ay = 2B2sin300 cos 00 (1 + cos 00 )2, 4(m -1)BB B„ = sin 0„ cos 0,,,(16) 0k00 C0= 2B2sin300 cos 00 (1 - cos 00 )2. Используя рекуррентные соотношения для функ ции Бесселя, получим из (15): Qm (r) = 4 B2 sin3 00 cos 00 Jm-1 ( x0 )X x[(1 + cos 00 ) Jm (x0 ) +(1 - cos 00 ) Jm-2 (x0 )] - Определим, на каких радиусах в распределении интенсивности пучка Бесселя в фокусе происходит эта смена вращения потока энергии. Можно показать, что интенсивность в плоскости фокуса оптического вихря (2) с левой круговой поляризацией равна: Im (r, Z = 0) = 2 (102,m + 122,m-2 + 212m-1 ) -(18) С учётом (12) и (14) для пучка Бесселя m-го порядка получим: im (r)=d0 Jm( x0)+e0 Jm-1( x 0)+fJm-2( x 0),(19) где положительные константы равны: D0= 2B2sin200 cos 00(1 + cos 00)2, E0 = 4B2 sin4 00 cos 00,(20) F0= 2B2sin200 cos 00(1 - cos 00)2. Для небольших числовых апертур (NA< 0,5) D0 >> E0 и D0 >> F0. Поэтому минимумы интенсивности (тёмные кольца) достигаются примерно на радиусах rn2 = уm,n'(ksin00), n =1, 2, -... Это означает, что отрицательные значения углового потока энергии Qm(r) наблюдаются на внешних сторонах колец интенсивности. На рис. 1 показана зависимость интенсивности Im(r) и функции Qm(r) от радиальной координаты r для длины волны X = 532 нм, топологического заряда m =3 и числовой апертуры NA = 0,4. Вертикальными пунктирными линиями отмечены значения rn1 и rn2. Рис. 1. Зависимость интенсивности Im(r) и функции азимутального потока энергии Qm(r) от радиальной координаты r для длины волны А = 532 нм, топологического заряда m = 3 и числовой апертуры NA = 0,4. Вертикальные пунктирные линии показывают радиусы rn1 и rn2 Из рис. 1 видно, что, действительно, на внутренних сторонах и центрах светлых колец поток энергии вращается против часовой стрелки (Qm(r) > 0), а на внешних сторонах светлых колец – по часовой стрелке (Qm(r) < 0), то есть почти так же, как и в параксиальном пучке Бесселя (7) – (9). Таким образом, если в плоскости фокуса непараксиального пучка Бесселя 3-го порядка (m = 3) с левой круговой поляризацией поместить две диэлектрические микрочастицы, сравнимые по размеру с шириной светлых колец картины дифракции пучка Бесселя, то частица, захваченная на внешней стороне второго светлого кольца, должна вращаться по часовой стрелке, а частица, захваченная на внутренней стороне третьего светлого кольца, должна вращаться против часовой стрелки. Эксперимент подтверждает такое вращение микрочастиц. 3. Эксперимент по вращению микросфер полистирола в пучке Бесселя с круговой поляризацией На рис. 2 показана оптическая схема установки, использованной в эксперименте. Линейно-поляризованный лазерный пучок с Гауссовым профилем распределения интенсивности расширялся с помощью системы линз L1 и L2 ( f1 =150 мм, f2=350 мм) и направлялся на дисплей пространственного модулятора света SLM (HOLOEYE, PLUTO-VIS). Модулятор света был использован для реализации фазовой маски элемента, формирующего пучок Бесселя 3-го порядка, в виде τ(r, ϕ) =circ(r / R) sgn Jn(αr) exp(inϕ), где (r, ϕ) – полярные координаты, параметр α задаёт масштаб функции Бесселя n-го порядка Jn (x), R – радиус элемента. Дополнительно к полученной фазовой маске добавлялась градиентная фазовая маска для того, чтобы развести в пространстве непромодулированный нулевой дифракционный порядок и 1-й дифракционный порядок, в котором формировался требуемый пучок Бесселя. Для преобразования сформированного линейно-поляризованного пучка Бесселя в пучок Бесселя с круговой поляризацией была использована четвертьволновая пластинка WP. Отражённый от модулятора и промодулированный по фазе лазерный пучок с помощью системы линзы L3, L 4 (f3=350 мм, f4= 150 мм) и зеркала M 2 направлялся во входное отверстие микрообъектива MO1 (20×, NA =0,4), который выполнял фокусировку лазерного пучка в раствор с 5 микрометровыми полистироловыми сферами на подложке S. При этом диафрагма D блокировала нулевой (нерабочий) дифракционный порядок. Микрообъектив MO2 (16×, NA =0,3) строил изображение плоскости манипулирования на матрице CMOS-видеокамеры. Для подсветки плоскости манипулирования был использован свет светодиодной лампочки I, для ввода которого было использовано полупрозрачное зеркало M1. Для ослабления лазерного пучка после второго микрообъектива были использованы фильтры нейтральной плотности (не показаны на схеме). Рис. 2. Экспериментальная схема: L – твердотельный лазер (λ = 532 нм), L1 , L2 , L3 , L 4 – линзы с фокусными расстояниями (f1 = 150 мм, f2 = 350 мм, f3 = 350 мм, f4 = 150 мм), SLM – пространственный модулятор света (HOLOEYE, PLUTO-VIS), D – диафрагма, WP – четвертьволновая пластинка, M1 и M2 – зеркала, MO1 микрообъектив (20×, NA = 0,4), MO2 (16×, NA = 0,3), S – подложка с раствором с 5-микрометровыми полистироловыми сферами, I – светодиодная лампочка, CMOS – видеокамера На рис. 3 показано распределение интенсивности сформированного пучка Бесселя 3-го порядка с левой круговой поляризацией и стадии движения пар частиц по второму и третьему кольцу. Очевидно, что частицы, захваченные по внешнему краю второго светового кольца, движутся по часовой стрелке, а частицы, захваченные по внутреннему краю третьего светового кольца, движутся против часовой стрелки – навстречу двум частицам во втором кольце. Измеренная скорость движения частиц по второму кольцу составила 0,9±0,1 мкм / с, по третьему кольцу – 0,7±0,1 мкм / с. Мощность лазерного пучка в плоскости захвата – около 80 мВт. Рис. 3. Вращение 5 микрометровых сфер полистирола в пучке Бесселя 3-го порядка с левой круговой поляризацией: распределение лазерного пучка в плоскости захвата микросфер (а), стадии движения захваченных частиц (интервал между кадрами 5 с) (б). Размер кадров 60×60 мкм. Кружками отмечены положения всех микросфер, а стрелочки указывают положения микросфер, перемещающихся в противоположных направлениях Заключение В работе получены следующие результаты. Изучен оптический эффект «углового трактора». Он состоит в том, что у оптического вихря с круговой поляризацией на разном расстоянии от оптической оси энергия будет распространяться либо по правой, либо по левой спирали. Для параксиального вихревого светового поля с круговой поляризацией показано, что проекция на оптическую ось вектора плотности углового момента на некоторых расстояниях от оптиче- ской оси меняет знак, то есть имеет место «угловой трактор». Для непараксиального вихревого светового поля с любым целым топологическим зарядом m и круговой поляризацией получены общие выражения для интенсивности и поперечных проекций вектора Пойнтинга в плоскости фокуса в апланатической системе. Из общих формул в простом частном случае для узкой функции аподизации падающего вихревого поля c небольшой числовой апертурой NA <0,5 показано, что поперечный поток энергии в плоскости фокуса вращается вокруг оптической оси и меняет направление вращения вблизи радиусов тёмных колец, которые пропорциональны корням (нулям) функции Бесселя второго порядка. Эффект «углового трактора» экспериментально наблюдался с помощью захвата и вращения в разные стороны полистироловых шариков диаметром 5 мкм в плоскости фокуса лазерного пучка Бесселя 3-го порядка с круговой поляризацией. Причём частицы, захваченные на внешней стороне второго светлого кольца, вращались по часовой стрелке, а захваченные на внутренней стороне третьего светлого кольца – против часовой стрелки. Работа выполнена при поддержке Министерства науки и высшего образования РФ (соглашение № 007-ГЗ/Ч3363/26) в части «Угловой трактор в параксиальном случае» и Российского научного фонда (грант 18-19-00595) в части «Угловой трактор в фокусе непараксиального оптического вихря».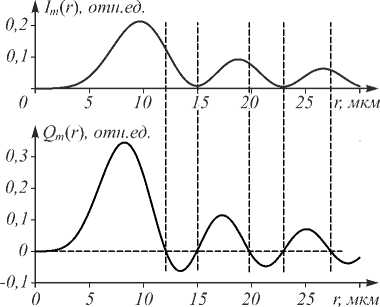


Список литературы Наблюдение оптического эффекта "углового трактора" в пучке Бесселя
- Sukhov, S. On the concept of "tractor beams"/S. Sukhov, A. Dogariu//Optics Letters. -2010. -Vol. 35, Issue 22. -P. 3847-3849. - DOI: 10.1364/OL.35.003847
- Novitsky, A. Single gradientless light beam drags particles as tractor beams/A. Novitsky, C. Qiu, H. Wang//Physical Review Letters. -2011. -Vol. 107, Issue 20. -203601. - DOI: 10.1103/PhysRevLett.107.203601
- Sukhov, S. Negative nonconservative forces: optical "tractor beams" for arbitrary objects/S. Sukhov, A. Dogariu//Physical Review Letters. -2011. -Vol. 107, Issue 20. -203602. - DOI: 10.1103/PhysRevLett.107.203602
- Sáenz, J.J. Laser tractor beams/J.J. Sáenz//Nature Photonics. -2011. -Vol. 5. -514-515. - DOI: 10.1038/nphoton.2011.201
- Dogariu, A. Optically induced "negative forces"/A. Dogariu, S. Sukhov, J.J. Saenz//Nature Photonics. -2013. -Vol. 7. -P. 24-27. - DOI: 10.1038/nphoton.2012.315
- Kajorndejnukul, V. Linear momentum increase and negative optical forces at dielectric interface/V. Kajorndejnukul, W. Ding, S. Sukhov, C.-W. Qiu, A. Dogariu//Nature Photonics. -2013. -Vol. 7. -P. 787-790. - DOI: 10.1038/nphoton.2013.192
- Shvedov, V. A long-range polarization-controlled optical tractor beam/V. Shvedov, A.R. Davoyan, C. Hnatovsky, N. Engheta, W. Krolikowski//Nature Photonics. -2014. -Vol. 8. -P. 846-850. - DOI: 10.1038/nphoton.2014.242
- Carretero, L. Periodic trajectories obtained with an active tractor beam using azimuthal polarization: design of particle exchanger/L. Carretero, P. Acebal, C. Garcia, S. Blaya//IEEE Photonics Journal. -2015. -Vol. 7, Issue 1. -3400112. - DOI: 10.1109/JPHOT.2015.2402123
- Mitri, F.G. Optical Bessel tractor beam on active dielectric Rayleigh prolate and oblate spheroids/F.G. Mitri//Journal of the Optical Society of America B. -2017. -Vol. 34, Issue 5. -P. 899-908. - DOI: 10.1364/JOSAB.34.000899
- Richards, B. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system/B. Richards, E. Wolf//Proceedings of the Royal Society A. -1959. -Vol. 253, Issue 1274. -P. 358-379. - DOI: 10.1098/rspa.1959.0200
- Ignatovsky, V.S. Diffraction by a lens having arbitrary opening/V.S. Ignatovsky//Transactions of the Optical Institute of Petrograd. -1919. -Vol. 1. -IV.
- Monteiro, P.B. Angular momentum of focused beams: beyond the paraxial approximation/P.B. Monteiro, P.A.M. Neto, H.M. Nessenzveig//Physical Review A. -2009. -Vol. 79, Issue 3. -033830. - DOI: 10.1103/PhysRevA.79.033830
- Котляр, В.В. Формирование и фокусировка векторного оптического вихря с помощью металинзы/В.В. Котляр, А.Г. Налимов//Компьютерная оптика. -2017. -Т. 41, № 5. -С. 645-653. - DOI: 10.18287/2412-6179-2017-41-5-645-654
- Mitri, F.G. Reverse propagation and negative angular momentum density flux of an optical nondiffracting nonparaxial fractional Bessel vortex beam of progressive waves/F.G. Mitri//Journal of the Optical Society of America A. -2016. -Vol. 33, Issue 9. -P. 1661-1667. - DOI: 10.1364/JOSAA.33.001661
- Salem, M.A. Energy flow characteristics of vector X-waves/M.A. Salem, H. Bagci//Optics Express. -2011. -Vol. 19, Issue 9. -P. 8526-8532. - DOI: 10.1364/OE.19.008526
- Vaveliuk, P. Negative propagation effect in nonparaxial Airy beams/P. Vaveliuk, O. Martinez-Matos//Optics Express. -2012. -Vol. 20, Issue 24. -P. 26913-26921. - DOI: 10.1364/OE.20.026913
- Berry, M.V. Quantum backflow, negative kinetic energy, and optical retro-propagation/M.V. Berry//Journal of Physics A: Mathematical and Theoretical. -2010. -Vol. 43, Issue 41. -415302. - DOI: 10.1088/1751-8113/43/41/415302
- Kotlyar, V.V. Circularly polarized Hankel vortices/V.V. Kotlyar, A.A. Kovalev//Optics Express. -2017. -Vol. 25, Issue 7. -P. 7778-7790. - DOI: 10.1364/OE.25.007778
- Котляр, В.В. Плотность углового момента параксиального оптического вихря с круговой поляризацией/В.В. Котляр, А.А. Ковалёв//Компьютерная оптика. -2018. -Т. 42, № 1. -С. 5-12. - DOI: 10.18287/2412-6179-2018-42-1-5-12


