Наблюдения дрейфово-компрессионных волн с помощью среднеширотного декаметрового когерентного радара

Одним из важных способов исследования околоземного космического пространства является изучение ультранизкочастотных (УНЧ) волн. Как показа- ли теоретические и экспериментальные исследования, УНЧ-волны могут быть разделены на две группы в соответствии с величиной их азимутального волнового числа m [Агапитов, Черемных, 2011].

УНЧ-волны с малыми значениями m имеют вне-магнитосферное происхождение [Козлов и др., 2015]. Быстрые магнитоакустические волны, формирующиеся на магнитопаузе или в солнечном ветре, распространяются внутрь магнитосферы и генерируют альфвеновские моды на тех L -оболочках, где частота волны совпадает с собственной частотой альфвеновских колебаний [Дмитриенко, 2010]. Изначальная быстрая мода может проникнуть в магнитосферу из солнечного ветра [Мазур, 2010; Потапов и др., 2012] или образоваться из-за взаимодействия неоднородностей солнечного ветра с магнитосферой [Золотухина, 2009; Мишин и др., 2013] или в результате МГД-неустойчивости на магнитопаузе [Гульельми и др., 2010; Мазур, Чуйко, 2013].

Эти механизмы генерации неэффективны для волн с большими значениями m , поскольку в этом случае в магнитосферу проникает малая доля энергии колебаний [Гульельми, Потапов, 1984]. Пульсации этого типа отождествляются с полоидальными альфвеновскими модами, генерируемыми благодаря внутренним процессам в магнитосфере, таким как различные плазменные неустойчивости [Southwood, 1980; Baddeley et al., 2005] или переменные токи, создаваемые дрейфующими частицами, инжектированными в магнитосферу во время суббури [Гулье-льми, Золотухина, 1980; Магер, Климушкин, 2007].

Тем не менее среди волн с большими значениями m можно выделить группу волн с частотами несколько ниже частот альфвеновских волн на соответствующих магнитных оболочках (буревые компрессионные волны Pc5). Волны этой группы были открыты благодаря спутниковым данным [Barfield, McPherron, 1972], а позднее обнаружены и по данным радаров [Allan et al., 1982; Walker et al., 1982].

Природа этих волн пока не ясна. С точки зрения теории МГД кажется очевидным отождествление их с наиболее длиннопериодической МГД-модой — медленным магнитным звуком (ММЗ) [Leonovich, Kozlov, 2013]. Однако не вполне понятно, может ли МГД-подход вообще использоваться для описания компрессионных УНЧ-мод в бесстолкновительной плазме [Hurricane et al., 1994]. Иногда буревые компрессионные Pc5-волны отождествляют с дрейфово-зеркальными модами [Kremser et al., 1981], но не ясно, достаточно ли высока температурная анизотропия магнитосферной плазмы для создания условий для зеркальной неустойчивости. Сомнения в соотнесении буревых компрессионных Pc5-пульсаций с дрейфово-зеркальной модой возникли с самого начала радарных наблюдений УНЧ-волн с m >>1 [Allan, Poulter, 1986].

Вероятно, наиболее подходящим объяснением буревых компрессионных пульсаций является дрейфово-компрессионная мода. Это наиболее типичная компрессионная УНЧ-мода в кинетике. Для ее существования требуются только конечное давление плазмы и неоднородность плазмы поперек магнитных оболочек. Эта мода может быть возбуждена благодаря наличию градиента концентрации горячей плазмы [Crabtree, Chen, 2004; Klimushkin, Mager, 2011], инверсного распределения горячих протонов

[Mager et al., 2013] или сцепления с альфвеновской модой из-за кривизны силовых линий [Klimushkin et al., 2012]. Частота этой моды имеет тот же порядок величины, что и диамагнитная частота, хотя и не совпадает с ней [Klimushkin, Mager, 2011; Mager et al., 2013; Naim et al., 2014]. Характерной особенностью дрейфово-компрессионной моды является зависимость ее частоты от волнового числа m .

Цель представленной работы — найти экспериментальные подтверждения того, что дрейфово-компрессионная мода может являться источником буревых компрессионных Pc5-пульсаций.

ОБОРУДОВАНИЕ

Pc5-пульсации наблюдались среднеширотным когерентным декаметровым радаром, расположенным около Екатеринбурга. Этот радар является аналогом радаров, используемых в международной сети SuperDARN (Super Dual Auroral Radar Network) [Greenwald et al., 1995; Chisham et al., 2007]. Радаром регистрируется радиосигнал, рассеянный как на неровностях земной поверхности, так и на мелкомасштабных неоднородностях F-слоя ионосферы, вытянутых вдоль магнитного поля [Ruohoniemi et al., 1987]. Угол обзора радара, составляющий 50°, разделен на 16 секторов, или лучей (рис. 1). Направление самого западного луча примерно совпадает с направлением на магнитный полюс. Радар регистрирует сигналы обратного рассеяния с расстояний 200–3000 км. Его поле обзора разделено на 75 диапазонов дальности, каждый из которых охватывает 45 км в радиальном направлении. Рабочая частота радара примерно 10.5 МГц.

Режим работы радара, использовавшийся при проведении эксперимента [Mager et al., 2015], предусматривает запись данных одновременно в двух каналах: канал 1 обеспечивает получение данных с 96-секундным разрешением для всех 16 лучей; на канале 2 производится дополнительное сканирование попеременно лучей 0–2 в течение 6 с, что дает 18-секундное разрешение для этих трех лучей. В этой работе мы анализируем только сигналы, рассеянные в ночные часы (18–24 UT) на расстоянии не

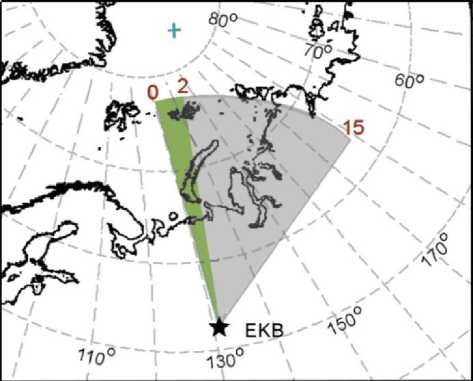
Рис. 1. Поле обзора екатеринбургского радара (ЕКВ). Номерами указано расположение лучей более 1500 км, поскольку для данного среднеширотного радара на малых расстояниях в ночной ионосфере условия для получения сигнала, рассеянного земной поверхностью, отсутствуют. Исходя из этого, мы полагаем, что все наблюдаемые сигналы являются сигналами обратного рассеяния на неоднородностях ионосферы. Таким образом, колебания доплеровского смещения частоты соответствуют изменениям скорости мелкомасштабных ионосферных неоднородностей вдоль направления луча. Считается, что эти изменения возникают благодаря электрическому дрейфу мелкомасштабных неоднородностей в магнитном поле Земли, вызванному магнитосферными УНЧ-волнами [Wright, Yeoman, 1999; Yeoman et al., 2012; Bland et al., 2014]. Поскольку направление луча 0 почти совпадает с магнитным меридианом, а лучи 1 и 2 близки к его направлению, измеренные скорости отражают меридиональную компоненту скоростей частиц. Эта компонента связана с азимутальной компонентой электрического поля, которая, в свою очередь, соответствует радиальной компоненте возмущения магнитного поля.

АНАЛИЗ ДАННЫХ

Двадцать шестого декабря 2014 г. в ночной ионосфере радаром были зарегистрированы колебания скорости ионосферной плазмы с амплитудой более 200 м/с. Такие скорости соответствуют колебаниям электрического поля с амплитудами выше 10 мВ/м. На рис. 2 показаны мощность принимаемого сигнала и вариации скорости, наблюдаемые на луче 0. Положительные и отрицательные значения скорости обозначают направление к радару и от него соответственно. Периодические вариации скорости плазмы начались примерно в 21:30 UT, а пик амплитуды колебаний пришелся на 23:00–23:30 UT, что приблизительно соответствует 02:30–03:00 MLT. Максимальные амплитуды колебаний наблюдались на расстоянии 630–900 км от радара (геомагнитные широты 58.5–60.5°). Вдоль луча 0 эта область соответствует магнитным оболочкам 4.7–5.4 (магнитные оболочки рассчитаны по модели IGRF, магнитные координаты — по модели AACGM). На рис. 3 показаны колебания, отфильтрованные в диапазоне пульсаций Pc5 и зарегистрированные в шести различных диапазонах в пределах этой области вдоль луча 0. Видно, что с ростом расстояния от радара фаза волны не меняется. Следовательно, фазовый фронт параллелен направлению луча, т. е. волна распространялась в азимутальном направлении и ее частота не зависела от номера магнитной оболочки. Из рассмотренных данных наиболее полными являются те, которые были получены на геомагнитных широтах 58.5–59.7° вдоль лучей 0 и 1, поэтому именно эти данные используются при дальнейшем анализе. Кроме того, из трех лучей, для которых использовался режим высокого временного разрешения, больше отклонен от направления на магнитный полюс луч 2, поэтому данные, полученные с его помощью, далее исключены из рассмотрения.

Для заполнения недостающих значений была проведена интерполяция данных, после чего использовался фильтр верхних частот с частотой от-

сечки 1.7 мГц. К полученным временным рядам данных примененялось вейвлет-преобразование Морле [Grossman, Morlet, 1984; Foster, 1996]:

W(to, т) = Vto^x(t7)eito^ tj) (т tj) 2TT ,           (1)

j = 1

где ω — циклическая частота, τ — смещение по времени, x ( t j ) — значения сигнала в N дискретных значений времени, где j =1, 2, …, N , T =2π/ω — период. Для вычисления спектра колебаний использовалась функция

F(to, т) =

2 W

tonn ( to, т )

где

N

n

(to, т)=!

e

j = 1

( т-9)7 2 ^{t 2}

Функция F (ω,τ) описывает вклад колебательных компонент в общий сигнал. В случае чистой синусоиды значение функции максимально и равно амплитуде колебаний на заданной частоте [Foster, 1996]. Вейвлет-преобразование Морле является комплексным и поэтому позволяет вычислять разность фаз двух сигналов, полученных на соседних лучах:

А ф = arctg

Im(W (to, т) W2* (to, т))

Re(W (to, т) W2* (to, т))

где W ( to, т ) и W ₂* ( to, т) — вейвлет-преобразование

для первого сигнала и комплексно-сопряженное преобразование для второго. Зная разность магнитных долгот Δλ двух лучей на заданной магнитной оболочке, мы можем вычислить азимутальное волновое число:

m = -

А ф

"

Следует заметить, что при определении координат точки рассеяния радиосигнала возможна ошибка в направлении луча до 200 км. Она приводит к ошибке в пределах 10 км в определении расстояния между точками рассеяния на соседних лучах. Разность магнитных долгот между лучами на тех широтах, на которых наблюдалось событие, меняется от 0.64 до 1.08° в зависимости от удаленности от радара. Систематическая ошибка определения волнового числа m при таких параметрах может достигать 25 %. Для вычисления разности фаз сигналов, полученных на лучах 1 и 2, использовалось кросс-вейвлет-преобразование:

^W 01 (^to , ^т) = ^W 0 (^to , ^т) W *(^to ’ ^т) , ⁽⁶⁾

где W_o и W ₁ * — вейвлет-преобразование и комплексно-сопряженное вейвлет-преобразование для сигналов на лучах 0 и 1 соответственно. Фаза кросс-вейвлет-преобразования является разностью фаз сигналов на лучах. Параметры преобразования вычислялись для тех точек на плоскости время — частота, где высока взаимная мощность

F 01 (ω, τ)= F 0 (ω, τ) F 1 (ω, τ); (7) здесь F ₀ и F ₁ — амплитудные функции сигналов.

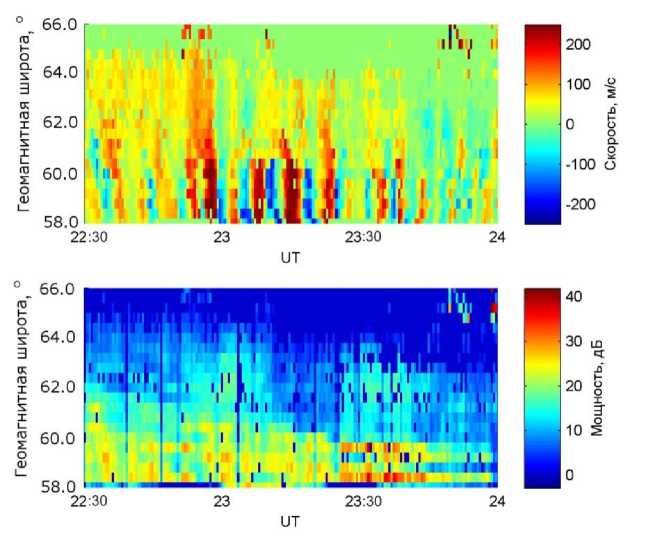
Рис. 2. Скорости плазмы вдоль луча 0 (вверху) и мощность сигнала на том же луче (внизу) 26 декабря 2014 г.

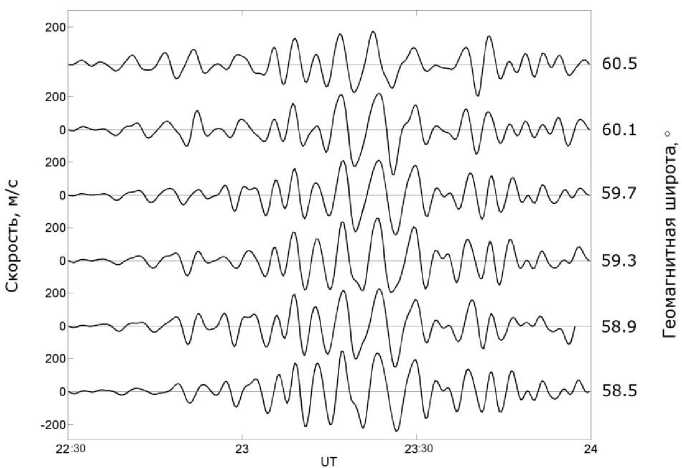
Рис. 3. Колебания скорости плазмы вдоль луча 0 на разных геомагнитных широтах

Сходный вейвлет-анализ данных екатеринбургского радара был проведен в работе [Mager et al., 2015].

В качестве примера на верхней панели рис. 4 показаны фильтрованные данные, полученные на лучах 0, 1 и 2 на геомагнитной широте 59.3°. По сдвигу фаз сигналов видно, что волна распространялась на запад. На нижней панели приведен пример кросс-вейвлет-спектра для рядов данных, полученных на лучах 0 и 1 для того же диапазона дальностей. Видно, что частота колебаний снизилась с 4.3 до 2.9 мГц за 0.3 ч, а затем выросла до 3.1 мГц в течение следующей 0.1 ч. Кросс-вейвлет-спектры рядов для других рассмотренных диапазонов расстояний на лучах 0–2 показывают схожие частотно-временные зависимости.

На верхних панелях рис. 5 представлены значения частоты и азимутального волнового числа m в максимумах кросс-вейвлет-спектров, построенных по данным, относящимся к четырем диапазонам дальности в интервале геомагнитных широт 58.5– 59.7°. Соответствующие медианные значения для этих параметров показаны на нижних панелях рисунка. Значения волнового числа m отрицательные, поскольку, как упоминалось выше, волна распространялась на запад; медианное значение его абсолютной величины уменьшается с 67 до 29. Фазовая скорость, вычисленная как V _ph = ω/ m , меняется в пределах от –6.3·10^–4 до –4.3·10^–4 рад/с. На рис. 4 и 5 видно, что монотонное снижение частоты прекратилось в 23:25 UT. Примерно в это же время перестала

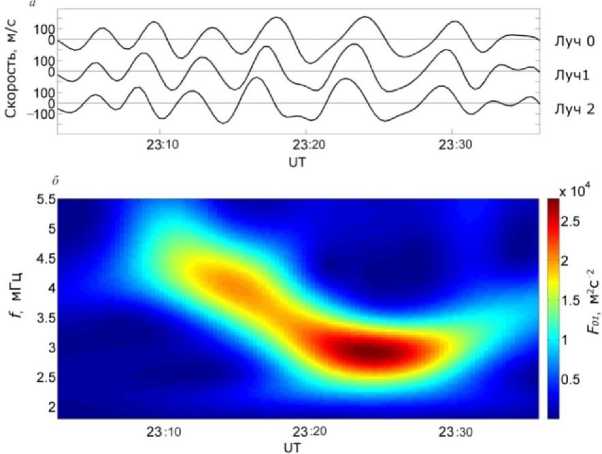
Рис. 4. Колебания скорости плазмы в области вдоль луча 0 на геомагнитной широте 59.3° ( а ), кросс-вейвлет-спектр для рядов данных, полученных вдоль лучей 0 и 1 на той же широте ( б )

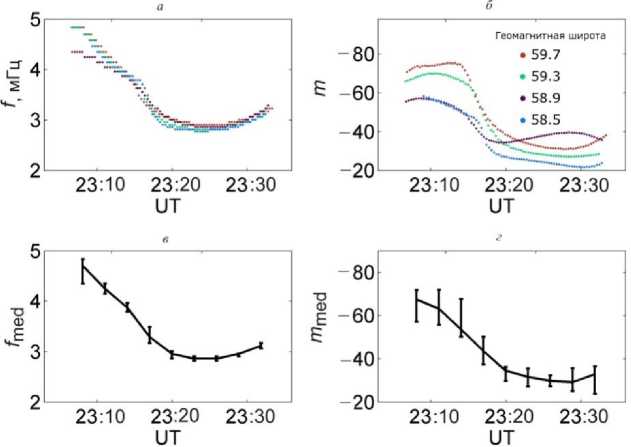
Рис. 5. Значения частоты ( а ) и азимутального волнового числа m (б ), соответствующие максимумам кросс-вейвлет -спектров на разных геомагнитных широтах, и их медианные значения ( в , г ). Планки погрешностей обозначают нижние и верхние квартили

уменьшаться и абсолютная величина m . Это указывает на изменения механизма генерации, параметров среды или на интерференцию наблюдаемой волны с каким-либо вновь возникшим волновым процессом. В рамках данной статьи мы не рассматриваем причины этого изменения в режиме колебаний. Для дальнейшего сравнения поведения частоты и волнового числа m мы используем данные, полученные во время монотонного изменения частоты в 23:06-23:25 UT.

Мы предполагаем, что для этого волнового пакета частота колебаний зависит от абсолютной величины волнового числа m . Это предположение подтверждается коэффициентом корреляции между ними, равным 0.90. На рис. 6 показана зависимость медианных значений частоты и m для рассматриваемого периода времени и диапазона широт.

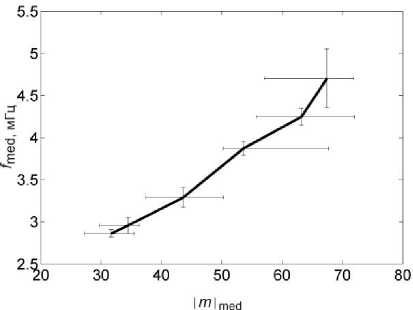
Рис. 6. Зависимость медианных значений частоты и азимутального числа m . Планки погрешностей обозначают нижние и верхние квартили

Таким образом, в отличие от МГД-волн данным УНЧ-колебаниям свойственна явная зависимость частоты от азимутального волнового числа.

Центральное значение азимутального волнового числа m ~ 50, что соответствует азимутальной длине волны 1/3 R _E (для L =5). Судя по широтной протяженности области наблюдения события, радиальная длина волны может быть оценена примерно в 1 R _E. Таким образом, это событие является примером по-лоидальных пульсаций.

ИНТЕРПРЕТАЦИЯ

В день наблюдения события геомагнитное поле было умеренно возмущенным. Межпланетная среда испытывала воздействие высокоскоростных потоков из корональной дыры CH647. Плотность солнечного ветра не превышала 8 см^–3, а его скорость менялась в пределах 400–550 км/с (рис. 7). Планетарный индекс K p достигал 4+. Однако авроральные индексы и данные наземных магнитометров указывают на значительный рост суббуревой активности. Его выз-

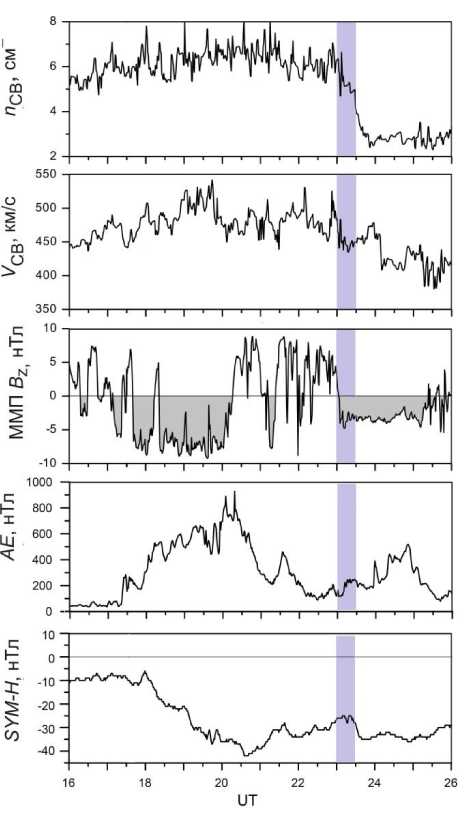
Рис. 7. Плотность и скорость солнечного ветра, вертикальная компонента ММП по данным спутника ACE, значения индексов AE и SYM-H 26 декабря 2014 г. Вертикальной полосой обозначен период времени, в течение которого наблюдались колебания скорости ионосферной плазмы

вали изменения направления межпланетного магнитного поля (ММП), которое начиная с 18:20 UT было направлено на юг в течение примерно двух часов. Это привело к постепенному росту кольцевого тока с уменьшением индекса SYM-H до –45 нТл. Зарегистрированные радаром колебания начались через час после того, как значение SYM-H -индекса достигло минимума.

Мы сравнили частоты зарегистрированных радаром колебаний с альфвеновской частотой, которую мы оценили на основе измерений магнитного поля и плотности частиц в магнитосфере. Для этого были использованы данные спутника RBSP-B (Radiation Belt Storm Probes) миссии Van Allen Probes. Высокоэллиптическая орбита спутника позволяет наблюдать параметры плазмы и поля в широком диапазоне магнитных оболочек. Примерно за 1 ч до зарегистрированного события он находился в секторе 2.5–3.8 MLT на магнитных оболочках L от 5.6 R _E до 4.2 R _E, что в проекции на Землю вдоль силовых линий соответствует геомагнитной широте от 58.87 до 55.04° и долготе от 158.36 до 158.66°. При вычислении альфвеновской частоты в секторе наблюдения события использовалось приближение дипольного магнитного поля, распределение плотности частиц было представлено в виде степенного закона n ~ r ^–α (где r — геоцентрический радиус-вектор). Таким образом, альфвеновская скорость может быть представлена как

A ( L , θ)= A eq ( L ) f A (θ),

где θ — магнитная широта,

f a (⁰) =

1+ + 3sin² 9 cos^6-a 0  ,

и A eq — альфвеновская скорость на экваторе, равная

A q ( L ) = A s/ f a ( 0 s ) , (10) где A s — альфвеновская скорость, вычисленная по измеренным спутником параметрам, а θ s — магнитная широта спутника. Имея возможность вычислить альфвеновскую скорость в любой точке вдоль заданной силовой линии, мы можем получить частоту основной гармоники. Она показана на рис. 8 как функция номера магнитной оболочки для различных значений α. На тех магнитных оболочках, на которых наблюдались колебания, альфвеновская частота находилась в пределах 13–23 мГц. Поскольку частота колебаний, которые наблюдались с помощью радара, не превышала 5 мГц, они не могут быть фундаментальной альфвеновской гармоникой.

Тем не менее частота альфвеновских мод может оказаться меньше, если учитывать конечное давление плазмы P и кривизну силовых линий κ _C . В этом случае локальное дисперсионное соотношение для полоидальной альфвеновской волны принимает вид [Klimushkin, Mager, 2015]

® A =[ k\ 2 +n] A ² ( L ) , (11) где k || — продольная составляющая волнового вектора, а η — слагаемое, обусловленное давлением плазмы:

n = 2K

4nP'

B ²

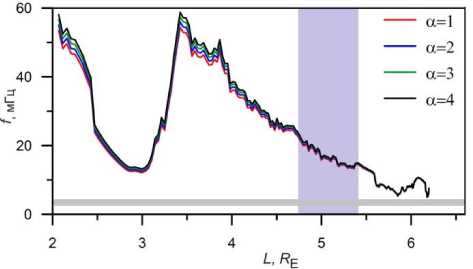
Рис. 8. Зависимость частоты главной альфвеновской моды от номера магнитной оболочки по данным спутника RBSP-B. Горизонтальной серой полосой обозначен диапазон частот колебаний, зарегистрированных радаром. Вертикальная полоса означает диапазон магнитных оболочек, в пределах которых они наблюдались

Здесь β — отношение плазменного давления к магнитному, а штрих обозначает производную по радиальной координате. Моду, описанную дисперсионным соотношением (10), принято называть альфве-новской баллонной модой. В случае больших отрицательных градиентов давления, P' < 0, частота альф-веновской волны может быть ниже, чем в холодной плазме. Однако данная волна не может быть аль-фвеновской баллонной модой, поскольку зависимость ее частоты от волнового числа m противоречит дисперсионному соотношению (10).

Складывается впечатление, что это противоречие может быть разрешено для альфвеновской моды, сгенерированной при резонансном взаимодействии волн и частиц. В этом случае частота волны также пропорциональна азимутальному волновому числу: го = m to_d, где to_d — дрейфовая частота, усредненная по баунс-траектории [Southwood, 1980]. Подобная зависимость должна существовать и для альфвенов-ских мод, излучаемых током, создаваемым дрейфующими частицами [Mager et al., 2009; Zolotukhina et al., 2008]. Тем не менее это не означает, что для приведенных случаев наблюдаемая на данной магнитной оболочке частота пропорциональна волновому числу m . Действительно, согласно дисперсионному соотношению для альфвеновской моды, ее частота Ω_A меняется только с изменением магнитной оболочки: Q 2 = k 2 A ² ( L ) . Это выражение верно и для альфвеновской баллонной моды, описываемой уравнением (10). Условие дрейфового резонанса to = m to_d заключается не в зависимости частоты от азимутального волнового числа на заданной магнитной оболочке, а в выборе оболочки, на которой может существовать альфвеновская мода: эта оболочка определяется азимутальным волновым числом [Mager, Klimushkin, 2005]. Таким образом, мы приходим к выводу, что наблюдаемую нами волну нельзя отнести ни к какому виду альфве-новских мод.

МГД-мода с частотой ниже альфвеновской — медленная магнитоакустическая мода. Однако ее частота слишком мала — на два порядка меньше альфвеновской [Leonovich, Kozlov, 2013]. Более того, вызывает сомнение применимость МГД-подхода для бесстолкновительной плазмы и низких частот, поскольку нужно учитывать баунс-движение частиц, что может быть правильно сделано только в кинетике [Hurricane et al., 1994]. Наконец, частота медленных МГД-волн определяется только давлением и плотностью плазмы и не зависит от азимутального волнового числа.

Дрейфово-зеркальная мода — еще один тип волн, для которых характерна зависимость частоты от азимутального волнового числа. Однако для их существования требуются особые условия: поперечная температура должна быть существенно выше продольной, в особенности в плазме с β<1. Не ясно, достаточно ли высока в магнитосфере температурная анизотропия.

Остается только один вид УНЧ-волн кинетической природы: дрейфово-компрессионная мода. Для ее существования в плазме с конечным давлением требуется только неоднородность плазмы в поперечном направлении. Эта волна распространяется на запад, как и протоны, дрейфующие в магнитосфере. Частота этой волны существенно ниже альфвенов-ской собственной частоты [Crabtree, Chen, 2004; Klimushkin, Mager, 2011] и зависит от азимутального волнового числа линейно [Mager et al., 2013]:

Q

м =

2 b К V

а о  Л^Vd + Vn + VT m 3 Peq________________

L          V *

L        1 - VT_

V d

Здесь l _b — длина пути частицы за один баунс-период, Λ N — собственное значение уравнения дрейфово-компрессионной моды, которое зависит от длины волны как Λ N ~ 1/λ, β eq — отношение давления плазмы к магнитному давлению на магнитном экваторе, V d — скорость дрейфа в неоднородном магнитном поле, V * и V * — дрейфовые скорости поперек магнитного поля, обусловленные градиентами плотности и температуры соответственно. Для очень больших значений m линейность должна нарушаться из-за сцепления дрейфово-компрессионных мод с альфвеновскими [Mager et al., 2015]. Линейная зависимость не действует также и для малых m , поскольку гирокинетическая теория, которая используется для получения этого соотношения, основана на условии малости длины колебаний в поперечном направлении, неприменимом для низких значений m .

Мы полагаем, что именно дрейфово-компрессионная мода является подходящим объяснением описанного в работе события. Во-первых, рассматриваемая волна распространялась на запад, что характерно для этой моды. Во-вторых, анализ данных радара, проведенный в работе, показал положительную корреляцию между частотой и азимутальным волновым числом m. В-третьих, ее частота значительно ниже собственной альфвеновской частоты на магнитных оболочках, на которых она наблюдалась, и соответ- ствует по величине дрейфово-компрессионной моде. Основываясь на уравнении (11) для основной гармоники на магнитной оболочке L=5, при условии малого градиента давления плазмы, βeq=0.2, и температуре протонов 1 кэВ можно оценить частоту дрейфовокомпрессионной моды в 0.05m [мГц], что соответствует параметрам волны.

Таким образом, мы можем заключить, что дрейфово-компрессионная мода является наиболее подходящим объяснением УНЧ-волны, описанной в работе.

ЗАКЛЮЧЕНИЕ

В работе представлен анализ колебаний скорости ионосферной плазмы, зарегистрированных среднеширотным когерентным декаметровым радаром и вызванных магнитосферными пульсациями диапазона Pc5. Событие наблюдалось на фоне умеренно возмущенных геомагнитных условий в узком долготном секторе в ночной ионосфере. Пульсации возникли под влиянием значительной суббуревой активности. Наблюдаемый волновой пакет распространялся в азимутальном направлении и представлял собой суперпозицию гармоник с частотами от 2.5 до 5 мГц и волновыми числами от 20 до 80.

Значение наименьшей частоты альфвеновской моды, смоделированное на основе спутниковых данных, оказалось существенно выше частоты зарегистрированной волны. Кросс-вейвлет-анализ рядов данных выявил зависимость частоты от азимутального волнового числа m . После рассмотрения возможных причин события мы пришли к выводу, что рассматриваемую волну следует относить к дрейфово-компрессионной моде. Совпадение направления распространения волны с направлением дрейфа протонов также подтверждает предположение о кинетической природе волны. Главным же аргументом в пользу того, что волна относится к дрейфовокомпрессионной моде, является положительная корреляция частоты и азимутального волнового числа m .

В большинстве работ, посвященных радарным исследованиям УНЧ-волн с большими m , не ставилась цель найти подобную корреляцию. В работах, описывающих большое количество событий, зависимость f ( m ) видна и для альфвеновских мод [Southwood, 1980], и для волн, излучаемых инжектированными в магнитосферу частицами [Mager et al., 2009]. Однако она проявляется вследствие того, что события наблюдаются на разных магнитных оболочках. Таким образом, путем статистических исследований не могут быть найдены доказательства существования дрейфово-компрессионной моды в магнитосфере. В работе [Mager et al., 2015] найдена зависимость f ( m ) для отдельного события, но оно, вероятно, представляло собой результат взаимодействия двух волновых мод, и поэтому затруднительно дать ему однозначную интерпретацию. Мы полагаем, что в данной работе приводятся наиболее убедительные из доказательств существования в магнитосфере дрейфово-компрессионной моды.

Конечно, это не означает, что все пульсации диапазона Pc5 с большими m следует относить к этой моде. Вероятно, большинство таких волн, наблюдаемых с помощью радара, представляют собой основную или вторую гармонику альфве-новских волн с полоидальной поляризацией [Fenrich et al., 1995; Yeoman et al., 2012; James et al., 2013].

Работа выполнена в рамках гранта № НШ-2942.2014.5 Президента РФ государственной поддержки ведущих научных школ РФ и при поддержке гранта РФФИ № 14-05-00588-a.