Начальная конфигурация дислокационного источника во втором цикле действия и локализация кристаллографического скольжения

В [1, 2] имитирован процесс действия дислокационного источника в поле препятствий дислокационной природы и отмечено, что в 73,6% проведенных экспериментов движение дислокации-источника после прохождения ею конфигурации потери устойчивости приводит к самопересечению конфигурации с отделением замкнутой расширяющейся планарной дислокационной петли, восстановлению источника и началу второго цикла его действия. Отделение первой петли от дислокации - источника и восстановление источника происходят одновременно в результате одного события - аннигиляции движущихся навстречу друг другу участков первой замкнутой дислокации, имеющих противоположное направление дислокационной оси.

В момент восстановления дислокация-источник обладает некоторой кинетической энергией, приобретенной в первом цикле действия источника Кроме того, дислокация приобретает дополнительную кинетическую энергию в процессе ее перехода из начальной конфигурации (соответствующей моменту восстановления) в конфигурацию потери устойчивости. Это одна их главных причин локализации кристаллографического скольжения (вслед за испусканием первой замкнутой дислокации источник испускает «по инерции» еще несколько петель), чему и посвящена настоящая работа.

Модель

Модель и ее алгоритмизации для имитации зарождения и распространения элементарного кристаллографического сдвига в плоскости, содержащей случайно расположенные препятствия с дискретным набором прочностей, описана в [3]. Ряд эффектов, сопровождающих распространение элементарного кристаллографического скольжения, обнаруженных в этой модели, рассмотрен в [2, 4-6]. Здесь же анализируются конфигурации восстановленных источников.

Геометрические характеристики восстановленных источников

Величина динамической локализации скольжения в значительной мере определяется "геометрией" конфигураций потери устойчивости источника в первом цикле его действия и дислокации-источника второго цикла в его начальной конфигурации. Геометрические характеристики конфигураций потери устойчивости сегментом-источником и соответствующие критические конфигурации приведены в [2], поэтому остановимся на втором вопросе.

Имитация действия источника в поле препятствий дислокационной природы позволяет выделить момент замыкания дислокационной конфигурации и, тем самым, момент восстановления дислокационного источника. Всё наблюдаемое в ЭВМ-экспериментах многообразие восстановленных конфигураций дислокационных источников укладывается в три группы (рис. 1) конфигураций, оставшихся после замыкания сегмента-источника в дислокационную петлю: 1) по классическому механизму; 2) по спиральному механизму и расположенных в среднем ниже точек закрепления источника; 3) расположенных в среднем выше точек закрепления сегмента-источника.

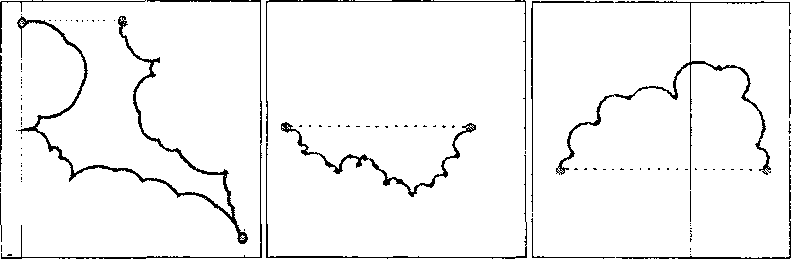
Рис. 1. К классификации начальных конфигураций дислокаций-источников при их повторном старте

Результаты моделирования показывают, что конфигурации дислокаций-источников во втором цикле действия и, следовательно, их периметры и площади варьируются в весьма широких пределах. Периметр дислокации-источника во втором цикле действия может превышать длину первоначального сегмента-источника более чем в 130 раз, периметр критической конфигурации - в 84 раза и периметр конфигурации потери устойчивости источника - в 71 раз. Периметры восстановленных источников тесно связаны с площадями, между положениями дислокаций-источников в первом и во втором циклах действия. Но есть одна особенность. При подсчете кинетической энергии дислокационной конфигурации важно, как относительно сегмента-источника расположена дислокационная конфигурация: выше или ниже. Поэтому подсчет указанных площадей проводится в системе координат с осью абсцисс, направленной по сегменту' -источнику (не важно, в какую сторону), а ось ординат - перпендикулярно вниз. При таком выборе системы координат знак "минус" у площади указывает, что она расположена, в среднем, выше первоначального положения сегмента-источника.

Проведенный анализ показывает, что размеры восстановленных источников, в среднем, больше в случае, когда дислокационные конфигурации замыкаются в дислокационные петли по классическому механизму. Статистический анализ позволяет этот эмпирический факт выразить в количественной форме. Анализ корреляций рассматриваемых признаков показал, что геометрические параметры восстановленных дислокационных источников зависят от механизма образования дислокационных петель и не зависят ни от длины сегмента-источника L в первом цикле действия, ни от напряжения старта r_$t . Наблюдаемая значимая корреляция между площадью дислокационной петли в момент её отделения от источника и площадью между положениями источников в первом и во втором циклах действия, подсчитанная по всем проведенным экспериментам, ещё усиливается для экспериментов с классическим механизмом замыкания и становится незначимой для спирального.

Источники, сгенерировавшие дислокационные петли по спиральному механизму, после восстановления "чувствуют" длину исходного сегмента-источника (коэффициент корреляции между длинами восстановленного и исходного источников для этой группы 0,733 (значим при уровне значимости а =0,05)). Например, для периметра с хорошей точностью эта зависимость может быть представлена в виде

P/L = \ 33+0,009Z*, £*6/2-^197,                     (1)

со средним значением {Р}_стр ®1,415£ .

То есть, восстановленные дислокационные источники после отделения петель по спиральному механизму невелики: по периметру они примерно в полтора раза превышают соответствующие длины сегментов-источников в первом цикле действия, что почти совпадает с периметрами критических конфигураций (P_cr = (k/2)L = \,51L') и составляет примерно 0,73 периметра конфигураций потери устойчивости

В случае классического механизма замыкания дислокационных конфигураций соответствующие показатели на порядок величины больше:

(Р\   = 13,42, (Р / Р\ = 7,23.

Зависимость превышения длины восстановленного источника по отношению к периметру конфигурации потери устойчивости сегмента-источника в первом цикле действия становится значимой и имеет вид

(jP / P )   = 11,9-0,612*, L* £72 + 197                            (2)

вместо

(^L^⁰-99-0,03 2*. L*e[2^9]              (3)

для спирального механизма. Соотношение (3) слабо зависит от длины источника и может быть переписано в виде \Р / Р )    = 0,73 .

\        у / спир

Динамическая локализация кристаллографического скольжения

Оценим величину динамической локализации скольжения в линии (зоне) скольжения, связанной с активностью единственного источника. Пусть площадь, заметаемая дислокацией-источником при переходе из его исходной конфигурации в конфигурацию потери устойчивости в первом цикле, равна Д(2 Силы, обусловленные внешним напряжением и линейным натяжением дислокации, совершают работу против сил «сухого» (примесного, решеточного, дислокационного) трения и сил «вязкого» (фононноэлектронного) трения, а также производят точечные и линейные деформационные дефекты (вакансии, межузельные атомы, дислокационные диполи вакансионной и межузельной природы). Кроме того, под действием этих сил изменяются конфигурационная (U) и кинетическая (Е,.) составляющие полной энергии (2) дислокации-источника

Полная работа, совершаемая силами Пича-Келера, обусловленными внешним напряжением (полная работа внешних сил), равна, таким образом,

А — Ад + А _г + A, + MJ + АЕ^,                               (4)

здесь А_; - работа, затрачиваемая на производство точечных дефектов при кристаллографическом скольжении,

А_к - работа, совершаемая против сил сухого трения,

A_R = T_RbbQ,                                              (5)

A_f- работа против сил вязкого трения,

Af^BuM,^Q«=^^(6)

ЕЕ и ЕЕ_к - изменения, соответственно, конфигурационной и кинетической энергии дислокационной конфигурации:

ЕЕк=Е^-Е^\(7)

EU = U№-U№.(8)

Верхние индексы (0) и (с) относятся, соответственно, к конфигурации дислокации-источника в момент восстановления и к конфигурации потери устойчивости источника в первом цикле действия.

Оставляя в уравнении для изменения кинетической энергии лишь силы дислокационного трения, поскольку именно эти силы учитываются в осуществляемой в настоящей работе имитации распространения элементарного кристаллографического скольжения, для изменения кинетической энергии находим

ЕЕ. = (т - tr )ЬЕО - UM +    .

Поскольку сегмент-источник в начальной конфигурации второго цикла его действия обладает некоторой кинетической энергией Е^, из (9) и (7) следует

Е^ = Е^ + (r- rR)bEQ-Uw + Um,(10)

или

Е^ = Е^ + (г- rR)bEQ-E0(L^-L№Y(11)

Здесь Е_о - энергия покоя единицы длины дислокации, £’^с) и Ь^№ - периметры конфигураций потери устойчивости источника в первом цикле и в момент восстановления, соответственно.

Полная кинетическая энергия дислокации-источника в процессе производства второй, третьей и последующих петель, в предположении неизменности конфигурации потери устойчивости источника в разных циклах действия, может быть представлена в виде

Е^ = Е^ +(т-г_К-г,)bEQ - Е_о (12) где т,Ь - сила сопротивления движению дислокаций, обусловленная обратными полями напряжений дислокаций, ранее испущенных источником.

С увеличением номера дислокации, испускаемой источником, напряжение т, обратного поля раннее произведённых дислокаций возрастает, при некотором п-м прохождении конфигурации потери устойчивости кинетическая энергия дислокации-источника будет равна нулю, и действие источника прекратится. Дальнейшая генерация дислокаций источником будет возможна только при повышении внешнего напряжения. Число и удовлетворяет условию

Е'^ + (г- т_К - т,^)Ь • EQ + E₀EL = 0,                     (13)

где AZ. = L^№ - L^ . Производство замкнутых дислокационных петель источником прекратится, когда напряжение обратного поля ранее испущенных дислокаций достигнет вблизи источника величины

, ,         ^0) £0 EL

А R ЬШ b EQ                          ;

Чтобы оценить величину эффекта динамической локализации кристаллографического скольжения, связанного лишь работой сил внешнего напряжения, натяжения и динамического трения только на площадке А0, предположим, что кинетическая энер- гпя сегмента-источника в момент замыкания равна нулю, ЕД = 0. Тогда уравнение

(14) принимает вид

Tj ( п)- т — тр

Ео EL

+ b XQ

Обратное напряжение, создаваемое скоплением дислокаций у границы скольже

ния, может быть представлено соотношением [7]:

. . Gbn 2 ~ v 2 т/п) =-------,

2л 2C1-VJ D

2-v

где D - диаметр области кристаллографического скольжения (зоны сдвига [8]), связанной с активностью источника, v - коэффициент Пуассона. Из (15) и (16) следует

_ 1-v п = 2л--

2-v

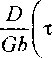
Е, ЫД b А0/

Однажды активированный дислокационный источник вслед за первой дислокацией производит в едином процессе серию замкнутых планарных расширяющихся дислокаций. Существует, следовательно, эффект локализации кристаллографического скольжения, обусловленный его дислокационно-динамическими свойствами. Такая динамическая локализация происходит при деформации скольжения во всех кристаллических материалах, то есть является неотъемлемым свойством кристаллографического скольжения. Неудивительно поэтому, что кристаллографические скольжения со значительными величинами смещения в линиях были обнаружены на многочисленных материалах самой различной природы [9-14].

Запишем выражение (17) для числа дислокаций и, производимых однажды активированным источником в виде п = ri, + п2,                                                            (18)

где и, = 2л -----\D--

Gb и2 = 2л

1р .° .

/' Gb2 EQ

Число дислокаций, произведённых источником за время его действия, считая от первой дислокации, задержанной барьерным комплексом, пропорционально диаметру D области кристаллографического скольжения. Кроме того, локализация скольжения, связанного с активностью одного источника, зависит от характеристик его конфигураций замыкания и потери устойчивости. Слагаемые в (18), представленные равенствами (19) и (20), соответствуют двум различным причинам динамической локализации скольжения. Первая из этих причин связана с конфигурацией потери устойчивости. Кристаллографическое скольжение и сопряженное с ним размножение дислокаций происходит под действием напряжения старта г„ дислокационного источника, при котором была пройдена конфигурация потери устойчивости, следовательно, в (19) можно принять т = г,, и п, = 2л ——

(2-v

I Gb

Вклад п, в общее число дислокаций, произведённых источником, определяется вкладом т^1 в напряжение прохождения конфигурации потери устойчивости, обусловленным силами линейного натяжения, которые действуют в конфигурации при кон- кретных числе, составе и расположении находящихся с ней в контакте дискретных стопоров.

Соотношение (20) для типичных значений а и Вг [16] через безразмерные площади и периметры исследуемых конфигураций принимает вид пг «100 л - —, .                                            (22)

Оно описывает вклад в динамическую локализацию, обусловленный изменением длины дислокации-источника при ее переходе из начальной его конфигурации, возникающей при замыкании первой петли, в конфигурацию потери механической устойчивости в первом цикле действия источника. Величина этого вклада определяется "геометрией" конфигураций потери устойчивости и восстановленного источника и преимущественно зависит от исходной конфигурации источника во втором цикле. Как показали выше изложенные результаты имитационного моделирования, эта конфигурация варьирует в весьма широких пределах, что может быть одной из причин значительной дисперсии величины локализации кристаллографического сдвига в следах скольжения [14]. Вклад п₂ в динамическую локализацию кристаллографического скольжения зависит от отношения АЛ / А0 и, следовательно, определяется конфигурацией дислокации-источника как в момент замыкания, так и в момент потери устойчивости. При этом доминирующим фактором является протяжённость конфигурации восстановленного источника, которая варьирует от источника к источнику в очень широких пределах и в гораздо большей степени, чем конфигурации потери устойчивости. Поэтому именно конфигурации дислокаций-источников в момент их восстановления являются основным фактором, от которого зависит вклад п₂ в динамическую локализацию скольжения. Для большинства источников, исследованных в имитационном компьютерном эксперименте, отношение tsLI NQ положительно. В этом случае силы линейного натяжения дислокации-источника при его движении на площадке \О, заключенном между названными конфигурациями, вносят дополнительный вклад в динамическую локализацию кристаллографического скольжения. Однако, хотя и в редких случаях, оно может быть отрицательным, если периметр конфигураци дислокации-источника во втором цикле действия окажется меньше, чем длина конфигурации потери устойчивости первоначального сегмента-источника.

Зависимости (21) и (22) построены по результатам машинных экспериментов и приведены на рис. 2. На фрагменте а рисунка «₁ - вклад в динамическую локализацию за счет вклада в напряжение старта источника сил, обусловленных силами линейного натяжения в конфигурации потери устойчивости (кривая, помеченная стрелкой, - приближение континуальной модели [17], нижняя кривая - данные моделирования); б - п₂ - вклад в динамическую локализацию, обусловленный разницей "геометрий" конфигураций потери устойчивости и восстановленного источника; в - «-суммарная динамическая локализация (цифры - кратности экспериментальных точек, о - классический, • - спиральный механизмы); г - зависимости и₂ /гц от длины сегментов-источников, действующих по классическому механизму На рис.З приведены распределения величины динамической локализации кристаллографического скольжения.

Обсуждение результатов

Приведенные данные показывают, что :

• 1)    континуальная модель хорошо описывает вклад («^ в динамическую локализацию кристаллографического скольжения, обусловленную силами линейного натяжения в

конфигурации потери устойчивости сегментом-источником и совсем неудовлетворительно вклад и2. Причина состоит в том, что в континуальной модели конфигурация потери устойчивости и критическая конфигурация отождествляются. Такое приближение, как показывают результаты имитационного моделирования, вполне приемлемо. При подсчете же вклада за счет разницы конфигураций потери устойчивости и восстановленного источника оценки Аб и АС* оказываются довольно грубыми, они не учитывают индивидуальных особенностей развития событий в отдельно взятых экспериментах;

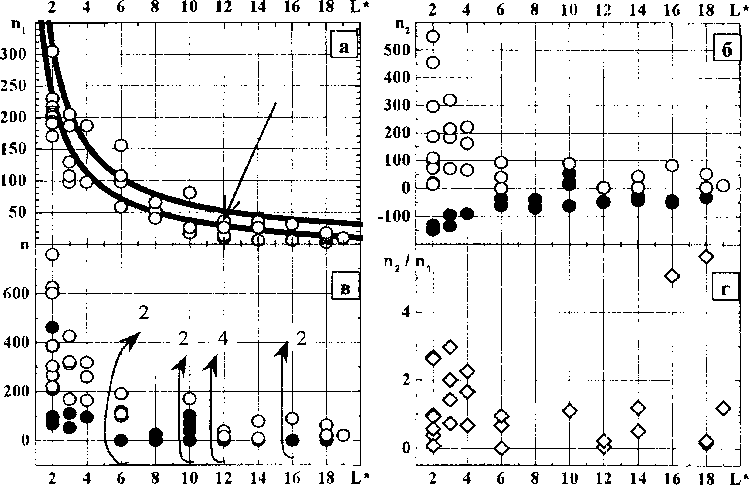
Рис. 2. К динамической локализации кристаллографического скольжения

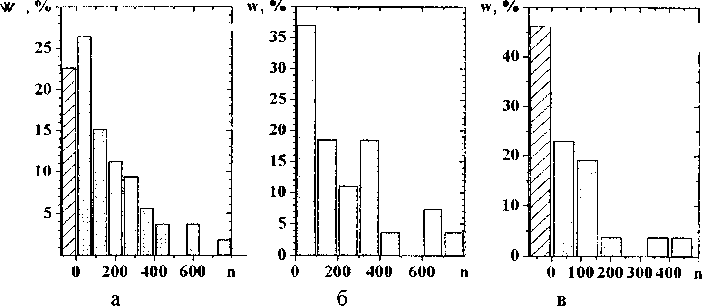
Рис 3. Распределение величины динамической локализации кристаллографического скольжения; а - все данные, б - данные для экспериментов с классическим механизмом замыкания, в - спиральным Столбцы с линейчатой штриховкой отвечают экспериментам, з которых не наблюдалось локализации

• 2)    вклад и, в динамическую локализацию не "чувствует" механизма замыкания сегмента-источника в дислокационную петлю;

• 3)    вклад п₂ различен для классического и спирального механизма замыканий: в последнем случае он значительно меньше, более того, kL (разница периметров конфигураций восстановленных источников и соответствующих конфигураций потери устойчивости) только в случае спирального механизма замыкания может быть отрицательной;

• 4)    около половины источников (46,1%), действующих по спиральному механизму, не дают динамической локализации. Если учесть, что потенциально возможные сегменты-источники действуют как источники Франка-Рида в 73,6% экспериментов, а классический и спиральный механизмы примерно равновероятны [1], то динамическая локализация наблюдается немногим более чем в половине экспериментов (56,9%);

• 5)    динамическая локализация довольно велика в отдельных экспериментах на коротких сегментах-источниках (преимущественно за счет п_л \ значительно меньше или отсутствует для длинных источников;

• 6)    учет реакции аннигиляции среди стопоров дислокационной природы в плоскости кристаллографического скольжения несколько снижает динамическую локализацию.

Разумеется, полученные величины п,п_л,п_г , характеризующие динамическую локализацию, завышены, поскольку не полностью учтены силы торможения Наиболее важной представляется отсутствие в модели сил торможения скользящих дислокаций, обусловленных производством при кристаллографическом скольжении деформационных точечных дефектов. Влияние этих сил на величину динамической локализации кристаллографического скольжения оценено в континуальной модели [16, 17].

Имеются многие другие факторы, способствующие локализации скольжения Главным из этих факторов является то, что в реальном кристалле для активации источника (для производства первой замкнутой дислокации) требуется всегда приложение более высокого напряжения, чем в последующих циклах действия источника (при испускании второй и следующей замкнутых дислокаций).

Причины этого многообразны, почти все они могут быть сведены к одной общей. Потенциальный источник, как и любая дислокация, взаимодействует с атомами примесей, а в сплавах - с атомами матрицы и легирующего элемента, точечными дефектами, а также с дислокационной подсистемой. Результатами этих взаимодействий являются изменения в окрестности дислокации концентрации компонентов и расположения дислокаций, которые, в соответствии с принципом Ле Шаталье, уменьшают энергию взаимодействий, вызвавших эти изменения. Конфигурационная энергия кристалла в результате изменений его структуры, индуцированных присутствием дислокации (включая и дислокацию - источник), уменьшается. Конфигурационная энергия покоящегося потенциального источника ниже, чем энергия действующего сегмента-источника, следовательно, при старте источника внешнее напряжение должно совершить некоторую работу, затрачиваемую на увеличение конфигурационной энергии источника, связанное со стартом. В отсутствие дислокации-источника, изменения атомной и дислокационной конфигурации кристалла становятся энергетически невыгодными. Протекают обратные процессы, поэтому для последующих прохождений дислокацией-источником конфигурации покоя достаточны напряжения, меньшие, чем напряжение старта.

Конфигурационные изменения в окрестности дислокации в реальных кристаллографических материалах имеют разную природу Это могу быть сегрегации Коттрелла,

Судзуки, изменения в поле искажений дислокации ближнего и дальнего атомного порядка, смещения дислокаций, приводящие к образованию дипольных, квазидипольных конфигураций, к дислокационным реакциям, а также встраиванию потенциального источника в конфигурации типа "стенки". Все эти и подобные им механизмы влияют на величину локализации кристаллографического скольжения, в разной степени увеличивая её. Но во всех кристаллических материалах, независимо от их чистоты и степени совершенства, имеет место динамическая локализация, которая является фундаментальным свойством кристаллографического скольжения