Начало прогрессирующего обрушения при демонтаже спортивного здания.

Демонтаж зданий обычно связан с их физическим и моральным износом. В процессе демонтажа часть сборных железобетонных конструкций может быть разобрана и в дальнейшем использована повторно. Учет при проектировании зданий и сооружений возможности их будущей разборки является экономически выгодным в долгосрочной перспективе [1], [2]. При соответствующих конструктивных решениях возможна разборка и повторное использование более 80% строительных материалов здания [3]. Разборка проводится в определенной нормативными документами последовательности. Преимущество разборки по сравнению со сносом состоит в существенно меньшем количестве строительного мусора. Помимо этого сокращается выброс пыли, загрязняющей прилегающие к объекту территории. Если содержание сборных элементов мало в сравнении с монолитными участками, то обычно прибегают к сносу здания. Простейшим способом сноса является подрыв ключевых элементов здания, вызывающий его прогрессирующее обрушение (ПО). Для прогнозирования процесса ПО прибегают к его моделированию. Сам процесс взрыва обычно не рассматривается, а моделируется последствие его для сооружения – ликвидация несущих элементов. В последние десятилетия активно формируются требования к защите зданий от ПО при проектировании, которые также предполагают моделирование удаления одного несущего элемента, например, колонны, ригеля или участка стены железобетонной конструкции [4]. Наиболее критичен для каркасных зданий обычно отказ колонны, этому случаю посвящено большинство работ по моделированию ПО [5]-[11], в отдельных случаях подтверждаемому экспериментальными данными [12]-[15].

В [16], [17] выполнены обзоры экспериментальных исследований узлов балка – колонна, балка – плита, плоских каркасных конструкций и целых зданий в контексте ПО. В работе [18] на примере каркасной конструкции апробируется метод конструктивной оптимизации и машинное обучение для проектирования железобетонных конструкций с учетом защиты от ПО.

Моделирование процесса начала ПО обычно выполняется в программах SCAD, ЛИРА, SAP2000 и др. с приближенным учетом физической и геометрической нелинейности [19], [20]. На основании критериев защиты от ПО при проектировании возможен подбор необходимого количества арматуры [21]. Как правило, колонны и ригели моделируются балочными элементами прямоугольного сечения, перекрытия - оболочечными.

Особенно важны расчеты на ПО для большепролетных спортивных сооружений из-за повышенной ответственности конструкций [22]. Если покрытие сооружения провисающего типа, повышенной надежностью должно обладать опорное кольцо. Моделирование ПО подобной конструкции показало, что при подрыве кольца собственная частота кольца и мембраны падает на 27%, высвобождается до 25% общей потенциальной энергии покрытия [23].

Железобетонные конструкции отличаются сложным многостадийным развитием разрушения. Процессы развития повреждений, как правило, изучаются на примере балок прямоугольного сечения при четырехточечном изгибе [24], [25]. Результаты расчетов сопоставляются с экспериментальными данными [26]-[29] и с формулами, приведенными в нормативных документах [30]. Для моделирования используются программные комплексы, в которых отлажены методики моделирования бетона объемными конечными элементами с учетом физической нелинейности и снижения жесткости при образовании трещин. Специальные конечные элементы позволяют производить замену матрицы жесткости изотропного конечного элемента бетона на матрицу, в которой учитывается изменение жесткости элемента в направлении развития трещины.

Деформирование стали описывается диаграммой растяжения, аппроксимированной билинейной или мультилинейной зависимостью и моделью кинематического упрочнения. В качестве критерия разрушения для бетона принимаются критерии, учитывающие анизотропию его прочности, например, критерии Кулона-Мора или Друкера-Прагера [31].

Для прогнозирования развития трещин в балках может применяться расширенный метод конечных элементов и сведение к плоской задаче [32]. При невозможности использовать специальные элементы моделирование трещин и изменение жесткости материала иногда выполняется вручную [33]. Эксперименты на балках показывают, что трещины образуются во всей области действия максимального изгибающего момента, со средним шагом, не превышающим ширину балки [28], [34]. Сложные процессы трещинообразования также реализуются в областях контакта арматуры с бетоном [35].

При моделировании на стадии трещинообразования неизбежно возникают трудности, связанные со сходимостью решения даже на простых балочных моделях. В этом случае необходимо регулировать шаг приращения нагрузки, критерий сходимости и другие настройки решателя.

Из-за сложности моделирования нелинейный процесс разупрочнения бетона обычно при расчете зданий на ПО представляется упрощенно. Встроенные в комплексы процедуры расчета усилий используются для стандартных сечений колонн и ригелей каркасных сооружений. В известных работах по моделированию ПО спортивных сооружений используются балочные и оболочечные конечные элементы [22], [23]. Цель настоящей работы состоит в оценке начала ПО при демонтаже спортивного сооружения мембранного типа с нестандартным сечением опорного кольца.

2    Materials and Methods 2.1    Конструкция сооружения

Несущая конструкция спортивного сооружения состоит из колонн, опорного кольца и мембраны (рис. 1). Размеры основных элементов сооружения приведены в [36]. Колонны состоят из стальной и бетонной части, арматура колонн не моделируется. Нижние грани четырнадцати колонн, соответствующих четверти модели, жестко закрепляются. Оголовки стальных колонн не моделируются. На колонны опирается железобетонное кольцо, в котором в кольцевом направлении располагается 45 арматурных стержней диаметром 60 мм. В Guchinsky, R.V.

The onset of a progressive collapse during the deconstruction of the sports building;

радиальном направлении в местах примыкания мембраны в кольце располагаются стальные анкеры прямоугольного сечения площадью 212 см2 каждый. Мембрана состоит из металлического полотна с основной толщиной 6 мм, и увеличенной до 8 и 12 мм толщинами в области примыкания к кольцу. Мембрана выполнена в виде сферического сегмента радиусом 404 м с основанием диаметром 160 м. Крепление мембраны к опорному кольцу выполняется через 112 выпусков, сформированных эллиптическими вырезами контура мембраны, которые через пальцы шарнирно крепятся к отверстиям анкеров кольца.

Стабилизирующая система мембраны, постель, конструкции в области аэрационного фонаря [36] в основных расчетах не моделируются. Конструкция нагружается собственным весом. Мембрана дополнительно нагружается равномерно распределенной по поверхности массой постели и технологического оборудования. Общая масса мембраны составляет 2200 Т.

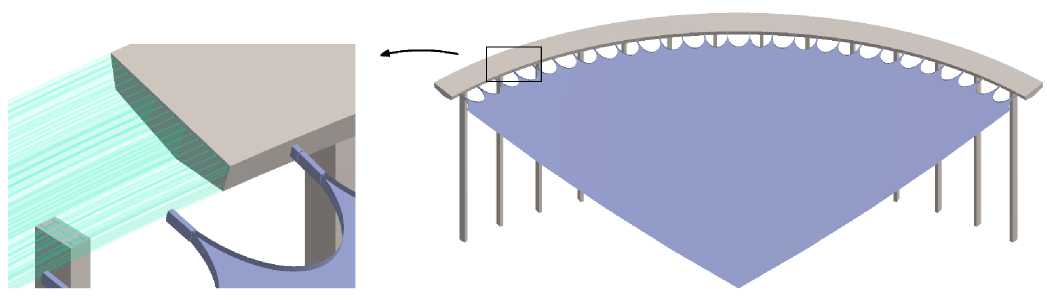
Рис. 1 - Общий вид модели четверти спортивного сооружения

Fig. 1 - General scheme of the quarter of a structure model

• 2.2    Методика моделирования и материалы

Для моделирования напряженно-деформированного состояния (НДС) конструкции используется метод конечных элементов. Все контактные взаимодействия в модели приняты жесткими, за исключением цилиндрических шарниров крепления мембраны к анкерам кольца. Мембрана моделируется четырехузловыми элементами тонкой оболочки, остальные элементы конструкции, в том числе арматура – гексаэдрическими восьмиузловыми элементами. Модель четверти конструкции содержит 1,1 млн. элементов без учета контактных элементов.

Демонтаж моделировался последовательным удалением креплений мембраны к опорному кольцу с рассмотрением эволюции напряженного состояния. При каждом следующем удалении крепления напряженно-деформированное и поврежденное состояние материала, полученное на предыдущих шагах, не учитывалось.

Основные свойства материалов, используемых при моделировании, приведены в таблице 1.

Влияние жесткости конструкций постели на оболочку мембраны учитывалось увеличением модуля Юнга стали до 5·106 МПа на основании сравнения прогибов при удалении шарнирных опор в модели с кольцевыми и радиальными элементами постели и без них. Такое упрощение связано с тем, что в расчетах не рассматривается прочность мембраны.

В расчетах не учитывалась геометрическая нелинейность. Расчет строительных конструкций на особые воздействия предполагает использование в запас идеальнопластических диаграмм деформирования бетона и арматуры [4]. В настоящей работе для уточнения момента начала разрушения учитывается упрочнение материала арматуры с помощью билинейной диаграммы деформирования, в которой участок упрочнения принимается с наклоном в 5090 МПа аналогично диаграмме деформирования арматуры A-III [39]. Задача рассматривается в статической постановке. Учет динамическгого эффекта выполняется приближенно с помощью коэффициента динамичности.

Для приближенной оценки напряжений в арматуре при демонтаже используется замена материала бетона на цилиндрически анизотропные материалы 1 и 2. Данными материалами моделируется поведение бетона при образовании радиальных трещин. Жесткость бетона уменьшается в тангенциальном (кольцевом) направлении, в остальных двух перпендикулярных Guchinsky, R.V.

The onset of a progressive collapse during the deconstruction of the sports building;

направлениях остается неизменной. Замена материала бетона на материалы 1 и 2 выполняется заново на каждом следующем шаге расчета на основании анализа напряженного состояния, полученного после удаления очередного крепления мембраны.

Предполагается, что разрушения по наклонным сечениям не происходит. Критерием начала ПО считается достижение остаточных деформаций 2,5% в арматуре [39].

Таблица 1. Физико-механические свойства материалов

Table 1. Physical and mechanical properties of materials

Материал	Модуль Юнга, МПа	Коэффициент Пуассона	Плотность, кг/м3	Нормативное сопротивление, МПа	Примечание
Бетон марки М400 (колонны, кольцо)	3·104	0,18	2300	1,75/-22	[34]
Сталь,   колонны, анкеры	2·105	0,3	7850	-	[34]
Сталь,  арматура А-II (A300)	2·105	0,3	7850	295-411	[34], [35]
Сталь, мембрана	5·106	0,3	7850	-	-
Материал 1	30/3·104/3·104	0,06/0,06/0,18	2300	-	-
Материал 2	150/3·104/3·104	0,06/0,06/0,18	2300	-	-

3    Results and Discussion

Предварительно был выполнен расчет напряженно-деформированного состояния (НДС) опорного кольца при воздействии собственного веса с учетом различных снеговых нагрузок. В данном случае конструкция и нагружения являются циклически симметричными, что позволяет рассматривать сектор конструкции размером 2π/112 рад. Рассматривались значения снеговой нагрузки с весом снегового покрова до 4 кН/м2, соответствующим максимальному нормативному весу покрова (VIII снеговой район). Коэффициент надежности по нагрузке принимается равным 1 [4].

На рис. 2 показаны поля сжимающих напряжений по сечению кольца. Характер распределения напряжений не меняется при добавлении снеговой нагрузки, так как кольцо в этом случае подвержено всестороннему сжатию так же, как и при действии собственного веса конструкции. Максимальные сжимающие напряжения, действующие на внутренней кромке кольца, при максимальной снеговой нагрузке возрастают примерно в 4,5 раза по сравнению с напряжениями от собственного веса. Во столько же раз увеличиваются и усилия, передающиеся от выпусков мембраны на анкеры. При максимальной снеговой нагрузке каждое из 112 радиальных усилий составляет 4,38 МН (рис. 3). Проводя экстраполяцию можно видеть, что разрушение бетона кольца от сжимающих напряжений может начаться только при статических вертикальных нагрузках на мембрану порядка 8 кН/м2, при этом масса нагруженной мембраны должна быть увеличена с 2200 Т до примерно 20000 Т. Определяющими прочность конструкции в этом случае могут оказаться анкеры или мембрана.

Далее приведены результаты расчета напряженно-деформированного состояния кольца при демонтаже сооружения последовательным отделением выпусков мембраны от анкеров кольца (удалением цилиндрических шарниров). Для упрощения моделирования рассматривались варианты четного количества удаленных шарниров. В этом случае возможно рассмотрение половины конструкции из-за наличия одной плоскости симметрии при деформировании. Из-за сложности конечно-элементной модели для сокращения времени расчетов была рассмотрена четверть конструкции. Формально такая схема предполагает параллельный демонтаж конструкции с двух сторон. Однако, как показывает сопоставительный расчет, при удалении до 20 шарниров результаты НДС кольца идентичны при рассмотрении четверти и половины модели из-за малого количества (меньше 18%) удаляемых шарниров, не приводящих к заметному снижению жесткости конструкции вплоть до начала ПО.

При удалении четырех шарниров КН в опорном кольце не повышаются до положительных значений (рис. 4 а ). Разрушение бетона начинается в области анкера с крайним действующим шарниром. Так как демонтаж выполняется с одной стороны, то разрушение от растягивающих напряжений ожидается у анкера с противоположной стороны из-за локализации напряжений в месте крепления анкера при несколько меньшем изгибающем моменте по сравнению с сечением плоскости симметрии (рис. 4 б ). Напряжения, действующие в арматуре, при этом не превышают 40 МПа.

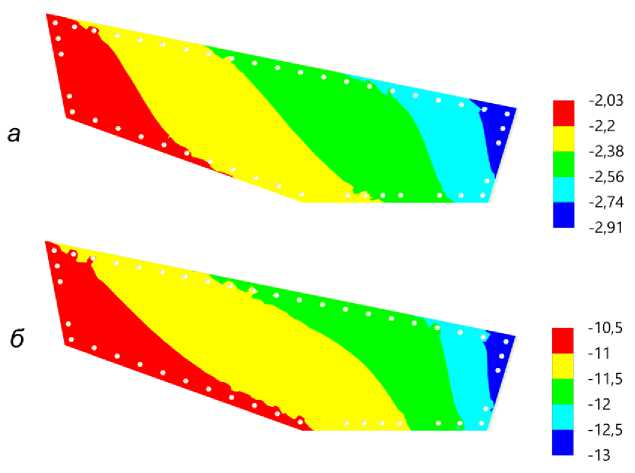
Рис. 2 - Распределение кольцевых напряжений (KН) по сечению кольца при отсутствии снеговой нагрузки ( а ) и при снеговой нагрузке 4 кН/м²( б )

Fig. 2 - Distribution of hoop stresses (HS) over the cross section of the ring in the absence of snow load ( а ) and with a snow load of 4 kN/m² ( б )

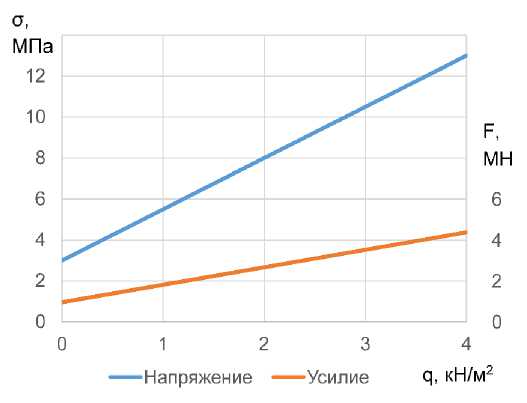
Рис. 3 - Наибольшие КН и усилия в выпусках мембраны при различной снеговой нагрузке

Fig. 3 - The maximum HS and forces in the outlets of the membrane at different snow load

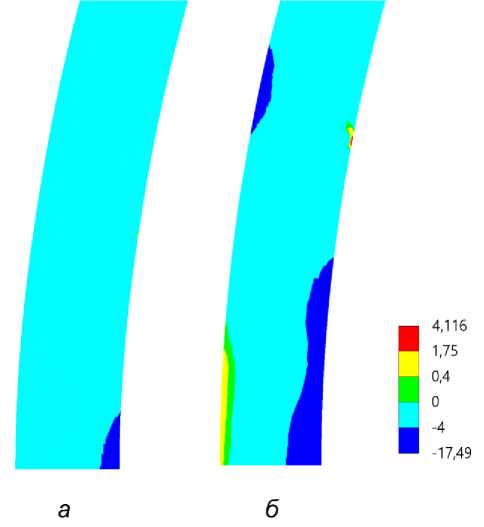
Рис. 4 - КН в кольце при удалении 4 ( а ) и 6 ( б ) шарниров (вид сверху, четверть модели), МПа

Fig. 4 - HS in the ring when removing 4 ( а ) and 6 ( б ) hinges (top view, quarter of the model), MPa

С удалением 8 и более шарниров при решении задачи без учета нелинейности бетона появляются заметные области превышения предела прочности бетона на растяжение (рис. 5). При этом арматура, жестко соединенная с материалом бетона, оказывается малонапряженной, что не соответствует действительности. Для определения напряжений в арматуре после получения решения исходного варианта (И) выполняется замена основного материала бетона на материал 1, характеризующийся модулем Юнга в кольцевом направлении 0,001Е и материал 2 с соответствующим значением 0,005Е (Е – модуль Юнга бетона). Замена выполняется для высоконапряженных блоков материала бетона таким образом, чтобы получить два ограничивающих расчетных варианта – переоценки бетона (ПБ) и недооценки бетона (НБ). После замены материала при ПБ в модели допускаются напряжения, превышающие предел прочности. Также при удалении 16 шарниров и замене материала растянутой зоны увеличивается область напряжений, превышающих предел прочности на сжатие (рис. 5, 16 ПБ). В этих областях материал не заменяется, тем самым сопротивление бетона в сжатой зоне также завышается. Во всех случаях ПБ напряжения в арматуре недооцениваются. КН в замененном материале уменьшаются на 2-3 порядка.

Замена бетона в случае НБ выполняется двумя материалами: наиболее напряженный бетон меняется на материал 1, менее напряженный – на материал 2. В этом случае КН должны быть меньше напряжений, соответствующих пределам прочности, во всех областях кольца. Например, в случае 16 НБ (рис. 5) выполняется замена всего материала в наиболее напряженных сечениях, поэтому изгибающие моменты в них практически полностью воспринимаются арматурой. Напряжения в арматуре в этом случае переоцениваются.

В штатно работающей конструкции при целостности всех шарниров изгибающие моменты в кольце отсутствуют. При последовательном удалении шарниров изгибающие моменты в основных опасных сечениях кольца существенно увеличиваются. Например, на рис. 6 показан полный изгибающий момент в сечении плоскости симметрии. При замене материала в опасных сечениях изгибающий момент перераспределяется по длине кольца. При удалении 8 шарниров из-за небольшой разрушаемой зоны бетона распределение моментов практически не меняется, на момент удаления 16 шарниров изгибающий момент в рассматриваемом сечении после замены материала уменьшается на 30%. Действительная кривая увеличения изгибающего момента лежит между кривыми для НБ и ПБ. Изгибающие моменты появляются при демонтаже только в области удаленных шарниров, в остальной части кольцо в целом сохраняет свою форму.

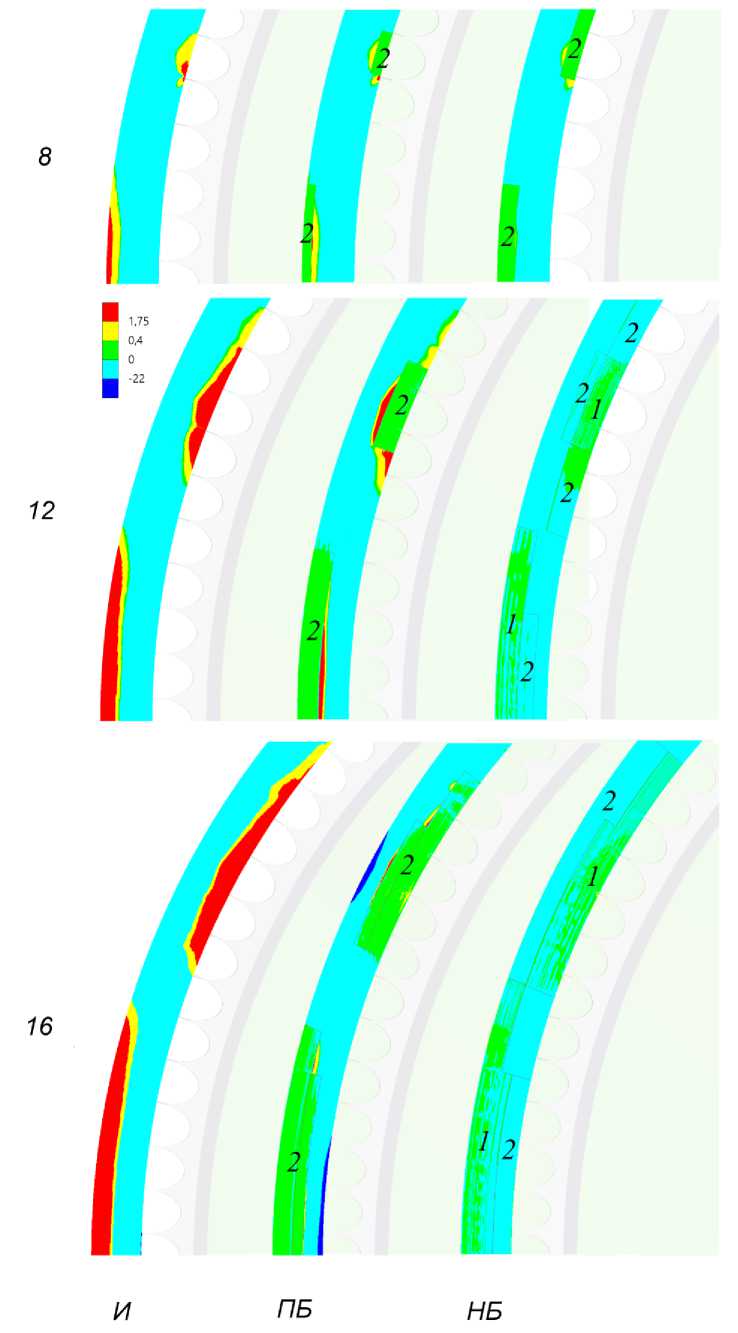
Рис. 5 - КН при замене бетона на материал 1 и 2 для исходного варианта (И), при переоценке (ПБ) и недооценке (НБ) бетона, в случаях удаления 8, 12 и 16 шарниров, МПа

Fig. 5 - ТS when replacing concrete with material 1 and 2 for the original version (И), when overestimating (ПБ) and underestimating (НБ) of concrete, in cases of removing 8, 12 and 16 hinges, MPa

На рис. 7 приведены формы деформации кольца при удалении 4, 8, 12 и 16 шарниров. Демонтаж выполняется с одной стороны. Таким образом, плоскость симметрии НДС кольца поворачивается с равными угловыми приращениями. Стрелками показаны сектора кольца с удаленными шарнирами. Положение сечения крайнего выпуска мембраны, на который приходится максимальное усилие, не меняется с одной стороны и последовательно перемещается со стороны демонтажа. Поэтому начало ПО прогнозируется в сечении с противоположной стороны от демонтажа. Положения крайних опасных сечений при ПБ на рис. 7 в несколько искажены из-за увеличенного масштаба перемещений.

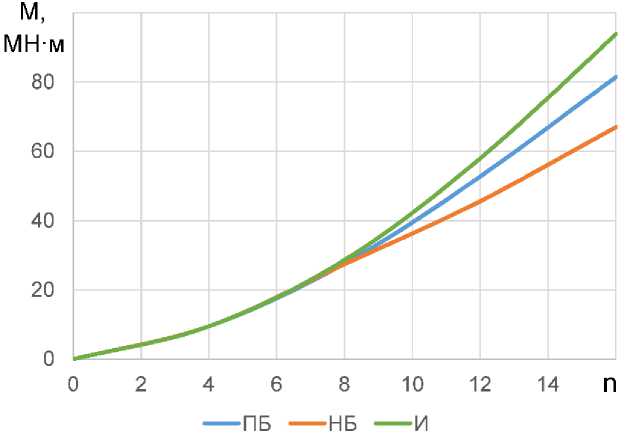
Рис. 6 - Полный изгибающий момент в сечении кольца в плоскости симметрии в зависимости от числа удаленных шарниров

• Fig. 6    - Total bending moment in the section of the ring in the plane of symmetry depending on the number of removed hinges

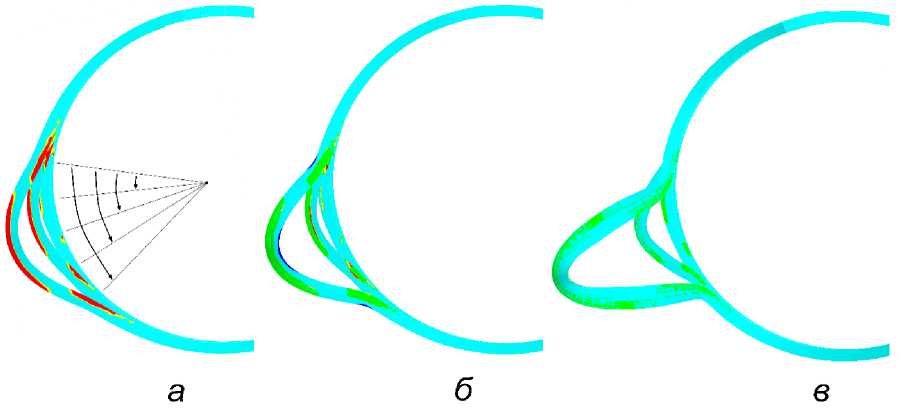
Рис. 7 - Схема деформации кольца и поля КН при последовательном удалении шарниров в исходном случае ( а ), при ПБ ( б ) и НБ ( в ), масштаб перемещений 1:100

• Fig. 7    - Schematic diagram of the deformation of the ring and the PT field with sequential removal of the hinges in the initial case ( а ), in the case of ПБ ( б ) and НБ ( в ), the scale of displacements is 1:100

Возрастание максимальных напряжений в арматуре в процессе демонтажа показано на рис. 8. Значение напряжений в каждом случае определялось минимальной величиной напряжения, которое достигается в двух крайних стержнях арматуры в опасном сечении по длине арматуры, равной ее диаметру. Пример распределения упругих напряжений для случая

• 16 шарниров при ПБ показан на рис. 9. Эти значения получены без учета физической нелинейности арматуры. При использовании билинейной кривой деформирования арматуры пластическая деформация зависит от числа удаленных шарниров и рассматриваемой модели бетона. В случае 16 шарниров для любых модели бетона и предела текучести арматуры пластическая деформация меньше 2,5%, при 20 удаленных шарнирах – больше этого значения в большинстве случаев.

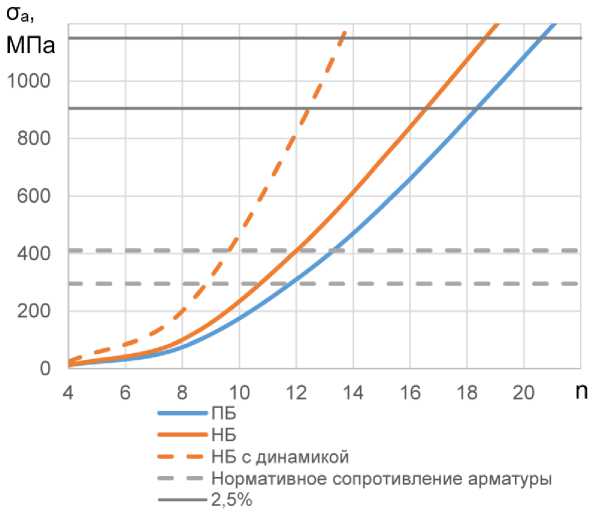
Рис. 8 - Максимальные напряжения в арматуре при различном числе удаленных шарниров, МПа

Fig. 8 - Maximum stresses in the reinforcement with a different number of removed hinges, MPa

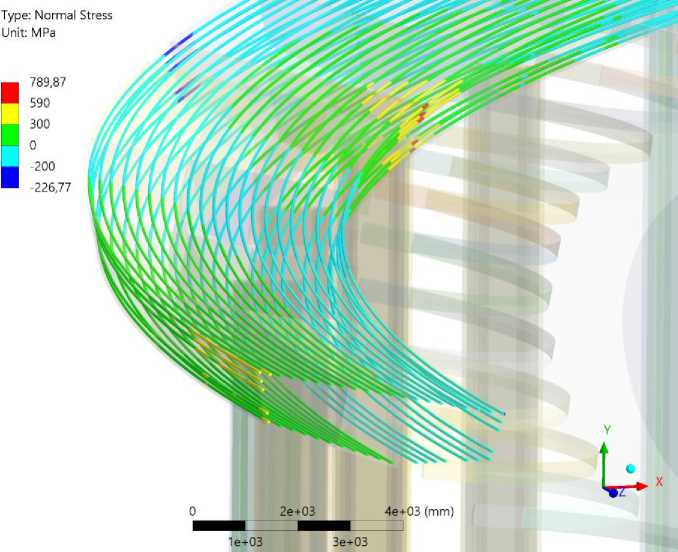
Рис. 9 - Распределение нормальных напряжений в арматуре при удалении 16 шарниров, случай ПБ

Fig. 9 - Distribution of normal stresses in reinforcement when removing 16 hinges, case of ПБ

Для определения диапазона критических упругих напряжений, соответствующих пластической деформации 2,5% при решении нелинейной задачи, было выполнено несколько расчетов с учетом физической нелинейности арматуры. Данные значения напряжений для экстремальных значений предела текучести в генеральной совокупности арматуры класса A-II, показаны на рис. 8 горизонтальными сплошными линиями. Использование результатов решения упругой задачи позволяет отобразить результаты, полученные в диапазоне от небольших упругих деформаций арматуры до развитых упругопластических. С помощью решения в упругой постановке приближенно может быть определена стадия демонтажа, начиная с которой необходимо рассматривать нелинейность стали. Нижняя граница диапазона критических упругих напряжений арматуры получена при рассмотрении случая НБ и удалении 16 шарниров для материала арматуры с минимальным пределом текучести. При решении упругопластической задачи определялся коэффициент увеличения вертикальной нагрузки (не более 1,2), при котором пластическая деформация в арматуре достигала 2,5%. Затем при полученной нагрузке выполнялось упругое решение, и определялись критические упругие напряжения в арматуре. Верхняя граница критических напряжений получена аналогично для случая ПБ при удалении 20 шарниров и при наибольшем значении предела текучести арматуры в генеральной совокупности. Из-за ограниченной области пластических деформаций арматуры напряжения в замененном материале бетона увеличиваются незначительно при учете физической нелинейности арматуры, вызывающем дополнительное локальное догружение бетона. При этом статус материала бетона (НБ или ПБ) не меняется.

На рис. 8 значения абсцисс графика (число удаленных шарниров) являются дискретными, поэтому предполагается, что разрушение арматуры наступает при числе удаленных шарниров, которое получается округлением до целого в большую сторону абсциссы пересечения кривой напряжений с линией критических напряжений арматуры. Разрушение при отсутствии учета динамического эффекта ожидается при удалении 17-21 шарнира.

Последовательное удаление шарниров вызывает быстрый рост усилий в крайних шарнирах (рис. 10). При целостности всех шарниров усилие в каждом составляет 0,96 МН (рис. 3). При удалении 6 шарниров усилие в наиболее нагруженном шарнире превышает 5 МН. Соответственно, удаление 6 шарниров в конструкции сооружения без снегового покрова примерно эквивалентно по нагружению шарнирного крепления нормативной снеговой нагрузкой для VIII снегового района. С учетом того, что разрушение конструкции не может произойти раньше удаления 13-го шарнира, усилие, приходящееся на анкер при разрушении кольца, составляет не менее 13 МН. Стоит отметить, что большие отличия усилий в первом и втором шарнирах создают предпосылки для локального упругопластического деформирования области крепления крайнего шарнира и некоторого перераспределения усилий на несколько соседних шарниров.

Возмущающее воздействие удаления шарниров не распространяется дальше пяти крайних шарниров. Это подтверждает возможность использования четверти модели вместо ее половины, так как четверть модели содержит 28 шарниров, в то время как влияние демонтажа конструкции не распространяется дальше 15-ти шарниров от плоскости симметрии.

В процессе удаления шарниров происходит резкий обрыв связи выпусков мембраны и анкеров, что приводит к ударной нагрузке на шарниры и опорное кольцо. Учет динамической составляющей нагрузки в данном случае затруднен из-за множества неопределенных факторов, например, динамических характеристик кольца и мембраны, времени действия ударной нагрузки, повышения прочности материалов при динамическом воздействии. Значения напряжений в бетоне и арматуре в данном случае сильно зависят от демпфирующих свойств материалов и конструкции в целом, определение которых является трудоемкой задачей.

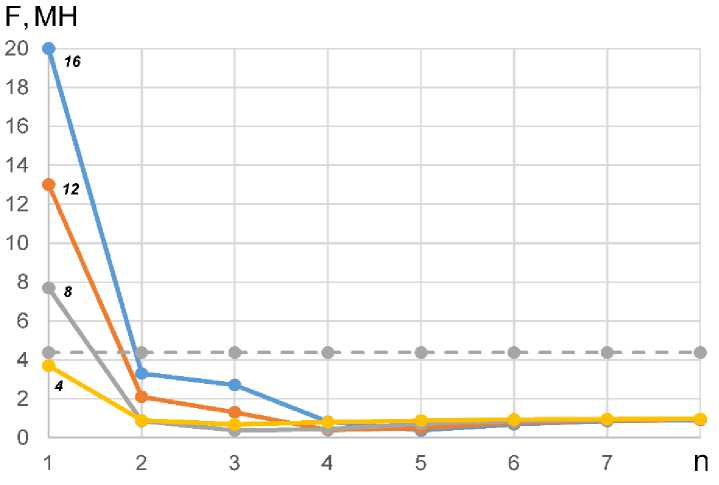
Рис. 10 - Усилия в крайних восьми шарнирах при удалении 4, 8, 12 и 16 шарниров, штриховая линия – усилие в шарнирах для нормативной нагрузки VIII снегового района, модель ПБ

Fig. 10 - Forces in the last eight hinges when removing 4, 8, 12 and 16 hinges, the dashed line is the force in the hinges for the standard load of the VIII snow region, model ПБ

При проектировании обычно предусматривают защиту от ПО, выполняя моделирование устранения одного несущего элемента конструкции [4]. В рассматриваемом примере устраняется несколько несущих элементов. Для учета динамичности процесса можно воспользоваться следующей методикой. При удалении необходимого количества шарниров вычислить усилия, действующие в крайних шарнирах. Затем рассмотреть эквивалентную статическую задачу, в которой в одном из крайних шарниров вместо разорванной между элементами связи приложены вычисленные взаимно компенсирующие усилия. При дальнейшем решении задачи методами прямого интегрирования уравнений динамики это значение уменьшается до нуля за определенный промежуток времени, равный продолжительности ударного воздействия. По отклику системы впоследствии делается вывод о динамическом эффекте на систему. Подобная методика с приложением нагрузок, найденных для первичной расчетной схемы, с обратным знаком к вторичной расчетной схеме и использованием стандартных параметров демпфирования 2-5%, регламентирована [4] и нашла отражение в некоторых современных САПР [19], [20]. С учетом сложности рассматриваемой модели сооружения решение подобной задачи может быть очень ресурсозатратным и нецелесообразным для определения трудоемкости работ при демонтаже. Известно, что максимальный коэффициент динамичности для линейно-упругой задачи при внезапном приложении нагрузки равен 2. Предполагая, что напряжения с учетом динамического воздействия для нелинейно-упругой задачи превышают статические не более, чем в 2 раза (коэффициент увеличения динамической прочности арматуры принимается равным 1 [4]), можно получить, что ПО не произойдет раньше удаления 13-го шарнира (рис. 8). Так как в расчетах не учитывается геометрическая нелинейность, можно прогнозировать, что разрушение не может произойти позже удаления 21-го шарнира. Полученные наибольшие значения перемещений кольца, не превышающие 10% размера сечения в случае НБ (рис. 7), позволяют предполагать несущественное влияние геометрической нелинейности на результаты расчета.

Приведенный ряд квазилинейных моделей условно описывает процесс начала разрушения опорного кольца. Нагружение в каждом расчетом случае выполняется одним приращением нагрузки. Более точно прогнозировать НДС кольца можно при определении нелинейных свойств бетона и арматуры, начиная с момента удаления шести шарниров. Затем, используя малые приращения нагрузки, для удаления каждого следующего шарнира расчет следует повторить с учетом деградации материала при удалении предыдущих шарниров. Однако из-за значительной дискретизации модели даже без учета динамического нагружения такой расчет является крайне ресурсозатратным.

4 Conclusions

Демонтаж несущей конструкции спортивного сооружения способом последовательного удаления шарнирных связей мембраны и опорного кольца вызывает ПО из-за разрыва арматуры с внутренней стороны кольца. При эксплуатации сооружения опорное кольцо подвергается всестороннему сжатию, которое в процессе демонтажа дополняется его локальным изгибом. Начало обрушения наступает не позже удаления двадцати одного шарнира, что составляет около 18% их общего количества. С учетом динамической составляющей нагрузки обрушение при демонтаже может произойти не ранее удаления тринадцати шарниров, без ее учета – не ранее семнадцати.

При прогнозировании момента начала обрушения рассматриваемого сооружения возможна замена нелинейного расчета рядом последовательных приближенных линейных расчетов, при которых прочность бетона занижается либо завышается. Для моделирования деградации материала бетона при возникновении радиальных трещин в осесимметричных конструкциях или конструкциях с циклической симметрией целесообразно использование модели цилиндрически анизотропного материала. Предложенный способ моделирования может применяться при планировании демонтажа спортивных сооружений.