Надежность деталей и неремонтируемых узлов при проектировании машин

Reliability of parts and unrestorable components in the machine design∗

Введение. Условия постановки на производство продукции машиностроения и единая система конструкторской документации (ЕСКД) [1–2] требуют, чтобы при разработке проекта машины учитывались следующие параметры надежности технических систем (ТС): — долговечность — календарный срок службы T k );

• —    безотказность — вероятность безотказной работы P ( t ) ...);

• —    наработка t = T часов (на этот период должна быть гарантирована ВБР).

Данные показатели согласуются на стадии технического задания (ТЗ) и характеризуют машину в целом. Разработчик должен повлиять на безотказность, которая является главным свойством надежности невос-станавливаемых ТС и в межремонтные периоды работы формирует долговечность восстанавливаемых ТС.

Наработка t является аргументом функции надежности P ( t ). По любому закону надежности P ( t ) монотонно убывает с наращиванием t . В силу этого для достижения требуемой ВБР наработка должна быть рационально минимизирована и выбрана в соответствии с логикой работы ТС [3].

Детали и невосстанавливаемые изделия, вырабатывая свой ресурс, определяют наработку системы на отказ. В идеале наработки элементов на отказ должны совпадать или хотя бы быть кратными выбранной наработке ТС. При этом календарный срок службы T k и требуемая наработка T связываются соотношением:

T = T k ⋅ 365 ⋅ K год ⋅ 24 ⋅ K сут ⋅ ПВ, ч ,                                         (1)

где T k — календарный срок службы в годах; К_год — коэффициент возможного использования ТС в год; К_сут — коэффициент использования ТС в сутки; ПВ — относительная продолжительность включения, которая представляет собой осредненное отношение времени включения (время разгона и время установившегося движения) ко времени рабочего цикла ТС.

Высокая вероятность безотказной работы (ВБР) возможна при снижении требуемой наработки. Если ее необходимо существенно увеличить, безотказность придется поддерживать следующим образом:

• —    чаще выполнять техническое обслуживание (ТО);

• —    при проектировании ключевых элементов закладывать более высокие затраты на обеспечение качества изделий [4, 5].

ВБР проекта может быть выбрана из существующих отраслевых нормативов, из конкурентных условий и по другим основаниям, в том числе из условных классов надежности, принятых для изделий машиностроения (табл. 1).

Таблица 1

Классы надежности изделий машиностроения

Класс надежности	0	1	2	3	4	5
Допустимое значение ВБР P ( t )	≤ 0,9	≥ 0,9	≥ 0,99	≥ 0,999	≥ 0,9999	1

При рассмотрении классов надежности учитываются перечисленные ниже группы характеристик ТС [3, 6, 7].

Машиностроение и машиноведение

• 1.    По структурному типу изделий. Рассматриваются технологические комплексы, машины, агрегаты, механизмы и иерархия (уровни) их сборочных единиц и деталей. При последовательном взаимодействии элементов в большинстве машин ВБР растет с переходом к нижним уровням структурной схемы надежности. Тогда ВБР деталей при структурном анализе может приближаться к показателям 3–5 классов надежности.

• 2.    По видам ТС. Планируемый уровень ВБР напрямую зависит от уровня ответственности производителя перед потребителем ТС. Безусловно, высочайший уровень ВБР планируется, например, для летательных аппаратов, машин химических производств, медоборудования, военной техники и т. п.

• 3.    По видам последствий отказов. Планируемый уровень ВБР напрямую зависит от потенциального уровня ущерба при отказе машины (экономического, экологического, репутационного и пр.).

Общепринято [5, 6, 8–13] представление отказов ТС как внезапных. В этом случае ВБР описывается экспоненциальным законом

P ( t ) = e ^{-λ t} .                                                             (2)

Здесь интенсивность отказов X в период нормального функционирования после приработки связывается со средней наработкой на отказ Т системы х = 1/T(3)

с параметрами безотказности

Х = (- ln P(T))/ T .(4)

Отсюда может быть рассчитана средняя наработка на отказ ТС

T = -T /(ln P (T)).(5)

Этот алгоритм формирования параметров надежности ТС имеет как сторонников, так и критиков [7, 10, 14]. Все ли отказы происходят внезапно? Насколько верны параметры надежности ТС (3)-(5), вытекающие из экспоненциального закона? Эти вопросы возникают при определении интенсивности отказов (4) и соответствующей ВБР ТС (3) вне зависимости от методики оценки:

— по заданным наработке T и ВБР Р ( T );

— по средней наработке на отказ Т ;

— по результатам испытаний Т .

В литературе структурный анализ надежности ТС, преобразующих входное воздействие (ВВ) в выходные параметры (ВП) принято представлять как восходящий схемный анализ от ВБР элементов к ВБР систем. При этом рассматриваются структурные схемы: последовательные (рис. 1, а ), параллельные (рис. 1, б ) и комбинированные (рис. 1, в ).

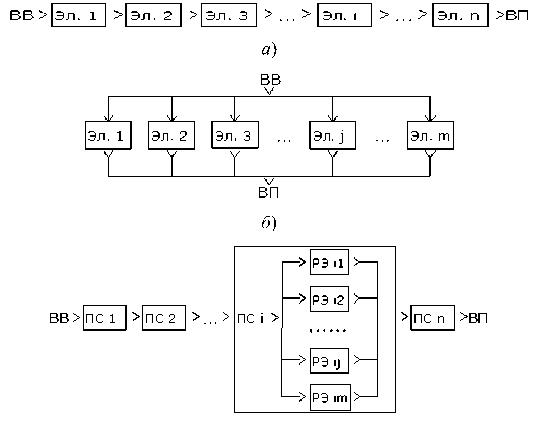
в )

Рис. 1. Структурные схемы надежности технических систем при различных видах взаимодействия элементов

При последовательном взаимодействии элементов ТС (см. рис. 1, а ), отказы которых независимы, экспоненциальный закон (2) представляет удобную математическую модель. Если ВБР системы Р ( t ) и элементов — подсистем P i ( t ) находятся в соотношении

n р (t)=П p (t),                                               (6)

i = 1

то интенсивности отказов системы X и подсистем X i находятся в соотношении n

^ = Z ^                                       (7)

г = 1

и ранжируются в зависимости от принятого принципа распределения интенсивностей по элементам.

Иерархическая структурная схема, сформированная из вложенных уровней подсистем и элементов [3, 6, 8-12], позволяет выборочно или по всей структуре выполнять нисходящий анализ [3,9] (от ВБР ТС к ВБР элементов). Требуемые значения ВБР элементов вместе с требуемой наработкой являются исходными данными для проектирования деталей с заданным уровнем надежности [15,16].

Алгоритм нисходящего анализа на базе (2) позволяет одинаково успешно распределять интенсивности и ВБР элементов по всем вложенным уровням структурных схем. Это справедливо для радиоэлектронных систем [10, 11]. Но на уровне деталей механической системы [3] возникает противоречие: нельзя применять экспоненциальный закон, если развитие постепенного отказа протекает по другому закону. Отказ системы произойдет в результате последовательного взаимодействия, не связанного с экспоненциальным законом. В то же время разработка структурной схемы надежности ТС имеет смысл, если она служит основанием для проектирования деталей и подбора стандартизованных элементов с требуемой ВБР на выбранную наработку.

При анализе ВБР ТС с параллельным взаимодействием элементов (см. рис. 1, б ) учитываются следующие условия:

— элементы включены постоянно,

— их отказы независимы,

• —    каждый из m элементов имеет ВБР P j ( t ) ,

• —    каждый из m элементов способен принять входное воздействие и преобразовать его в выходной параметр ТС (см. рис. 1, б).

В этом случае отказ ТС произойдет после отказа последнего работоспособного элемента. Вероятность отказа системы через вероятности отказов элементов:

m

F (t) = П j t>•( j=1

Из свойства

P(t) + F (t) = 1(9)

вероятность безотказной работы системы через ВБР элементов: m p (t) = 1 -П[1 - Pj( t)].(1°)

j = 1

Для однородных элементов

P(t)=1 -[1 - Pj (t) ]m.(11)

Если цель — обеспечение заданной ВБР ТС и учитываются однородные резервированные элементы, то использование выражения экспоненциального закона (2) дает простой расчет интенсивности отказов элементов или числа элементов m только в соотношении (11). Для более сложных соотношений (10) и комбинированных структур (см. рис. 1, в ) примеры использования экспоненциального закона не приводятся.

Простое разделение на элементы невозможно, если речь идет о сложных структурах с разнонаправленным взаимодействием элементов, имеющих зависимые отказы. Параметры функционирования и надежности должны определяться для системы в целом, а для этого, возможно, потребуется выполнить большой объем аналитических и экспериментальных работ. Графическое представление таких схем [7, 9] сопровождается упоминанием о сложности модели функционирования и громоздкости расчетов надежности (например, сложное замкнутое взаимозависимое функционирование блоков двигателя внутреннего сгорания или реактивного двигателя).

Основная часть. Для конструктивной реализации ТС с любым видом взаимодействия необходимо изготовить детали, из которых составляют сборочные единицы, а затем функциональные модули (механизмы, агрегаты, блоки питания, блоки управления и т. п.). Современный модульный принцип построения машин предусматривает модульные операции: разработку, сборку и отладку, модификацию и модернизацию, ремонт, замену и т. п. Детали и прочие элементы находятся на нижнем уровне иерархической конструктивной системы, состоящей из вложенных блоков. Используя ее в качестве структурной схемы надежности, необходимо найти критерий распределения ВБР по элементам. Следует рассмотреть не функцию P ( t ), а ее численное значение P ( T ). В этом случае можно подставить заданную наработку T и при распределении численных значений ВБР по элементам использовать в качестве критерия стоимости восстановления структурных единиц в случае их отказов. В стоимость восстановления могут быть включены:

Машиностроение и машиноведение

• —    стоимости используемых для ремонта материалов, изделий, диагностики и ремонтных работ;

• —    оцененные в денежных единицах последствия отказа (восстановление других отказавших элементов при зависимых отказах, потери от простоя ТС, страховые выплаты на возмещение ущерба и др.).

Задачей настоящего исследования является разработка метода нисходящего анализа структурных схем надежности, устраняющего отмеченные выше противоречия. Структурная схема надежности ТС должна быть инструментом распределения ВБР элементов по заданной ВБР ТС на начальных стадиях проекта. Тогда выбранная наработка и сбалансированные ВБР элементов будут исходными данными для проектирования с заданным уровнем надежности. Для этого структурная схема должна удовлетворять ряду условий.

• 1.    Структурная схема должна основываться на структуре конструкции. Это упростит сложные функциональные связи между элементами

• 2.    Структурная схема должна содержать математическую модель надежности, доступную для расчетов на ранних стадиях проекта.

• 3.    Модель надежности по структурной схеме должна опираться не на экспоненциальный закон, а только на фундаментальные свойства надежности технических объектов и систем (6), (8)-(11).

• 4.    Критерием ранжирования ВБР элементов должна быть стоимость восстановления элемента в случае его отказа. Ее можно рассматривать как денежный эквивалент возмещения ущерба от отказа.

• 5.    Нисходящий структурный анализ должен применяться одинаково эффективно как для последовательно взаимодействующих, так и для резервированных и комбинированных схем надежности.

Альтернативное представление численного значения ВБР объекта. Пока время t имеет значение аргумента функции безотказности P ( t ), она представляет собой функцию, убывающую по любому из известных законов или полученную статистическим путем. После выбора требуемой наработки t = T ВБР получает значение P ( t ) = P ( T ) в границах 0 <  P ( T) <  1. Такое число может быть представлено множеством способов, из которых выбирается показательное выражение

P(T) = BX.(12)

Х определяется из соотношения

X = lg (P(T)) / lg B.(13)

Приняв значение основания степени В = 10, получим выражение численного значения ВБР:

P (T) = 10X,(14)

откуда

X = lg P (T).(15)

Показатель степени X назовем параметром ранжирования (ПР) ВБР ТС. В приложении к элементам системы показатели степени X i также именуются параметрами ранжирования ВБР элементов. Далее в этом представлении рассматривается «самый простой и самый важный случай» [13] надежности систем.

ВБР элементов ТС при их последовательном взаимодействии. Рассмотрим структурную схему надежности ТС с последовательным взаимодействием элементов (см. рис. 1, а ), отказы которых независимы. В этом случае отказ системы при отказе любого из n элементов в момент времени t = T выражается через ВБР элементов согласно (6):

n P ( T ) = П P ( T ). i = 1

В (6) произведение может быть получено множеством комбинаций P i (T ) и видов их представления. Применив (14) для численных значений ВБР системы P ( T ) и ее элементов, произведение P ( T ) = P 1 ( T ) х P₂(T ) х ... х P n ( T ) можно представить:

• 10 ^X = 10 ^{X 1} х 10 ^{X 2} х ... х 10 ^Xn , откуда связь ПР системы и элементов:

X = X , + X ₂ + ... + X_n.                                       (16)

Из множества возможных комбинаций X i в (16) выбираются вытекающие из стоимостей восстановления отказавших элементов C i . При этом элементы с большей стоимостью восстановления должны обладать большими ВБР P i ( t ). То есть при стоимостях восстановления элементов C 1 , C ₂, . ., Cn набору ПР элементов X 1

, X 2

, ..

. , X n должен быть сопоставлен набор обратных величин стоимостей 1/ С 1 , 1/ С ₂, ... , 1/ C n . Указанное

соотношение может быть записано суммами

1 =

' 2

C

⁺ ... ⁺ - П ,

² C

в которых принятые условия для ПР X i получаются из почленного равенства слагаемых:

X ,

C i

X yl.

² C

Правую часть этого равенства назовем «весовой коэффициент стоимости восстановления последовательно взаимодействующих элементов»:

C ai = — .

² C i

Значения ПР X , , отвечающие условию ранжирования:

• X , = Ха , .                                                  (18)

Единица измерения стоимости восстановления не имеет значения, так как в (17) используются отношения стоимостей. Нисходящий анализ ВБР элементов ТС с последовательным взаимодействием рассмотрен в примере 1. Представленная ниже система содержит для простоты три элемента. Однако для действия алгоритма, основанного на (14-18), возможно любое число элементов.

Пример 1. Расчет вероятностей безотказной работы элементов ТС с последовательным взаимодействием (см. рис. 1, а ). Исходные данные:

• —    ВБР системы P ( Г) = 0,9;

• —    число элементов n = 3;

• —    стоимости восстановления элементов (в у. е.): С 1 = 5000, С ₂ = 3000, С ₃ = 2000.

ПР для ВБР ТС (15): X lg P ( T ) = lg 0,9 = -0,04576.

Результаты пооперационного расчета ВБР элементов представлены в табл. 2.

ВБР элементов ТС при их параллельном взаимодействии. Рассмотрим следующую ситуацию: отказ системы при отказе всех элементов с вероятностью F ( T ) в момент времени t = T , соответствующий выбранной наработке. В этом случае основное свойство параллельно взаимодействующих элементов (см. рис. 1, б) согласно (8) выражается через вероятность отказов элементов F j (T ) : m

F ( T ) = П ^F j (^T ).

j = 1

Принимая по аналогии с (14)

F(T) = 10Y,(19)

где Y определяется из логарифмического уравнения lg ( F ( T )) = Ylg 10:

Y = lg F(T).(20)

Показатель степени Y назовем параметром ранжирования вероятности отказа ТС. Если речь идет об элементах системы, показатели степени Y_j называются параметрами ранжирования вероятности отказа элементов. Условия (8, 19) могут быть представлены произведением 10 X = 10 Y ¹ x 10 Y ² x ... x 10 ^Yn , откуда

Y = Y1 + Y2 +... + Yn.(21)

Из множества возможных комбинаций Y j в (21) выбираются вытекающие из стоимостей восстановления отказавших элементов С j . При этом элементы с большей стоимостью восстановления должны обладать меньшими вероятностями отказа (что также означает большие ВБР). То есть при стоимостях восстановления элементов С 1 , С ₂,. .. , C m ряду показателей степени Y , Y , ,..., Y_m должен быть сопоставлен ряд стоимостей С 1 , С ₂,..., C_m . Указанное соотношение может быть записано суммами

YY Y

1 = -¹- +   + ... + - m и 1 =

YY

Y

СС +     ² + ... + ^m .

s Cj   s C

Здесь выбранные условия для показателей степени при Y_j получаются из почленного равенства слагае-

мых:

s C

Правую часть равенства назовем «весовой коэффициент стоимости восстановления при па-

Машиностроение и машиноведение

Таблица 2

Расчет ВБР элементов ТС с последовательным взаимодействием

Объект С , у. е. 1/ С, a, (17) X (18) P(T) (14) ТС -0,04576 0,9 Элемент 1 5000 0,0002 0,193548 -0,00886 0,979814 Элемент 2 3000 0,000333 0,322581 -0,01476 0,966584 Элемент 3 2000 0,0005 0,483871 -0,02214 0,950297 Контрольные суммы и S (1/С) S a- S X P(T) = П P (T) произведения 0,001033 1 -0,04576 0,9 раллельном взаимодействии элементов»:

C bj=хС ■                                    (22)

Значения ПР Y j , отвечающие сформулированному выше соотношению:

Y j = Yb j .                                                     (23)

Нисходящий анализ вероятностей отказов и ВБР элементов ТС с параллельным взаимодействием рассмотрены в примере 2. Система состоит из трех элементов.

Пример 2. Расчет вероятностей отказа и ВБР элементов технической системы с параллельным взаимодействием (см. рис. 1, б) . Исходные данные:

• —    ВБР системы P ( T) = 0,9;

• —    число элементов m = 3;

• —    стоимости восстановления элементов (в у. е.): C 1 = 5000, C ₂ = 3000 и C ₃ = 2000.

Рассчитаем показатели надежности системы. Вероятность отказа системы из (9):

F ( T ) - 1 - P ( T ) = 1 - 0,9 = 0,1.

Значения ПР для вероятности отказа системы из (20):

Y - lg F ( T ) - lg 0,1 = -1.

Результаты пооперационного расчета приводятся в табл. 3.

Расчет ВБР элементов ТС с параллельным взаимодействием

Таблица 3

Объект	C j , у. е.	b j (22)	Y j (23)	F j = 10 Y	P j (T ) = 1 - F j (T )
ТС			-1	0,1	0,9
Элемент 1	5000	0,5	-0,5	0,316228	0,683772
Элемент 2	3000	0,3	-0,3	0,501187	0,498813
Элемент 3	2000	0,2	-0,2	0,630957	0,369043
Контрольные суммы и произведения	2 C j	2 b j	2 Y j	F ( T ) = П F j (T )	P (T ) = 1 - П (1 - P j (T ))
	10000	1	-1	0,1	0,9

Пример 3. Расчет вероятностей безотказной работы элементов комбинированной ТС (см. рис. 1, в ). Исходные данные:

• — число последовательно взаимодействующих подсистем n = 3;

— число параллельно взаимодействующих элементов подсистемы ПС3 m = 4;

— ВБР системы P ( T ) = 0,95;

— стоимости восстановления подсистем (в у. е.): C 1 = 5000, C ₂ = 8000, C ₃ = 12000;

— стоимости восстановления параллельно взаимодействующих элементов (в у. е.): C ₃₁ = 3000, C ₃₂ = 4000, C ₃ , ₃ = 5000, C ₃ , ₄ = 6000.

Рассчитаем параметры надежности системы. ПР для ВБР ТС из (15):

X - lg P ( T ) - lg 0,95 = -0,022276.

Результаты пооперационного расчета приводятся в табл. 4 и 5.

Расчет ВБР подсистем ТС с последовательным взаимодействием

Таблица 4

Объект	C , у. е.	1/ C i	a, (17)	X (18)	P ( T ) (14)
ТС				-0,022276	0,95
ПС 1	5000	0,000200	0,489796	-0,010911	0,975190
ПС 2	8000	0,000125	0,306122	-0,006819	0,984421
ПС 3	12000	0,000083	0,204082	-0,004546	0,989587	◄ *
Контрольные суммы и произведения		2 (1/ C )	2 a ,	2 X	P(T ) = П P ( T )
		0,000408	1	-0,022276	0,95

*

◄ — знак выбора подсистемы для дальнейшего нисходящего анализа.

Из табл. 4 ВБР подсистемы ПС3 P 3 ( T ) = 0,989587. Вероятность отказа ПС3 (8)

F₃(T ) = 1 - P ₃( T ) = 1 - 0,989587 = 0,010413 . ПР для вероятности отказа ПС3 (22):

Y = lg F ₃( T ) = lg 0,010413 = - 1,982407 .

Результаты пооперационного расчета приводятся в табл. 5.

Расчет ВБР элементов ТС3 с параллельным взаимодействием

Таблица 5

Объект	С , у. е.	b j (22)	Y j (23)	F j = 10 Y	P j (T ) = 1 - F j (T )
ПС3			-1,982407	0,010413	0,989587
Элемент 3,1	3000	0,166667	-0,330401	0,467303	0,532697
Элемент 3,2	4000	0,222222	-0,440535	0,362631	0,637369
Элемент 3,3	5000	0,277778	-0,550669	0,281405	0,718595
Элемент 3,4	6000	0,333333	-0,660802	0,218372	0,781628
Контрольные суммы и произведения	Е C j	Е b j	Е Y	F ( T ) = П F j (T )	P ( T ) = 1 - П (1 - PT ))
	18000	1	-1,982407	0,010413	0,989587

Следует принять требуемую наработку ТС и всех ее элементов (1), чтобы ВБР элементов, рассчитанных в табл. 2-5, были исходными данными для расчета и подбора элементов с заданным уровнем надежности.

Необходимо определить полученные ресурсы по соответствующим моделям надежности с расчетными ВБР (табл. 2, 3, 5). Для этого учитываются размеры и конструктивные параметры элементов (деталей, стандартных и других невосстанавливаемых изделий), полученные на стадии эскизного проекта. Затем могут быть приняты меры для сближения полученных и заданных ресурсов [15, 16].

Заключение. Разработан и проверен на численных примерах метод нисходящего анализа структурных схем надежности машин. Его алгоритм совпадает с последовательностью стадий проектирования: от ВБР машины — к ВБР ее деталей. Выбор требуемой наработки и распределение ВБР по деталям на начальных стадиях проекта обеспечивают возможность проектирования с заданным уровнем безотказности. Структурная схема может базироваться на структуре конструкции. Таким образом , обеспечивается универсализация подхода к формированию структурных схем надежности при различных видах взаимодействия элементов. Критерий ранжирования ВБР элементов — стоимость восстановления элемента в случае его отказа. В нее на любом уровне структурной схемы включается денежный эквивалент стоимостей материалов, изделий, ремонтных работ, ущерба от отказа. Они с достаточной точностью известны на начальной стадии разработки машин.

Устранена необходимость использования экспоненциального закона при нормировании надежности и разработке ее структурных схем. Анализ ВБР опирается только на фундаментальные свойства надежности, общие для всех технических объектов и систем. Алгоритм анализа сохраняется на всех уровнях структурных схем, включая уровни деталей.

Машиностроение и машиноведение

Математические модели структурных схем просты, доступны для расчетов на ранних стадиях проекта, одинаково эффективны для последовательно взаимодействующих, резервированных и комбинированных схем надежности. Они дают удобные возможности алгоритмизации, программирования и коррекции данных.