Нагрев и разрушение отложений в нефтепроводах движущимся источником электромагнитного излучения
Автор: Акчурина В.А.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Физика
Статья в выпуске: 1-7 (1), 2016 года.
Бесплатный доступ
Проводятся расчёты процесса нагрева и расплавления пробки из твёрдых отложений в трубопроводе воздействием одного из типов электромагнитных волн, способных распространяться в нем, как в круглом волноводе. Полагается, что источник электромагнитных волн движется. Это позволяет избегать перегрева среды в одних точках и расплавлять твёрдые отложения по всей длине пробки. При воздействии на среду рассмотренным типом волн получаются сложные конфигурации распределения тепловых источников и температуры, особенно в случае движущегося источника электромагнитных волн.
Электромагнитные волны, парафиновые отложения
Короткий адрес: https://sciup.org/170184201
IDR: 170184201
Текст научной статьи Нагрев и разрушение отложений в нефтепроводах движущимся источником электромагнитного излучения
Основная часть природных углеводородов транспортируется в нефте- и газопроводах, особенно от скважин к месту сбора углеводородов. В зимнее время на стенках трубопроводов могут образовываться твёрдые отложения, иногда полностью их закупоривающие. В результате возникает проблема разрушения образовавшейся пробки. Для удаления пробок обычно используют тепловые, химические и механические методы. Все они технически очень сложны, требуют больших финансовых затрат или загрязняют окружающую среду. Требуется разработка метода очистки трубопроводов менее сложного, затратного и экологически безопасного.
Таким методом является воздействие на пробку высокочастотного (ВЧ) или сверхвысокочастотного (СВЧ) электромагнитного (ЭМ) поля. При этом методе воздействия на среду происходит объёмное поглощение энергии ЭМ волн, преобразование её в тепловую энергию, появление распределённых источников тепла. В результате температура среды повышается, если это твёрдое вещество, достигается температура его плавления или разрушения (например, газогидрат или парафино-гидрат). После расплавления или разрушения вещество может быть удалено.
Лучше всего передавать ЭМ энергию посредством ТЕМ-волн, которые могут распространяться в межтрубном пространстве скважины, т.к. у этого типа волн нет ограничений на частоту ЭМ поля. Поэтому расплавление твёрдых отложений в скважине может быть произведено на большую глубину. Иное дело трубопровод, в электродинамическом отношении представляющий собой круглый волновод, в котором могут распространяться только волны типа Е или Н и существуют критические частоты, ниже которой ЭМ волны не могут распространяться. В таком случае, если нефтепровод имеет небольшой радиус, в нём могут распространяться ЭМ волны очень большой частоты, которые быстро затухают. Вследствие этого расплавление образовавшейся пробки может быть только на небольшую глубину. Поэтому в работе [2, 5] предлагается разрушать асфальто-парафиновые отложения в нефтяных трубопроводах с помощью движущегося источника ВЧ ЭМ излучения – «ЭМ крота». При этом методе источник ВЧ ЭМ излучения передвигается по мере перемещения поверхности раздела твёрдой и жидкой фаз, проплавление диэлектрической пробки получается более эффективным. Рассмотрен случай распространения в волноводе волны типа Е01.
Однако не всегда возможно или даже невозможно возбуждение в волноводе желаемого типа волны, особенно если используется движущийся источник ВЧ ЭМ излучения. Обычно в волноводе распространяется сразу несколько типов волн. Поэтому необходимо рассмотрение про- цесса расплавления пробки и другими типами волн. В предлагаемой работе рассматривается процесс разрушения пробки волной типа Н01.
Постановка задачи. Основные уравнения. Так же, как в работе [1-5, 8], полагается, что диэлектрик (парафин) полностью заполняет волновод, решается уравнение теплопроводности. Рассматривается процесс расплавления пробки в нефтепроводе такого же диаметра, что в работе [1, 5]. У волны типа Н 01 цилиндрические составляющие напряженности ЭМ поля Е r =Н φ =0. Остаются компоненты поля:
E, = i М H о J 0( Xr )e "“(z - z°';(1)
X
Hr =- ia H о J ‘(xr >-“(z - z0);(2)
X
Hz = H0 J0 (xr >"^'-'0),(3)
где i – мнимая единица; ω – круговая частота ЭМ поля; ^o - магнитная постоянная (полагается, что среда в волноводе немагнитный диэлектрик); x = —— попе-R речный волновой коэффициент;
а = а + а = 2к" — коэффициент затуха- ния мощности ЭМ волн вдоль волновода, ось которого совпадает с осью цилиндрической системы координат r, φ, z; „ ю 2 s‘ а = —у--- коэффициент затухания,
V c2 к’ обусловленный объёмными потерями в диэлектрической пробке;
to8‘ (У а =----коэффициент затуха- cRk‘ \ 2по ния, обусловленный поверхностными потерями в металлических стенках цилиндрического волновода; с – скорость света; е'о, s’ - действительная и мнимая части комплексной диэлектрической проницаемости парафина s0 = s’ + is’; к‘, к ". - действительная и мнимая части продольного волнового числа к = к' + ik"; о -zz z проводимость металла, из которого сделаны стенки труб; H0 – амплитуда напряженности магнитной составляющей поля; J0, J1 – функции Бесселя нулевого и первого порядка; ' – знак производной; z0 – координата подвижного источника ЭМ волн; в начале ЭМ воздействия источник расположен в точке z=0; м - значение n-го корня функции Бесселя; R – радиус волновода. Для волны типа Н01 - м =3,832.
Как видно из выражений (1) – (3), ЭМ поле имеет единственную составляющую напряженности электрического поля Е φ . Она и определяет распределение тепловых источников, т.к. плотность тепловых источников пропорциональна квадрату напряженности электрической составляющей ЭМ поля. Используя форму написания выражения плотности тепловых источников для неподвижного источника работы [1, 5], получаем:
Н1
О =---S o--- A l р
Q 0 п Re ( к^ о ) R4 P
^z t R 1 J1 („
1 J 1 I Ц п
М п V R
, (4)
где Р – мощность источника ЭМ волн.
В выражении (4) использована формула дифференцирования: J ‘ ( x r ) =- - Jv( x r ) •
Как видно из выражений (1) – (3), задача аксиально-симметричная. Как и в работе [2], задача решается численно методом сквозного счёта без явного выделения фаз. Уравнение теплопроводности имеет вид:
d T 1 d Г d T ) d faT )
PCT — =1 И— 1 + — I Я— 1 + Q(r, z, t ),(5) dt r dr V dr J dz V dz J где ρ, c , λ – плотность, теплоёмкость, теплопроводность высокопарафинистой нефти.
Плотность и теплопроводность нефти считаются не зависящими от температуры, а теплоёмкость при температуре фазового перехода ТS имеет δ-образную особенность cT = c 0 + L5(T - Ts ),
где L – скрытая теплота фазового перехода; 5 ( 7 - T s ) – дельта-функция.
Плотность мощности объёмного тепловыделения записывается в виде [2]:
Q = Q 0 ® ( z - z 0 ( t )) exP (- « ( z - z 0 ( t ))) . (7)
Формула учитывает передвижение источника ЭМ волн по закону z = z0 ( t ) . Явный вид Q 0 приведён в выражении (4). В формуле (7)
виде конвективного теплообмена, но с другим коэффициентом теплообмена κ :
- A ^-I r . r = к ( 7 - 7 0 ) , (10)
dr где к = Nu • AR — коэффициент теплообмена с внешней средой; Nu – число Нуссельта.
В точке r= 0 теплообмен отсутствует:
® ( z - z 0 ) =
f l, k
z ^ z 0
z < z 0
- A ^-|r . „ = 0 . (11)
d r
Значение Р в выражении (4) не отображает действительную поглощаемую мощность ЭМ энергии. Чтобы определить её, методом трапеций определяется объёмный интеграл
HR
Qобщ= 2n J J Q(r, z)rdrdz, вычисляется коэффициент, показывающий насколько действительная поглощаемая мощность отличается от задаваемой мощности, затем выражение (4) умножается на этот коэффициент. В интеграле Н – длина парафиновой пробки.
Для решения уравнения (5) принимались граничные условия. На торце пробки z =0 задавался конвективный теплообмен по закону Ньютона [4,5]:
A ^-I z . 0 = к , ( 7 - 7 0 ) , (8)
dz где Т0 – температура окружающей среды и начальная парафиновой пробки; к — коэффициент теплообмена.
На удалённом торце пробки z = Н теплообмен отсутствует:
A ~ z . H = 0. (9)
d z
На боковой поверхности цилиндра r=R граничное условие также записывалось в
Скорость движения источника ЭМ волн v вдоль координаты z задавалась постоянной и подбиралась так, чтобы за источником не оставалось зон с нерасплавленным парафином (в расчётах использовалось значение v = 1,44 м/час).
Анализ результатов вычислений. При проведении расчётных исследований использовались параметры высокопарафинистой нефти [1]: ρ =950 кг/м3; c =3 кДж/(кг·К); λ =0,125 Вт/(м·К); L =300 кДж/кг; κ =1,613 Вт/(м2·К); Nu =1 (труба в сухом грунте); κ 1 =0,2 Вт/(м2·К); T 0 =20 0C; T S =50 0C; H =5 м; Р =9,34 кВт; R =0,0775 м; £ ‘ =2,3; tg5= s’/^‘ =0,012; п =3Л10 6 Ом-1·м-1. Задача решалась неявным методом переменных направлений с равномерной прямоугольной сеткой. Дельта-функция в выражении для теплопроводности аппроксимировалась ступенькой с полушириной равной 0,6 0С.
На рис. 1 приведена зависимость мнимой части продольного волнового числа k‘ от частоты ЭМ поля. Критическая частота Н01 волны для рассматриваемого цилиндрического волновода f0≈1,556·109 Гц. Мнимая часть продольного волнового числа имеет минимум k" -0,5967 м-1 на частоте f0≈2,2·109 Гц. На рис. 2 приведены распределения Q(r, z=0), нормированные на мощность источника ЭМ волн, в поперечном сечении волновода для различных частот при неподвижном источнике. Как видно из рис. 2, распределение тепловых источников в поперечном сечении волно- вода очень неравномерно и неравномерность увеличивается с ростом частоты. Максимум плотности тепловых источников находится приблизительно в середине между осью и стенкой волновода. В про- дольном направлении плотность тепловых источников падает по экспоненциальному закону. С ростом частоты скорость спадания тепловых источников в продольном направлении увеличивается.
Imk z
1.4
1.2
1.0
0.8
0.6

*.4^ 1 । 1 I i 1 i 1 i f ггц
Рис. 1. Мнимая часть продольного волнового числа, как функция частоты для ме-
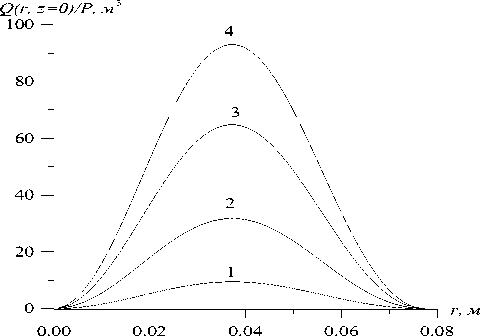
Рис. 2. Поперечное распределение плотности мощности тепловых потерь, нормированной на мощность источника в цилиндрическом волноводе, заполненном парафином f , 109 Гц; 1 – 1,6; 2 – 2; 3 – 3; 4 – 4.
таллического цилиндрического волновода, заполненного парафином.
Наиболее эффективно удаление пробки ЭМ полем с частотой f =2·109 Гц. В этом случае наблюдается наименьший перегрев парафина в точках максимума температуры, который приходится допускать ради расплавления парафина возле стенки трубопровода. На этой частоте раньше можно начинать движение источника ЭМ волн (через 5 минут после начала нагрева), т.к. через это время уже происходит процесс проплавления парафина возле стенки волновода. При других рассмотренных частотах движение источника ЭМ волн приходится начинать позже – через 70 минут после начала нагрева. Иначе возле стенки волновода парафин остаётся не расплавленным. Но к этому времени уже наблюдается сильный перегрев парафина в некоторых точках. Раз позже приходится начинать движение источника ЭМ волн, то дольше приходится и греть парафин ради расплавления его по всей длине пробки.
Заключение. Рассмотрен процесс удаления парафиновой пробки одним из воз- можных типов волн, которые могут быть возбуждены в круглом волноводе – Н01. Расчёты показали, что чем меньше частота возбуждаемых ЭМ волн, тем эффективнее разрушение пробки. С ростом частоты ЭМ поля эффективность удаления пробки уменьшается, а неравномерность температуры среды в поперечном сечении волновода увеличивается. Это происходит потому, что с ростом частоты наблюдается уменьшение глубины проникновения ЭМ поля в среду. Поверхность, разделяющая твёрдую и жидкую фазы, имеет форму конуса с радиусом, уменьшающимся вдоль пробки. Такая форма расплавленной зоны может привести к разрушению пробки до её полного расплавления. Если преследовать цель пробить в пробке отверстие по всей её длине, а не расплавлять её по всему радиусу трубопровода, то движение «ЭМ крота» можно начинать намного раньше и двигать быстрее. В таком случае более высокие частоты могут иметь даже преимущество.
Список литературы Нагрев и разрушение отложений в нефтепроводах движущимся источником электромагнитного излучения
- Акчурина В.А. Электромагнитное воздействие на углеводородные отложения // Современные тенденции развития науки и технологий. - 2016. - №6-1. - С. 7-12.
- Акчурина В.А., Фатыхов М.А. Математическое моделирование расплавления диэлектрической пробки, заполняющей трубу, движущимся источником электромагнитного излучения // Академический журнал Западной Сибири. - 2014. - Т.10. - №2. - С. 31.
- Абдуллина В.А., Фатыхов М.А. Расплавление твердых отложений в трубопроводах движущимся источником электромагнитного поля // Электронный научный журнал Нефтегазовое дело. - 2012. - №6. - С. 60-68.
- Абдуллина В.А., Фатыхов М.А. Особенности изменения источников тепла в круглом волноводе заполненном многофазной средой // В мире научных открытий. - 2010. - №4-10. - С. 145-147.
- Балакирев В.А., Сотников Г.В., Ткач Ю.В., Яценко Т.Ю. Разрушение асфальто-парафиновых отложений в нефтяных трубопроводах движущимся источником высокочастотного электромагнитного излучения // Журнал технической физики. - 2001. - Т. 71. выпуск 9. - С. 1.
- Кислицын А.А. Численное моделирование высокочастотного электромагнитного прогрева диэлектрической пробки, заполняющей трубу // Журнал прикладной механики и технической физики. - 1996. - Т.37. - №3. - С. 75-82.
- Лебедев И.В. Техника и технология СВЧ. - М.: Высшая школа, 1970. - 440 с.
- Фатыхов М.А., Абдуллина В.А. Электромагнитный способ плавления парафина в трубе // Автоматизация, телемеханизация и связь в нефтяной промышленности. - 2012. - №7. - С. 25-28.


