Нахождение движущихся видеообъектов с применением локальных 3D-структурных тензоров

Задача нахождения объектов из видеопоследовательностей с целью их дальнейшего распознавания и предсказания поведения востребована во многих приложений цифрового видео, таких как мультимедиа, виртуальная реальность, компьютерное зрение, искусственный интеллект. Существуют различные методы нахождения видеообъектов, которые объединяют сегментацию изображения (пространственные методы) и сегментацию на основе признаков движения (временные методы) с целью повышения точности нахождения этих объектов. Обычно подходы к сегментации видеообъектов классифицируются по трем категориям: методы, основанные на поиске регионов, методы, основанные на определении границ, и вероятностные методы [1–3].

Методы, основанные на поиске регионов, используют информацию о кластеризации или операциях расщепления и выращивания регионов в пространстве признаков. Такая информация обычно формируется из векторов движения и некоторых пространственных признаков: цветности, текстуры, взаимного расположения. Недостатками такого подхода являются проблемы появления, перекрытия и исчезновения регионов из кадра, а также низкая точность определения границ регионов.

Методы определения границ обычно используют угловые детекторы или активные контуры в сочетании с информацией о полях движения видеообъектов. Такие методы основаны на принципах когнитивной психологии, однако они имеют низкую помехоустойчивость, а активные контуры – еще и сильную зависимость от выбора начальных параметров.

Вероятностные методы для нахождения движущихся объектов используют байесовский подход, алгоритм максимизации-ожидания, минимизации расстояний в различных метрических пространствах.

Указанные подходы обладают высокой вычислительной сложностью, причем некоторые методы требуют предварительного задания количества объектов-регионов в качестве входного параметра, что ограничивает их использование на практике.

Примем, что рассматривается сложная сцена с движением нескольких объектов. Объекты могут двигаться с различной скоростью, ускорением, в разных направлениях и иметь различные локальные размеры. Изображение объекта Oi может включать набор регионов {Rj}, обладающих разделимыми цветовыми ColorParams(Rj) и текстурными TextureParams(Rj) показателями. Интерпрета- ция регионов как единого объекта производится на основе анализа показателей движения MotionParams(Rj) и повторяемости поведения регионов (в простейшем случае это отслеживание траектории перемещений регионов). Поскольку методы определения цветовых и текстурных показателей достаточно хорошо изучены, остановимся на нахождении показателей движения.

Известны два основных метода оценки движения, используемых для временной сегментации: метод оптического потока и метод соответствия блоков. В обоих подходах информация о движении формируется путем обнаружения изменения интенсивности пикселей между последовательными кадрами. При этом метод оптического потока обеспечивает более точное нахождение границ регионов, так как он использует информацию на уровне пикселей и лучше выделяет регионы со сложной текстурой, имеющие большие значения градиентов.

Видеопоследовательность I ( x ), представленную в виде набора кадров, где x = [ x , y , t ] ^T , здесь x и y – пространственные координаты пикселей кадра по осям OX и OY соответственно, t – временная координата, учитывающая последовательность появления кадров, можно интерпретировать как трехмерный объем данных. Известно, что 3D - структурный тензор J позволяет эффективно определять локальную ориентацию пространственно-временного движения видеообъектов и определяется следующим образом:

^J 11

^J 21

^J 31

Jx) =

^J 12 ^J 13

^J 22 ^J 23

^J 32 ^J 33

I x ²   I x I y    I x I t

I y I x    I y ²    I y I t

I t I x    I t I y    I t ²

= VI (x )-VI (x) T, где С – пространственно-временной градиент, вычисляемый по частным производным

Собственные векторы ek (k = 1, 2, 3) симметричной ковариационной матрицы Jразмером 3x3 можно определить по локальным смещениям интенсивностей изображений соседних кадров и использовать для оценки ло- кальных ориентаций движущихся сегментов. При этом, в силу особенностей видеонаблюдения, собственные значения Xk векторов ek указывают на локальные отклонения яркости по трем направлениям и могут быть отсортированы в следующем порядке: X1 > X2> X3> 0. Выражение VI(x) ■ VI(x) T можно рассматривать как корреляционную матрицу, составленную из векторов градиентов в пространственно-временном объеме. В соответствии с методом главных компонент собственные векторы корреляционной матрицы сортируются в порядке убывания. Первый собственный вектор, соответствующий наибольшему собственному значению, указывает направление наибольшего изменения данных. Отношение каждого собственного значения к сумме трех собственных значений характеризует концентрацию энергии по соответствующему направлению. Таким образом, собственные значения собственных векторов локального 3D - структурного тензора можно использовать для обнаружения локальных изменений в последовательности кадров. Наименьшее собственное значение можно использовать для определения различий в кадрах, оно является более устойчивым к шуму и низко контрастным объектам фона по сравнению с простейшим методом яркостной разницы кадров.

На основе собственных значений X ₁( x , y , t ), X ₂( x , y , t ), X ₃( x , y , t ) можно построить карты X 1 ( I ), X ₂( I ), X ₃( I ) локального 3D - структурного тензора. При этом карта собственных значений X 1 ( I) фиксирует как движущиеся объекты, так и некоторые изолированные текстурные регионы фона, карта X ₂( I) является менее информативной для сегментации, а карта X ₃( I) генерирует небольшие разрывы внутри масок видеообъектов. Поэтому при обнаружении движения основное внимание следует уделять первому собственному вектору корреляционной матрицы X 1 ( I).

Рассмотрим процесс нахождения объектов из видеопоследовательностей, который представляет собой слож ную совокупность действий, особенно если сцена имеет несколько разнонаправленных движущихся объектов, а начальные условия наблюдения отсутствуют. Целесообразно принять, что имеются три этапа получения, обработки пространственно-временной информации и принятия решения:

• -    первый этап - предварительный анализ сцены (пред-сегментация);

• -    второй этап - пространственно-временная сегментация сцены;

• -    третий этап - постсегментация (с учетом многоуровневого движения) и распознавание объектов интереса сцены.

Этап предсегментации предназначен для грубой оценки пространственно-временных характеристик сцены (рис. 1). Предлагается использовать не исходное изображение опорного кадра Fr ₀, а преобразованный с помощью гауссовой пирамиды слой с малым разрешением, что позволяет снизить количество обрабатываемых пикселей в 2 K раз, где K - номер слоя пирамиды Гаусса, без значительной потери качества. Гауссова пирамида строится как для опорного кадра Fr ₀, так и для последовательности кадров Fr 1 , Fr ₂, _, Fr . Полученные таким образом изображения низкого разрешения обрабатываются для получения информации о предварительной пространственной сегментации сцены (вычисление признаков цветности, интенсивности, текстурных характеристик регионов и формирование гомогенных регионов) и предварительной временной сегментации (использование локальных 3D - структурных тензоров и вычисление коэффициентов корреляции между соседними кадрами).

Для грубого нахождения движущихся регионов целесообразно вычислять коэффициент R корреляции между кадрами, используя наименьшие собственные значения X ₃( I t ) и X ₃( I t ₊ 1 ) кадров Fr t и Fr ₊ 1 соответственно:

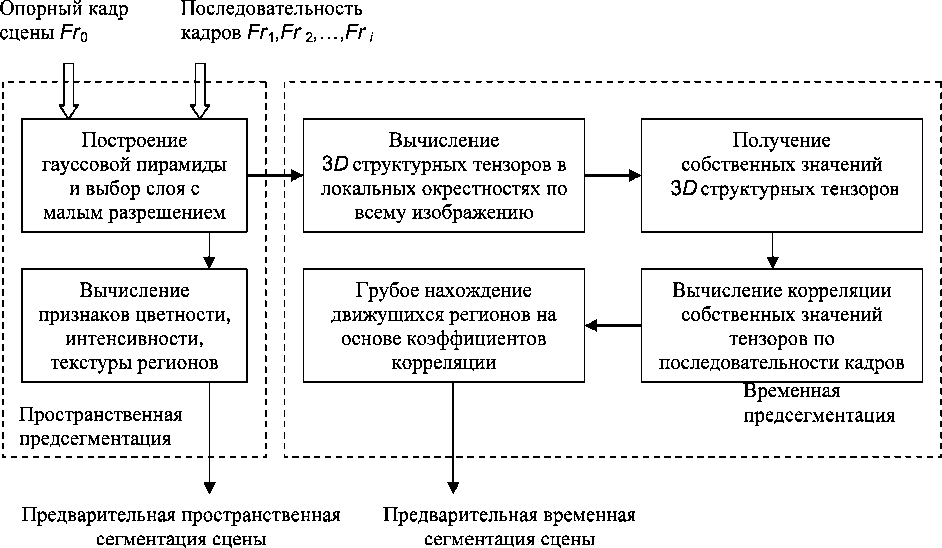
Рис. 1. Этап предварительного анализа сцены (предсегментация)

R =

NNN

Z ( Vi- MY Vi- Y U i i =1                     \ i =1         i =1

( N.

Y v2

I i =1

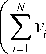
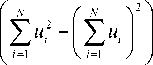
где v. e X3(It) и u. e X3(It + 1); N- общее количество пикселей в кадре.

Разброс коэффициентов корреляции кадров сцены позволяет оценить степень изменчивости формы движущихся объектов. Так, для мало изменяемых по форме объектов он будет значительно меньше, чем для объек тов, характеризующихся значительными изменениями их положений в пространстве. Величину такого разброса можно вычислить, используя стандартную формулу среднеквадратического отклонения:

n

S=Y (R-Rt где n - количество кадров в сцене; R - среднее значение величин R.. Если значение величины S превышает установленное пороговое значение, то считается, что видеообъект претерпевает значительные геометрические изменения. В этом случае процедура сегментации усложняется.

На этапе пространственно-временной сегментации сцены (рис. 2) анализируется полное изображение с уче-

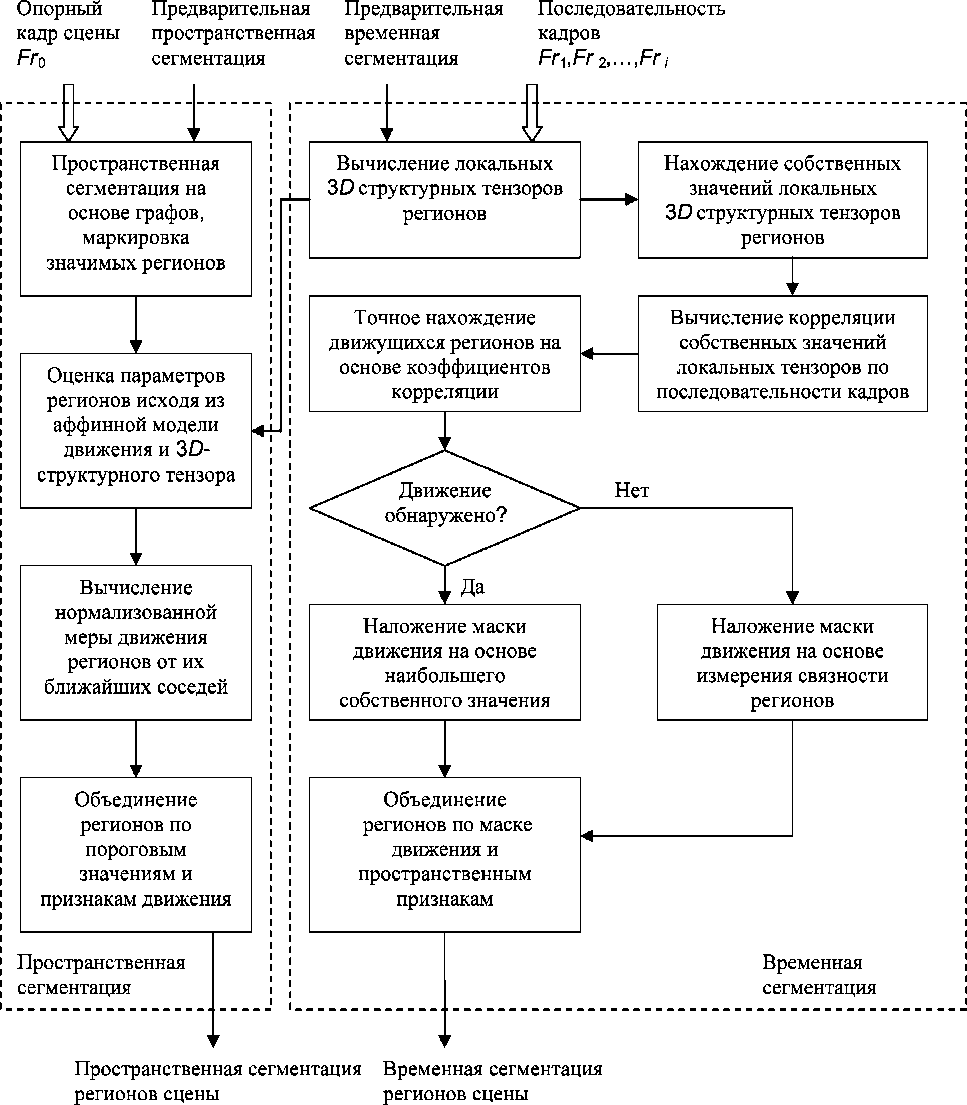
Рис. 2. Этап пространственно-временной сегментации сцены

том информации о регионах, полученной на этапе пред-сегментации. Можно предложить несколько стратегий сегментации в зависимости от дальнейших целей распознавания. Если обработка и распознавание должны происходить в реальном режиме времени и, например, поставлена цель слежения за движущимися объектами, то схему, приведенную на рис. 2, целесообразно применять не ко всем регионам, выявленным на этапе предсегмен-тации, а только к тем, у которых имеются признаки движения. Если поставлена цель распознавания сцены с неизвестным заранее сюжетом, то следует воспользоваться принципами человеческого визуального восприятия: анализом больших по размерам статистически однородных регионов и движущихся регионов с последующим анализом более мелких деталей изображения. Если же происходит поиск какого-либо неподвижного объекта в видеобиблиотеках, то основное значение приобретает пространственная сегментация. Остановимся более подробно на анализе движения регионов.

Для классификации полей движения недеформируе-мых по геометрическим параметрам и деформируемых регионов можно ввести меры сглаженности, вычисляемые с помощью трех собственных значений X k ( I) регионов. Если все три собственных значения равны нулю (ранг матрицы rang( J ) = 0), то перемещения по трем осям ( x , y , t ) отсутствуют, т е. регион неподвижен. Если X 1 ( I) > 0 и X 2 (I) = X 3 ( I) = 0, то rang( J ) = 1 , что говорит о наличии изменений интенсивностей в нормальном направлении, т. е. о движении линии. Если X 1 ( I) > 0, X 2 (I) > 0 и X ₃( I) = 0, то rang( J ) = 2 и наблюдается движение с постоянной скоростью в двух направлениях пространственно-временной структуры, т. е. движение точки. В этом случае оценить параметры движения возможно. Если же все три собственных значения больше нуля, то rang( J ) = 3. Это означает, что локальная зона находится на границе двух полей движения и оценить параметры движения невозможно.

Однако показатель ранга матрицы J нельзя напрямую применить для оценки различных типов движения, поскольку он не является нормализованной мерой для оценки поступательного, вращательного или возвратно-поступательного движения. Следует использовать понятие «мера сглаженности», на основе которого и строят ся маски обнаружения движения.

Собственные значения 3D - структурных тензоров можно использовать для нахождения локальных движущихся структур, таких как границы, углы, статистически однородные регионы и т. д. В работе [4] предложены следующие выражения для определения меры сглаженности недеформируемого региона:

C_t = ((l₁( I ) – l₃( I ))/(l₁( I ) + l₃( I ))) ² , границ деформируемого региона

C_s = ((l₁( I ) – l₂( I ))/(l₁( I ) + l₂( I ))) ² , угловых точек деформируемого региона

CC = Ct - Cs =

_ 4 X 1 ( I ) ( X 2 ( I ) - ^ 3 ( I ) ) ( ( X ( I ) ) 2 - ^ 2 ( I )^ 3 ( I ) )

=          ( X 1 ( I) + Х з ( I ) ) 2 ( X 1 ( I) + X 2 ( I) ) 2         .

Как правило, в реальной сцене найденные объекты группируются по уровням движения. В общем случае необходимо отнести объект к тому или иному уровню движения в зависимости от локальных размеров регионов объекта, значений модулей скорости и ускорения и гипотез, хранящихся в базе знаний.

Обычно в сцене имеется несколько движущихся объектов. Если для сегментации регионов достаточно ввести одно пороговое значение, то к классификации многоуровневого движения следует отнестись более тщательно, учитывая не только модули значений скорости и ускорений, но и направления движений, тем самым группируя регионы по уровням движений (рис. 3). Простейшим способом является метод попиксельного вычитания кадров D(N) с применением лапласиана и сравнением с заранее выбранными пороговыми значениями. При этом возможные ошибки не влияют на окончательную сегментацию, поскольку этот метод используется только для выбора масок движения.

Маски движения необходимы для устранения небольших перемещений объектов фона. Они определяются как процентное соотношение площадей движущихся регио- нов по методу вычитания кадров Mfr с использованием собственных значений локальных 3D-структурных тензо- ров для недеформируемых Meigen и деформируемых

M corner

регионов соответственно:

R c =

^{M fr} 100%, ^M eigen

R = Mf^i—100%. c corner

Как показали эксперименты, после применения масок движения границы движущихся объектов остаются нечеткими, а внутри изображений видеообъектов имеются разрывы. Устранить эти недостатки можно с привлечением результатов пространственной сегментации. Каждый пространственный регион маркируется, и находится процентное отношение площадей движущихся регионов M _move и пространственных регионов M _seg:

R = M m™ 100 o_/o.

m seg

Если значение R_m превышает заранее установленное пороговое значение (например, 50 %), то весь пространственный регион M _seg считается движущимся регионом. Однако сложные видеообъекты, как правило, состоят из нескольких движущихся регионов. В условиях отсутствия априорной информации формирование видеообъекта можно осуществлять только с использованием характеристик движения соседних регионов.

Известны два подхода к объединению регионов: непараметрический и параметрический. Непараметрический подход, основанный на слиянии границ, нельзя использовать совместно с полями движения, так как для неоднородных полей движения трудно определить точные границы. Более целесообразен параметрический подход, основанный на объединении регионов по функции минимизации энергии или по моделям движения в плоских проекциях аффинной или проективной групп. Задача ставится таким образом, чтобы, используя характеристики локальных 3D - структурных тензоров и параметров аффинной модели движения, можно было бы оценить расстояние между двумя соседними регионами.

Два региона объединяются, если вычисленное расстояние является достаточно малым, чтобы воспринимать объединенный регион как единый объект. Аффинная модель движения содержит шесть параметров:

vx (x, y) = ax + by + c, vy (x, У) = dx + ey + f, где vx и vy - проекции скорости v на оси OX и OY соответственно; a, b, c, d, e, f - параметры аффинной модели.

Тогда проективная модель описывается восемью параметрами:

vx (x, y) = a 1 + a 2x + a 3y + a 7x2 + a 8xy, vy (x, y) = a 4 + a 5 x + a ey + ax + a 8y2.

Для дальнейших рассуждений будем пользоваться более простой аффинной моделью движения. Вектор скорости на плоскости расширим до 3D - направленного вектора v с учетом временной составляющей [4]:

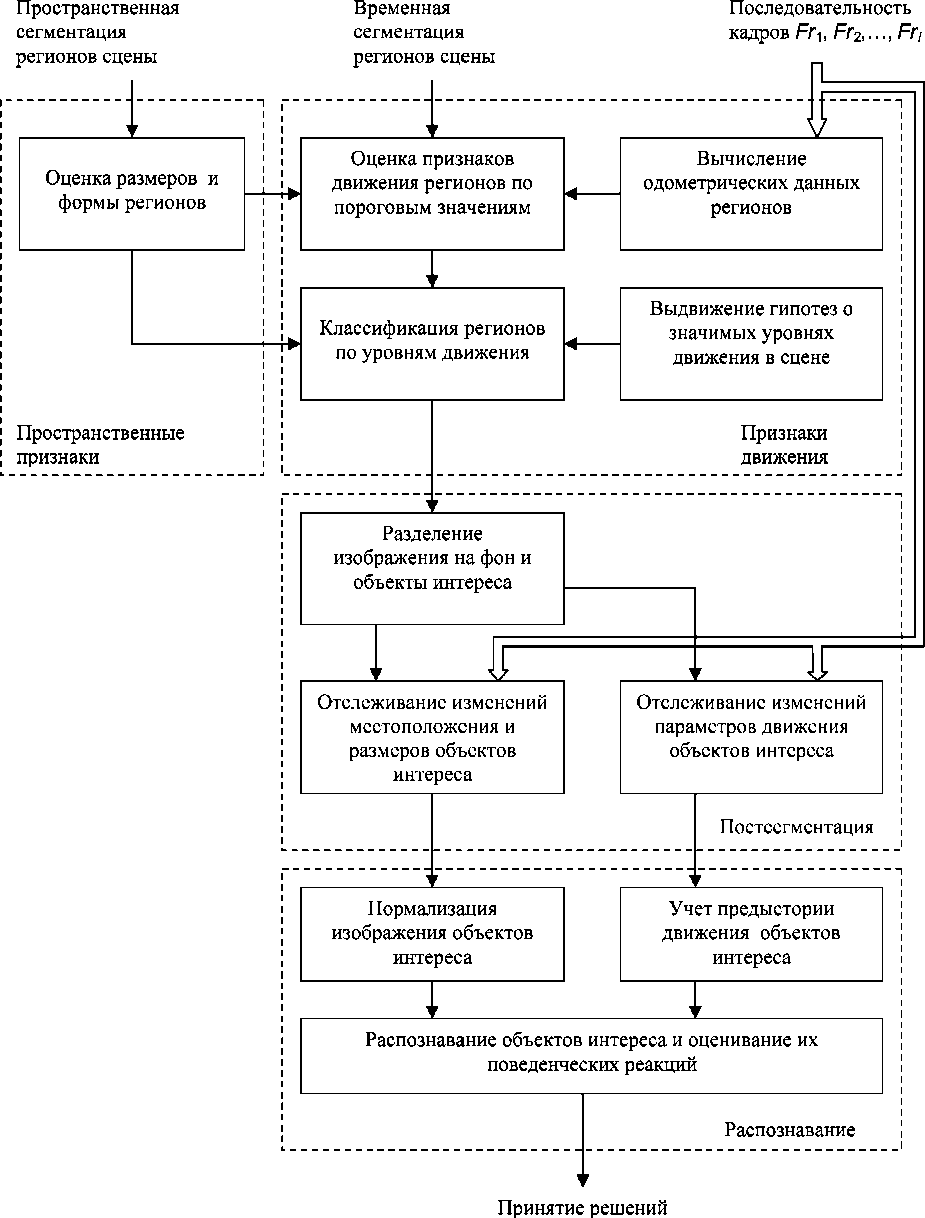
Рис. 3. Этап постсегментации (с учетом многоуровневого движения) и распознавания объектов интереса сцены

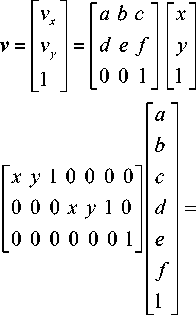
Для объединения регионов используем функции расстояний трех видов:

d 1 (vi, Ji) = vT Jivi, d 2 (Vi, Ji) =

d i ( V , J ) v i ²

d з ( V i , J i ) =

d i ( V i , J ) I V I" tr ⁽ J i )

Выразим расстояние d ₁( v _i , J _i ) следующим образом: d ₁( v _i , J _i ) = v _i ^T J _i v _i = p ^T S _i ^T J _i S _i p = p ^T Q _i p , где Q _i = S _i ^T J _i S _i – положительно определенная матрица. Сумма расстояний внутри заданного пространственного сегмента, содержащего N пикселей, определяется как

"                 Г N   A

d seg (P) = S d 1 (vi’ Ji) = P I S Qi Iх i =1                          \ i=1 /

^X P = P T Q seg P ■

Поскольку величина Q _i при расчете расстояния d ₁( v _i , J _i ) более критична к большим скоростям, чем к малым, то можно использовать нормированное расстояние d ₃( v _i , J _i ).

После проведения процесса постсегментации в течение нескольких последовательных кадров видеопоследовательности можно приступать к нормализации изображения объекта (приведению к эталонному виду) и формированию гипотез о поведении объекта с целью его распознавания с использованием стандартных методов кластеризации.

Таким образом, в данной статье кратко рассмотрены существующие подходы к сегментации видеообъектов, которые классифицируются по трем категориям: методы, основанные на поиске регионов, методы, основанные на определении границ, и вероятностные методы. Показано, что при сегментации сложной сцены с многоуровневыми полями движения регионов целесообразен пространственно-временной подход с применением локальных 3D - струк-турных тензоров. Введено понятие меры сглаженности для деформируемых регионов, для границ и угловых точек недеформируемых регионов на основе собственных значений 3D-тензора. Построены подробные структурные схемы этапов предсегментации, пространственно-временной сегментации и постсегментации сложных сцен, характеризующихся аффинной моделью движения. Введены три функции расстояний на базе локальных структурных тензоров с целью объединения регионов в видеообъект и разделения видеообъектов сцены по уровням движения.