Нахождение оптимального портфеля ценных бумаг из набора активов

Автор: Гук К.О., Мыльцина О.А.

Журнал: Труды Московского физико-технического института @trudy-mipt

Статья в выпуске: 3 (55) т.14, 2022 года.

Бесплатный доступ

В работе производится построение средствами языков R и Python портфелей с наилучшими показателями. Исследуются портфели, содержащие четыре актива. Сравнивается доходность, риск портфелей и коэффициент Шарпа. Изучено поведение портфелей с фиксированными весами и разными активами, а также фиксированными активами и разными весами. Решена задача более быстрого нахождения наилучших весов и активов.

Оптимальный портфель, набор активов, коэффициент шарпа

Короткий адрес: https://sciup.org/142236474

IDR: 142236474

Текст научной статьи Нахождение оптимального портфеля ценных бумаг из набора активов

Под портфелем будем понимать набор ценных бумаг, обращающихся на финансовом рынке. Задача, выбора, оптимального портфеля заключается в выборе такого инвестиционного портфеля, который удовлетворяет требованиям инвестора. Рассмотрим портфели ценных бумаг, содержащие несколько активов с положительными весами. Средним ожидаемым доходом для портфеля с определенными весами и набором активов будем считать математическое ожидание случайной величины дохода R, а риском называют среднее квадратическое отклонение случайной величины R [1-2]. Наилучший портфель будем находить из условия наибольшего коэффициента Шарпа S, который вычисляется как отношение средней премии за риск к среднему отклонению портфеля:

_s = Е \R - Rj ]

а '

где R j - доходность от альтернативного вложения.

2. Портфели с фиксированными активами и портфели с фиксированными весами

При построении портфелей ценных бумаг возможны две ситуации. Можно зафиксировать набор активов и найти наилучшее веса, либо выбрать наилучшее подмножество из множества, активов при фиксированных весах. Данные ситуации были смоделированы на. языке программирования R и результаты представлены на рис. 1 и 2.

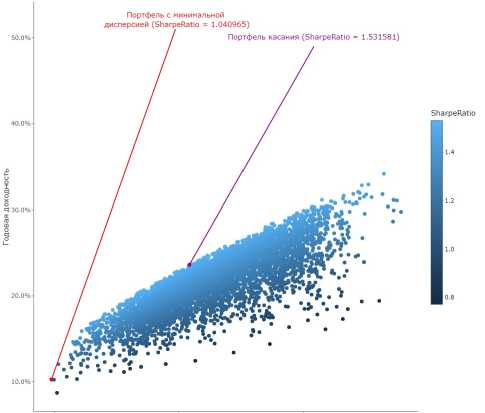
Рис. 1. Портфели с фиксированными активами

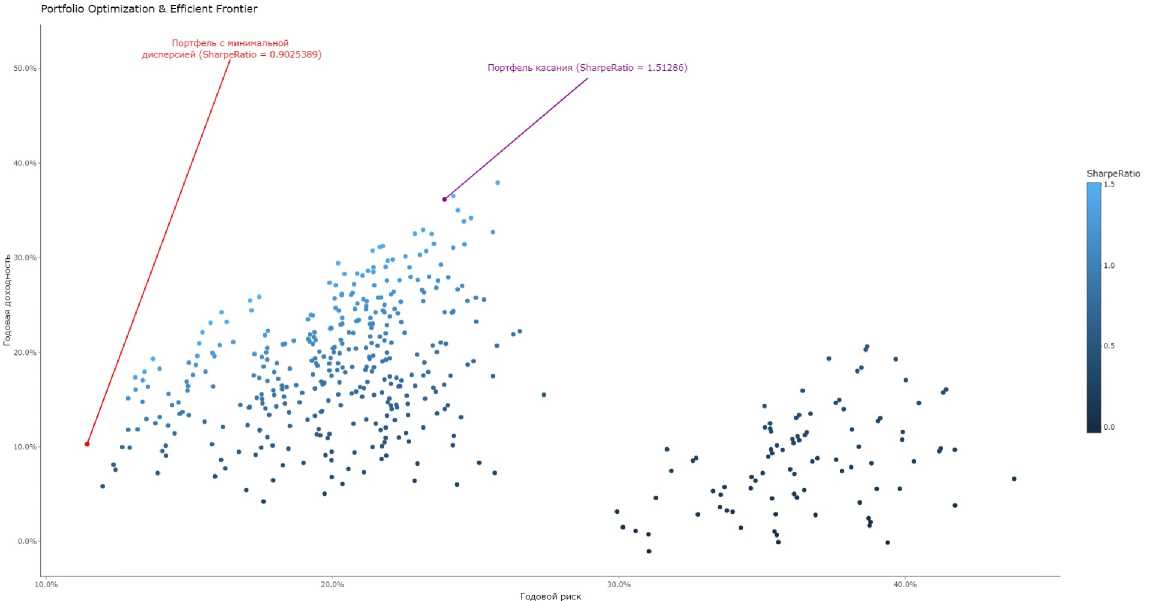
Рис. 2. Портфели с фиксированными весами

На рис. 1 показано распределение активов АМТ, AMZN, DIS, SNE с различными весами. Распределение троек активов с равными долями из списка ВАС, GOLD, PPLT, PDCE, DIS, AMZN, AAPL, MSFT, TGT, JNJ, WELL, TLT, WMT, SNE приведено на рис. 2.

На рис. 3 приведена часть программного кода на языке Python с функцией для подсчета портфелей с фиксированным набором активов, результаты работы которой приведены на рис. 1. Эта функция по заданным активам и временным промежуткам находит 10 000 наборов случайных весов и производит их нормировку. Для каждого из наборов вычислены риск, доходность и коэффициент Шарпа.

На рис. 4 приведена выдержка из программного кода на языке Python с функцией для подсчета портфелей с фиксированным набором весов, результаты работы которой приведены на рис. 2. Целью работы данной функции является нахождение портфеля с наибольшим коэффициентом Шарпа.

def FixingASetOfAssets(tick,start,end):

price_data = yf.download(tick, start, end)['Adj Close1] log ret = np.log(price_data/price_data.shift(l)) cov_mat = log_ret.cov() * 252 print("\n"+"Covariance matrix:") print(cov_mat,'\n') num_port = 10009 all_wts = np.zeros((num_port, len(price_data.columns))) port_returns = np.zeros((num_port)) port_risk = np.zeros((num_port)) sharpe_ratio = np.zeros^(mum_port)|)| for i in range(num_port):

port_ret = (port_ret + 1) ** 252 - 1 port_returns[i] = port_ret port_sd = np.sqrt(np.dot(wts.T, np.dot(cov_mat, wts))) port_risk[i] = port_sd sr = port_ret / port_sd sharpe_ratio[i] = sr names = price_data.columns max_sr = all_wts[sharpe_ratio.argmax()] print("Tangency Portfolio weights") print(max_sr,' \n1 ) print("Max Sharpe Ratio") print(sharpe_ratio.max()) max_sr = pd.Series(max_sr, index=names) max_sr = max_sr.sort_values() dl=pd.DataFrame(max_sr).T tick=" ".join(list(dl.columns)) wts=dl.iloc[0,:].apply(str).values return tick,wts,port_risk[sharpe_ratio.argmax()],port_returns[sharpe_ratio.argmax()],sharpe_ratio.max()

Рис. 3. Нахождение портфеля с наибольшим коэффициентом Шарпа при фиксированных активах def FixingWeights(Tick,wts,start,end):

SetTicks=PermTicks(Tick)

num_port = len(SetTicks)

tick=tick.replace("'", '’).replace('[','’).replace(1]’,'')

print("\n"+"Covariance matrix:”)

print(cov_mat,1\n')

num_port = len(SetTicks)

port_ret = (port_ret + 1) ** 252 - 1

port_returns[i] = port_ret print("Port Returns:",port_returns[i])

names = price_data.columns

DataPr2=pd.coneat([pd.DataFname(SetTicks),pd.DataFrame(all_wts),pd.DataFrame(port_returns),pd.DataFrame(port_risk),pd.DataFname(sharpe_ratio)],sort=Faise,axis=l) DataPr2 = DataPr2.set_axis([ 'Name_l','Name_2','Name_3','Name_4', 'Wts_l','Wtsl 2','Wts_3‘,'Wts_4','Port Returns',1 Port Risk','Sharpe_ratio'], axis=l, inplace=False) DataPr2=DataPr2.sort_values(by=[’Sharpe_ratio1], ascending=False)

return DataPr2

Рис. 4. Нахождение портфеля с наибольшим коэффициентом Шарпа при фиксированных весах

3. Портфель при выборе активов и весов

Произведем изменение в программе для нахождения активов и их весов с наибольшим коэффициентом Шарпа. Но возникает проблема долгого подсчета наилучших весов для каждой комбинации из Ду. Было решено проверить, даст ли схожий результат поочередное выполнение функций выбора активов с определенными фиксированными весами и последующее использование этих активов для нахождения их наилучших весов с результатами одновременного перебора активов и подсчета весов. Все вычисления проводились на языке Python на наборе ВАС, MSFT, PDCE, DIS, AAPL, WELL, для портфеля было выбрано четыре актива, данные были собраны за четыре года. При простом переборе получили таблицу, изображенную на рис. 5, состоящую из С4 = 15 наилучших портфелей по отношению к коэффициенту Шарпа. При осуществлении прямого перебора программа выполняет 150 000 операций.

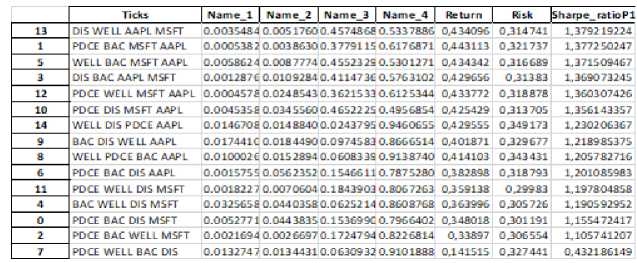
Рис. 5. Простой перебор активов

13 DISWCLL AAPL MSFT 0.003М84 0.0051760 0.4 5748« 0.533 7886 0,434096 0,314741 1,379219224

1	PDCE ВАС MS FT AAPL	O.OOO538 2 0.0038630 0.3779115 0.6176871	0,443113	0 Д21737	1.3772 50247
S	WELL ВАС MSFT AAPL	0.0058624 0.00877740.4552328 0.5301271	0Д 34342	0316689	1.371509467
3	DIS ВАС AAPL MSFT	0.001287C 0.0109284 0.4114736 0.5763102	0Д 29656	031383	1,3690 73245
12	PDCE WELL MSFT AAPL	0.000457 8 0.0248543 0.3 6215 33 0.612 5344	0.4 33772	0318878	1.360307426
10	PDCE DIS MSFT AAPL	0.0045358 0.034556O0.4652225 0.4956854	0,4 2 5429	0313705	1,356143357
14	WELL DIS PDCE AAPL	0.0146708 0.014 8840 0.0243795 0.9460655	0,4 29555	0349173	1,230206367
9	ВАС DIS WELL AAPL	0.017441C 0.01844900.0974583 0.8666514	0Д01871	0329677	1,218985375
8	WELL PDCE ВАС AAPL	0.010002 C 0.0152894 0.0608338 0.9138740	0,414103	0343 431	1,205782716
6	PDCE ВАС DIS AAPL	0.001575 5 0.056 2352 0.15466110.787 5280	0,382898	0318793	1.201085983
	PDCE WELL DIS MSFT	0.001822 7 0.007 0604 0.1843903 0.806 7263	0.359138	039983	1,197804858
4	ВАС WELL DIS MSFT	0.0325658 0.04403580.0625214 0.8608768	03 63996	0305 726	1,190592952
О	PDCE ВАС DIS MSFT	0.0052771 0.044 3835 0.153699C 0.7966402	0,348018	0301191	1.1554 72417
	PDCE ВАС WELL MSFT	0.0021694 0.0026697 0.1724794 0.8226814	0.33897	0306 554	1.105741207
7	PDCE WELL ВАС DIS	0.013274 7 0.01344310.06309 32 0.9101888	0,141515	0 327 441	0,432186149

Далее зафиксировали несколько наборов весов и нашли наилучший набор активов из А4 комбинации. В этом случае программа выполняет 480 операций. Веса (0.001; 0.004; 0.005; 0.99) дадут результаты в виде таблицы на рис. 6. Запуская программу для нахождения весов с набором активов WELL, DIS, MSFT, APPL, получим коэффициент Шарпа, равный 1.382776.

	Name_l	Name_2	Name_3	\| Name_4	Wt5_l	Wts_2 I	Wts_3 \|	Wts_4 \|	Port Returns	Port Risk	Sharpe_ ratio
341	WELL	DIS	MSFT	AAPL	0,001	0,004	OjOOS	Dj99	0,46256125 В	0,350543	1,319556657
25	ВАС	DIS	MSFT	AAPL	0,001	0,004	OjOOS	0^9	0,462535276	0,350593	1,319293221
320	WELL	MSFT	DIS	AAPL	0,001	0,004	OjOOS	0^9	0,462269189	0350454	1,319059376
4	ВАС	MSFT	DIS	AAPL	0,001	0,004	OjOOS	0^9	0,462243212	0,350504	1,31879603
233	DIS	WELL	MSFT	AAPL	0,001	0,004	OjOOS	Dj99	0,462093002	0,35052	1,318308861

Рис. 6. Фиксированные веса (0.001; 0.004; 0.005; 0.99)

Веса (0.1; 0.2; 0.3; 0.4) дадут результат в виде таблицы на рис. 7. Запуская программу для нахождения весов с набором активов WELL, DIS, MSFT, APPL, получим коэффициент Шарпа, равный 1.380239.

	Name_l	Name_2	Name_3	Na me_4	Wts_l	Wts_2 \| Wts_3	Wts_4	ort Return	Port Rkk	Sharpe_ratlo
341	WELL	DIS	MSFT	AAPL	o,l	0,2 0,3	0,4	0,3 36738	0,288 532	1,16707188
346	WELL	DIS	AAPL	MSFT	0,1	0,2 0,3	0,4	0,33211	0,286385	1,15966 25
25	ВАС	DIS	MSFT	AAPL	0,1	0,2 0,3	0,4	0,3 3436 5	0,291448	1,14725139
30	ВАС	DIS	AAPL	MSFT	0,1	0,2 0,3	0,4	0,3 29744	0,289189	1,14023865
233	DIS	WELL	MSFT	AAPL	0,1	0,2 0,3	0,4	0,322541	0,293 655	1,09836432
238	DIS	WELL	AAPL	MSFT	0,1	0,2 0,3	0,4	0,317961	0,291609	1,09036716

Рис. 7. Фиксированные веса (0.1; 0.2; 0.3; 0.4)

Таким образом, существует способ для более быстрого нахождения портфеля с наибольшим коэффициентом Шарпа, и он заключается в том, что можно выбрать активы при фиксированных весах и далее найти веса для данного наилучшего набора активов, чем находить веса для каждой комбинации из сочетаний активов.

Список литературы Нахождение оптимального портфеля ценных бумаг из набора активов

Борисова Л.В., Сагаева И.Д. Моделирование портфельного инвестирования: учеб. пособие. Саратов: ФГБОУ ВПО "Саратовский государственный университет им. Н.Г. Чернышевского", 2015. 22 с.
Дудов С.И. Оптимальное портфельное инвестирование. Саратов: ФГБОУ ВПО "Саратовский государственный университет им. Н.Г. Чернышевского", 2008. 312 с.

Статья научная