Нахождение остовного дерева минимального веса с применением алгоритма Краскала и алгоритма Прима
Автор: Батчаева З.Б., Биджиева А.Б., Турклиев Р.А.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 10 (19), 2018 года.
Бесплатный доступ
В последние десятилетия прослеживается существенное увеличение заинтересованности к теории графов. Рожденный более 200 лет назад в постановлении головоломок и развлекательных задач, он стал обычным, доступным и сильным инструментом для решения обширного диапазона важных практических задач. Теория графов рассматривается как раздел дискретной математики, исследующий свойства конечных множеств с установленными отношениями между их компонентами. Как прикладная дисциплина, теория графов дает возможность определить и изучить многие технические, экономические, биологические и социальные системы. Задача материала в том, чтобы следовать, в основном, главным понятиям и итогам теории графов, необходимым для постановки и решения задач управления организационными системами.
Теория графов, минимальное остовное дерево, алгоритм краскала, алгоритм прима
Короткий адрес: https://sciup.org/140263132
IDR: 140263132
Текст научной статьи Нахождение остовного дерева минимального веса с применением алгоритма Краскала и алгоритма Прима
Решение отдельных проблем может быть представлено в виде графа. К примеру, Женя, Дима, Максим и Алеша сыграли между собой по одной партии в шахматы. Какое количество партий было сыграно? Проанализируем решение задачи.
Женя сыграл партию с Димой, партию с Максимом и партию с Алешей – в целом три партии. Дима также сыграл три партии - с Женей, Максимом и Алешей. Однако, партию Димы с Женей мы уже посчитали. Остается добавить одну партию, которую сыграли Максим с Алешей. Исходя из этого искомое число партий равно значению выражения 3+2+1.
Нарисуем 4 точки, точки будут обозначать имена игроков. Затем соединим каждую точку с каждой точкой, который будет обозначать сыгранную партию. Посчитаем теперь количество отрезков. 4 стороны квадрата + 2 диагонали = 6 отрезков. Данная задача имеет интересную геометрическую интерпретацию, так называемый «полный граф». Решение представлено на рисунке 1.
Рисунок 1. Полный 4-вершинный граф
Ответом задачи будет 6 партий. Задачи естественнонаучного или экономического содержания иногда моделируются с помощью аппарата теории графов. Рассмотрим задачи о нахождении минимального остовного дерева минимального веса с применением алгоритма Краскала и алгоритма Прима.
В алгоритме Краскала применяется жадный подход к решению задачи, т.е. в любой момент выполнения данных алгоритмов имеется множество ребер E’, представляющее подмножество определенного минимального остовного дерева графа G. На каждом шаге алгоритмов из оставшихся ребер выбирается «лучшее» ребро, обладающее определенными свойствами, и добавляется к формируемому каркасу максимального веса. Одним из важных свойств любого ребра, добавляемого к E’, является его безопасность, т.е. то, что обновленное множество ребер E’ будет продолжать представлять подмножество некоторого минимального остовного дерева.

Рисунок 2. Нахождение остовного дерева минимального веса с применением алгоритма Краскала
Алгоритм Прима - это алгоритм построения минимального остовного дерева взвешенного связанного неориентированного графа.
Листинг программы на PascalABC реализующий алгоритм Прима.
Program commivoyger;
uses crt; var a: array [1..100,1..100] of integer;
posetil,q: array [1..105] of integer; n,z,c,i,j:longint;
Procedure commivoygergor;
Var ps,pe,max,min,k,I,j,x:longint;
Begin ps:=1; pe:=1; max:=0; c:=0; k:=z;
posetil[k]:=1; q[ps]:=k;
for i:=1 to n do for j:=1 to n do begin if a[i,j]>max then begin max:=a[i,j];
end ; end ;
max:=max+1;
while ps<=n do begin min:=max;
for i:=1 to n do if (a[k,i]<>0) and (posetil[i]<>1) and (a[k,i] c:=c+a[k,x]; pe:=pe+1; q[pe]:=x; posetil[x]:=1; ps:=ps+1; k:=q[ps]; end; c:=c+a[n,z]; n:=n+1; q[n]:=q[1]; end; begin clrscr; write('Введите количество городов:'); readln(n); write('Введите город с которого следует начать'); readln(z); for i:=1 to n do for j:=1 to n do begin if (i=j) then a[i,j]:=0; if (i readln(a[i,j]); a[j,i]:=a[i,j]; end; end; for i:=1 to n do begin for j:=1 to n do write(a[i,j],'':4); writeln; end; readln; commivoygergor; writeln('Путь: '); for i:=1 to n do write(q[i],'':4); readln; writeln('Длина'); write(c); writeln; readln; end. Рисунок 3. Результат работы программы алгоритма Прима Многие технические, экономические, биологические и социальные системы могут быть описаны и исследованы как прикладная дисциплина теория графов.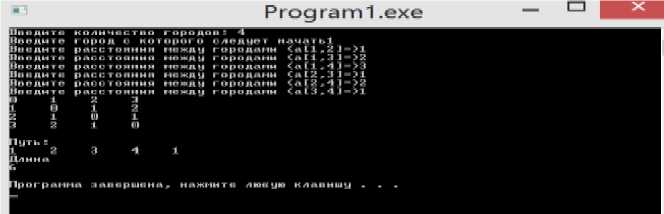
Список литературы Нахождение остовного дерева минимального веса с применением алгоритма Краскала и алгоритма Прима
- Белоусов А. И., Ткачев С.Б. Дискретная математика: учеб. для вузов. - М.: Издательство МГТУ им. Н.Э. Баумана, 2001.
- Емеличев В.А. и др. Лекции по теории графов. - М.: Наука, 1990.


