Нахождение периодических решений уравнения колебаний математического маятника

Рассмотрим модельный пример – уравнение колебаний математического маятника [2]

d² z .        / dz ^

---- + Sin z = 8 • f z,--  .

dt 2                  к dt )

Ответвляющиеся от z = 0

2 π

–

1 + /и

периодические решения уравнения

рассматриваются как решение системы dx

¹ = x 2 , dt

dx dt

x ³    x ⁵

- x. + -¹--- ^L + ...

¹    3 !    5 !

+ 8 • V a j1+ j 2 г 1

12 j ₁ j ₂ ^x 1 ^x 2 ^,

где x = z .

к

x=

С учетом обозначений   R ( х, 8 ) =

Г Х1 ^

к ^Х 2 )

, система (2) принимает вид

-

к

x _{1 +} x ₁

3 !    5 !

-

-

8 • E aJ1J2 xj x j1+ j 2 ^ 1               )

,

B=

Г о

к^{- 1}

о ) ,

где B : Е^ H Е₂ .

После применения

получаем x ( t )|__ т = x t 1 + v

С т

— = Bx - R ( x,s ) , dt

подстановки А. Пуанкаре t = —^т— , где v ( ^£ ) ^ 0 при £ ^ 0,

1 + V

к ^{1 +} V )

^d = ^f y ( т ). Тогда система (3) перепишется в виде

B y = цСу + R ( y,£ ) ,

где B y = ( B - C ) y , Cy = y ' ( т ) , B : £ H £ ₂, £_k = E_k + iE_k , k = 1,2. Множество нулей оператора

B имеет вид N ( B ) = { ф ( т ), ф ( т ) } , где ф ( т ) = ф = -j=

{—i ] к1)

e i , ф ^{( т} ) = ф = 4

(i л

2  ' )

e ^iт .

* Л*

*                „.*      *          *

I—H Е|     и B : £2 '—H £ ,

оператора имеет вид

Рассмотрим также сопряженные операторы B : Е₂

£ * =E * +iE * , k = 1,2. Множество нулей сопряженного

N ( B * ) = { р ( т ), у ( т ) } , где у ( т ) = у = ф, у ( т ) = у = ф .

Согласно следствию из теоремы Хана-Банаха в £ * существуют функционалы Y i , Y 2

такие, что [1, с. 337]

.Ф i ^,Y j)) = ⁶ ., , i,j = 1,2.

По тому же следствию из теоремы Хана-Банаха в £ ₂ существуют элементы Z j , z ₂ такие, что

((zk,V^ = \ s , ^k,s = 1,2.

I 2 n

Здесь ф₁ = ф , ф₂ = ф ; у = у, р₂ = У ; а ((g, g)} = — [ (f ( т ) ,g ( т )\ dт - значение функционала ^{2 П} 0

g(т) на элементе f (т). Используя лемму о биортогональности, получим у = у = zt = ф , i = 1,2.

Решение системы (4) будем искать по обобщенной лемме Шмидта. Введем оператор

B y ^ B y + ± i , z , , i = 1

где i,=((y,у,)}’ ,= 1,2.                                         (5)

i 1 = i , i 2 = i ,                                              ⁽⁶⁾

и запишем (4) в эквивалентной форме

B y = ^Cy + R ( y, £ ) + S tz i .

i= 1

Решение уравнения (7) представим в виде

y = w + S Z i V i , i= 1

где

w=w ^{( Z} 1 4 2 , Ф^£ ) =y 0010 У + У 0001 ^£ + S    У\ k₂ k l ^Z 1 k ¹ £^{k 2} V k ^£ l .                    (9)

k + k ₂ + k + 1 >  2

Подставляя (8) в (7), получим

B w = pw' + у£ф 1 '( т ) + yt₂V 1 ( т ) + R w +

S Zv i , ^£ •

к i = ¹          7

Подставив ряд (9) в систему (10), методом неопределенных коэффициентов найдем коэффициенты для w , а значит и для y .

Для нахождения системы разветвления подставим полученный ряд (9) в уравнения (5):

S j at 2 + S at 2 S L^ У£ = 0, m = >2 , i+j > 2                 i+j > 0       k+l > 1

где коэффициенты уравнения разветвления задаются так:

^Lij^mkl ^{=   y}ijkl ^{, γ}s   ^{, m = 1,2 .}

Для реализации метода неопределенных коэффициентов используется математический пакет Maxima. Для построения системы разветвления ограничимся третьим порядком коэффициентов.

Приведем значения ненулевых коэффициентов:

y 1010 =

(1Л . ei

2 к i 7

1 ( 1 1

, У 0110 =   „     . I ^e

—1

^iτ , y 1001 =

⁽ a 01 + ² a 10 ) + i ⁽ 2 a 01

—

^a 10

)  1 „it

442 к ⁽ 2 a 01 ^+a 10 ) ⁺ i ⁽ a 01 ^{+ 2} a 10 ) 7

e ,

y 0101 =

⁽ a 01 ^{+ 2} a 10 )   i ⁽2 a 01

—

^a 10 )

472 к ⁽2 ^a 01 ^+a 10 )   i ⁽ a 01 ^{+ 2 a} 10 L

— it            __ ¹

^e , ^y 3000 = ^2^

(—i/31

к 1  7

e ,

1        7\

У 2100 = ---т         ei

²¹⁰⁰    16^2 к— 1 + 2 i I

( 2 + i

\

y ¹²⁰⁰    1 6^2 к— 1 — 2 i

. e “ 7

, y 0300 =

1    ( i /3 1

3241 к 1 7

e-³ ' ,

y 1020

1 y 0201 =

⁽ a 20

—

a 02 ^{) —} ia 11

к

—

2a11

—

i ⁽ 2 a 20

—

2a )

a 02 77

e

,—2 it

,

y 2001 = 6

1 ^{(   (} a 20

—

a 02 ) ⁺ⁱ a 11

' к

—

2 a_u +i ( 2 a₂₀

—

² a 02 ) 7

e ² i ^T

^y 1101 ⁼

⁽ a ^{20 +a 02}'

к 0   7

,

У 1011

1   f ( ^{9 a} 01 + ^{2 а} 10 ) ^{+ i} ( ^{2 a} 01 + ^{9 a} i0 )

e "

8 V² v ⁽2 ^a 01    ⁷ a 10 )   i ⁽7 ^a 01 + ² a 10 ) у

У 0111

^{(  9 a} 01 ^{+ 2 a} 10 )   i ⁽2 ^a 01 ^{+ 9 a} 10 )

8 V² v ⁽2 ^a 01    ^{7 a} 10 ) ^{+ i (}7 ^a 01 ^{+ 2 a} 10 ) у

e "'

,

^y 1002

⁽ 4 ^a ₁₀   8 ^a ₁₀ a ₀₁ ) + i ⁽ 3 ^a ₁₀ + 4 ^a ₁₀ a 01

—

y 0102

16^2 Ц- 5 a 2 + 4 a₁₀a₀₁

■ ^a 10    ^{8 a} 10 ^a 01

16i/2 Ц- 5 a 2 + 4 a₁₀a₀₁

^{+ 3 a} 021 ) - i ⁽ 8 a 10 a 01 ^— i ⁽ 3 ^a 10 + ^{4 a} 10 a 01 ’ + 3 a 2 ) +i ( 8 a₁₀a₀₁

—

5 a 2. ) ^ .

e , ⁴ a 01 ) J

• ^{5 a} 01)'

• 1 ^{-    4} a 01L

, it

- it e .

Коэффициенты уравнения разветвления найдем по формуле (11). Приведем ненулевые

X I        2

f I — V

—

^a 10 ^^

—

1 ₂₂    1 ₂

— a}08 + —a0 e

—

- a ₀₁ e I +

+ f i

—

1 22 ^a 01 ^{eV + V +} „ ^a 10 ⁸

—

1            ₂     1 ₂

- ^a 01 ^a 10 ^{8  +} о ^a 01 ^e

^{+ 1 a} 10 ^{8 + 1} 1 ^f | 2 ] 2       8 у

= 0,

X I 2 f I — V

—

a108V

—

1 ₂₂    1 ₂

— a j _o e + —a ₀ j 8

—

—

f i

—

- ^a 01 ^£

—

^a 01 ^{eV + v +} _o ^a 10 ⁸ 8

—

1            2 1 2

— amaxoe +-a0 8

^{+ 1 a} 10 ^{8 + 1 f} | ² 1 2       8 у

= 0,

коэффициенты:

L (1) = 1001	((y 1001 ’ Y 1))       2( a 01     a 10 i ) ’		L (2) = 0101	((y 0101 > Y 2 ))	— 1 ( a 01 +a 10 i ) ,
L (1) = 1010	((y 1010 - Y1))   i ,		T ( 2) = 0110	((y 0110 - Y 2) ) =	— i ,
L (1) = 1002	((y 1002 ’ 71)) =		T ( 2)   = 0102	{{y 0102 - Y 2) ) =
=	22        2 a\a 01    a 10/   g V a 01 a 10    a 10	■ a 01 )	=	1 ( a 021 - a 1 2 0 ) +	— i ( 4 a 01 a 10 — a 10 8
L ( 1) = 1020	((y 1020 - 71))      1 ,		T ( 2)  = 0120	{(y 0120 - Y 2) ) =	-1,
L (1) = 2100	- i \\y 2100 - Y 1 / /   g ,		L ( 2)  = 1200	((y 1200 - Y 2) ) =	i — — 8
L (1) = 1011	(У 1011 - 7 1) ) = — a 10 — ia 01 ,		T (2) = 0111	((y 0111 ’ Y 2) ) =	— a10 +ia0 j.

^{- a} 021 1

записываем систему разветвления:

С учетом (6) и ^f = | ^ |²

Рассматриваем первое уравнение системы (12). Решение f = 0 отвечает тривиальному решению уравнения (1).

Пусть f ^ 0 . После сокращения первого уравнения на f и отделения вещественной и мнимой части [2, 3] получим:

Re :

^“

2          1 22

r — a\ q£R — ~ a q £

⁺ д ^a oi ^£    2 ^a oi ^{£ o},

Im :

-

^a oi ^£R ⁺ R + “^a io ^£ 8

-

2 ^a 01 ^a io ^£

^{+ 1} a oi ^{£ 2+ 1} a io ^£+ J ¹ % ^{| 2} = ^o.

Из второго уравнения выразим μ :

R = R ^(| % I ,^£ ) =

-

1 — a₀ £

~ a o ^e

₈   10

+ 2 ^a oi ^a io ^£

—

¹ 22 a_n £

₈   01

—

- ^a io ^£

—

¹ | % | 2 | , £ * — .

⁸ J       ^a 01

Подставив (13) в

первое уравнение, получаем приближенное редуцированное уравнение

разветвления:

| % | 4 + 2 £ ² ( a o2i +

a 2 ) | % | ² + ( a _x4) £ ⁴ — 15 a 4 £⁴ + 2 a 2 a ² ₀ £ ⁴ + 64 a 3 £ ³ — 8o a 2 £² + 32 a₀ £ ) = o.

Пусть % и % имеют вид [3]: % = r ( £ ) e‘ & , % = r ( £ ) e ^{1 0} , где &  e R . Следовательно, r = r ( £ ) = | % | .

Найдем решения биквадратного относительно | % | уравнения (14). Очевидно, имеет смысл только корень уравнения:

^| % ^| = J- г 2 ( й ² +а j ²₎) + ⁴^ 0i г ^{( a з} г ^^—4 « ² г ² + 5 « 0i г ^-2 j                       ⁽¹⁵⁾

при условиях

— £2 (a 2 + aio)+ 4 д/ a oi £ (a oi £3 — 4 a 4 £2 + 5 a oi £ — 2) > o, a0j£(a3j£3 — 4a2£2 + 5a0x£ — 2) > o.

Подставив (15) в (13), получаем

R = R(r (£)-£ ) = 1 •

2 1 — a₀ £

^{( a} oi ^a io ^{£ 2 — a} io ^£

—

aa £ — 4 aQ £ + 5a® £ — 2) ) .

Подстановка найденных ξ и μ в (9) и (8) дает приближенное однопараметрическое семейство периодических решений системы (4):

_{z      x}      Л sin a²

y ( T, £, & ) = 2 2         r

X cos a J

1 f   ( a _oi + 2 a _io ) cos a

— ( 2 a ₀ j — a_{l 0}) sin a

2^2 X— ( 2 a oi + a_w ) cos α

— ( — a_0l + 2 a ₀) sin a _y

r£ +

+

2 2 cos ^a

X — sin a J

rR +

1    ( 1/3 • sin 3 a⁴

1бЛ X cos 3 a

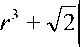
'"sin a j

_X — cos a J

2 rR

+

1   ( 2 cos a + sin a

+

8д/2 X— cos a — 2 sin a

\

J

3 ¹ r³ + —

(    ( a ₂₀ — a ₀₂) cos 2 a — a_{ ,sin 2 a

A

_X — 2 a _n cos 2 a — (2 a ₂₀ — 2 a ₀₂) sin 2 a _?

r ² £ +

+

( ^a 2» ^{a o} 2 j

X o J

r £ +

( ( — 9 a₀₁ + 2 a j ₀) cos a — ( 2 a₀₁ + 9 a_{x 0}) sin a ²

4^2X ( 2 a ₀j— 7 a j ₀) cos a + ( 7 a₀₁ + 2 a_{x 0}) sin a _y

r ^e +

+

² ( 4 a ₁ 2 ₀ - 8 a ₁₀ a 01 ) cos а - ( 3 a 2 + 4 a₁₀a 01 - 5 a 21 ) sin a ^Л

822 Ц-5 a 2 + 4 a₁₀a₀₁ + 3 a 2 ) cos a + ( 8 a₁₀a ₀[ - 4 a 2 ) sin a _?

rs2

где a = a ( t, 0 ) = т + 0 .

С учетом обратной замены y(т) |г = f (1+^) = у(т (1 + и)) d=f x(t) получаем x (t, s, 0) = 21

fsin el

( cos в J

r +

1 ^{f  ( a} 01 ^{+ 2 a} io ) ^{cos в  (} 2 ^a 01

222 ^— ( 2 a ₀₁ +a ₁₀ ) cos в — ( — a ₀₁

- a10 ) sin в " + 2a10 ) sin в,

rs +

+

+

+

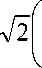
cos ^в l - sin в _?

гц +

1    1        3 в l

16^2 [ cos3 в J

f ² cos?₊ sin ^в i ^- cos в - 2 sin в J

r3

+ —

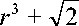
f- sin в l

-cos/?

^ cos в J

2 ru

+

f ^{( a} 20 - ^a 02 ) ^{cos 2 в} - ^a 11 ^{sin 2 в} "  у- 2 a_n cos2 в -(2 a ₂₀ - 2 a ₀₂) sin 2 в ₂

r2 s +

f a 20 -a

I 0

■02' J

r 8 +

1  f(-9a01 + 2a10) cos в-(2a01 + 9a10)sin вl

422 ^ ( 2 a ₀₁ - 7 a ₁₀ ) cos Д + ( 7 a ₀₁ + 2 a ₁₀ ) sin Д

r^s +

J

+

1 ^{f (} 4 a 20

- 8 a₁₀a ₀J cos в - ( 3 a 2 + 4 a₁₀a ₀j - 5 a 2 ) sin в

8x2 ^ ( - 5 a 2 + 4 a₁₀a₀₁ + 3 a 2 ) cos в + ( 8 a₁₀a ₀j - 4 a 2 ) sin в _?

rs2

где в = в ( t, Ц, 0 ) = (1 + Ц ) t + 0 .

С учетом 1 -го уравнения системы (2) и Xj = z, запишем полученные приближенные решения уравнения (1):

z i

r + ~7=1

22 1

[ ( a₀₁ + 2 a ₀) cos в - ( 2 a ₀j - a_{{ 0}) sin в ] rs +

48 2

sin ( 3 в ) • r³

-

⁺ 8?2 ⁽ 2 cos ^в + sin ^в ) r³ + ^{1 [(} a 20

-

a ₀₂)cos 2 в - a_n sin 2 в ] r ² s +

^{+ ( a} 20 ^{+ a} 02 ) ^{r 2 s +}      [ ^{( - 9 a} 01 + 2 a_{{ 0}) cos в - ( ² a₀₁ + 9 a ₁₀) sin в ] rus +

+ 8?2 [( 4 a²⁰ - 8 ^ ^0¹ ) cos в - ( 3 a 2 + 4 a₁₀a ₀, - 5 a ₀1 ) sin в ] rs ².

Учитывая, что уравнение (1) автономное, z(t, s, 0) в (16) - приближенное решение этого уравнения, то приближенным решением уравнения (1) также будет z (t + C, s, 0), где C e R, в = в (t + С,ц,0 ) = (1 + ц )(t + C) + 0.

Таким образом, мы получили двухпараметрическое семейство приближенных решений уравнения (1).