Нахождение прибыли экономико - математическим методом Монте - Карло в среде QlikView

В данной статье будет представлен стартап компании по производству индивидуальных чехлов для мобильных телефонов из натурального дерева. Для расчета рентабельности будущего бизнеса нужно сымитировать будущею прибыль компании. Возьмем в расчет то, что приблизительная стоимость товара будет в диапазоне от 1000 до 2000 руб, с вероятным значением 1800 руб. Количество заказов в месяц будет приблизительно 120 единиц товара, а количество заказов в год будет определяться как сумма количества заказов в предшествующем месяце и его изменения, которое находится между 5% и 8%. Так же нужно будет вычесть от чистой прибыли затраты на производство, они будут составлять 20% от стоимости товара. По итогу должна сформироваться приблизительная прибыль предприятия в год, так же нужно будет определить наилучший и наихудший результаты и определить среднее значение чистой прибыли. В планах у компании получать прибыль 2 000 000 рублей в год, в ходе решения задачи нужно выявить вероятность получения данной прибыли.

Для начала создадим файл Exsel в котором будем задавать входные параметры для решения задачи:

Таблица 1 Количество заказов

Q	Qi
120	Q0
-0.05	Q1
100	Q2

, где Q – количество заказов, Qi – порядковый номер года.

Таблица 2 Данные о стоимости товара и вероятности стоимости товаров

Товар	P1	p1
1	1400	0.25
2	1800	0.5
3	2000	0.25

, где Товар – номер товара, Р1 – стоимость товара, р1 – вероятность такой стоимости товара.

Таблица 3 Данные о количестве месяцев

iQ	iP	iG
1	1	1
2	2	2
3	3	3
4	4	4
5	5	5
6	6	6
7	7	7
8	8	8

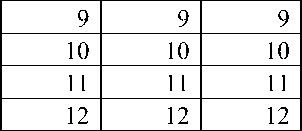
, где iQ – количество месяцев для расчета массива количества заказов по месяца, iP – количество месяцев для расчета массива стоимости заказов по месяца, iG – количество месяцев для расчета суммарной прибыли за год.

Данные по затратам и количеству реализаций (Таблица 6)

Таблица 4 Данные по затратам и количеству реализаций f        k1       k2

0.2    1000   10000

, где f – затраты, k1 – количество реализаций в месяц 1000, k2 – количество реализаций в месяц 10000.

Следующим шагом будет создание скрипта в среде QlikView. Заходим в редактор скрипта и начинаем загружать данные для задачи, скрипт будет выглядеть так – Рисунок 1. В обозревателе таблиц мы можем видеть, что таблицы не связаны между собой, для решения задачи это и не нужно (Рисунок 2).

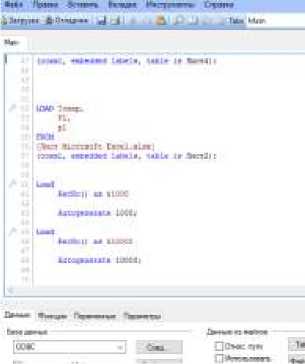
Рисунок 1 Создание скрипта

Так же на Рисунке 1 в скрипте можно увидеть автоматический генератор чисел от 1 до 1000 и от 1 до 10000 – эти измерения нам позже пригодятся для решения задачи.

Решение начинаем с нахождения среднего значения стоимости товаров:

• 1.    Создадим сводную таблицу;

• 2.    Выберем измерение «Товар»;

• 3.    Перейдем на вкладку «Выражения» и напишем формулу для расчета.

Формула будет выглядеть так:

sum(TOTAL <Товар> P1*p1)          (1)

, где TOTAL – означает, что вычисление выполняется по всем возможным значениям, и суммируется по выражению P1*p1. В результате мы получим таблицу с результатом Рисунок (2):

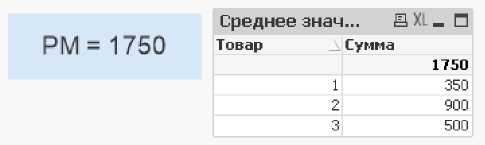
Рисунок 2 Среднее значение стоимости товаров

На рисунке выше видно, что стоимость товара была просуммирована с вероятностью и итогом как раз вышло среднее значение стоимости товара. Рядом с таблицей для наглядности было создано текстовое поле со значением.

Дальше находим среднее квадратичное отклонение стоимости:

• 1.    Создадим сводную таблицу;

• 2.    Выберем измерение «Товар»;

• 3.    Перейдем на вкладку «Выражения» и напишем формулу для расчета:

На языке QlikView формула будет выглядеть так: (Sum(TOTAL<Товар>((sqr(P1)*p1)))) - (sqr(sum(total Aggr(sum(P1*p1),Товар))) * sum(p1))                                                      (2)

Для правильного представления формулы разобьём её на более мелкие и понятные части:

• 1.    Откроем скобки;

• 2.    Умножим обе части на p1 i ;

• 3.    Возведем обе части в квадрат;

• 4.    В таблице получился результат общий для всех товаров = 47 500 (Рисунок 4), для правильного решения мы должны вычислить квадратный корень из этого числа, в сводной таблице это будет сделать невозможно. Для решения

создадим текстовый объект и вставим формулу туда, но перед формулой добавим функцию для вычисления квадратного корня – sqrt. Формула приобретёт следующий вид:

sqrt((Sum(TOTAL<Товар>((sqr(P1)*p1))))          -          (sqr(sum(total

Aggr(sum(P1*p1),Товар)))* sum(p1)))(3)

Среднее квад... В XL ■ □

• I                       Товар           //sqrt((... А

  DP-217,94                 47500

1          -275625

2           88750

3         234375

Рисунок 3 Квадратичное отклонение стоимости

• В итоге в текстовом поле (рисунок 3) мы видим значение средне квадратичного отклонения стоимости.

Теперь нужно найти изменение количества заказов в месяц – равномерное распределение.

Массив количества заказов по месяцам (dQ(k)) - находим рандомное распределение чисел в диапазоне от Q1 до Q2.

Формула на языке QlikView: (Rand()+(Q1))*Q2               (3)

, где k – количество реализаций – размер случайной совокупности.

Результат вычислений можно увидеть на рисунке 4.

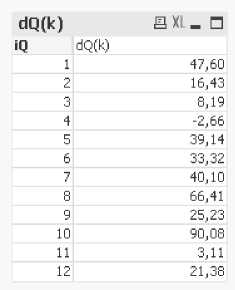
Рисунок 4 Массив количества заказов по месяцам (dQ(k))

Массив стоимости заказов по месяцам (P(k)) - находим рандомное распределение чисел в диапазоне от PM до DP.

Формула на языке QlikView:

Floor(rand()    *     (sum(TOTAL    <Товар>    P1*p1)))

+

(sqrt((Sum(TOTAL<Товар>((sqr(P1)*p1))))-(sqr(sum(total

Aggr(sum(P1*p1),Товар))))* sum(p1)))

Результат вычисления можно увидеть на рисунке 5.

Р(к)		BXL_ □
iP	Р(к)
	1	626,94
	2	356,94
	3	1 537,94
	4	264,94
	5	830,94
	6	414,94
	7	1 611,94
	8	389,94
	9	1 872,94
	10	787,94
	И	1 537,94
	12	1 886,94

Рисунок 5 Массив стоимости заказов по месяцам (P(k))

Добавим через загрузку скрипта возможное значение суммарной прибыли: для а) k = 1000 реализаций, б) k = 10 000 реализаций.

Результат можно посмотреть на рисунке 6:

Прибыль при kl = 1000 В XL _ □

438:	435 945
439	1 338 945
440	1 588 945
441	670 945
442	1 229 945
448:	1 526 945
444	1 457 945
445	368 945
446	780 945
447	1 022 945
448:	1 402 945
449	1 084 945
450	665 945
451	1 881 945
452	524 945
453	1 428 945
454	235 945

Прибыль при к2 = 10000 В XL_ □

kioooo	при к? = 10000
8731	1 910 125
8732	1 416 463
8733	221 712
8734	1 072 558
8735	1 552 300
8736	1 576 299
8737	1 279 354
8738	891 242
8739	1 866 054
8740	282 294
8741	830 483
8742	324 399
874:3	1 501 159
8744	1 914 736.
8745	737 682
8746	1 458 411
8747	587 668:

Рисунок 6 результат вычисления прибыли, при разном количестве реализаций

Для нахождения статистических показателей, выгрузим данные и таблиц (рисунок 6) и загрузим обратно в модель через скрипт и в отдельных таблицах найдем эти показатели (рисунок 7):

Статистические показатели при kl =	1ООО	В XL - □
Среднее		1 084 995
Минимальное		217 945
Максимальное		1 966 945
Ср е д неквадр а т ичн о е откл онен-е		508 213
Коэффициент ковариации		0,047
Статистические показатели при к2 =	1ОООО	BXL_ □
Среднее		1 224 356
Минимальное		242 306
Максимальное		2 106 461
Средне кеадратичноеотклоне ние		559 237
Коз ффи ц и ент ко б а риа ц и и		0,046
Вероятность прибыли быть меньше 2000000		1,09

Рисунок 7 Статистические показатели, при разном количестве реализаций

Проверим вероятность прибыли быть меньше 2 000 000 руб. составит: 1.9%.

Наглядно это можно увидеть на рисунке 8:

Статистические показатели при 1	к2 = 1ОООО           BXL_ □
Среднее	1 224 356
Минимальное	242 306
Максимальное	2 186 461
Среднеквадратичное отклонение	559 237
Коэффициент ковариации	0,046
Вероятность прибыли быть меньше 2000000	1,09

Рисунок 8 Вероятность прибыли быть меньше 2 000 000 руб

Для расчета использовалась формула QlikView:

((Rand()*(Avg ([при k2 = 10000])))+(Stdev ([при k2 = 10000])))/2000000 (5) , где Avg – среднее число массива, Stdev – среднеквадратичное отклонение, 2 000 000 – вероятностное значение прибыли.

Вся информация результатов исследования прибыли в среде QlikView для сценария распределения входных переменных показана в Главе 3, где представлены решение задачи и результаты моделирования для входных данных из таблицы и двух случайных совокупностей: 10000 и 1000 реализаций. Как видно, 1000 и 10000 реализаций дают очень близкие результаты по числовым характеристикам. Как правило, требуется знать наилучший и наихудший сценарии возможных событий. Статистические показатели для ожидаемой прибыли: минимальное значение - наихудшее (242 306 руб.), максимальное значение - наилучшее (2 186 461 руб.), среднее – ожидаемое значение (1 224 356 руб.), представленные для двух случайных выборки, включающих 1000 и 10000 реализации модели практически не отличаются. Разброс значений относительно среднего (коэффициент вариации) составляет приблизительно 5%. Риск получить прибыль, отличную от суммы 2 000 000 руб. равен 1.9 %.

После решения задачи и сравнения итогов был сделан вывод, что и среда QlikView не совсем пригодна для решения подобного рода задач. Задача решена с использованием специальных функций QlikView для работы со случайными величинами. Но есть все же функции программы, которые могут помочь в ведении бизнеса. Среда QlikView интегрируется со многими бухгалтерскими программами, к примеру, CRM или BW – кубы (продукты компании SAP), с помощью коннектора, данные загружаются в QlikView и там уже можно вести аналитику по количеству заказов, по прибыли, так же можно строить прогнозы на другие месяца, по итогам прошлых месяцев. Строить наглядные графики и дашборды. Смотреть зависимость между данными, как известно среда QlikView имеет ассоциативный поиск данных и относится к программам BI. Так что это может очень пригодиться в работе компании.