Наложение изображений со смешением границ с помощью преобразования Пуассона

Поставлена задача смешения краев накладываемого изображения с целевым изображением. Обозначим целевое изображение, как А, накладываемое изображение, как В. На рис. 1 представлено схематическое изображение областей. Необходимо чтобы градиент изображения А в области изображения В равнялся градиенту В. Восстановление информации о цвете в области В происходит за счет градиента в области В и цветовых данных изображения А на границе области В.

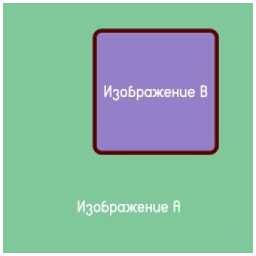
Рис. 1 - Схематическое обозначение областей накладываемого и целевого изображения

Таким образом для получения соединенного изображения необходимо восстановить изображение по его градиенту, что является задачей Пуассона [1].

Пусть граница области В определяется следующим образом:

H (x,y)= A (x,y) V(x,y) е 9 В

Тогда градиент изображения В будет вычисляться как:

I^B (x,y) | = 4В⁽х, у) — В⁽х — 1, у) — В⁽х + 1,у) — В⁽х,у— 1) — В(х,у + 1)

Составим уравнения Пуассона:

\N\H(x,y) —     ^     H(x + dx,y + dy)

(dx,dy)+(x,y)en

—

^     А(х + dx, у + dy)

(dx,dy)+(x,y)edQ

^     В(х + dx,y + dy) — В(х,у)

(dx,dy)+(x,y)enudn

,где

(x,y) - координаты текущего пиксела,

N - число соседних пикселов без включения границ,

(dx,dy) - координаты соседних пикселей принимающие одно из множества значений {(-1, 0), (1, 0), (0, -1), (0, 1)}.

Таким образом мы получаем систему с L неизвестными, где L - число пикселей накладываемого изображения. Решение системы можно произвести любым доступным методом [2] [3].

Приведем пример результатов вычислений. Исходное изображение и накладываемое с выбранной областью наложения представлены на рис. 2., результат показан на рис. 3.

Рис. 2 - Накладываемое и целевое изображение

Рис. 2 – Результат наложения