Нанодвойникование мартенситных кристаллов и теория адаптивных фаз

В сплавах с эффектом памяти формы, испытывающих мартенситное превращение исходной ОЦК-фазы, обнаружены длиннопериодные мартенситные структуры, природа которых остается не ясной. Так, в сплавах системы Ni-Al с понижением содержания никеля вместо ГЦТ-мартенсита образуется длиннопериодная моноклинная структура 7М с символом Жданова (52), которую можно трактовать как гипотетическую ГЦТ-структуру с чередующимися прослойками матричной и двойниковой ориентировки толщиной в пять и два слоя, соответственно (рис. 1). В сплаве Ni2MnGa аналогичная структура в силу атомного упорядочения обозначается как 14М.

Относительное смещение 5₀ плотноупакован-ных слоев в моноклинной структуре 7М превосходит величину а/3, характерную для идеальных плотноупакованных структур, и может быть представлено как 5₀ =(а/3)(1 + £). Величина моноклинных искажений е для сплавов NiAl и Ni₂MnGa лежит в интервале значений 0,26-0,28 [1,2].

В ряде работ образование структуры 7М объясняют особенностями предпереходного состояния ОЦК-фазы, а именно, размягчением мод колебаний с волновым вектором q = 1/7(011] либо ангармоническими смещениями шестислойных пачек слоев (011) с их упорядоченным расположением через один слой [1].

Альтернативная гипотеза о природе структуры 7М и других длиннопериодных мартенситных структур, известная как теория адаптивных фаз, предложена в работе [3]. Суть теории адаптивных фаз заключается в следующем. Образование мартенситных кристаллов сопровождается возникновением упругой энергии, обусловленной несоответствием кристаллических решеток на границе раздела матричной и мартенситных структур. Один из способов минимизации этой упругой

энергии - формирование мартенситных пластин, состоящих из квазипериодических пластинчатых доменов двух ориентировок толщиной d_x и d₂, находящихся в двойниковом соответствии. Отношение их объемных долей

1 - <в0 а2

должно быть таким, чтобы обеспечить макроскопически неискаженную плоскость габитуса мартенситных кристаллов. Согласно [3] в случае низкой энергии двойниковых границ толщина доменов уменьшается до минимальных значений, что равносильно формированию промежуточных адаптивных структур с периодом 2 = d_x + d₂.

В работе [3] концепция теории адаптивных фаз использована для описания превращения исходной кубической фазы с параметром решетки а_с в тетрагональную структуру с параметрами a_t и c_t . Считалось, что мартенситная пластина со

стоит из чередующихся тетрагональных доменов двух двойниковых относительно плоскости (110)с

ориентировок с осями тетрагональности, образующимися из направлений [Ю0]с и [010]с, соот

ветственно. Тогда в приближении линейной тео

рии упругости тензор усредненной макроскопической деформации принимает следующий вид:

% 0

е_х 0

< Ц®) >= СО

(о о

0 + (1 - о) 0 е3

a J 0 0

О'

о • (2)

е1>

Здесь е_х = (,a_t - а_с) / а_с, е₃ =(c_t -а_с)/а_с, со -доля

доменов первой ориентировки. Для обеспечения свободной от напряжений границы раздела между кубической матрицей и мартенситным кристаллом деформация (2) должна являться деформацией с инвариантной решеткой. Это возможно при выполнении двух условий: во-первых, один из эле-

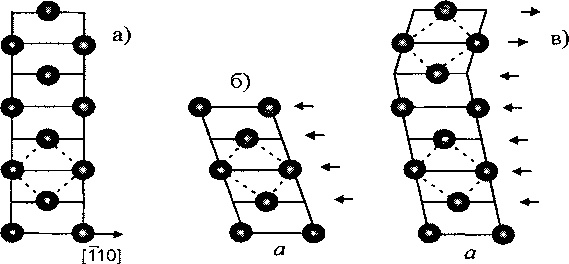
Рис. 1. Исходная ОЦК-фаза (а) и мартенситные структуры ГЦТ (б) и 7М (в)

ментов (2) обращается в ноль, во-вторых, два других элемента (2) должны иметь разные знаки, Первое условие определяет требуемую объемную долю пластин первой ориентировки

Второе условие выполняется, если элементы е_х и е₃ имеют разные знаки, причем [% | > Ц |.

Плотность сдвигов упаковки (2/7=0,286) в структуре 7М близка к рассчитанной в [3] доле двойниковой ориентировки (~0,3), требуемой для обеспечения инвариантной плоскости габитуса мартенситных кристаллов при ОЦК->ГЦТ превращении. На этом основании в [3] сделан вывод о том, что образование миниатюрных прослоек двух ориентировок ГЦТ-структуры толщиной в пять и два слоя, формирующих структуру 7М - результат стремления системы в максимальной степени понизить упругую энергию межфазной поверхности. В этом смысле структура 7М, по мнению авторов [3], является адаптивной фазой. Однако в расчетах [3] использовалось допущение о бесконечно малой величине деформаций превращения, так что сами расчеты и выводы [3] требуют уточнения.

Выполним точный расчет кристаллографических характеристик мартенситного превращения исходной ОЦК - структуры без использования приближений линейной теории упругости. Будем считать, что деформация превращения осуществляется двумя последовательными деформациями с инвариантными плоскостями:

T = SrS2.                           (4)

Первая деформация S] представляет собой сдвиг [101](110)£ и небольшую дилатацию, необходимые для преобразования плоскости (110)^ в плотноупакованные плоскости мартенситной структуры. Деформация S2 обеспечивает правильную укладку плотноупакованных слоев в мартенситной структуре за счет однородного сдвига по системе [110X110)^. Деформация S2 на макроскопическом уровне компенсируется за счет скольжения частичных дислокаций по плотноупакованным плоскостям мартенсита. Соответственно, плоскость габитуса мартенситного кристалла определяется непосредственно как инвариантная плоскость деформации S].

Известно, что однородную деформацию можно задать матрицей S = I + b nr, где I - единичная матрица, b - вектор смещения, п - нормаль к плоскости смещения. Используя это представление, запишем выражения для деформаций Sj и S2 в рассматриваемом случае:

S] =1+[1 + С1,Т + с2,с3][1,1+с4,с5]г,       (5)

S2 =I + c6[T10][110f.                    (6)

Выберем в исходной ОЦК - решетке орто ромбическую ячейку - «прообраз» будущей решетки мартенсита. Орторомбическая ячейка (110)^ задается базисными векторами х,п = а[110]^ , ут=а[001]^, лежащими в плоскости (110)^, и вектором zm, который трансформируется в ось ст мартенсита. Выбор вектора zm зависит от типа образующейся мартенситной структуры. Деформация превращения T = S]-S2 преобразует введенные выше вектора хт , ут, гт в орторомбические базисные вектора am, bm, cm мартенситной решетки. Соответственно, неизвестные параметры с, деформации Т легко найти численным решением следующей системы уравнений: (тхт)(ТУт) = 0,          |T-xm| = a„,

^■^•^•^^^„co^PY |т-у„| = 6_т, (7) (Tz„)-(T-y_m) = 0,            |T-z_m| = c_m.

Первые три уравнения в системе (7) отражают ортогональность векторов а_т, b_m, а также тот факт, что в моноклинных структурах ось с_т мартенсита составляет с осью а_т угол р , зависящий от величины моноклинных искажений е . Три последних уравнения обеспечивают совпадение абсолютных значений этих векторов с их экспериментальными значениями.

После нахождения неизвестных с, численным решением системы (7) непосредственно определяются индексы плоскости габитуса

Г = (1,1+с4,с5),                         (8)

направление и величина макроскопического сдвига s = [l + q, 1+с2,с3],                        (9)

величина деформации при инвариантной решетке

О d х , и плотность сдвигов упаковки (доля двойниковой ориентировки)

®о=", (11) о требуемая для компенсации сдвиговой компоненты деформации превращения S2. Здесь d - межслоевое расстояние плотноупакованных плоскостей мартенситной структуры; 5 = (ат / 3)(1 - 2^) -вектор Бюргерса частичной дислокации.

Ниже (см. таблицу) приведены кристаллографические характеристики мартенситных превращений сплавов Mi62 5А137 5 и Ni2MnGa , рассчитанные с использованием параметров элементарных ячеек, приведенных в работах [1,2].

Рассчитанные плоскости габитуса и ориентационные соотношения хорошо согласуются с экспериментальными данными. Наиболее важный результат выполненных расчетов заключается в том, доля слоев в двойниковой ориентировке, требуемая для обеспечения инвариантной плоскости габитуса

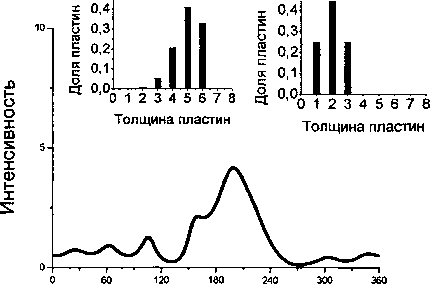
Переменная обратного пространства

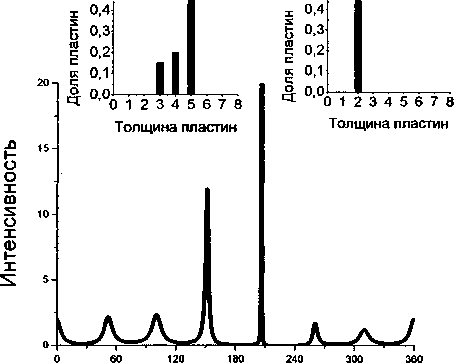
Переменная обратного пространства

Рис. 2. Профили интенсивности, рассчитанные по (9) при разной дисперсии толщины двойников системы (111 )[112] в ГЦТ-структуры с величиной искажений е = 0,264

Кристаллографические характеристики ОЦК->7М превращения

Кристаллографическая характеристика	Сплав Ni625Al375	Сплав Ni2MnGa
Плоскость габитуса	(-8,8, 1, -11,8)	(-5,2, 1, -7,8)
Угол между плоскостями (110)^ и (Ю0)т	2,3°	2,7°
Угол между направлениями [110]^ и [100]т	2,9°	3,6°
Величина макроскопического сдвига	0,109	0,135
Величина деформации с инвариантной решеткой	0,111	0,109
Требуемая доля двойниковых прослоек	0,348	0,326
Требуемая доля двойниковых прослоек по расчетам [3]	0,29	0,30

(0,348 - для сплава Ni62 5А137 5 и 0,326 - для сплава Ni2MnGa) значительно отличается, как от оценок [3] (0,29-0,30), полученных в рамках приближения бесконечно малых деформаций, так и от значения 2/7 = 0,287, соответствующего структуре 7М. Соответственно, нет оснований трактовать структуру 7М в указанных сплавах как адаптивную фазу. Скорее в качестве такой адаптивной фазы должна была выступать структура 9М (21)3 с плотностью сдвигов упаковки 1/3 = 0,333, образующаяся, например, в медных сплавах. Однако в сплавах на основе никеля структура 9М не образуется.

Дополнительные доводы против гипотезы об адаптивной природе мартенситной структуры 7М в никелевых сплавах следуют из анализа их дифракционных картин. Ниже представлены теоретические профили интенсивности ГЦТ-кристалла, содержащего двойники системы (111)[112] с долей 2/7 (рис. 2). Видим, что семь отражений на периоде обратной решетки, свидетельствующие об образовании длиннопериодной структуры 7М, возникают только при предельно низкой дисперсии толщины пластин (7) < 0,2).

Трудно представить, что единственная причина - стремление понизить упругую энергию межфазной поверхности - может обеспечить столь высокую регулярность двойниковой структуры, тем более что доля (2/7) сдвигов упаковки в ней не строго соответствует требованию неискаженной плоскости габитуса.

Таким образом, выполненные кристаллографические расчеты и моделирование дифракционных картин структуры 7М и позволяют утверждать, что вывод работ [2, 3] об адаптивной природе мартенситной структуры 7М в сплавах Ni62 5А137 5 и Ni2MnGa является ошибочным. Истинные причины появления этой структуры связаны с особенностями предмартенсиного состояния, а именно с размягчением моды колебаний с волновым вектором q = 1 / 7[011].

Работа поддержана грантом РФФИ 05-08-33707-а.