Наноматериал повышенной прозрачности

Большое внимание привлекает в последнее время исследование оптических свойств искусственных материалов, состоящих из различного рода наноразмерных объектов, внедренных в некую матрицу, и получивших в литературе название «метаматериалы» [1–4]. Указанный интерес обусловлен возможностью достижения ряда необычных эффектов, обусловленных композиционной структурой среды, а также спецификой рассеяния света наночастицами. Действительно, за счет варьирования материальных и геометрических параметров системы достигается, например, возможность получения сред с гигантским, сверхмалым либо отрицательным показателем преломления [1,5,6], а также показателем преломления, реальная часть которого близка к единице [7].

прямое решение уравнений Максвелла, как то: метод конечных элементов (FEM) [11], метод конечных временных разностей (FDTD) [12,13], метод связанных диполей (CDA) и пр.

В данной работе нами предлагается аналитический подход к описанию оптических свойств упорядоченных нанокомпозитов, позволяющий представить агрегат из наночастиц произвольной толщины в виде математической бесконечно тонкой границы раздела, обладающей нефренелевскими коэффициентами отражения и пропускания. При этом, для описания оптических свойств системы, становится возможным использовать простые соотношения Эйри для нескольких границ раздела, одна из которых является «мнимой» и характеризует «сжатый» наноагрегат.

1.    ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим структуру, показанную на рис. 1 и воспользуемся методом интегральных уравнений [14–16]. Поле, создаваемое композитной средой в каждой точке пространства, может быть записано в следующем общем виде:

_r      P ( r ' , t — RI c )   .

— ( r , t ) = — ( r , t ) +J robot —--------У Р '+

V R

(i()-e — .„(г, t — R./C , '    -fj^J-Ldiv', (1)

3 Л_г^£j +--) rotrot--;

⁴ ™ j =T V j E j (

R j

m

где — I ( r , t ) = — ₀ I exp ( i k ₀ r — i to t ) - внешняя волна в точке наблюдения r , k ₀ - волновой вектор. Первый интеграл в правой части определяет поле, создаваемое средой-матрицей с поляризацией P , пропорциональной падающему на поверхность среды полю, и диэлектрической проницаемостью £ m . При этом R = |r — r '| - расстояние от точки интегрирования r ' , расположенной внутри среды, до точки наблюдения, V – объем среды, с – скорость света в вакууме, аргумент ( t — R I C ) характеризует запаздывание со-

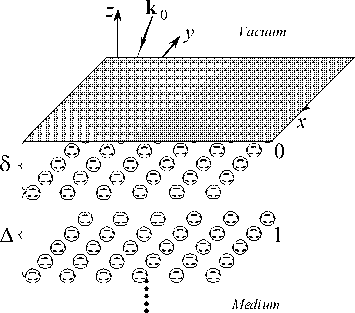
ды является линейной функцией напряженности поля. Помещая начало координат на поверхность среды-матрицы, а точку наблюдения в центр i –й частицы, имеющий радиус-вектор r i (см. рис. 1), запишем эффективное поле:

E f ^{( r} i , t ^{) —}

■»>

■»>

j *

V j

3 Е—Е v m rotrot

4 яЕ+ 2 Е mj — 1"

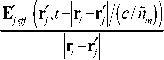
-dV j +

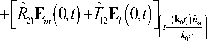
Рис. 1. Геометрия системы. Композит состоит из 5 + 1 слоёв с расстоянием д между ними. Расстояние между поверхностью среды и плоскостью, проходящей через центры наночастиц нулевого слоя - 5

где n_m — л/Е m , первый член в правой части представляет собой суперпозицию полей, создаваемых наночастицами ансамбля в центре i- й. Второе слагаемое определяет полное поле (с учетом

ответствующей величины. Третий член в (1) определяет поле, создаваемое J взаимодействующими наночастицами c комплексной диэлектрической проницаемостью Е ( г ,-) и объемом V_; . jj           j

При этом R j — r — r j , r j - точка интегрирования внутри j- й наночастицы относительно начала координат. Поле E jeff , фигурирующее в выражении (1), представляет собой волну, действующую на каждую точку внутри j- й наночастицы с учетом полей, переизлученных атомами всех наночастиц. Назовем поле E jeff эффективным. При этом E jeff имеет две составляющие: внешнюю (или действующую со стороны окружения) и внутреннюю, определяющую взаимодействие атомов внутри самой наночастицы и отвечающую за формирование диэлектрической проницаемости среды [17]. Учет внутреннего поля приводит к разделению уравнения (1) на локальное и нелокальное; при этом первое дает известную формулу Лорентц – Лоренца. Поставленная граничная задача сводится, таким образом, к поиску эффективных полей, действующих на каждую наночастицу со стороны ее окружения (обозначим их E jef ).

Рассмотрим композит из одинаковых однородных нанокластеров ( Е j ( r ) — Е ), бесконечно протяженный в плоскости xy, внедренный в по-лубесконечную среду. Воспользуемся приближением длинных волн [18]:

к0a, k0Re(n) a, к0Im (n) a 1 << 1,      (2)

где n _— д/g , означающими, что напряженности Е I и E , ef однородны во всем объеме сферической частицы радиуса a . При этом ограничимся случаем, когда вектор поляризации частиц и сре-

поля, излученного самим слоем и отраженного от границы раздела среда-вакуум), падающее на i- ю частицу извне; T , R – тензоры френелевских коэффициентов пропускания и отражения границы раздела, а порядок индексов показывает направление падения исходной волны («12» – из вакуума в среду, «21» – из среды в вакуум); E m – падающее на границу эффективное поле, аргу-

мент

t

^^^^^^^»

n r )n

0im k0c

характеризует запаздыва-

ние на время прохождения волной расстояния от начала координат до центра i- й наночастицы. Выражение для E m примет следующий вид:

E m ( 0, t ) —

3 Е—Е m

4 л Е+ 2 Е m

^rotrot J j—1            V,

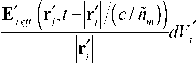
Решая в общем виде систему из уравнений (3)–(4), получим значения эффективных полей в центре каждой из наночастиц, а также эффективного поля, падающего из среды на границу раздела. Поле, отраженное от композита, примет вид согласно (1)–(4):

E r ( R , t ) — 7 R 12 E i ( 0, t ) exp ( i k o R ) + T 21 [ E „ ( 0, t ) ] r t_—^ ^ , (5)

I ko c J где R – радиус-вектор точки наблюдения, первый член в правой части характеризует френелевское отражение от чистой (в отсутствие наночастиц) среды, а второй – вклад нанокомпозита в отраженную волну. При этом учтено, что Em имеет сложную структуру, отличную от плоской волны и, соответственно, запаздывание на время (k 0 R) / к 0c будет характеризоваться изменением и фазы, и амплитуды поля.

2. МЕТОД «МНИМОЙ ГРАНИЦЫ»

Рассмотрим поле, создаваемое j -й наночастицей, расположенной в вакууме, в некоторой точке наблюдения R вне ее объема. Интеграл, отвечающий соответствующей напряженности в (1),

может быть легко вычислен [14–16]. В результате получено следующее соотношение:

^E j, „ ( ^R , t ) = “ p^fj ( ^R ) ^E jf ( , t ) , (6)

где введены обозначения:

( 2

f, ⁽ R ⁾ = exP ⁽ ik о R ⁾ I -^3 ^-V R

2 ik 0

R ² J^,

f ^ ( R ) = exp ( ik о R ) - -L +    +    I ,

R R R I a = a3 p

g - 1

.

8 + 2

Очевидно, что если окружающая частицу среда не является вакуумом, величины g и n в (6) -относительные, а не абсолютные, а также необходима замена к 0 —— к 0 n m .

Преобразовывая интегральные слагаемые в (3), (4) в соответствии с (6)–(7), получим следующую систему уравнений для полей:

E' eff (ri, t ) = « p T f (|Г - rj I) Ejef ( rj, t ) +

j = 1, ^j *

+ [ Tf 2i E „ ( 0, t ) + T 2 E I ( 0, t ) ] ( t ( k 0 , ) n „ , , (8)

V      ^к 0 c )

то

^E m ^{( 0}, t ⁾ = « P T ^f, (| j ) ^E jeff ⁽ r j , t )• (9) j = 1

Прямое вычисление E i eff из системы уравнений (6)–(9) не представляется возможным, поскольку, ввиду наличия в (7) членов, пропорциональных 1/ R , взаимное поляризующее влияние частиц является дальнодействующим [18,19]. В связи с этим, предлагается использовать метод послойного расчета полей в нанокомпозите, заключающийся в разделении конечного по толщине агрегата на S + 1 взаимодействующих монослоев [15] (см. рис. 1).

Расположим систему координат таким образом, чтобы центр рассматриваемой i - й наночастицы имел координаты 5 + ; A = ( 0,0, -S-;A ) , где S — расстояние от поверхности до плоскости, проходящей через центры наночастиц первого слоя, A — расстояние между слоями (рис. 1). При этом система уравнений (8)–(9) примет вид:

S

e; = apE; Ap; + T apEk C; ((n - к) A) +

к = 0, к *;

+ [ ^^ 21 E m ( 0, t ) + T 12 E , ( 0, t ) ] ( t _- k 0 ( 5. A ) n m

V           ^к 0 c       .

S

Em (0, t ) = a p T e;C;(-6 - кA),   (11)

к = 0

где индексы к , ; соответствуют номеру слоя. Первому слою присвоен номер 0, а также учтено, что, так как все кластеры в пределах одного слоя находятся в равных условиях, выполняется равенство: | E i _; ef | = | E _>; ef | = | E _; | . Разность фаз E i _; и E , _; учтем в соответствии с принципом трансляционной симметрии [20, 21], согласно которому напряженность поля, падающего на слой из наночастиц, удовлетворяет условию:

E (r,) = E (0) exp (iqrj), где j = 1, 2... то, а вектор q = (qx,qy,0), где qx = к0sin0,cos^ , qy = к0sin0Isin^ , 0I - угол падения, ф - угол между координатной осью x и

плоскостью падения.

В выражениях (10)–(11) введены следующие обозначения:

то

-A P ; = T f (I ^r , ; ^{- 5 -}n ^A| ) ^exP ⁽ i qrj ⁽¹²⁾ j = 1, ^j *

– решеточная сумма, описывающая поле, создаваемое наночастицами ; -го слоя в центре принадлежащей ему i-й частицы; r,; - радиус-вектор j-й частицы ; -го слоя, то

C ^ ; ( ( ; ^{- к} ) ^A ) = T ^f< (1 ^{5 +}n ^{A - r} ,к I) ^e xp ( ¹ ч^ к ) .(13) , = 1

– решеточная сумма, описывающая поле, создаваемое к- м слоем в i- й частице ; -го слоя. При этом C p имеет место при к > ; (поле излучается в положительном направлении оси z , аргумент C ³ р ; ( ( ; - к ) A ) - положительный вектор), а C_p - при к < ; (поле излучается в отрицательном направлении оси z , аргумент C ³ ; ( ( ; - к ) A ) -отрицательный вектор). Вычисление решеточных сумм вида (12) и (13) проделано нами ранее [14–16] и здесь приводиться не будет. Отметим, что учет ненулевых затухающих гармоник в сумме С р необходим лишь в случае больших значений постоянных решетки, малых радиусов частиц либо больших длин волн [14–16], поэтому можно записать следующее выражение для C p :

^<С р ( r ) = ^C n ^e xP ( + ^{1 k} 0 r i^ m ) ^,