Наноразмерные эффекты в полевой эмиссии электронов ультратонкими металлическими плёнками

В последние годы достигнут существенный прогресс в экспериментальном изучении полевой эмиссии электронов наноразмерными структурами, такими как наноуглеродные трубки, наноразмерные нити, нано-кристаллические плёнки и другими [1, 2]. Исследования показали, что наиболее эффективную полевую эмиссию представляют наноструктурированные материалы. Центрами эмиссии в наноструктурах являются наноразмерные проводящие образования, окружённые изолирующей фазой (как, например, в нанокристалли-ческих алмазных плёнках) или вакуумом (ориентированные нанотрубки, нанонити). Обнаружено также, что для эмиттеров на основе углеродных соединений достигаются рекордно низкие значения для электрического поля, вызывающего эмиссию электронов. Экспериментально доказано, что существенную роль в повышении эмиссионной способности наноструктур играют квантово-размерные эффекты, которые приводят к снижению работы выхода из наноразмерных образований [3, 4, 5, 6]. Другой наблюдаемый эффект связан с сужением энергетического спектра эмитированных электронов при уменьшении характеристических размеров структурных элементов и, тем самым, с увеличением длины когерентности эмитированных электронов [7]. Представляется очевидным, что для теоретического описания наблюдаемых наноразмер-ных эффектов необходимо последовательное квантово-механическое рассмотрение процесса полевой эмиссии электронов, т.е. эмиссия должна рассматриваться как туннельный переход между двумя многочастичными электронными квантовыми состояниями, энергетическая структура которых явно зависит от размеров эмиттера и коллектора. Такую возможность даёт метод гамильтониана переноса, предложенный Бардиным [8] и развитый в ряде более поздних работ [10, 9, 11], в основе которого лежит квазиклассическое приближение квантовой механики.

След ует отметить, что существуют и друг ие теоретические подходы для описания квантовых зако-номерностtq полевой эмиссии электронов: форма- лизм квантовой теории рассеяния на "embedding" потенциалах [12]; метод прямого интегрирования, зависящего от времени уравнения Шредингера в приближении локального функционала плотности [13, 14, 15]; метод классического статистического туннелирования [16]. Все перечисленные подходы так или иначе учитывают не только квантов ую природу самого эффекта туннелирования, но и квантовые эффекты в начальном и конечном состоянии. Однако в подходе Бардина [8] эмиссионный ток выражается через волновые функции электрона из катода и анода в подбарьерной области, которые получены независимо друг от друга с учётом приложенного электрического поля, но нормированы на волновые функции невозмущ ённой задачи. В этом случае не нужно решать трудную, требующую дополнительных предположений и знания полного гамильтониана задач у о нахождении волновой функции электрона во всём пространстве.

1. Метод Бардина

Метод Бардина основан на квазиклассическом приближении квантовой механики Вентцеля-Крамерса-Брюллюэна (ВКБ) [17] и позволяет решить задачу о квантовом туннелировании, не решая уравнение Шредингера для тунн елирующей частицы в области туннельного перехода. Туннельный ток квантового перехода может быть получен из золотого правила Ферми [18] и представляется в виде:

I=4πq∑|ML,R|2 δ(ER-EL), (1) ℏ L,R где q – заряд электрона, ℏ – постоянная Планка, символы L и R отвечают, соответственно, квантовому состоянию электронов в катоде (эмиттере) и аноде, дельта-функция Дирака δ(ER - EL ) отражает закон сохранения энергии в процессе квантового туннелирования, ∑L,R – означает суммирование или интегрирование по начальным и конечным состояниям эмиссионных электронов. ML,R – амплитуда квантового перехода электрона из катода в анод, связанная с соответствующим током перехода, записывается в виде двухкратного интеграла по поверхности YZ перпендикулярной направлению эмиссии X :

M L , R =      J -^d У ^d z ^{[ T} L ⁽ x, У, z ) y-^ R ⁽ x, У, z ) ^-

■     2 m^JJx = ^x                   d x

∂

-TR(x■ y■ z)— TL(x■ y■ z)], x = x - поверхность в области, запрещённой для классического движения, условия фиксирования которой будут рассмотрены позже. TR (x, y, z) и TL (x, y, z) - волновые функции электрона из анода и из катода в области подбарьерного перехода. Поскольку электрическое поле приложено нормально к поверхности катода и Гамильтониан электронов распадается на сумму двух частей, зависящих только от x или только от y и z , то зависимость от координат в волновых функциях электронов факторизуется

^T L , R ⁽ x ■ У ■ z ) = F L , R ⁽ x ^{) Ф} L , R ⁽ У ■ z )•

Обычно область эмиссии электронов в плоскости YZ считается достаточно большой по сравнению с де Бройлевской длиной волны электронов и для описания поперечного квазисвободного движения электронов используется приближение плоских волн, при котором волновые функции электрона могут быть записаны в виде:

i ( k^L • ^Ry + k^L • ^Rz ) Ф L , R ( y , z ) = e ^y z

.

В этом случае в формуле для амплитуды перехода M _LR (2) можно выполнить интегрирование по y и z ,

^Ф L , R ⁽ У , z ^)d У ^d z = ⁸ L r ⁸ , L ,R ,

J J ,                              k , k k , k

У , У z , z что даёт

Й2    . й

Ml r =--[ F :( x )— F ( x )

L , R        L L \ / Rx/

2 m      d x

-

^F R ⁽ x ) Э X ^F L ⁽ x^ kL • kR ⁸ kL • kR . О x             y , y z , z

Представим сумму (интеграл) по начальным и конечным квантовым состояниям следующим образом:

I = III,

L>R Lx ,RxkL ,kRkL ,kR x x У , У z , z тогда из (1) и (2) получаем

I = 4nq I I lf"[F*(x)TFr(x)-й l ,r ,l r, 2m        dx x , xky ,k z

-Fr(x)d-FLXx)] |x=x 8(eL -eR)f (El)(1 - f (Er)), ∂x где f (Elr ) - функция распределения Ферми по квантовым состояниям,

^£ L , R    ^E L , R

-

E L , R

• -    энергия, связанная с движением по оси X , и й²

< R = — (( k L ’ ^R ) ² + ( k L ’ ^R ) ² )

2 m

• -    энергия движения в плоскости YZ .

В квазиклассическом приближении [19] волновые фун кции электронов в подбарьерной области, запрещ ённой для классического движения, представляются в виде:

C x

FL,R (x) = —Г" 1 KL,R 1    eXP (aL,R J    1 KL,R 1 dx),     (4)

2                             xxR, R где aL = -1, aR = +1 и

^K l , r =J^^r^(ue!f ^{( x} ) ^- qE ^{x -e} l , r ), V й

E - приложенное электрическое поле, x_LR - левая (со стороны катода) и правая (со стороны анода) границы области, запрещённой для классического движения, U ef ( x ) - эффективная высота потенциального барьера межд у катодом и анодом при приложенном поле. Например, в случае плоского металлического катода, с учётом сил электростатического изображения, можно записать:

u ef ( x ) = E f +_ф- q ² ,

4x где Ef - энергия Ферми электронов в катоде, ф -работа выхода электрона из катода.

В традиционной постановке задачи о полевой эмиссии электронов полагают, что квантовый переход осуществляется в состояния непрерывного спектра или в вакуум. При этом учитывается, что электроны достигли анода, а какие они заняли при этом квантовые состояния - безразлично, т.к. измеряется только анодный ток, который является интегралом по всем состояниям. В этом случае полагают, что все состояния справа от барьера свободные, т.е. f ( E_r ) = 0, а нормировочная константа C_R может быть выражена через энергетическую плотность квантовых состояний непрерывного спектра р _R ( е _R ):

C =1    ² m

^{R Й}\ ^ПР R ^{( е} R )

.

От суммирования по конечным состояниям надо перейти к интегрированию по правилу:

I ^ JdeRРR (еR).

R _x

Нормировочная константа C L определяется из условия сшивания невозмущённой (при нулевом приложенном поле) волновой функ ции электрона из катода Ф _L ( x ) и волновой функции в подбарьерной области F L ( x ) (4) в некоторой точке x'_L , за которую можно выбрать координату точки достаточно близкой к x_L . Таким образом:

Cl = 2ФL (xL )(-;Г) | Uf (xL) - qExL - еl |1/4 й exp(JxL | Кl | dx).

x _L

После подстановки волновых функций (4) в (3) получаем

I'т 22 (К)(CL) ℏ L L L 2m 4π k ,k x y, z

exp( - 2 j" к _L\dx ) f ( E l ).

x _L

Если слева от барьера (в катоде) движение по осям Y и Z можно рассматривать как квазисво-бодное, то суммирование по дискретным квантовым состояниям можно заменить интегрированием по непрерывному сп ектру волновых чисел k_y ^L и k_z ^L :

k Ъ = ^2^{Jd k} ' ^{Jd k} z ^{f (} E L )= y ^, z

= T" I (^r)(kBT)ln( 1+exP 4п К

σ

4π

v

EF -

к T

BT J J

,

где σ – площадь поверхности, с которой осуществляется эмиссия электронов, k_F ² = 2 mE_F / ℏ² ,

заны только с одним направлением, которое совпа-даёт с направлением эмиссии электронов. Рассмотрим в рамках подхода Бардина полевую эмиссию электронов ультратонкими металлическими плёнками. В этом случае нам необходимо вернуться к формуле (7), в которой необходимо учесть, что эмиссия электронов происходит с некоторых дискретных уровней, возникших за счёт локализации движения по оси X . Т.е. движение электронов в плоскости YZ будем, как и раньше, считать квазисвободным и, следовательно, распределение электронов по энергетическим уровням подчиняется закону Ферми с граничной энергией E_F . В то же время, по оси X движение электронов ограничено размерами плёнки и его можно в первом приближении моделировать как движение в потенциальной яме конечной глубины и конечного размера. В этом случае из (7) для плотности эмиссионного тока получаем следующую формулу:

k_B – постоянная Больцмана, T

абсолютная

температура.

С учётом (5) и (6) плотность эмиссионного тока равна:

I

σ

= -^2 2^{( k}B^{T )ln 1} + exp 4 π ℏ L   ^B

x

v

EF—E, )' квТ JJ

×

x C L exp I - 2 J R | к _L | d x I .

V XxL          J

В приближении квазисвободного движения электронов по оси X , когда размер катода в направлении эмиссии много больше де Бройлевской длины волны электрона, в (3) надо положить, что

_C = 1    2 m

^L ℏ πρ _L ( ε _L )

и

2 ^ Jd£LP L (£L ).

L _x

Тогда эмиссионный ток записывается в виде, из которого может быть получена хорошо известная формула Фаулера-Нордгейма [20], отвечающая случаю вырожденного электронного газа ( T = 0) :

FN qmk_BT

2 π ² ℏ ³

∞

J o ln 1 +

V

Ef-^^ )' квТ JJ

×

I xR                   I x exp I -21   | кL | dx I deL.

V     ^XxL            )

2. Модель

В экспериментальных работах [3, 4, 5, 6] было показано, что размерные эффекты начинают играть роль, когда характеристические размеры нанообъектов становятся около 10 нм. Так, в работе [5] исследовались характеристики проводящих углеродных наночастиц толщиной 3-40 нм, синтезированных на поверхности алмазоподобной плёнки, а в работе [6] изучалась зависимость работы выхода электронов от толщины ультратонкой графитовой плёнки (7-25 нм). Во втором случае наноразмерные эффекты свя-

J = qk B T 2 ^C » ^еХ Р ^{( -}Ч xR ^, n ^{1 K} L , n ^{( x} ) ¹ d x ) ^x 4 π ℏ _n               ^xL , n

I

× ln 1 + exp

V

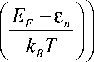
где

C_n ≃2 Φ _n ( x_L ′ ) κ _L ( x_L ′ )exp( ^{xL ′} | κ _L |d x ),         (10)

x _L

Φ _L ( x ′ _L ) – невозмущённая волновая функция электрона в точке близкой к границе раздела плёнка-ва-куум, n – нумерует квантовые состояния дискретного спектра в одномерной потенциальной яме по оси X .

Для численной оценки б удем полагать, что потенциальная яма имеет левую бесконечно высокую стенку при x = - a , за нулевой отсчёт энергии выберем значение потенциальной энергии на дне ямы, правая стенка ямы имеет координату x = 0 и высоту U = E_F + ϕ , порядка нескольких электрон-вольт. При выбранн ой геометрии задачи ( см. рис. 1)

2 m     q ²

κ _L ( x )=     ( U -   - qEx -ε _n )

ℏ ²       4 x

и

x L , R

U -ε n ± ( U -ε n ) - q ³ E 2 qE

Решение стандартного одномерного уравнения Шредингера для электрона в потенциальной яме конечной глубины U даёт условие квантования для безразмерной переменной ξ :

sin( ξ n ) _{= ±} 1

,

VC

n

где

C = 2 mUa ² / ℏ ² , ξ _n = k_na , η ² n = C -ξ ² n , ε n = U ξ ² / C .

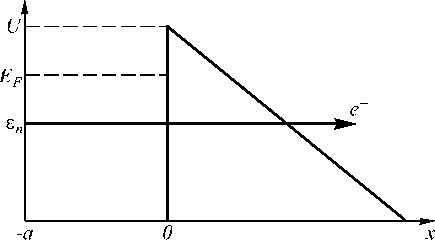
Рис.1. Форма потенциального барьера при приложенном электрическом поле

эффектов не возникает и плотность тока, в случае непрерывного спектра по энергиям, вычисляется по формуле

FN

× exp

Квадрат модуля нормированной волновой функ-

ции в точке x = x_L ′ > 0 равен

| Φ n ( x ′ L )| ² = 1 a

² ^ n ⁿ n   | e -2л _n xL / a

. C (1 +n n ) ^J

3. Численные оценки

Для упрощения численной оценки рассматриваемых эффектов не будем учитывать силы электростатического изображения, при этом инт еграл в экспоненте, определяющей вероятность туннелирования, может быть вычислен в элементарных функциях [19]. В этом приближении

U ^eff ( x )= U = E_F +ϕ ,

κ _L ( x )= 2 m ₂ ( U - qEx -ε _n ), ℏ ²

x_L = 0,   x_R

U -ε

n

qE

Также можно положить, что x_L ′ = x_L = 0 . Расчёт-

ная формула для плотности эмиссионного тока с n -го квантового уровня, зависящая от толщины плёнки и глубины потенциальной ямы по направлению

перпендикулярному поверхности эмиссии, пред-

ставляется в виде

= qk _B T n π _ℏ

I Ф n (0) | ² К L (0)ln 1 + exp

V

E _D £ | "tr n J ^л BT ) J

×

× exp

( 4 1 2 m

V^— 3N ~E

( U - ε n ) ^3/2 eE

Число дискретных энергетических уровней в зависимости от толщины плёнки a можно оценить

n ⁽ a ) = J p l ^{( £ )} d E =

a 2 mE_F

π ℏ ²

I a I

= 4,3----- I .

I 1 нм J

Критерием перехода от дискретного спектра к непрерывному распределению по энергиям может быть малость отношения среднего расстояния между уровнями к ширине энергетической зоны

δ ( a ) =

∆ε = 1

E_F n ( a )

= 0,23 | 1 нм I .

V a )

Можно ожидать, что уже при толщин е плёнки около a ≃ 100 нм или больше квантоворазмерных

qmk_BT 2 π ² ℏ ³

.    I j de In 1 + exp

.0       V

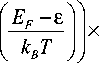
Для холодных катодов ( T ≃ 300 K, k_BT = 2,6 ⋅ 10 ^{- 2} эВ) плотность заселения энергетических уровней выше энергии Ферми E_F ничтожно мала, а э кспо-ненциальный множитель в (13) и (14) быстро убывает, когда разность E_F - ε растёт. Поэтому в арг у-

менте экспоненты можно приближенно записать

( U - ε ) ^3/2 ≃ ϕ ^3/2 + 32 ϕ ( E_F -ε ).

С другой стороны,

при низких температурах фактор, учитывающий заселённость уровней, также упрощается

I kBT In 1 + exp

V

EF-e )' квТ JJ

≃ E F

-ε

и в (14) интегрирование по энергиям электронов выполняется элементарно. В силу быстрой сходимости, верхний предел в интеграле может быть положен бесконечно большим, что даёт

-fn    q ³ E ²      Г 4 2m ф ³/²

=^^exp V ^—1V 1ё "EE J

Поскольку для ультратонких плёнок спектр энергетических состояний надо считать дискретным, то разностью E_F - ε _n для конкретного уровня

нельзя пренебречь и формула для эмиссионного тока (13), с учётом (12), записывается в виде

J = q    2ξnηn (E -ε )× n 2         Fn лйa VC(1 +nn))

× exp

I 4 1 2 m

V—Jv "йГ

( U - ε n ) ^3/2 qE

Можно показать, что в пределе a → ∞ или C → ∞ уравнение на собственные значения (11)

упрощается: sin( ξ _n )=0,

ε n = ε 1 n ² ,

ξ _n = k_na = π n ,

22 π ² ℏ ²

ε ₁ =         .

2 ma ²

В предположении, что эмиссия идёт только с одного самого близкого к энергии Ферми E_F уровня,

получаем a→∞ Jn

q ³ E ²      Г 4 2m ф ³/²

ЕЕйф ^exp V^—33 IE "EE J

что достаточно хорошо согласуется с (15), т.к. 2 e π ³ ≃ 168, 5 , а 16 π ² ≃ 157, 9 . Для численных оценок

рассмотрим медную плёнку, для которой: E F = 7 эВ, ф = 4,5 эВ, U = 11,5 эВ. Заметим, что выбранные численные значения получены в экспериментах с макроскопическими образцами и вопрос о прямом измерении работы выхода электронов с ультратонкой плёнки остаётся открытым.

На рис. 2 показана рассчитанная нами зависимость от толщины плёнки отношения

R ( a , qE )= £ J_tt / J ^FN

n при приложенном поле qE = 1 эВ/нм.

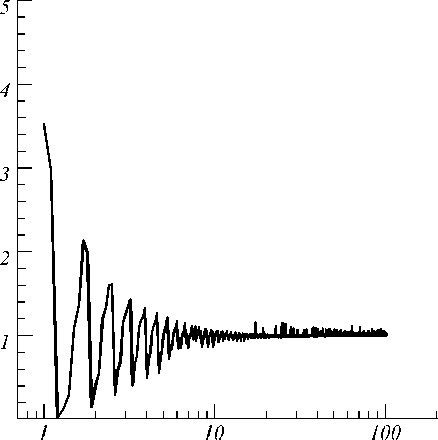
Рис. 2. R(a,qE ) в зависимости от a (нм) при qE = 1 (В/нм)

Заметим, что для толщин плёнки a<10 нм эмиссия происходит только с самого верхнего уровня, наиболее близкого к EF, а вклад остальных уровней сильно (на порядок и более) подавлен. В случае более толстых плёнок уже необходимо учитывать соизмеримые между собой вклады нескольких верхних уровней. Таким образом, качественным эффектом, подтверждающим наноразмерные эффекты в полевой эмиссии электронов ультратонкими плёнками, было бы наблюдение пиков в энергетическом спектре электронов. Число пиков зависит от толщины плёнки и приложенного поля: чем меньше a, тем меньше пиков. С увеличением приложенного поля число уровней, дающих вклад в эмиссионный ток, также увеличивается пропорционально E2. Однако это заметно только для достаточно толстых плёнок с a>30 нм, когда полное число энергетических уровней становится достаточно большим. Рис. 2 показывает, что отношение R(a, qE) при qE = 1 эВ/нм имеет ярко выраженную структуру дискретных пиков, когда толщина плёнки становится меньше, чем a<10 нм. Наблюдаемое поведение является проявлением квантового характера движения электронов в направлении перпендикулярном поверхности ультратонкой плёнки. Уменьшение отношения практически до нуля при некоторых значениях толщи- ны a связано с тем, что при выбранных параметрах (a, U) энергия самого верхнего заселённого уровня значительно меньше энергии Ферми EF и эмиссия с него сильно подавлена фактором, определяющим вероятность туннелирования через барьер. В модели предсказывается также и существование дискретных уровней с энергией больше, чем EF. Однако вероятность их заселения при T — 300 K ничтожно мала и вклада в эмиссионный ток они не дают.

Если уменьшать приложенное поле до значений, при которых наблюдается эмиссионный ток в наноструктурах из графита, примерно qE = 0,01 В/нм, то величина тока, вычисленная по формулам (15) и (16), экспоненциально падает до пренебрежимо малых величин. Причём вклад дискретных уровней падает быстрее и ст ановится меньше, чем значения, рассчитанны е по формуле (15), как это видно на рис. 3. Это объясняется тем, что с уменьшением приложенного поля сужается область энергий электронов, дающих вклад в эмиссию и в том случае, когда эмиссия идёт с одного или нескольких дискретных уровней, значения энергий этих уровней оказывается значительно меньше, чем E_F .

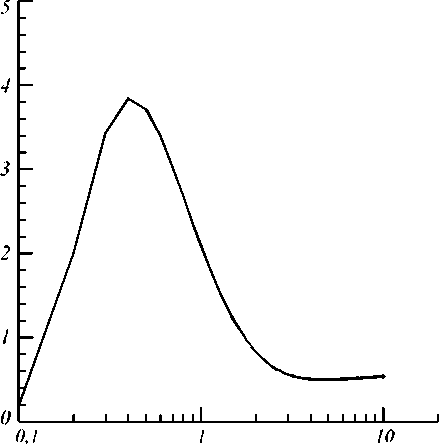
Рис. 3. R(a,qE ) в зависимости от qE (В/нм) при a = 1 нм

Для объяснения экспериментально наблюдаемых эмиссионных токов при низких приложенных полях обычно делают предположение, что с уменьшением размера эмиттера хотя бы по одному направлению до уровня нанометров уменьшается работа выхода электронов с поверхности эмиттера. Такие предположения основываются на гипотезе, что для описания эмиссионных токов из ультратонких плёнок может применяться формула Фаулера-Нордгейма (15), в которой, формально уменьшая работу выхода ф до значений в 10-2 ^10-3 эВ, можно описать экспериментальные данные. Однако, как показывает даже качественный анализ, дискретный характер спектра энергий наноструктур приводит к другому типу зависимости эмисси- онного тока от приложенного поля, который не описывается простой непрерывной зависимостью (15).

Заключение

В работе получены след ующие результаты:

• -    в модели прямоугольной потенциальной ямы получена формула для расчёта эмиссионного тока электронов ультратонкой металлической плёнкой с учётом дискретной структуры энергетического спектра (16),

• -    проанализирована зависимость величины эмиссионного тока от толщины плёнки и приложенного электрического поля,

• -    показано, что для тонких плёнок и слабых полей формула Фаулера—Нордгейма (15) не может описать дискретный характер зависимости эмиссионного тока, связанной с наноразмерными эффектами, при любом выборе параметров модели.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант РФФИ 10-07-00453. Автор благодарен Д.Л. Голо-вашкину и В .Д. Фролову за интерес к работе и полезные обсуждения полученных результатов.