Напорная теория несущего винта вертолета

Введение. Впервые предположение о подобии аэродинамических характеристик лопасти несущего винта (НВ) вертолета и крыла самолета было высказано С.К. Джевецким в 1892 г. [1]. Это позволило предположить, что на лопасти винта и крыле возникают сходные аэродинамические силы, а это значит, что к воздушному винту можно применить теорию подъемной силы, разработанную для крыла Н.Е. Жуковским совместно с С.А. Чаплыгиным. Над решением этой проблемы в начале двадцатого столетия работали Н.Е. Жуковский, Б.Н. Юрьев, Г.Х. Сабинин. Однако в то время сделать этого не удалось. В настоящей работе сделана попытка решить эту задачу.

Основные положения напорной теории. Для определения подъемной силы крыла самолета вычислим скоростной напор pV2

qk = ^, где V - скорость полета самолета; p - плотность воздуха на расчетной высоте.

Определим скоростной напор для винта вертолета

(0 5 U )²

qB =Р , 2кл , где Uкл – окружная скорость конца лопасти вертолета.

Получим подъемную силу крыла самолета

Y = C — S, y2

где С у – коэффициент подъемной силы крыла самолета; S – площадь крыла самолета.

Вычислим тягу несущего винта вертолета

• p, = r о (-, кл ). p

• ^г НВ ^Y .ср ^р       2       'л ,

где C_{y .ср} – среднее значение коэффициента подъемной силы комлевого и концевого сечений лопасти несущего винта (НВ) вертолета (определяется по таблице аэродинамических профилей

С   + Су

• [3]    и имеет вид C y _ср = у ™^мл ^ у™™ ); Л _л - суммарная площадь оперенной части лопастей

вертолета

F л = L о^л Вz , где L _о.ч.л – длина оперенной части лопасти; B – хорда лопасти; z – число лопастей.

Зависимости (1) – (4) подтверждают предположение С.К. Джевецкого о подобии аэродинамических характеристик лопасти несущего винта вертолета и крыла самолета.

В основе разработанной напорной теории воздушного винта (НТВВ), и в частности НВ вертолета, лежит определение скоростного напора на оперенной части лопасти (2), а также геометрических параметров лопасти НВ.

Тогда выражение (4) можно представить:

0 5 U ² р =с о ^-,__— L Bz

• Р НВ ^иу .ср ^р      2      L Q4^ ^BZ .

Для определения реактивного момента (РМ) НВ воспользуемся формулой:

M p = С_х ._ф ^{p (} 0' ^ ) F_nR ,

где C_{х .ср} – средний коэффициент лобового сопротивления лопасти, C_{х .ср} деляется по таблице аэродинамических профилей [3]; R – радиус НВ.

Определим расчетную мощность двигателя

N u = ^0,5^,

^ х .компл + ^ х .компл

, опре-

а также реальную мощность двигателя

N p = N u G n ,                                        (8)

N где GN - весовой коэффициент мощностной безопасности, введен автором, GN = — .

N                                                                   N _{N U}

Определим скорость индуктивного потока воздуха в плоскости вращения НВ

U С _

I/ = ^w кл^ у .ср

¹ п ,

где п - коэффициент загрузки НВ, величина обратная коэффициенту заполнения ° ,

P / F

П _ нв * л

НВ / НВ

, где F _HВ = n R² - площадь ометаемой поверхности НВ.

Тогда

V,=UoC .                               (10)

/ 1       кл ^ у .ср .

Скорость индуктивного потока на расстоянии (1,5–2) R [4] от НВ

V / 2 _ 2 V -                                               (12)

С помощью НТВВ была определена очень важная зависимость между весовым расходом воздуха для заданного НВ и его тягой. Эта зависимость названа автором коэффициентом приемистости тяги винта Z t , размерность – секунда, с.

Z

0 _ ^v m

t

НВ

где © _m - весовой расход воздуха НВ на заданной высоте: © m ©v Y ,

где © V - объемный расход воздуха на заданной высоте, © V = F _HB V -2 ; у - удельный вес воздуха на заданной высоте.

Коэффициент приемистости тяги Z t зависит от весового расхода воздуха на расчетной высоте и имеет тенденцию к уменьшению с увеличением нагрузки на НВ при F НВ = const, т. е. если НВ         НВ

I FI > I FI , то Z t1 >  Z t 2 .

V F HB )1 v F HB Л

Используя Z t , определим расчетную мощность двигателя

где ° - коэффициент заполнения НВ реактивного момента НВ, а = F ¹⁵-.

F л

Тогда реактивный момент

M P = C х .ср^(0,5 Vⁱ ₂ ^{1 / σ ) 2} F л R .                                   (16)

Тяга несущего винта

(0, 5 V_{i 1} / σ )²

Р _НВ = C_{y .ср} ρ       2       F _л .                                    (17)

В табл. 1 представлены значения коэффициента тяги для различных скоростей индуктивного потока V_{i 2} и различных значений диаметров НВ для вертолетов Ми-2, Ми-24, Ми-26.

Таблица 1

Значения коэффициента приемистости тяги Z t , с

Vi 2 , м/с	Диаметр несущего винта, м
	14,5 (Ми-2)	17,4 (Ми-24)	32 (Ми-26)
19	1,1
38,4		1,0
42,2			0,8

Напорная теория воздушных винтов позволяет с помощью коэффициента приемистости тяги Z t и скорости индуктивного потока определить основные характеристики несущего винта:

• –    объемный расход воздуха Θ V ;

• –    весовой расход воздуха Θ m ;

• –    тягу двигателя Р НВ ;

• –    реактивный момент винта M р ;

• –    расчетную мощность двигателя N U .

Алгоритм определения основных характеристик несущего винта вертолета.

• 1.    Зададим радиус несущего винта R и скорость индуктивного потока V_{i 2} .

• 2.    Определим:

• –    площадь ометаемой поверхности F _НВ = π R ² , м²;

• –    объемный расход воздуха Θ _V = F _НВ V_{i 2} , м³/с;

• –    весовой расход воздуха Θ _m = F _НВ V_{i 2} γ , кН/с;

• –    коэффициент приемистости Z t (табл. 1);

• –    тягу НВ P = ^{Θ m} , кН;

НВ           ,

Zt

Θ 0,5 V

• –    расчетную мощность двигателя N = ^{m    i 2} , кВт;

^{U    Z}t   ^σ

• –    по атласу аэродинамических характеристик крыльевых профилей средний коэффициент лобового сопротивления лопасти [3] C_{х .ср} ;

(0,5 V / σ )²

• –    реактивный момент M _P = C_{х .ср}      ^{i 1}      F _л R , кН·м.

Достоверность напорной теории воздушных винтов была проверена на специально выполненной экспериментальной установке (ЭУ) (см. рисунок).

Кроме этого было проведено исследование статистических данных вертолетов, имеющих взлетный вес от 3,5 т до 56 т (Ми-2, Ми-24, Ми-26).

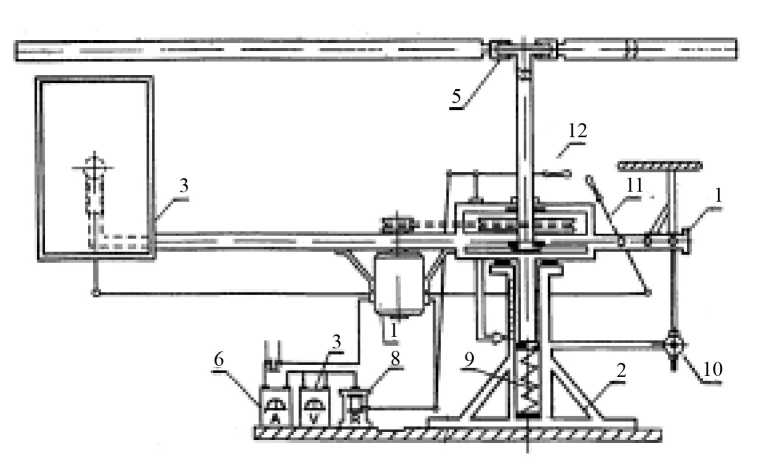
Экспериментальная установка по определению потребной мощности двигателя, силы тяги и реактивного момента:

• 1    – подвижная часть установки; 2 – неподвижная часть установки; 3 – стабилизатор для парирования реактивного момента НВ; 4 – электродвигатель ( N ном = 4,3 кВт); 5 – несущий винт ( d = 3,7 м); 6, 7 – амперметр и вольтметр для замера потребной мощности двигателя; 8 – реостат для регулировки мощности двигателя; 9 – оттарированная пружина для замера тяги несущего винта; 10 – динамометр для замера реактивного момента несущего винта; 11 – ручка управления стабилизатором;

• 12 – ручка управления электродвигателем

Данные исследования приведены в табл. 2. Среднестатистическая погрешность между замеренными и расчетными данными не превышает погрешности измерений.

Таблица 2

Статистические и экспериментальные данные НВ и ЭУ

Тип вертолета и ЭУ	Параметры НВ	Статистические данные вертолетов и замеренные параметры ЭУ	Расчетные данные (по НТВВ)	Погрешность параметра, %
ЭУ σ = 0,06	n = 6,5 об/с	Р = 1,40 кН	Р = 1,39 кН	0,99
	R = 1,85 м	М р = 1,25 кН·м	М р = 1,23 кН·м	0,98
	L = 1,6 м	N п.д = 6,5 кВт	N п.д. = 6,5 кВт	0
	в= 0,16 м, Z =3	V i 2 = 13 м/с	V i 2 = 12,5 м/с	0,96
Ми-2 σ = 0,06	n = 3,1 об/с	Р = 35,0 кН	Р = 34,1 кН	0,97
	R = 7,25 м	М р = 16,0 кН·м	М р = 16,3 кН·м	0,98
	L = 6,4 м	N п.д. =2·350 л.с. = 514,2 кВт	N п.д = 352 кВт	–
	в= 0,41 м, Z =3	Vi 2 = 19,0 м/с	Vi 2 = 18,7 м/с	0,95
Ми-24 σ = 0,06	n = 4,0 об/с	Р = 115,0 кН	Р = 113,0 кН	0,98
	R = 8,6 м	М р = 105,0 кН·м	М р = 107,0 кН·м	0,98
	L = 7,2 м	N п.д = 2·2200 л.с. = 3235 кВт	N п.д = 1480 кВт	0,9
	в= 0,58 м, Z =5	Vi 2 = 38,0 м/с	Vi 2 = 38,8 м/с	0,97
Ми-26 σ = 0,06	n = 2,1 об/с	Р = 560,0 кН	Р = 556,95 кН	0,99
	R = 16,0 м	М р = 750,0 кН·м	М р = 752,0 кН·м	0,99
	L = 13,3 м	N п.д = 2·11500 л.с. = 16911 кВт	N п.д = 8500 кВт	0,99
	в= 0,8 м, Z = 8	Vi 2 = 42 м/с	Vi 2 = 42,2 м/с	0,97

Выводы.

• 1.    Из формул (4), (5), (8), (9) следует, что в основе напорной теории воздушных винтов лежит скоростной напор, подобный скоростному напору крыла.

• 2.    Параметр 0,5 U _кл является основным в напорной теории воздушного винта и заменяет параметр скорости полета самолета в скоростном напоре крыла.

• 3.    Сравнение основных характеристик, полученных на ЭУ, с расчетными и статистическими данными вертолетов Ми-2, Ми-24, Ми-26 (табл. 2) свидетельствует, что разница в значениях не превышает погрешности измерений.

• 4.    На основании предложенной напорной теории воздушных винтов можно разработать простой и достаточно точный метод определения основных характеристик воздушных винтов.